基于LANDMARC的室内定位算法改进
彭慧珺,时宗胜,孙知信
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏中天科技软件技术有限公司,江苏 南通 226000)
0 引 言
随着无线通信技术的迅速发展,人们对物品位置信息的需求越来越多,室内定位技术[1]受到了广泛关注。室内定位技术可应用于医疗、工业、商业、军事管理或跟踪系统中,如医院中对医生病人、器械的调配,图书馆中重要图书的位置信息,特别是危急时刻对目标的定位能大大增加救援效率,减少伤亡和财物损失,具有非常广阔的应用前景。
针对不同的室内环境,涌现出了各种各样的室内定位技术。WiFi技术[2]以普遍的WIFI系统为核心,是一项造价成本低廉且非常易于实现的定位技术。Zigbee技术[3]则是一种可靠性高、功耗低的自组网,它的定位方式主要是依靠距离与接收信号强度之间的关系,但成本相对较高且缺乏扩展性。射频识别技术(RFID)[4]采用射频方式进行非接触双向无线通信,特点是成本较低却具有较高的抗干扰能力和强大的穿透性。超带宽技术(UWB)[5]的优点是实时性高,有较高的安全性,穿透能力强,但与此同时成本也比其他技术要高。蓝牙技术[6]应用于小范围定位,其器械小功耗低,且信号传输不受视距的限制,但较差的抗干扰能力使得定位不够精准。
文中研究的LANDMARC[7]是RFID室内定位的典型算法,以其低廉的运行成本和较高的抗环境干扰能力,成为应用最为广泛的定位算法之一,因此对LANDMARC算法定位精度与稳定性的提高进行研究,具有重要的研究价值和应用前景。
1 相关技术研究

文献[12]创造性地提出了一种归一化权重的方法,将与一个RSS值成比例的加权因子添加到关联度计算的方程中,能够更精确地反映出参考标签与目标标签的位置关系,这种定位方法减小了定位系统的最小误差,但对目标定位的平均误差没有明显改善;同时文献[12]还提出了另外一种解决方法,称为放弃最近阅读器,即排除距离目标标签最近的阅读器所读信号强度值,可以有效防止可能大误差的产生,最后该文献将两种方法相结合,得到归一化权重的放弃最近阅读器法,提高了算法的定位精度,且在一定程度上降低了大误差的发生可能性。该算法虽改善了定位精度,但未从根本上解决算法定位过程中的漏洞,稳定性不高。
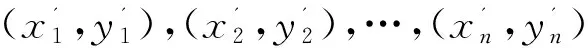
上述文献均是对LANDMARC室内定位算法定位过程的改进,这些改进方法能够在一定程度上减小误差,提高定位精度。但这些算法仍存在以下两点不足:
(1)受多径效应[17]的影响,信号强度值读取易产生偏差,导致LANDMARC算法对目标的坐标计算出现误差,需要进行修正。例如文献[8]虽修正了目标位置的计算误差,但三角定位法计算的误差值不能准确反映出对目标位置计算的偏差值,因此目标位置的修正上仍有改进空间。
(2)LANDMARC算法的定位过程存在不稳定因素。由于RFID阅读器读取的是信号强度能级,具有离散性,当参考标签与目标位置极近时,两者关联度值为零,造成在权重计算中产生异常值,导致定位过程发生紊乱,而鲜有文献针对算法的稳定性进行改进。
文中针对LANDMARC算法的不足进行分析,在LANDMARC定位过程中引入自修复机制,该机制分为关联度修复和坐标修复两个过程,对关联度异常值与坐标偏差值进行修正,有效提高了算法精度和稳定性,使LANDMARC算法具有自我修复能力。
2 改进的LANDMARC算法
2.1 自修复机制
2.1.1 关联度修复
RFID阅读器在LANDMARC系统中读取值是接收信号强度的能量等级值,具有离散性。即使现代RFID阅读器拥有较高的能量等级数目,也无法避免当参考标签与目标位置靠得极近时,在阅读器中所读取的信号强度等级值相同的情况。当发生这一情况时,会造成参考标签与目标之间的关联度e为零,权重公式极限为1,使定位过程发生紊乱,即
(1)
为了避免发生该情况,需要对LANDMARC算法定位过程进行优化,在定位过程中随时检测参考标签与目标的关联度值,也就是自修复机制的第一阶段关联度修复。关联度修复过程引入修复值α,当发现存在与目标关联度值为零的参考标签时,用修复值α对异常的关联度值进行替换,其取值为:
(2)
其中,Emin是所有参考标签与该目标的关联度中非零关联度的最小值,将修复值取为最小非零关联度值的一半,这样既能够保证所有参考标签与目标的关联度中没有零值,也能使修复后的关联度值仍然是所有参考标签与目标关联度中最小的。关联度值越小说明参考标签距离目标越近,保留了关联度为零值的参考标签原有的特性。
自修复机制的关联度修复过程如下:在关联度修复的初始阶段,首先从关联度矩阵中检测是否存在零值的关联度。若不存在,则直接跳过该修复过程,继续进行对目标的定位;若存在这样的关联度,自修复机制将遍历参考标签与目标的关联度矩阵,获得最小的非零关联度值Emin,从而生成修复值α,并对该异常的零值关联度值进行替换。当该参考标签关联度修复完成后,继续进行异常关联度值的检测判断,若不再存在零值关联度,则跳转下一阶段,继续进行目标定位;否则使用上一回合生成的修复值α,对该参考标签异常关联度进行修复。当替换结束后,继续进行关联度异常值的判别检测,直到所有参考标签与该目标的关联度值全部修复为非零值为止。
2.1.2 坐标修复
受到电磁波的反射、折射以及多径效应等不良因素的影响,参考标签信号强度RSSI值发生偏差,将造成不小的定位坐标误差。为了提高定位精度,减轻干扰因素对坐标计算的影响,在原LANDMARC算法获取理论坐标后,将调用自修复机制第二阶段坐标修复过程,对目标位置进行适当修正,该坐标修复过程具体步骤如下:
(1)获取目标理论位置。LANDMARC算法选择出目标的K个最近邻参考标签,通过加权求和公式获得目标的理论位置(x,y);
(2)得到与目标最近参考标签的实际位置。取上一阶段关联度修复中的最小非零关联度值Emin,同时遍历全部参考标签,得到拥有最小关联度值的参考标签个数为n,而这n个参考标签的坐标实际位置是已知的,记为(x1,y1),(x2,y2),…,(xn,yn);


(5)修正目标坐标位置。用第一步获得的目标理论位置减去坐标修复值β,可修正坐标定位中产生的部分误差,修正后定位结果(x,y)=(x,y)-β(x,y)。
2.2 算法设计
改进的LANDMARC定位算法在经典LANDMARC算法过程中引入了自修复机制,分为两部分,即在关联度计算后进行关联度修复,以及在理论坐标位置计算后进行坐标位置修正。该机制生成关联度修复值α以及坐标修复值β,对引发定位过程紊乱的异常关联度值进行修复,同时修正RSSI值测量偏差引发的坐标误差,提高了定位精度,使LANDMARC算法具有自我修复能力。该改进算法的主要步骤如下:
第一阶段:获取信号强度矩阵。
该阶段是LANDMARC算法定位过程中最基础的阶段,所有参考标签与目标的RSSI值都是在该阶段获取。假设该定位区域有n个RFID阅读器,m个参考标签和u个待测的目标标签。在第一阶段,RFID阅读器读取定位区域内所有参考标签与目标的信号强度等级,得到参考标签信号强度矩阵A和目标标签信号强度矩阵S。
其中,Aij(i=1,2,…,m,j=1,2,…,n)表示第j个阅读器读取到的第i个参考标签的信号强度等级值;Sij(i=1,2,…,m,j=1,2,…,n)表示第j个阅读器读取到的第i个目标标签的信号强度等级值。
有了参考标签信号强度矩阵A和目标信号强度矩阵S作为基础,就能够在后面的阶段中对参考标签和目标标签的关联度进行估算。
第二阶段:计算关联度,同时实现自修复机制Ⅰ:关联度修复。
关联度值是参考标签和目标标签距离远近的数值表示,关联度值越小,说明两个标签之间的距离越相近。LANDMARC算法只知道参考标签的位置,而不知道目标标签的实际位置,但是通过对阅读器中读取到的信号强度等级值比较,能够判断出双方之间的距离远近。也就是说,当参考标签和目标标签之间的距离相近时,它们在同一个RFID阅读器中获取的值也是接近的。因此,LANDMARC算法在这个阶段找出参考标签与目标的关联,得到关联度矩阵E。
其中,Eij(i=1,2,…,m,j=1,2,…,u)表示第i个参考标签与第j个目标标签的关联度,可利用均方差公式来计算:
(3)
计算得到的关联度值,能够直观体现出目标与标签的距离远近程度,用于选择出在计算目标标签坐标定位时占比重最大的K个邻居标签。
由于RFID阅读器读取值信号强度等级值具有离散性,当参考标签与目标标签位置极近时,它们之间的关联度Eij可能为零,这会导致第四阶段使用的权重公式wi发生错误。因此,利用式(3)得到参考标签与目标标签的关联度矩阵后,执行自修复机制的第一部分关联度修复过程,对矩阵内所有参考标签和目标标签的关联度进行检测,如发现存在零值的异常关联度,则通过式(2)生成修复值α进行替换,以保证定位过程中不会出现值为零的关联度,使LANDMARC算法具有稳定性。
第三阶段:选择K个最邻近标签。
由于参考标签的位置是已知的,在第三阶段中需要确定K个参考标签作为计算目标位置信息时提供位置信息的最近邻居。这K个最近邻居的选择依据在第二阶段中所计算的参考标签与该目标的关联度值,选取关联度最小的K个参考标签作为目标的最近邻,并对它们进行重新编号,也就是“k近邻算法”。
该阶段是影响LANDMARC算法定位精度的重要阶段,最近邻居数K值的不同取值影响着算法平均误差。若K取值过大,会导致大量与目标相距较远的不良标签被引入,使定位产生较大误差;而K取值过小,则会因选取参与定位的参考标签过少而使目标的位置计算存在偶然性,因此合适的K值对基于LANDMARC的室内定位系统起到了重要的作用,后续实验将讨论对于该改进的LANDMARC算法的最佳K值。
第四阶段:计算目标位置,同时进行自修复机制Ⅱ:坐标修复。
第四阶段是LANDMARC算法用k个邻居参考标签位置对目标的最终定位阶段。该阶段使用权重质心法,通过加权求和来确定目标标签的理论位置(x,y),即使用如下公式:
(4)
这里参与目标定位的k个位置信息即为第三阶段中选出的与目标最近的K个参考标签位置坐标。其中ωi表示第i个邻居标签在式(4)中所占权重,理论上越接近目标的邻居标签在目标定位时所占权重应越大,因此通过第二阶段计算的关联度值来衡量权重的大小,其计算公式为:
(5)
式(5)为二阶权值定义法,关联度E越小,距离目标越近,被分配的权值越大,但当Eij=0时,该权重公式将发生错误,因此需要在第二阶段进行关联度修复,以防止发生定位紊乱。通过式(4)和式(5)能够计算出第j(j=1,2,…,u)个目标标签的理论位置。
受多径效应影响,该理论位置与目标实际位置有一定偏差。在获得目标的理论位置之后,进行自修复机制的坐标修复,遍历全部参考标签,找到与目标关联度最小的参考标签,继续对参考标签使用LANDMARC算法,利用k最近邻计算出参考标签理论位置,将参考标签理论坐标与已知的实际坐标相减,并求取平均值,即得出坐标修复值β(x,y)。最后将目标标签的理论位置减去坐标修复值β(x,y),获得目标标签修正后的实际坐标为:(x,y)=(x,y)-β(x,y)。
2.3 算法流程
图1为改进的LANDMARC算法流程图。
通过图1可知,该改进算法在原算法流程中新增了自修复机制,在关联度计算结束后进行关联度修复,同时对加权求和后得到的目标理论坐标位置进行修正,进一步改善了定位精度,提高了算法运行稳定性,使算法具有自我修复能力。
3 仿真实验
3.1 仿真环境
使用Matlab对改进的LANDMARC算法进行仿真实验,利用对数距离路径损耗模型,取路径损耗指数n为2.2,模拟了RFID阅读器读取的标签信号强度值。整个定位区域是一个10*10的正方形空间,在这个定位区域安置了5个目标标签和4个读取信号强度等级值的RFID阅读器,以及用于辅助定位的参考标签为11*11个,其中5个目标标签标号1~5的坐标位置分别为(2,4),(5,5),(6,6),(3,3),(4,2)。整个定位的布局如图2所示。

图1 算法流程

图2 环境布局图
3.2 结果与分析
3.2.1 改进算法最佳K值
经典LANDMARC算法的最佳K值为4,而改进LANDMARC算法对目标位置进行修正,导致改进算法的最佳K值可能发生变动。为了使改进算法能够发挥出其最优秀的定位性能,需要通过仿真实验找到改进的LANDMARC算法的最佳K值。
用图2的布局环境对不同K取值下的改进算法进行仿真,并定义误差公式为:
(6)
其中,(x0,y0)为目标的实际位置;(x,y)为目标的估测位置。
通过仿真,得到改进算法在不同K取值下的误差结果,如图3所示。

图3 误差折线图
通过图3能够清楚地观察到在不同K取值下误差的变化趋势。发现当K=6时,该改进算法拥有最小的平均误差和最大误差,其中平均误差低于0.1,虽然算法取K=5在目标4时获得了所有K取值中最小的误差,但其最大误差较大。纵观全体趋势,认为K=6是改进LANDMARC算法的最佳K值,与普通LANDMARC算法中最佳K值不同。在后续仿真中,将改进算法的K值取为6,以充分发挥该算法的最佳性能。
3.2.2 算法仿真结果
运用文献[10]的LANDMARC算法,用图2所示的布局环境,进行目标节点的定位仿真,其仿真结果如图4所示。
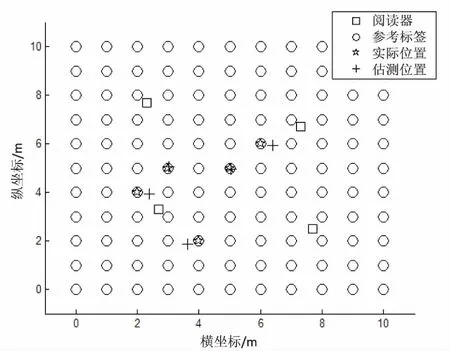
图4 LANDMARC算法定位结果图
而根据3.2.1小节的分析,选取改进LANDMARC算法的最佳邻居数K值为6,对改进的LANDMARC算法在相同的参数环境下进行仿真,定位结果如图5所示。
从图4、5可以看出,改进的LANDMARC算法有更好的定位精度,所有目标节点的定位误差都较小,不易发生较大的定位偏差,更具稳定性,因此算法在优化定位方面效果较为理想。

图5 改进算法定位结果图
3.2.3 误差分析
由图4、5的定位结果,按照式(6)作为误差公式,得出了在相同环境下文献[10]中LANDMARC算法与文中改进LANDMARC算法对五个目标定位的误差对比,如图6所示。
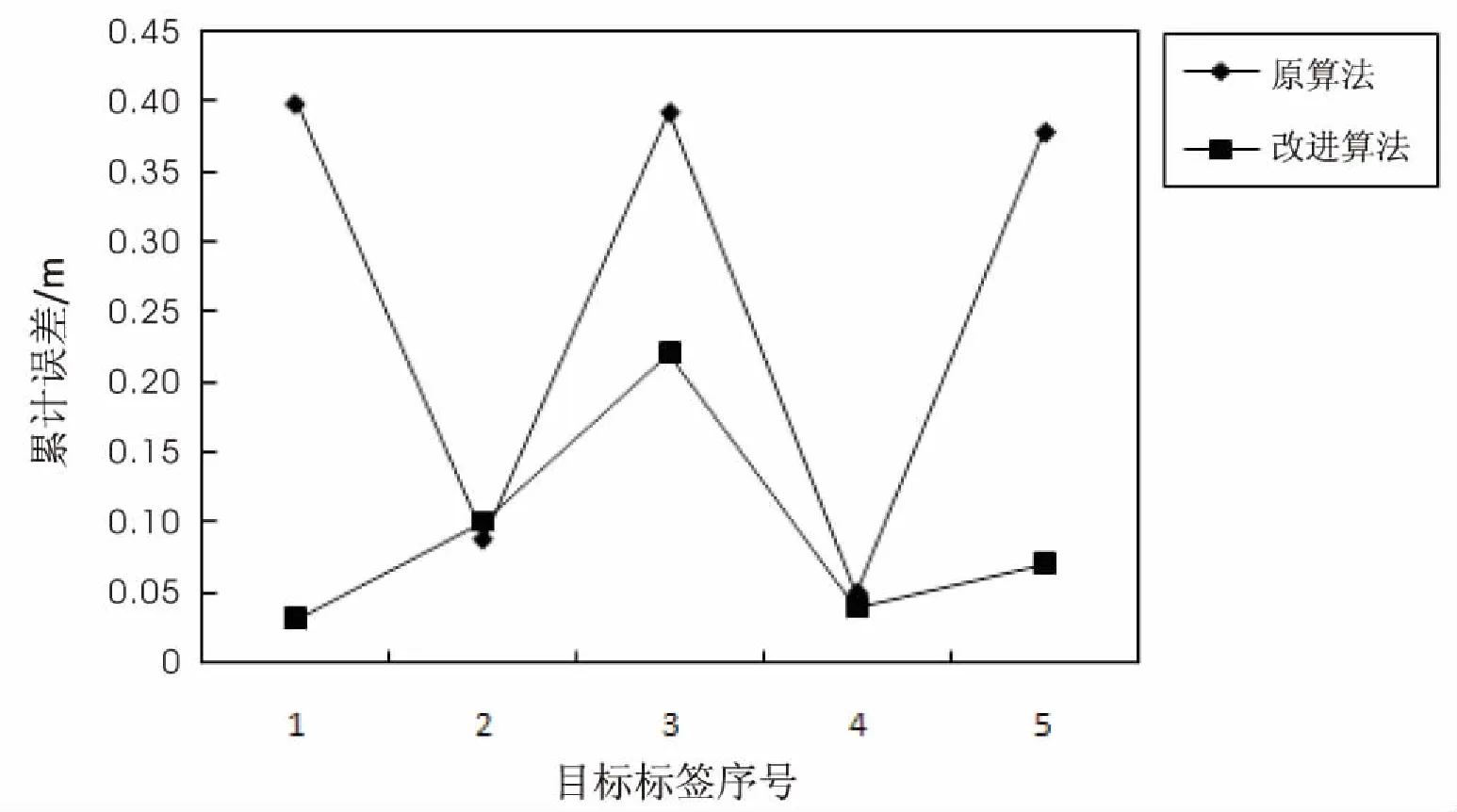
图6 误差对比图
从图中可以发现,改进算法始终处于下方,定位误差较小,均稳定在0.25以下,而为了能更直观地观察出算法定位精度及其稳定性,计算出原算法的平均误差、最大误差、标准差分别为0.264,0.399,0.157 5,而改进算法则为0.092,0.221,0.068 3。由以上数据可以看出,改进算法在平均误差和最大误差上都更具优势,原LANDMARC算法在目标1、目标3、目标5均出现了达到0.4的较大误差,而改进算法将五个目标的定位误差均控制在0.25以下,有效修正了大误差的产生。同时,原算法误差波动很大且标准差较大,而改进算法产生的误差趋势较为平稳,标准差较小,说明改进算法在相同环境下具有更高的定位精度和稳定性,算法具有自我修复能力。
4 结束语
针对LANDMARC算法定位过程中易引发的定位异常和坐标位置偏差,提出一种改进的LANDMARC室内定位算法。该算法引入自修复机制,对异常关联度和坐标位置进行修复,使算法具有自我修复能力。实验结果表明,该算法具有更高的定位精度,能有效避免发生较大的定位偏差,同时定位过程稳定性更高。当然,自修复机制的引入会导致算法复杂度的提升,带来定位过程中多余的能量消耗,今后的工作将着重于LANDMARC算法复杂度以及能耗方向的研究。
[1] 席 瑞,李玉军,侯孟书.室内定位方法综述[J].计算机科学,2016,43(4):1-6.
[2] 闫兴亚,陆 可,刘 伟.基于WiFi定位技术的增强现实室内向导研究与应用[J].计算机应用与软件,2016,33(5):108-111.
[3] 王中生,曹 琦.基于ZigBee技术的无线定位研究与实现[J].计算机技术与发展,2010,20(12):189-192.
[4] 刘 熙,刘开华,马永涛,等.多径环境下无源超高频RFID定位算法研究[J].计算机工程,2014,40(8):33-37.
[5] 肖 竹,王勇超,田 斌,等.超宽带定位研究与应用:回顾和展望[J].电子学报,2011,39(1):133-141.
[6] 王 睿,赵 方,彭金华,等.基于WI-FI和蓝牙融合的室内定位算法[J].计算机研究与发展,2011,48:28-33.
[7] NI L M,LIU Y H,LAU Y C,et al.LANDMARC:indoor location sensing using active RFID[C]//Proceedings of the first IEEE international conference on pervasive computing and communications.Washington DC,USA:IEEE Computer Society,2003:407.
[8] JIN G,LU X,PARK M S.An indoor localization mechanism using active RFID tag[C]//IEEE international conference on sensor networks,ubiquitous,and trustworthy computing.Washington DC,USA:IEEE Computer Society,2006:40-43.
[9] 吴王润.基于改进LANDMARC算法的RFID室内定位系统研究与实现[D].长沙:中南大学,2014.
[10] SANSANAYUTH T,SUKSOMPONG P,CHAREONLARPNOPPARUT C,et al.RFID 2D-localization improvement using modified LANDMARC with linear MMSE estimation[C]//13th international symposium on communications and information technologies.[s.l.]:[s.n.],2013:133-137.
[11] 练柱先,余 江,徐丽敏.一种改进的LMMSE信道估计算法[J].计算机科学,2014,41(4):53-56.
[12] YEH C H,SU S F.Enhance LANDMARC from the fundamentals[C]//International conference on advanced robotics and intelligent systems.[s.l.]:[s.n.],2013:23-27.
[13] 周亚罗,程锐涵,王莎莎.基于RSSI的LANDMARC室内定位算法的改进[J].河北联合大学学报:自然科学版,2016,38(2):87-91.
[14] 代琪怡.距离无关的室内路径损耗模型的建立[D].重庆:重庆理工大学,2014.
[15] 鱼璐璐,杨智应.改进的LANDMARC定位算法[J].硅谷,2012(3):185-187.
[16] 张晓丹,黄海燕.基于免疫克隆算法的LVQ聚类算法权值优化[J].计算机科学,2013,40:27-28.
[17] LU S,XU C,ZHONG R Y.An active RFID tag-enabled locating approach with multipath effect elimination in AGV[J].IEEE Transactions on Automation Science and Engineering,2016,13(3):1333-1342.

