基于复杂网络的供应链网络演化模型研究∗

丁 飞 陈 红 杨冀豫

（1.中北大学创新研究中心 太原 030051）（2.中北大学电子测试技术国家重点实验室 太原 030051）

1 引言

随着全球一体化的深入，供应链网络的规模不断扩大，结构不断扩展，迫切需要供应链管理者运用新的理论和方法，研究供应链网络的结构特性［1］。近年来，随着复杂网络领域中BA无标度网络的发现，使得复杂网络成为多个学科共同关注的前沿热点，被广泛应用在管理学、社会学领域［2］。

自从 1999 年Barabási和 Albert［3］提出BA网络演化模型之后，目前大部分学者对供应链网络的研究，都先后采用BA网络模型。刘燕楚等［4］提出了连接路径的概念，并以此作为择优连接的测度指标，但是学者们只研究了节点的进入，缺乏对节点退出行为的研究。曹文彬等［5］认为供应链网络中存在效益较低而合作失败的现象，进而研究了边退化行为。李广等［6］也研究了节点企业加入和退出的行为，结果表明，供应链网络服从幂率分布。但学者们对于网络中节点的退出，大都认为节点的退出是一蹴而就的行为，不符合实际网络中，节点之间的合作连接逐步断开的情况。同时，学者们在研究供应链网络时，缺乏对节点补偿行为的研究。

常兰［7］认为供应链网络的演化会历经产生、发展、成熟和衰落的阶段，即供应链网络有自己的生命周期。但未有学者从生命周期角度研究供应链网络的演化特征。

所以，本文在BA模型的基础上，研究节点进入、退出和补偿行为下的供应链网络，并首次将供应链生命周期引入到供应链网络演化模型中，分析供应链网络演化与生命周期的关系。

2 供应链网络演化模型的建立

2.1 演化模型算法

在供应链网络中，本文将网络中的厂商看作“节点”，厂商之间发生的联系作为“边”［8］。

厂商在进入供应链网络中时，会受到进入壁垒和退出壁垒的影响［9］，因而厂商的进入与退出行为不是肯定会出现的，而是以某种概率出现。本文假设厂商进入的概率为p，退出的概率为q（0＜p＜1，0＜q＜1）。

网络中最初有m0个节点，在演化的过程里，历经下列三种情形：

1）以概率p增加一个新节点，该新节点拥有m(m≤m)条新边，每条新边以概率择优连

0接到网络中已存在的节点i上，其中ki表示节点i的度，表示网络节点度的总和。

2）从供应链网络中随机选择n条边，每条边以概率q断开。

3）本文考虑的补偿机制具体细分为两种情形：一方面，如果供应链网络中的某节点i失去一个连接，那么该节点将会补偿得到h条连接（h＜hcrit(q)，这里hcrit(q)是与断开概率q有关的上限）；另一方面，在每个时间步长里，节点i总是在不断地与网络内的其他厂商建立合作连接，本文假设以概率r建立l条连接，这些连接与i的合作也遵循择优连接［10］。

2.2 演化模型的节点度分析

当供应链网络演化到t时刻时，向网络中加入的节点厂商数的期望是pt；向网络中添加边的期望是pmt+qht+rlt；断开边的期望是qnt。所以，在t时刻供应链网络中共有m0+pt个节点，pmt+qht+rlt-qnt条边，从而得到供应链网络中节点度的总和是：

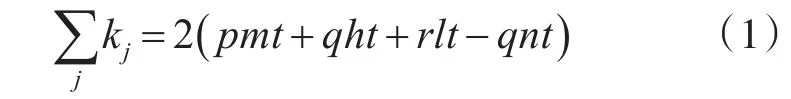
对于在ti时刻新加入到供应链网络中的节点i，ki(ti)=m。

根据连续域理论［11］，可得供应链网络演化的三种情况下节点i的度的变化率为

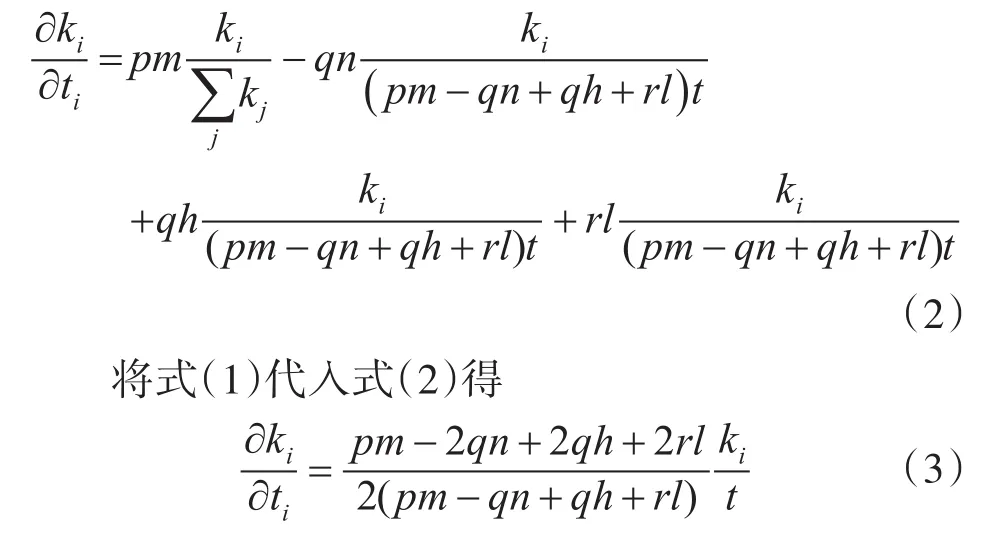
代入节点i的初始条件，ki(ti)=m并求解式（3）的微分方程，得到

由式（4），节点 i的度 ki(t)小于 k的概率p[ki(t)＜k]可表示为

所以，供应链网络节点度分布的概率密度函数p(k )～ k-γ，且指数 γ为

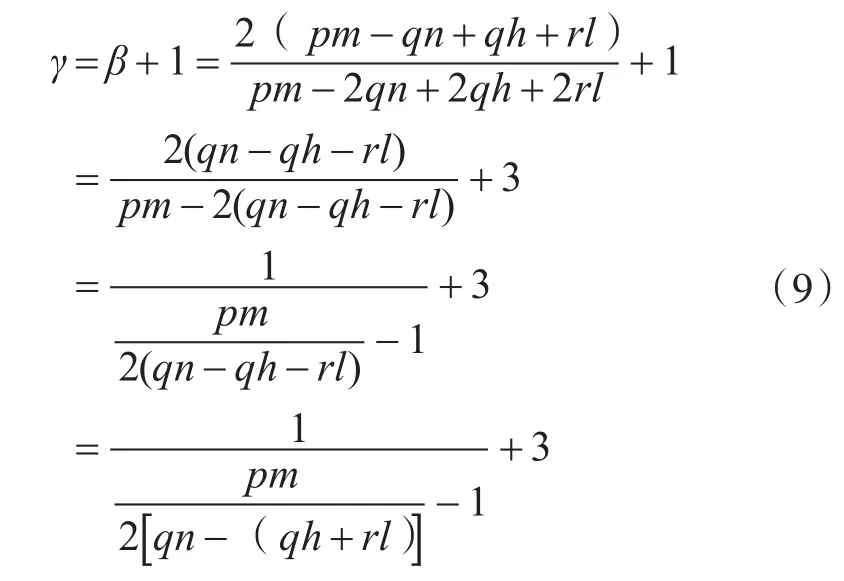
从式（8）可以看出，供应链网络的演化具有无标度特征。当供应链网络中断开连接的速度等于补偿连接的速度时，即qn=qh+rl，模型退化为BA模型，γ=3。从式（9）可知，厂商进入网络、退出网络和补偿的速度共同决定了幂律分布的指数γ。

3 供应链网络演化模型分析

3.1 供应链网络仿真分析

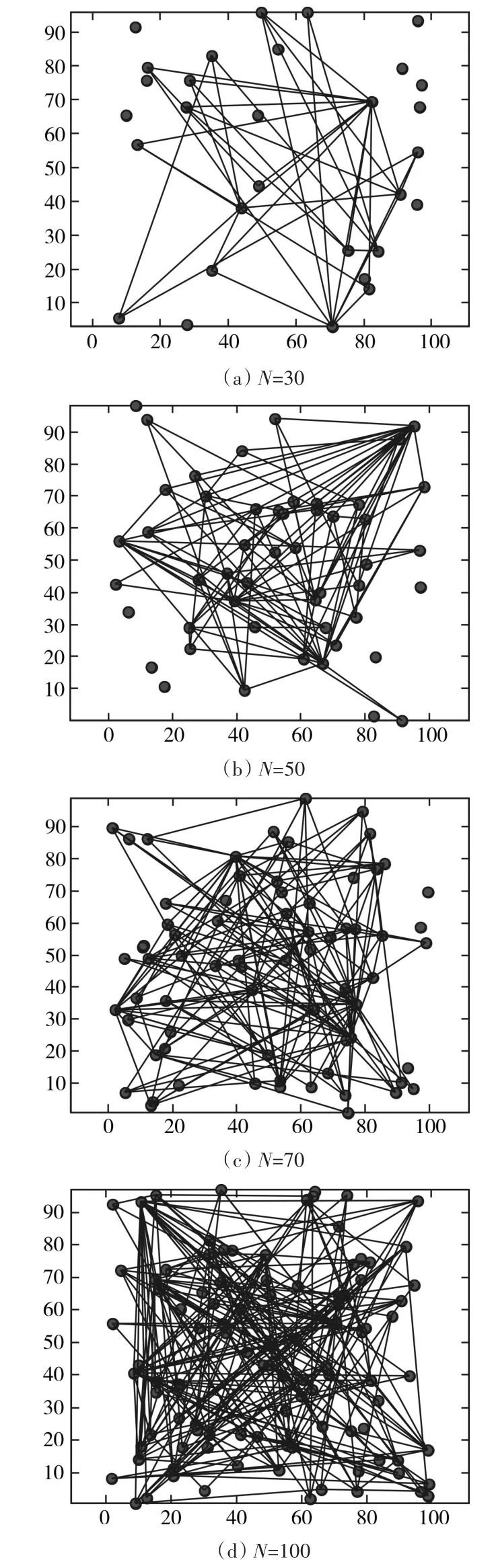
图1 供应链网络动态演化拓扑图

在供应链网络中，厂商在选择合作伙伴时并不是随机的，而是基于自身的需求和对方满足需求的基础［12］。依据市场竞争的原则，厂商将会优先选择具有竞争优势的厂商作为合作伙伴［13］，体现了BA网络择优选择的特点。这种择优选择的行为是供应链网络形成的基本原则，因而这种机制下的供应链网络，其形成和发展服从幂律分布［14］，具有无标度的特征。

本文采用Matlab工具，对供应链网络的演化过程进行仿真，验证供应链网络演化模型的无标度特性。实验中，m0=15，p=0.7，m=3，q=0.6，n=7，h=3，r=0.6，l=1。图 1中（a）（b）（c）（d）分别是节点数量达到30，50，70，100时，供应链网络演化仿真的拓扑结构状。

通过对供应链网络中各个节点的度进行统计，进而得到节点度的大小分布图，如图2、图3、图4所示，图2为 m0=15，p=0.7，m=3，q=0.6，n=7，h=3，r=0.6，l=1，N=100的节点度的大小分布图，图3为 m0=15，p=0.7，m=3，q=0.08，n=7，h=3，r=0.6，l=1，N=100的分布图，图4为 m0=15，p=0.7，m=3，q=0.6，n=7，h=3，r=0.07，l=1，N=100的分布图。

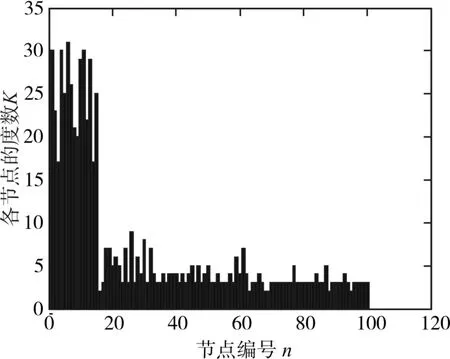
图2 节点度的大小分布图（p=0.7q=0.6r=0.6）

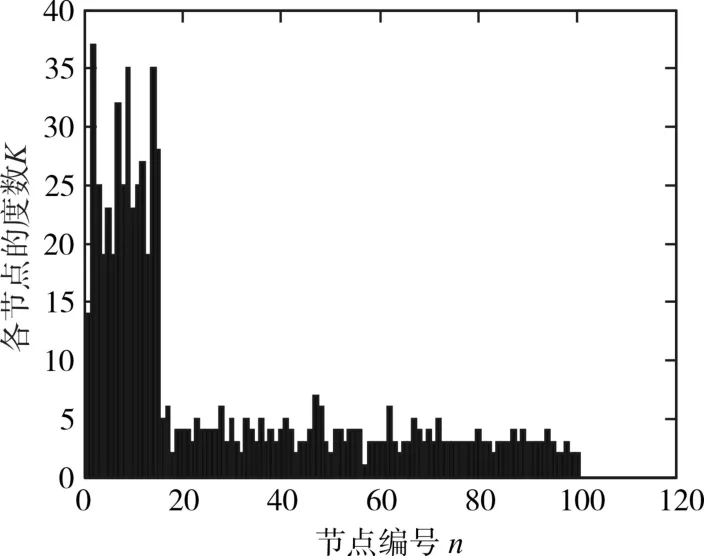
图3 节点度的大小分布图（p=0.7q=0.08r=0.6）

当q取值极小时，网络中断开的连接数量较少，也极少有节点退出，此时供应链网络的状态稳定，发展势头较好。但在现实中企业想达到这种状态，需要极大的成本［15］。从图2和图3看出，随着q的减小，网络中大部分节点的度值增大，但都存在节点度较大的核心节点，表现出无标度的特性。

当r取值极小时，网络中补偿合作的连接数增长幅度较慢，网络发展缓慢。从图2和图4看出，随着r的减少，网络中节点的度值呈现下降的趋势，其中，最大的节点度值也只能到达30的界限，但也都表现出无标度的特性，服从幂律分布的特点。

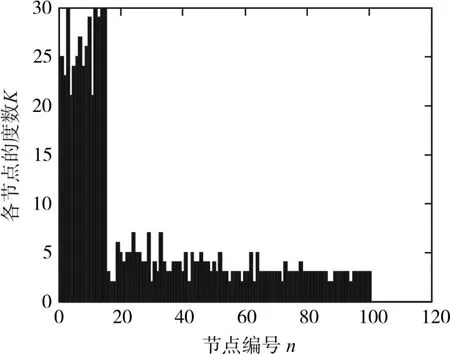
图4 节点度的大小分布图（p=0.7q=0.6r=0.07）

3.2 供应链网络演化与生命周期的关系

3.2.1 供应链网络规模变化

由演化模型的条件可知，pm为厂商进入供应链网络的速度，qn为厂商退出过程中连接断开的速度，qh+r为l厂商因失去连接而获得补偿连接的速度，从式（9）可知，厂商进入网络、退出网络和补偿的速度共同决定了幂律分布的指数γ。同时，这三者的速度也决定了供应链网络规模的变化，所以可得到如下讨论结论：

1）当qn≤qh+rl时，供应链网络中断开连接的速度小于补偿连接的速度，总的来看，网络中的连接处于增加的趋势，因而供应链网络是一个增长的网络，随着时间的演化，供应链网络的规模（节点数和连接数）会越来越大。

3.2.2 供应链网络演化与生命周期的关系

厂商进入网络、退出网络和补偿的速度不仅影响了网络整体的规模，也影响供应链网络所处的生命周期的阶段。依据供应链网络所处生命周期各个阶段的特点，研究供应链网络演化过程中，进入速度pm、退出速度qn和补偿速度qh+rl对其生命周期产生的影响。

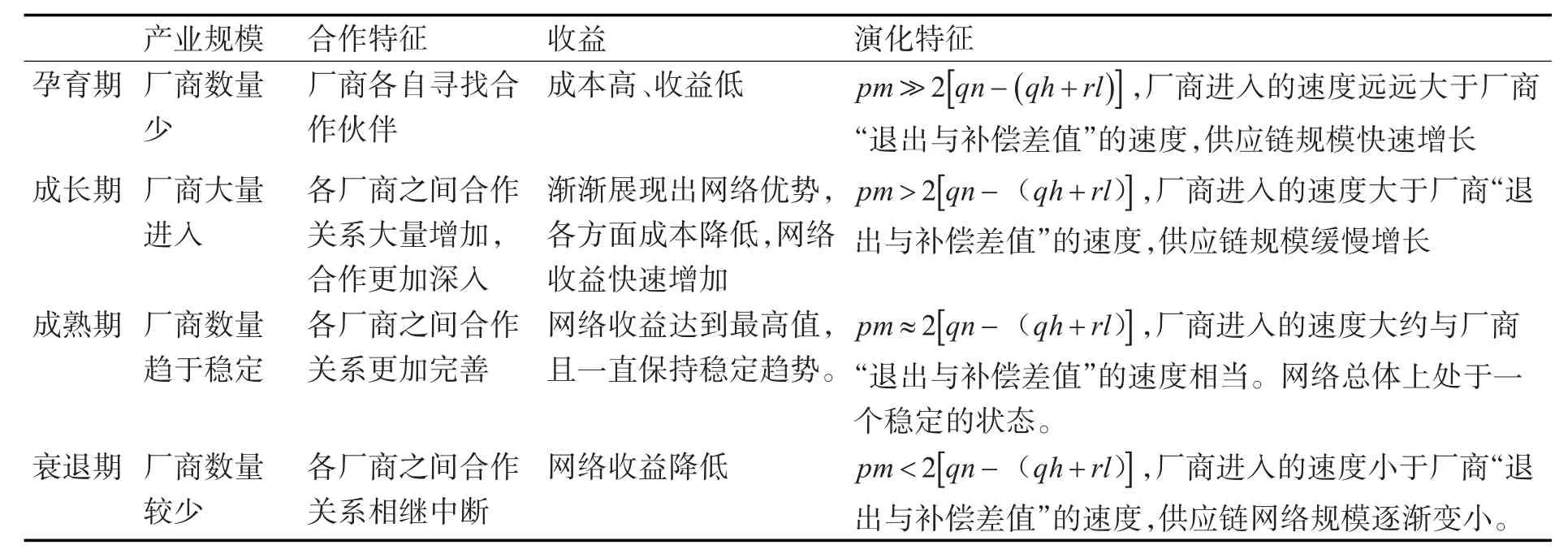
表1 供应链网络演化与生命周期的关系

4 结语

本文将供应链网络视为由众多厂商成员，根据彼此间的经济合作与竞争关系，在空间网络上形成的复杂网络。1）考虑厂商的逐步退出过程，主要从厂商节点进入、退出和补偿机制三方面对对供应链网络进行模型的构建。2）通过对供应链网络演化模型的度分布及幂指数γ的推导，得出供应链网络的演化状态主要由网络演化规则中的p、m、q、n、h、r、l等变化参数所控制。3）对网络演化过程进行仿真分析，进一步表明供应链网络是无标度网络。4）通过分析网络的演化与供应链生命周期所处的阶段的关系，发现厂商进入速度pm，退出速度为qn，获得补偿速度qh+rl，决定了供应链网络的生命周期所处的阶段，对供应链网络的结构也造成很大的影响。

但是本文在构造供应链网络模型时，假设所有厂商节点均具有同质性，没有考虑厂商的节点异质性问题，这是本文的不足之处，也是未来的研究方向。

［1］T.Y.Choi，K.J.Dooley.Supply networks and complex adap⁃tive systems：control versus emergence［J］.Journal of Op⁃erations Management，2001，19（3）：351-366．

［2］Hang W，Xu M，Chen X，et al.Vessel traffic flow predic⁃tion model based on complex network［C］//International Conference on Transportation Information and Safety.IEEE，2015：473-476.

［3］Barabási A L，Albert R，Jeong H.Mean-field theory for scale-free random networks［J］.Physica A Statistical Me⁃chanics&Its Applications，1999，272（1-2）：173-187.

［4］傅培华，李进，刘燕楚.基于度与路径优先连接的集聚型供应链网络演化模型［J］.运筹与管理，2013（1）：120-125.

FU Peihua，LI Jin，LIU Yanchu.clustersupply chain net⁃work evolving model based on degree and path preferential attachment［J］.Operations Research and Management Sci⁃ence，2013（1）：120-125.

［5］曹文彬，熊曦.边效益因素下复杂供应链网络局域演化机制［J］.计算机应用研究，2016，33（1）：75-77，81.

CAO Wenbin，XIONG Xi.Local-world evolution model of complex supply chainnetwork under edge benefit［J］.Ap⁃plication Research of Computers，2016，33（1）：75-77，81.

［6］李广，赵道致.供应链网络的无标度特性研究［J］.工业工程，2012，15（1）：28-32.

LI Guang，ZHAO Daozhi.A Study on the Scale-Free Char⁃acteristics of Supply Chain Network［J］.Industrial Engi⁃neering Journal，2012，15（1）：28-32.

［7］常兰.制造企业供应链生命周期质量管理技术研究［D］.重庆：重庆大学，2012.

CHANG Lan.Manufacturing enterprise supply chain life cycle quality managementtechnology research［D］.Chongqing：Chongqing University，2012.

［8］Amit Surana，Soundar Kumara，Mark Greaves，et al.Sup⁃ply-chain networks：a complex adaptive systems perspec⁃tive［J］.International Journal of Production Research，2005，43（20）：4235-4265.

［9］Zhang N，Mao G.A Multilevel Simplification Algorithm forComputingtheAverageShortest-Path Length of Scale-Free Complex Network［J］.Journal of Applied Mathematics，2014（4）：1-6.

［10］刘绘珍.基于组织进入、退出和合作的技术创新网络演化模型［J］.数学的实践与认识，2016（6）：23-29.

LIU Huizhen.Base on organized into enter and exit and cooperative technology innovation networks model［J］.Mathematics in practice and theory，2016（6）：23-29.

［11］Che Z H，Chiang T A，Kuo Y C，et al.Hybrid algorithms for fuzzy reverse supply chain network design［J］.Thesci⁃entificworldjournal，2014（1）：497109.

［12］彭永涛，张锦，王坤.具有随机供需特征的物流超网络优化模型研究［J］.交通运输系统工程与信息，2014，14（2）：184-191.

PENG Yongtao，ZHANG Jin，WANG Kun.Logistics Su⁃pernetwork Optimization Model with Stochastic Supply and Demand Characteristics［J］.Journal of Transporta⁃tion Systems Engineering and Information Technology，2014，14（2）：184-191.

［13］Understanding supplier structural embeddedness：A so⁃cial network perspective［J］.Journal of Operations Man⁃agement，2014，32（5）：219-231.

［14］张广胜，刘伟.基于复杂网络理论的物流服务供应链网络脆弱性机理研究［J］.商业经济与管理，2016（12）：19-27.

ZHANG Guangsheng，LIU Wei.Mechanism of Network Vulnerability of Logistics SerVice Supply Chain Based on Complex Network Theory［J］.Journal of Business Eco⁃nomics，2016（12）：19-27.

［15］Nagurney A.Optimal supply chain network design and re⁃design at minimal total cost and with demand satisfaction［J］.International Journal of Production Economics，2010，128（1）：200-208.

［16］Zhang X，Adamatzky A，Yang X S，et al.A Physarum-In⁃spired Approach to Optimal Supply Chain Network De⁃sign at Minimum Total Cost with Demand Satisfaction［J］.Eprint Arxiv，2014.