基于局部空间信息的阈值分割算法∗

张弘 高威

（西安邮电大学自动化学院 西安 710121）

1 引言

图像分割是一种重要的图像分析技术。在对图像的研究和应用中，人们往往仅对图像中的某些部分感兴趣，这些部分常常被称为目标或前景（其他部分称为背景）。图像分割就是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣的目标的技术和过程，它是由图像处理到图像分析的关键步骤。现有的图像分割方法主要分为以下几类：基于阈值的分割方法［16］、基于区域的分割方法、基于边缘的分割方法［5］以及基于特定理论的分割方法等。在众多的图像分割方法中，阈值分割是普遍使用的最为有效的图像分割方法。在过去的几十年中，研究人员提出了许多阈值算法来确定最佳阈值［1］，不同的阈值方法可以在文献中找到。一般来说，阈值分割一般可以分为单级和多级阈值分割方法［2］，在单级阈值分割方法中，图像是基于单个阈值划分为两个不同的区域。相比之下，多级阈值是基于多个（多于一个）阈值将图像分割成几个不同的区域［7～12］。一个简单的方法是使用直方图找到最佳阈值。Otsu方法［14］是广泛使用的直方图阈值法，选择一个通过最小化类内方差来确定最优阈值［7］。文献［15］定义了一个标准假设不同区域中的像素是正态分布的，并且通过获得最佳阈值优化贝叶斯危险因素。另一种方法是最大化不同区域中的像素的熵以获得最优阈值［13～14］。文献［12］提出了一种基于集群的阈值技术，其中将数据分组使用相似性度量来进行聚类。

这些阈值方法具有一个主要缺点，大体上说，这些方法没有考虑到局部空间信息，对于某些图像分割效果不好，为了改进这个缺点，本文提出一种局部活动特征计算每个灰度值处的局部图像属性，通过对不同图像的类型进行评估，然后比较所提出的方法的结果与现有方法结果的比较，证实了本文提出的方法的有效性。

2 阈值分割方法及应用

2.1 迭代阈值分割算法

迭代阈值分割算法是一种基于逼近的思想，它首先选择一个近似阈值T，将图像分割成两部分，计算区域C0和C1的均值u0和u1，选择新的分割阈值，重复上述的步骤，直到u和u不01再变化为止。步骤如下：

步骤1：求出图像的最大灰度值和最小灰度值，分别记为Zmax和Zmin，令初始阈值。

步骤2：根据阈值T将图像分割为前景和背景，分别求出两者的平均灰度值Z0和Z1。

步骤4：如果两个平均灰度值Z0和Z1不再变化（或T不再变化），则T为阈值；否则转到步骤2），迭代计算。

迭代法所得的阈值分割的图像的效果良好。基于迭代的阈值能区分出图像的前景和背景的主要区域所在，但在图像的细微处下角深色区还没有很好的区分度。对某些特定图像，微小数据的变化却引起分割效果好的巨大变化。如图1（b）为迭代法分割rice图像的效果。

图1 米粒原图及其分割结果

2.2 传统的Otsu阈值分割方法

大津法（OTSU）是由大津于1979年提出的动态阈值分割算法，它的基本思想是利用图像的灰度直方图，以目标和背景的方差最大来动态地确定图像的分割阈值。基本原理如下，假设原始图像的灰度级为L，总像素个数为N，ni为灰度为i的像素个数，则每个灰度的概率：pi=niN，根据阈值T将图像分为两类：C0和C1，其中C0类的灰度范围为0～T，C1类的灰度范围为T+1～L-1，C0和C1比例分别为 和 ，C0和C1的灰度均值为

图2是对硬币的图像进行大津法的阈值分割，图（b）为大津法分割图像，如下图所示。

图2 硬币原图及其分割结果

2.3 基于邻域均值的分割算法

众多实验得出，传统的Otsu法对于直方图呈现双峰分布的图像的分割效果较理想。然而，在实际图像中，由于噪声干扰等因素的影响，使得图像的灰度直方图分布不一定出现明显的峰和谷，此时仅利用灰度直方图得到的阈值并不能使图像分割得到满意的结果，往往还会产生严重的分割错误。这是因为像素灰度值仅仅反映了像素灰度级的幅值大小，并没有反映出像素与其邻域的空间相关信息。提出了一种结合像素邻域空间信息的改进Otsu阈值分割算法。

基本思想是：考虑到图像是由明、暗两类构成的，因此可以首先做一次粗分割，把最亮和最暗的部分提取出来，即把最有可能是目标和背景的像素点分割出来。而剩下的部分则可能既包含目标又包含背景，此时对这些像素点结合其邻域信息进行相应的处理。最后，对处理过的图像应用Otsu法二值化。

具体算法如下：

1）获取原图像 f(i，j)的直方图；

2）按灰度级从小到大遍历直方图，找到第一个峰和最后一个峰，相应的灰度值分别记为T0和T1。记Gmin、Gmax分别为图像的最小、最大灰度；

3）设 f(i，j)为原图像中像素点的灰度值，即f(i-1，j-1)、f(i，j-1)、f(i+1，j-1)、f(i-1，j)、f(i+1，j)、f(i-1，j+1)、f(i，j+1)、f(i+1，j+1)是其8个邻域像素的灰度值，若 f(i，j)＞T0且f(i，j)＜T1，则用

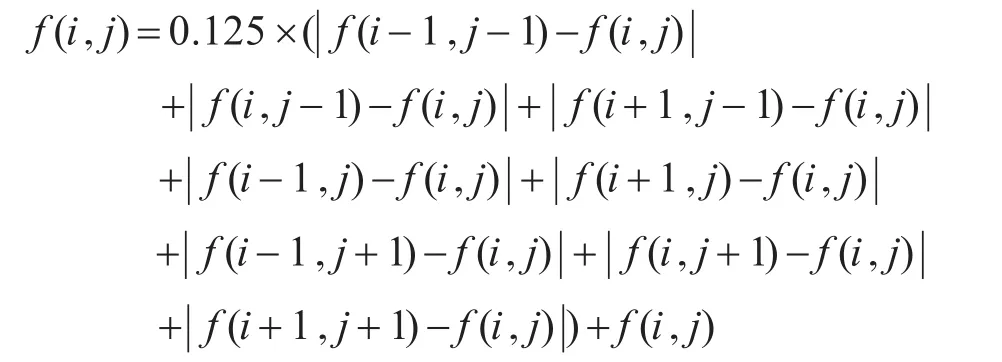
更新灰度值，否则该像素灰度值不变。

4）对经过上述处理过的图像采用Otsu法进行二值化处理，并选取最佳阈值。与传统的阈值分割方法进行比较，效果更佳，图3（b）为Otsu法分割图像，图3（c）为邻域均值法分割图像。

图3 夫妻原图及其分割结果

3 本文算法

大津法是较为经典的阈值分割算法，选取出来的阈值也较为理想，对各种情况的表现都较为良好。但是在很多情况下，大津法计算出来的都不是最佳阈值，由于图片本身，噪声等各种情况的干扰，仅利用直方图得到的阈值并不能使图像分割得到满意的效果，往往还会产生严重的错误。本文提出了一种结合局部空间信息的改进的阈值分割算法。

阈值分割法分为全局阈值法和局部阈值分割法。局部阈值分割法是将原始图像划分成较小的图像，并对每个子图像选取相应的阈值。在阈值分割后，相邻子图像之间的边界处可能产生灰度级的不连续性，因此需用平滑技术进行排除。局部阈值法常用的方法有灰度差直方图法、微分直方图法。

全局阈值分割方法［12］在图像处理中应用比较多，它在整幅图像内采用固定的阈值分割图像。经典的阈值选取以灰度直方图为处理对象。根据阈值选择方法的不同，可以分为模态方法、迭代式阈值选择等方法。这些方法都是以图像的直方图为研究对象来确定分割的阈值的。另外还有类间方差阈值分割法、二维最大熵分割法［1～3］、模糊阈值分割法［3］、共生矩阵分割法、区域生长法等等。

首先，图像中的邻域系统，常用的有3*3邻域系统，以中心点为中心，主要采用的是邻域平均法，以像素点 f(i，j)和其邻域中全部点的像素灰度均值替换像素点 f(i，j)的对应的灰度值，公式为

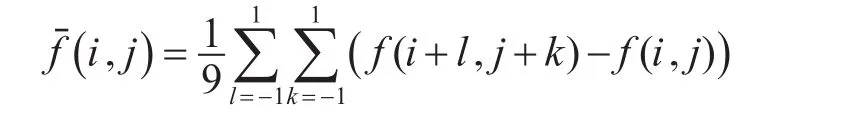
邻域均值方法是一种线性滤波方法，它主要是为了去除图像扫描的颗粒的噪声，主要采用的是邻域平均方法。邻域均值算法对于去除包含密度噪声图像噪声是一种比较有效的去除噪声方法，它利用灰度均值替换，达到去噪的目的。

第二步，再对图像进行邻域方差的计算，基于图像邻域3*3系统，计算出方差因子，公式为：

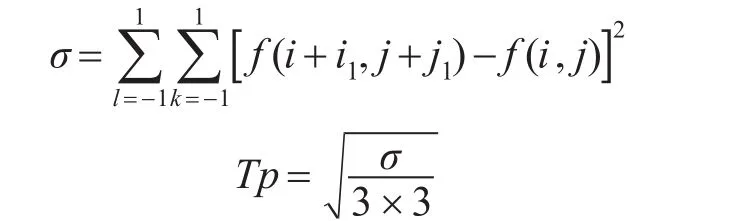
得出的Tp即为方差因子。第三步，进行图像融合，在图像的融合过程中，融合规则的选取是关键的一步，直接影响融合图像的质量。下面将方差因子与原图像进行融合，融合的公式为

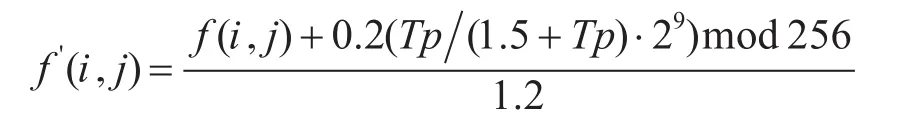
最后，对图像进行阈值分割。步骤为

步骤1：对于图像中的灰度级，找出它们的概率：

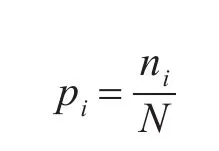
步骤2：令阈值为T，将图像分为两类：

步骤4：使用下面公式找到类间方差：

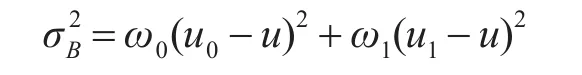
步骤5：通过类间方差最大化获得最优阈值：

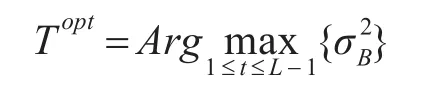
4 实验结果与分析

为了验证本文算法的有效性和可行性，实验选取了5幅普通图像，分别为cameraman、lena、老头、bird、sculpture图像，并与Otsu法进行了比较。实验系统为windows7系统，系统配置为3.2GB内存，3.19GHz，Matlab（R2014a），阈值的选取是本文的关键，对分割的结果有着重要的影响，以下实验发现本文提出的局部空间信息方法可以达到Otsu分割算法且优于Otsu分割算法。

比较下面几幅图，cameraman图像相较于迭代法和Otsu阈值分割法，本文算法将地上的附着物大致地显示出来，在细节方面处理的更好；lena图像的轮廓更加清晰；老头的图像的脸更加清楚，脸型更加分明；总体来说，从几幅图观察到本文分割方法分割效果更好，分割图像更接近原图。

图4 坛子原图及其分割结果

图5 lena原图及其分割结果

图6 老头图及其分割结果

图7 蝴蝶原图及其分割结果

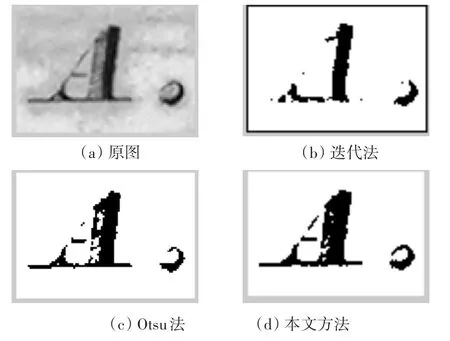
图8 字母原图及其分割结果

图9 怀表图及其分割结果

表1 三种方法阈值比较

5 结语

基于局部活动空间信息方法提出了一种新的阈值技术，针对文献［7］提出的采用局部阈值分割进行研究，结合全局阈值中的局部阈值法，提出了最近邻值阈值算法，对图像分割，阈值选取有更好的效果，但对于波峰和波谷接近的图像，此算法的效果并不明显，本文提出的分割算法在阈值选取上更加准确，且从肉眼可以观察到，该算法分割效果更好。

［1］BH ANDARIA K，KUMAR A，G.K.SINGH GK.Tsallis en⁃tropy based multilevel thresholding for colored satellite im⁃age segmentation using evolutionaryalgorithms［J］.Expert⁃Syst.Appl.2015，42（22）：8707-8730.

［2］PENG H，WANG J，JIMENEZ M J P.Optimal multi-level thresholding with membrane computing［J］.Digit.Signal Process.

［3］YIN S，ZHAO X，WANG W，GONG M.Efficient multilev⁃el image segmentation through fuzzy entropy maximization and graph cut optimization［J］.PatternRecognit.

［4］PANDA R，AGRAWAL S，BHUYAN S.Edge magnitude based multilevel thresholding using Cuckoo search tech⁃nique［J］.Expert Syst.Appl.40（18）（2013）7617-7628.

［5］SEZGIN M，SANKUR B.Selection of thresholding meth⁃ods for nondestructive testing applications［J］.Proceed⁃ings International Conference on Image Processing，2002（3）：764-767.

［6］HUANG L K，WANG M J.Image thresholding by minimiz⁃ing the measures offuzziness［J］.Pattern Recognit，1995，28（1）41-51.

［7］OTSU N.A threshold selection method from gray level his⁃tograms［J］.IEEE Trans.Syst.Man Cybern，1979，9（1）：62-66.

［8］LIM J S.Two-Dimensional Signal Image Processing［J］.Englewood Clis，NJ Prentice-Hall，1990，34（1）：6-8.

［9］CHANG C I，DU Y，WANG J，GUO S M，THOUIN P D，Survey and comparative analysis of entropy and relative en⁃tropy thresholding techniques［J］.IEE Proc.Vis.Image Signal Process，2006，153（6）：837-850.

［10］VOLOSHYNOVSKIY S，HERRIGEL N，BAUMGAERT⁃NER A，PUN T.A stochastic approach to content adap⁃tive digital image watermarking，Proceedings of Interna⁃tional Workshop on Information Hiding［J］.Lecture Notes in Computer Science，1999，1768（2）：211-236.

［11］KWON S H.Threshold selection based on cluster analysis［J］.Pattern Recognit.Lett.2004，25（9）：1045-1050.

［12］PUN T.A new method gray-level picture thresholding us⁃ing the entropy of the histogram［J］.SignalProcess，1980：223-237.

［13］KAPUR J N，SAHOO P K，WONG A K C.A new meth⁃od for gray-level picture thresh-olding using the entropy of the histogram［J］.Comput.Vis.Graph.Image Process，1985，29（3）：273-285.

［14］KITTLER J，ILLINGWORTH J，Minimum error thresh⁃olding［J］.Pattern Recognit，1986，19（1）：41-47.

［15］CHO S，HARALICK R，YI S.Improvement of Kittler and Illingworth，minimum error thresholding［J］.Pattern Recognit，1989，22（5）：609-617.

［16］吴成茂，田小平，谭铁牛.二维Otsu阈值法的快速迭代算法［J］.模式识别与人工智能，2008，12（6）：746-757.

WU C M，TIAN X P，TAN T N.A Fast Iteration Algo⁃rithm for 2-D Otsu Threshold［J］.Pattern Recognition and Artificial Intelligence，2008，12（6）：746-757.

［17］赵凤，惠房晨，韩文超.基于过分割的多目标阈值图像分割算法［J］.西安邮电大学报，2015，20（3）：60-64.

ZHAO F，HUI F C，HAN W C.SegmentationAlgorithm Based on Overset Multi-target Threshold［J］.Journal of Xi'an University of Posts and Telecommunications，2015，20（3）：60-64.