基于多状态贝叶斯网络的导弹质量状态评估

徐廷学， 李志强， 顾钧元， 丛林虎， 安进， 赵建忠

(海军航空大学 兵器科学与技术系， 山东 烟台 264001)

0 引言

采用自动检测设备对导弹进行质量状态评估时,结果只有“合格”与“不合格”两种，无法确切地获得导弹各项性能指标的优劣程度与变化规律。这种“是非制”评估方式过于粗放，造成了信息资源浪费，不满足“经济可承受性”要求。韩小孩等[1]、王少华等[2]利用关联维数分析对装备质量状态进行了等级划分，但是神经网络训练需要大量数据。王京等[3]应用贝叶斯理论对专家数据、摸底试验数据等5种常见先验信息进行折合以解决样本数据量小的问题，但是评估指标的精度有待进一步提高。王亮等[4]、丛林虎等[5]应用DS证据理论融合导弹性能特征参数，确定了导弹所处的质量状态等级。但是DS证据理论证据间容易出现冲突问题，文献[4-5]均假设各证据源具有相同的重要性。

鉴于文献[4-5]的三角隶属度函数过于粗放，本文在文献[6]的基础上确定了改进岭形隶属度函数。在具有确定性逻辑关系的贝叶斯网络(BN)模型中，结构参数由节点之间的与、或、非等逻辑关系确定[7-8]。在涉及非确定逻辑关系时，文献[9-11]提出了基于DS证据理论- 层次分析法(DS/AHP)的二元状态条件概率值(CPT)确定方法，而后由姚爽等[12]将其拓展应用到多属性群决策中。本文则在此基础上提出了多状态条件概率赋值方法，综合多位领域专家信息以降低不确定度。

1 导弹质量状态等级划分

根据检测设备的工作原理，如果导弹检测的所有性能参数都在规定的阈值范围内，则导弹的质量状态正常，否则就发生了故障。“合格”、“不合格”的“是非制”检测方式存在一定的弊端：对于质量状态良好的导弹进行经常性检测、维护，使得维修过剩而造成维修资源浪费；对于接近故障状态的导弹采用原有的检测与维护方式，使得维修不足而造成战备完好率下降。在充分考虑测试参数的基础上，将导弹状态划分为良好、较好、堪用、拟故障、故障5个等级，如表1所示。

由于受到环境应力的影响，如温度湿度异常、震动、盐雾等，导弹内部的某些电子元器件或者机械零部件性能指标下降，在电气属性测试时，表现为某些参数在阈值范围内不断变化。长时间的恶劣环境将使导弹性能逐渐退化，呈现出测试参数离标准值越来越远，离上下边界越来越近的趋势。因此，在导弹贮存中，一定注意做好“三防”工作，使温度、湿度处于“三七线”范围内。为确保导弹装备的战备完好性，对处于“堪用”和“拟故障”状态的导弹，可以视情缩短电气属性检测周期或者增加单元测试频次，及时安排维修保障工作。对处于故障状态的导弹，参照电气属性测试结果进行故障诊断与隔离，根据所在单位的维修级别进行下一步维修工作的安排。

表1 基于测试参数的导弹质量状态等级划分

2 测试参数分析

导弹的质量状态通过电气属性测试参数体现，然而导弹“良好”、“较好”、“堪用”、“拟故障”4个状态等级之间不存在明确的划分，因此，就必须确定一个隶属度函数处理这种不确定性，以方便基层技术保障人员根据导弹的状态等级划分采取相应的维修保障措施。

2.1 归一化处理

电气属性测试结果反映了各性能参数的状态等级，越接近阈值标准值则质量状态等级越高，越接近阈值上下界则质量状态等级越低。由于测试参数包含电压值、电流值、温度、偏转角等多种测量参数，单位不一、阈值各异，因此，需要对各个测试参数进行归一化处理，用归一化结果对质量状态等级进行表示。归一化函数如(1)式所示：

(1)

式中：xi为第i个测试参数实测值；xs为标准值；xu为上阈值；xl为下阈值；k为测试参数变化对性能特征参数状态的影响程度，一般取1.

由归一化函数(1)式可知：当测试参数值接近标准值时，归一化值为0；当测试参数值接近上下阈值时，归一化值为1，即性能特征参数质量状态等级随着λi增大而降低。

2.2 确定隶属度函数

各性能参数质量状态之间不存在明确的边界，即导弹各性能参数质量状态的划分，因不存在从某一状态到相邻状态的明确划分而存在一定的模糊性。模糊集合通过隶属度函数表征。考虑到隶属度函数一般具有单峰性、对称性、均衡性等特征，选用(2)式所示的岭形分布隶属度函数确定各质量状态等级的隶属度，式中a为下限值，b为上限值。

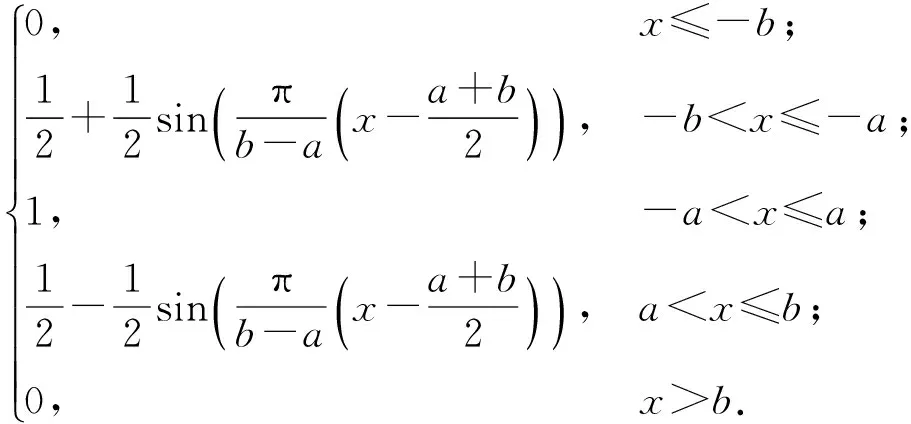
(2)

岭形分布隶属度函数具有主值区间宽、过渡带平缓的特征，具有良好的稳定性和控制敏感度，可以较好地表征导弹各质量状态之间的不确定性关系。

由于导弹质量状态划分为“良好”、“较好”、“堪用”、“拟故障”4个等级，相对比较详细，而(2)式的隶属度函数划分比较粗糙，无法充分表征各测试参数相对于质量状态等级的隶属度，且难以表达相邻状态之间的相关性。因此，结合导弹质量状态等级划分方式与退化规律，参考领域专家经验知识，对(2)式进行改进，改进后的隶属度函数曲线如图1所示。

从图1中可以看出：改进后的隶属度函数可以对相邻质量状态之间的不确定性进行量化表征；处于过渡区域的特征参数以不同的隶属度值同时隶属于两个相邻的质量状态等级，且两个状态的隶属度之和为1. 改进后，各个质量状态对应的隶属度函数分别为

(3)

(4)

(5)

(6)

μ1(λi)、μ2(λi)、μ3(λi)、μ4(λi)依次为第i个测试参数归一化值λi隶属于良好、较好、堪用、拟故障质量状态的隶属度函数，具有n个测试参数的模糊关系矩阵可表示为

(7)

3 基于BN的质量状态评估

确定导弹各性能特征参数的质量状态只是第一步，更重要的是如何融合各性能特征参数以确定整个导弹的质量状态等级。DS证据理论在数据融合方面具有一定的优势[13-15]，但是，当证据间存在严重冲突时，融合结果可能出现与实际情况矛盾的情况。相比于DS证据理论，BN模型[16-17]在融合各种不确定信息中优势更加明显，尤其是对于复杂大型系统，利用构建的拓扑网络可以进行正向与反向推理，并确定整个系统中的敏感元件与薄弱环节。

3.1 BN模型及建模方法

BN模型可以表示为BN=(G,θ)：网络结构G=(V,A)是一个有向无环图，节点V={V1,V2,…,Vn}(n≥1)，A是弧集合；网络参数θ描述CPT，用P(Vi|pa(Vi))表示。对于有向边(Vi,Vj)，Vi作为Vj的父节点，Vj作为Vi的子节点。Vi的父节点用pa(Vi)表示，而相应的非后代节点用A(Vi)表示。在给定pa(Vi)的条件下，Vi与A(Vi)条件独立：

P(Vi|pa(Vi),A(Vi))=P(Vi|pa(Vi)).

(8)

联合概率[18]为

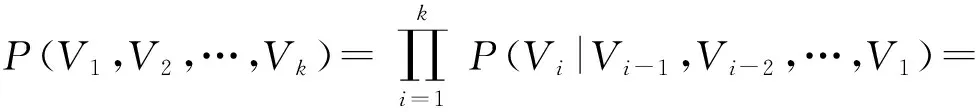
(9)

BN模型有3种构建方法[9,19]：1)利用专家经验知识，手动建立BN结构并确定CPT；2)利用数据库学习，自动建立BN结构和生成CPT；3)两阶段建模，即利用专家经验知识建立BN结构，借助数据库学习生成CPT. 大多数BN基于方法3构建，然而，利用统计信息进行CPT生成时容易出现多项式复杂程度的非确定性问题(NP)。

3.2 DS/AHP条件概率赋值

在故障树分析法向BN模型转化过程中，事件之间具有明确的串联、并联、2/3表决等逻辑关系，建立的BN为简单的二元状态或者三元状态，CPT可以通过串联和并联逻辑关系确定。随着二元状态向多状态拓展，对于复杂系统BN而言，节点之间为非确定性逻辑关系。BN参数学习过程复杂、新型装备数据缺乏，在进行质量状态评估或可靠性分析时，涉及专业知识、专家经验的随机变量引入，造成了一定程度上的不确定性。

考虑到各个专家在专业技术领域、知识构成、认知程度等方面的不同，应用DS/AHP对专家的不完善信息进行分析与表达，对片面信息进行融合，以确定多状态条件下的BN条件概率值。文献[14, 20]对DS证据理论进行了定义与介绍，对于识别框架Θ上的两个mass函数m1、m2可以根据Dempster规则合成：

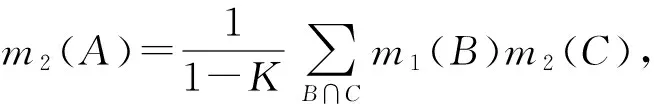
(10)

当数据信息缺乏时，引入DS/AHP方法对专家信息融合以降低认知不确定度，其判断标准如表2所示。相比于传统的AHP方法，DS/AHP在对备选方案进行评价时，不需要专家对所有方案两两比较，也不需要进行一致性检验，从而大大降低了工作量与计算量。并且专家可以只对确定的或者有把握的备选方案进行判断，对不确定或者没有把握的备选方案放弃判断。

表2 决策判断标准

在BN条件概率赋值确定过程中，假设有t个专家，分别记为e1,e2,…,et，从n个(c1,c2,…,cn)属性角度对条件概率组合的p个对象x1,x2,…,xp作出相对于识别框架Θ的重要性评判，建立如表3所示的知识矩阵。

表3 专家ei在属性cj下的知识矩阵

表3中：1表示与自身进行比较；0表示不进行比较；sk表示属性cj下的第k个焦元(k=1,2,…,r)；ak表示sk与识别框架Θ的比较指数(k=1，2，…，r)；pij表示专家ei在属性cj的权重。

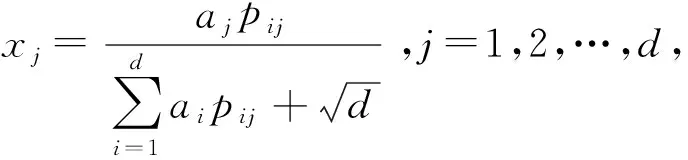
(11)

3.3 建模流程

导弹质量状态评估从性能特征参数出发，对于某个或者某些超出阈值范围的测试参数，直接判为故障；对于测试参数处于阈值范围内的性能特征参数按图2所示的流程进行处理：按(1)式进行归一化处理，将不同单位、不同属性的测试参数统一到同一个尺度下，按改进岭形隶属度函数(3)式～(6)式确定测试参数在不同状态下的隶属度，建立如(7)式所示的多个测试参数模糊关系矩阵；借助BN在处理不确定信息方面的优势，建立基于BN的多参数融合模型，应用DS/AHP方法确定模型结构参数，确定导弹所属的质量状态等级。由于测试“合格”的导弹各性能特征参数划分为良好、较好、堪用、拟故障4个等级，为方便起见，导弹质量状态也照此划分。

4 实例分析

某型导弹自2008年服役以来，每年定期检测一次，在此期间均未发生故障，即每次检测导弹质量为合格。为确定该型导弹的确切质量状态等级，运用本文设计的评估模型对2015年测试时的导弹状态进行评估，并采用横向对比与纵向对比进行模型验证。本文以某制导控制系统连续性单元测试为例进行质量状态评估，涉及4个性能特征参数：v1(连续性测试11.5 V电压)、v2(连续性测试11.5 V波纹)、v3(连续性测试23 V电压)、v4(连续性测试23 V波纹)。

4.1 性能特征参数分析

对该型导弹进行电气属性测试时，连续性单元测试数据如表4所示。应用(1)式对实测值、标准值、上下阈值进行归一化处理，并将结果分别代入(3) 式～(6)式获得性能特征参数分别隶属于良好、较好、堪用、拟故障4个质量状态等级的隶属度，如表4所示。

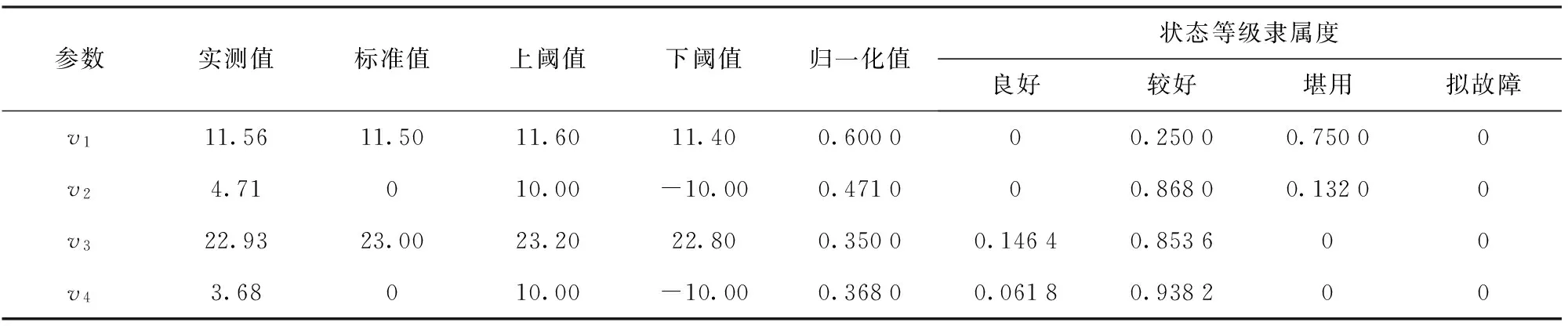
表4 连续性单元测试参数及其隶属度

4.2 BN模型构建

制导控制系统连续性测试4个性能参数中，v1和v2属于连续性单元11.5 V测试，v3和v4属于连续性单元23 V测试，以此构建BN模型，如图3所示。

用X表示连续性单元11.5 V测试的质量状态等级，用Y表示连续性单元23 V测试的质量状态等级，以T表示整个连续性单元测试的质量状态等级，同样，将X、Y、T划分为良好、较好、堪用、拟故障4个等级。根据4个节点隶属于各个状态的概率输入，在确定CPT之后即可进行整个连续性单元的质量状态等级评估。

4.3 条件概率赋值

为简便起见，假设在X节点中v1、v2同等重要，在节点Y中v3、v4同等重要，在节点T中X、Y同等重要，则有当两个节点分别处于相邻两个状态时，可以作等价替换而不影响整体评估的准确性和有效性。同时，假设X、Y、T具有同样的CPT，这3个节点处的基本概率分配(BPA)值由16个转化为10个，如表5所示，分别设为事件A～J.

表5 简化后的BPA值

咨询4名领域专家，依据表2的判断标准分别对10个事件相对于子节点所处质量状态的偏好程度建立知识矩阵，假设各专家权重分别为0.35、0.30、0.15、0.20. 以节点v1处于良好状态、v2处于较好状态为例，即以事件B为例，建立子节点X的知识矩阵，分别如表6～表9所示。

表6 以专家1偏好建立事件B知识矩阵B1

根据表6建立知识矩阵B1，求解det (B1-λI1)的最大特征值及相应的特征向量，I1为4×4单

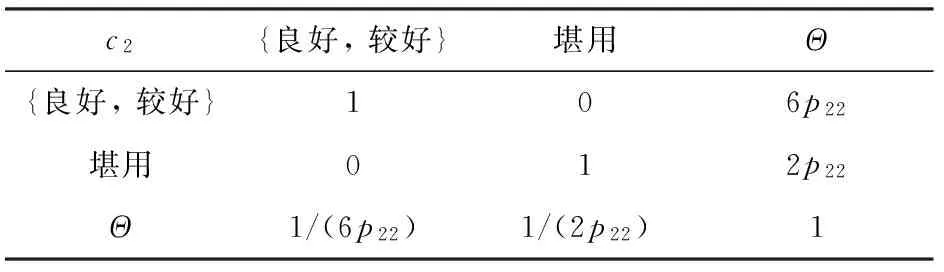
表7 以专家2偏好建立事件B知识矩阵B2

表8 以专家3偏好建立事件B知识矩阵B3

表9 以专家4偏好建立事件B知识矩阵B4

位向量，则有：m1(良好)=0.316 6,m1(较好)=0.263 9,m1(堪用)=0.158 3,m1(Θ)=0.261 2；m2(良好,较好)=0.471 9,m2(堪用)=0.157 3,m2(Θ)=0.370 8；m3(良好,较好)=0.344 3,m3(堪用,拟故障)=0.114 7,m3(Θ)=0.541 0；m4(良好)=0.332 0,m4(较好)=0.276 7,m4(Θ)=0.391 3.

类似地，可以求解知识矩阵B2～B4. 按照DS证据合成原则(10)式对信度函数进行合成，如表10所示。

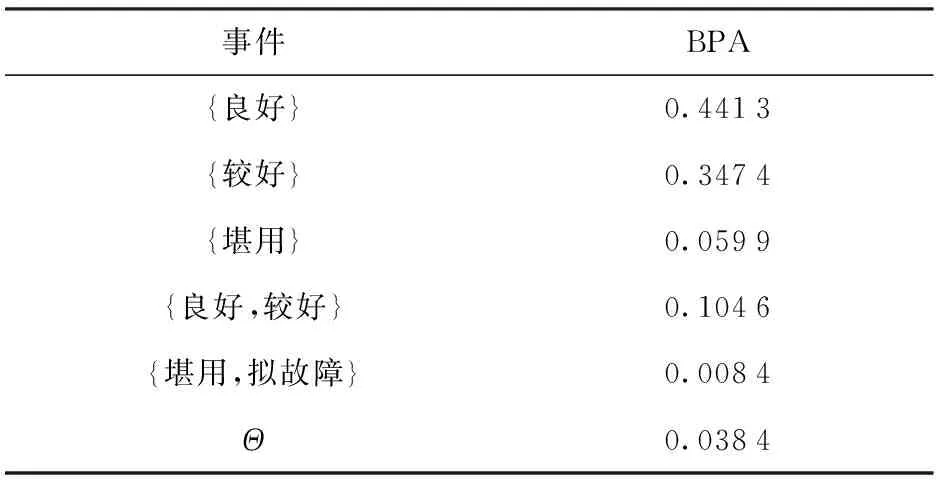
表10 事件B的BPA值

从表10可知，节点X状态为良好的可能性为0.441 3+0.104 6/2=0.493 6，为较好的可能性为0.347 4+0.104 6/2=0.399 7，为堪用的可能性为0.059 9+0.008 4/2=0.064 1，为拟故障的可能性为0.008 4/2=0.004 2，不确定度为0.038 4. 以此类推，可以求出其余9个事件的BPA值。

4.4 质量状态评估分析

根据v1、v2、v3、v4性能特征参数的状态隶属度，经BN模型推理，确定了节点X、Y的状态隶属度，进而确定连续性测试单元T隶属于{良好，较好，堪用，拟故障}的质量状态隶属度，如图4所示。连续性单元处于4个质量状态的隶属度依次为0.179 5、0.405 8、0.305 3、0.109 4，即连续性单元正处于较好状态，将逐渐向堪用状态过渡。

构建整枚导弹质量状态BN模型，利用所有的测试参数对导弹各子系统、子单元进行性能特征参数融合，从而确定所处的质量状态等级，有：m(良好)=0.115 3,m(较好)=0.397 2,m(堪用)=0.390 0,m(拟故障)=0.097 5，此时，导弹质量状态为较好，但是导弹处于堪用的隶属度非常接近于处于较好的隶属度，即导弹正处于从较好状态向堪用状态过渡的阶段，很快导弹就将进入堪用状态。

同时，利用2008年～2014年的测试数据进行质量状态等级评估可知，导弹的技术状态分别为良好、良好、良好、良好、较好、较好、较好，其质量状态呈逐步降级、退化趋势，这也正好验证了质量状态评估模型的合理性与可行性。在进行横向对比时，额外随机抽取9枚同一批次的该型导弹进行质量状态评估，其中：有1枚导弹无线电高度表110 m灵敏度测试参数超出阈值范围，判为故障；有1枚处于良好状态；有3枚处于较好状态；有3枚处于堪用状态；有1枚处于拟故障状态。即导弹质量状态处于良好、较好、堪用、拟故障和故障的概率分别为10%、40%、30%、10%、10%. 作为对比，随机抽取10枚同批次该型导弹进行质量状态评估，其中：有1枚导弹磁控管电流超出阈值范围，判为故障；有1枚处于良好状态；有4枚处于较好状态；有4枚处于堪用状态。即导弹质量状态处于良好、较好、堪用、拟故障和故障的概率分别为10%、40%、40%、0%、10%. 两个批次导弹的质量状态隶属度基本相同，较好状态与堪用状态的导弹数量基本一致，因此，本文构建的导弹质量状态评估模型合理、可信。

5 结论

针对“是非制”导弹质量状态评判方法过于粗放的弊端，本文提出了一种基于DS/AHP条件概率赋值的BN状态评估方法，对导弹质量状态等级进行了划分，主要结论有：

1)对现有的岭形隶属度函数进行了改进，充分考虑了处于过渡区域的性能特征参数值。

2)对于多状态非确定性逻辑节点，应用DS/AHP方法融合多位领域专家信息。就4名专家而言，应用该方法确定的CPT使得不确定度降低到了5%左右，随着专家数量的增加和判断标准的细化，由主观判断引起的认知不确定度将进一步降低。

3)利用BN的敏感性分析、重要度分析，通过反向推理可以确定在导弹质量状态评估中的薄弱环节，提高综合保障的精确性与准确性，为战备值班安排与维修保障决策制定提供科学的指导。

)

[1] 韩小孩，张耀辉，王少华，等. 基于关联维数分析的装备技术状态评估[J]. 系统工程与电子技术, 2016, 38(1): 110-115.

HAN Xiao-hai, ZHANG Yao-hui, WANG Shao-hua, et al. Equipment’s condition evaluation based on the analysis of correlation dimension[J]. Systems Engineering and Electronics, 2016, 38(1): 110-115.(in Chinese)

[2] 王少华，张耀辉，韩小孩. 基于多维特征参数的装备状态评估方法[J]. 系统工程与电子技术, 2014, 36(9): 1769-1775.

WANG Shao-hua, ZHANG Yao-hui, HAN Xiao-hai. Equipment condition evaluation based on multi-dimensional characteristics parameters[J]. Systems Engineering and Electronics, 2014, 36(9): 1769-1775.(in Chinese)

[3] 王京，李天梅，何华锋，等. 多源测试性综合评估数据等效折合模型与方法研究[J]. 兵工学报, 2017, 38(1): 151-159.

WANG Jing, LI Tian-mei, HE Hua-feng, et al. Research on multi-source data equivalent methods for testability integrated evaluation[J]. Acta Armamentarii, 2017, 38(1): 151-159.(in Chinese)

[4] 王亮，吕卫民，滕克难. 基于测试数据的长期贮存装备实时健康状态评估[J]. 系统工程与电子技术, 2013, 35(6): 1212-1217.

WANG Liang, LYU Wei-min, TENG Ke-nan. Real-time health condition assessment of long-term storage equipment based on testing data[J]. Systems Engineering and Electronics, 2013, 35(6): 1212-1217.(in Chinese)

[5] 丛林虎，徐廷学，董琪，等. 基于改进证据理论的导弹状态评估方法[J]. 系统工程与电子技术, 2016, 38(1): 70-76.

CONG Lin-hu, XU Ting-xue, DONG Qi, et al. Missile condition assessment method based on improved evidence theory[J]. System Engineering and Electronics, 2016, 38(1): 70-76.(in Chinese)

[6] 蒋金良，袁金晶，欧阳森. 基于改进隶属度函数的电能质量模糊综合评价[J]. 华南理工大学学报:自然科学版, 2012, 40(11): 107-112.

JIANG Jin-liang, YUAN Jin-jing, OUYANG Sen. Fuzzy comprehensive evaluation of power quality based on improved membership function[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(11): 107-112.(in Chinese)

[7] 周忠宝, 董豆豆, 周经伦. 贝叶斯网络在可靠性分析中的应用[J]. 系统工程理论与实践，2006，26(6): 95-100.

ZHOU Zhong-bao, DONG Dou-dou, ZHOU Jing-lun. Application of Bayesian network in reliability analysis[J]. System Engineering Theory & Practice, 2006, 26(6): 95-100.(in Chinese)

[8] 尹晓伟，钱文学，谢里阳. 基于贝叶斯网络的多状态系统可靠性建模与评估[J]. 机械工程学报, 2009, 45(2): 206-212.

YIN Xiao-wei, QIAN Wen-xue, XIE Li-yang. Multi-state system reliability mdeling and assessment based on Bayesian networks[J]. Journal of Mechanical Engineering, 2009, 45(2): 206-212.(in Chinese)

[9] Beynon M. DS/AHP method: a mathematical analysis, including an understanding of uncertainty[J]. European Journal of Operational Research, 2002, 140(1):148-164.

[10] 杜元伟，石方园，杨娜. 基于证据理论/层次分析法的贝叶斯网络建模方法[J]. 计算机应用, 2015, 35(1): 140-146.

DU Yuan-wei, SHI Fang-yuan, YANG Na. Construction method for Bayesian network based on Dempster-Shafer/analytic hierarchy process[J]. Journal of Computer Applications, 2015, 35(1):140-146.(in Chinese)

[11] Hua Z S, Gong B G, Xu X Y. A DS-AHP approach for multi-attribute decision making problem with incomplete information[J]. Expert Systems with Applications, 2008, 34(3):2221-2227.

[12] 姚爽，郭亚军，黄玮强. 基于证据距离的改进DS-AHP多属性群决策方法[J]. 控制与决策, 2010, 25(6): 894-898.

YAO Shuang, GUO Ya-jun, HUANG Wei-qiang. An improved method of aggregation in DS/AHP for multi-criteria group decision-making based on distance meaaasure[J]. Control and Decision, 2010, 25(6): 894-898.(in Chinese)

[13] 姜江. 证据网络模型及其推理算法[J]. 系统工程理论与实践, 2015, 35(4): 984-990.

JIANG Jiang. Evidential network model and reasoning approach[J]. System Engineering—Theory & Practice, 2015, 35(4): 984-990.(in Chinese)

[14] 孙伟超，李文海，李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J]. 北京航空航天大学学报, 2015, 41(10): 1902-1909.

SUN Wei-chao, LI Wen-hai, LI Wen-feng. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902-1909．(in Chinese)

[15] 黄影平. 贝叶斯网络发展及其应用综述[J]. 北京理工大学学报, 2013, 33(12): 1211-1219.

HUANG Ying-ping. Survey on Bayesian network development and application[J]. Transactions of Beijing Institude of Technology, 2013, 33(12): 1211-1219.(in Chinese)

[16] Wilson A G, Huzurbazar A V. Bayesian networks for multilevel system reliability[J]. Reliability Engineering & System Safety, 2007, 92(10):1413-1420.

[17] Simon C, Weber P, Evsukoff A. Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis[J]. Reliability Engineering & System Safety, 2008, 93(7):950-963.

[18] Piero B, Luca P, Lusine M, et al. Comparing the treatment of uncertainty in Bayesian networks and fuzzy expert systems used for a human reliability analysis application[J]. Reliability Engineering & System Safety, 2015，138: 176-193.

[19] Masegosa A R, Moral S. An interactive approach for Bayesian network learning using domain/expert knowledge[J]. International Journal of Approximate Reasoning, 2013, 54(8):1168-1181.

[20] 锁斌，曾超，程永生，等. 证据理论与贝叶斯网络相结合的可靠性分析方法[J]. 系统工程与电子技术, 2011, 33(10): 2343-2347.

SUO Bin, ZENG Chao, CHENG Yong-sheng, et al. Reliability analysis based on evidence theory and Bayesian network method[J]. Systems Engineering and Electronics, 2011, 33(10): 2343-2347.(in Chinese)