地磁场中磁目标的等效衰减磁矩定位方法

贾文抖， 林春生， 孙玉绘， 翟国君

(1.海军工程大学 兵器工程学院， 湖北 武汉 430033； 2.海军工程大学 导航工程系， 湖北 武汉 430033；3.海军海洋测绘研究所， 天津 300061)

0 引言

磁梯度张量具有能够有效克服地磁场的干扰、突出目标磁信号、更加全面地反映磁场细节等突出的优势，因此近年来基于磁梯度张量的探测技术逐步成为磁探测领域的研究热点，德国、美国、澳大利亚等国已相继研制出磁梯度张量探测系统，进行了大量的野外试验[1]，并逐步应用于军事和民用领域。

基于欧拉齐次方程的磁梯度张量定位方法是早期人们研究的一个重点，但该方法需要获取磁目标磁场中测量点上干净的目标三分量磁信号，这在地磁场环境中是难以实现的，实际应用效果也不够理想。磁梯度张量不变量是利用磁梯度张量数据计算出来的一些不随测量坐标系变化而变化的量，它反映了磁目标的磁场特征，不易受地磁场的干扰，因此适用于地磁场中磁目标的探测。另外，由于磁梯度张量不变量还具有不随测量坐标系的变化而改变的性质，适合于搭载在移动探测平台上。常见的不变量有磁梯度张量的特征值、迹、等效衰减磁矩μ等[2-3]。

江胜华等[4]依据磁梯度张量缩并理论对磁梯度张量的模Gt及参数k的空间分布特征进行了分析，结果显示Gt和参数k呈椭球形分布，并拟合得到k值分布的近似计算公式。陈谨飞等[5]建立了正六面体测量模型，利用磁梯度张量的模Gt进行磁目标定位，但由于参数k的存在使得定位结果有一定的偏差。若能对参数k的影响进行补偿，或者将其从磁梯度张量的模中完全消除掉，则可以进一步提高磁定位的准确性。Nara等[6]研究发现影响参数k分布变化的因素是磁矩与位置矢量之间的夹角，并给出了参数k随夹角变化的计算公式。吕俊伟等[2]研究发现参数k可以用磁梯度张量特征值的组合公式进行计算，从磁梯度张量的模Gt中消除参数k后，得到了一个仅与距离有关的不变量。该不变量就是等效衰减磁矩μ，而磁梯度张量的模Gt与等效衰减磁矩μ之间的比值就是参数k. 此外，Sui等[7]也对如何消除参数k带来的椭圆误差进行了研究，并进行了相应的实验，修正效果较好。实际上，关于不变量——等效衰减磁矩μ的研究在国外文献中早有出现，在1985年Wilson[8]就提出过与磁目标磁矩方向无关的不变量。Beiki等[9]研究发现当直线上的测点距离磁目标最近时，不变量等效衰减磁矩μ取得极大值这一特性。Clark[10]计算了磁梯度张量的3个特征值，发现可以用磁梯度张量的特征值直接计算出等效衰减磁矩μ，继而可以根据μ的分布规律确定磁目标的位置参数。Beiki等[11]进一步研究发现等效衰减磁矩μ同样满足欧拉齐次方程，并可以利用多点处μ的梯度值反演得到磁目标的位置。

在计算文献[2，4]中正六面体模型的六面体侧面磁梯度张量数据时，首先利用口字型布置的磁力仪测得的磁场数据近似计算磁梯度张量中的9个量，然后计算出相应的磁梯度张量不变量；计算目标源与测点的距离r时，根据上下2个侧面的磁梯度张量不变量与距离之间的比例关系，借助麦克劳林公式简化近似计算得到距离r的计算公式，本文称这种方法为方法1. 为了进一步降低上述计算误差，得到更精确的磁梯度张量信息和距离r，本文对方法1进行改进，在计算正六面侧面中心点的磁梯度张量中的分量时，采用坐标系旋转的方法将口字型布置的磁力仪阵列变成十字型测量阵列，相比方法1，所用到的磁力仪数目由4减少到2. 由于正六面体中心点既不位于正六面体中某个正方形中心点也不位于十字型交叉点，该中心点的磁梯度张量既不能利用口字型磁力仪阵列也不能利用十字型磁力仪阵列差分计算得到。为此根据全微分概念，提出一种微分求解方法，利用正六面体上下对角磁力仪测量的磁梯度数据建立微分方程组，求解计算磁梯度张量中的9个元素量，解决了正六面体中心点磁梯度张量难以计算的问题。在计算目标源与测点的距离r时，直接利用等效衰减磁矩μ的梯度公式推导得到r，消除了方法1中借助麦克劳林公式简化计算带来的误差。最后根据μ的圆周分布特征进行磁目标位置参数的反演，实现磁目标的定位。

1 基于等效衰减磁矩的定位方法

1.1 磁梯度张量特征值的旋转不变特性

将磁偶极子视为研究对象，以磁偶极子位置为原点(0, 0, 0)建立直角坐标系Oxyz，磁偶极子的磁矩M=(mx,my,mz)，位置矢量为r=(x,y,z)的测量点Q处磁感应强度为

(1)

B的三分量形式为

(2)

磁梯度张量G为磁场三分量在空间x、y、z方向上的导数，其形式为

(3)

式中：

(4)

下标i、j表示x、y、z方向中的任意2个，δij是克罗内克函数，当i=j时δij=1，当i≠j时δij=0，ri、rj表示距离矢量r=(x,y,z)中的任意两个分量。

根据特征方程det (G-λI)=0(I是与G维数相同的单位对角阵，λ是待求的磁梯度张量特征值)，计算得到G的特征值为

(5)

式中：

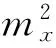
假设坐标系Oxyz绕x轴旋转角后得到坐标系Oxαyαzα. 在坐标系Oxαyαzα中，测量点Q的坐标、磁矩M可分别表示为

(6)

(7)

将(6)式、(7)式代入(5)式，计算得到坐标系Oxαyαzα中测量点Q处磁梯度张量对应的特征值为

(8)

由(8)式可知，磁偶极子上坐标系Oxyz绕x轴旋转前后磁梯度张量G的特征值不变。当坐标系绕y轴、z轴旋转时，同样可得磁梯度张量特征值不随测量坐标系的旋转而变化。由于位于磁偶极子处的任意直角坐标系都可以由坐标系Oxyz绕经x轴、y轴、z轴旋转得到，根据以上分析可知，当固定了测量点与磁目标点的相对位置，同一测量点的磁梯度张量特征值在不同直角坐标系中都是相等的。因此，磁梯度张量的特征值是磁梯度张量的旋转不变量。

1.2 等效衰减磁矩的定位原理

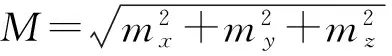
(9)

式中：

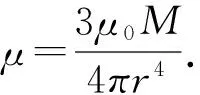
(10)

根据特征方程

det (G-λI)=-(μcosβ-λ)[(2μcosβ+
λ)(μcosβ-λ)+μ2sin2β]=0,

求得特征值为

(11)

由(11)式可得

(12)

当矢量r与磁矩M同向(β=0)或反向(β=180)时G退化为对角矩阵，对角线上的元素即为特征值，磁梯度张量的特征值与等效衰减磁矩之间的关系同样满足(12)式。由于特征值是磁梯度张量的不变量，因此μ也是磁梯度张量的不变量，且与位置矢量r的模的4次方呈反比。

(13)

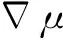
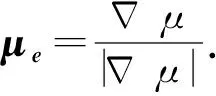
(14)

根据(13)式可得，测量点Q与磁偶极子之间的距离为

(15)

则位置矢量r为

r=-rμe.

(16)

2 正六面体定位模型

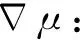
(17)

以计算x轴正向对应面中心的μx-为例，磁力仪S1、S2、S3和S4测量的磁感应强度分别为

(18)

由第1节的分析可知，μ不随计算坐标系的变化而变化。将磁力仪S1、S2、S3和S4测得的3个分量数据对应到坐标系Ox45°y45°z45°中(见图3)，坐标系Ox45°y45°z45°由坐标系Oxyz绕x轴顺时针旋转45°得到。

测量数据由坐标系Oxyz对应到坐标系Ox45°y45°z45°中的转换公式为

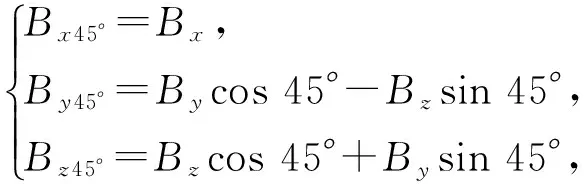
(19)

式中：Bx、By、Bz为坐标系Oxyz中磁力仪直接测得磁场的3个分量；Bx45°、By45°、Bz45°为对应到坐标系Ox45°y45°z45°中的3个分量。

在坐标系Ox45°y45°z45°中，直接利用差分方法计算磁梯度张量：

G45°=

计算正六面体中心点P处的等效衰减磁矩μP时，由于正六面体中心点处的磁梯度张量无法按照差分方法计算得到，在此利用全微分的概念，建立微分方程组间接求解磁梯度张量各分量[12]。将图2中的8个磁力仪按交叉线分成4组：S1和S8、S2和S7、S3和S6、S4和S5. 这4组磁力仪各自的连线均过正六面体中心点P. 以磁力仪S1和S8这一组为例，磁力仪S1和S8的测量数据差值为

ΔB81=(ΔB81x,ΔB81y,ΔB81z)=

(B8x-B1x,B8y-B1y,B8z-B1z).

(20)

根据全微分的概念，结合S1、S8的空间位置，有

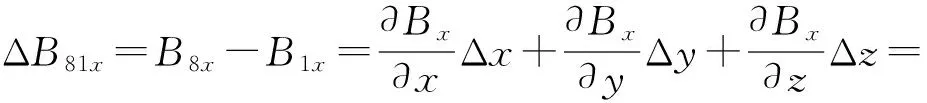
(21)

结合其他3组磁力仪数据，则有方程组：

(22)

求方程组(22)式即可得到Gxx、Gxy和Gxz. 类似地，利用ΔBy和ΔBz的全微分表达式，可计算得到Gyx、Gyy、Gyz、Gzx、Gzy和Gzz. 得到正六面体中心点P处的磁梯度张量G后，可计算出等效衰减磁矩μP.

3 仿真分析

仿真条件设置为磁偶极子磁矩M=(3 000 A·m2，3 300 A·m2，4 200 A·m2)，磁目标的真实位置坐标r=(-4 m，-6 m，-11 m)，计算得到的位置参数用rP表示，位置参数的相对误差为

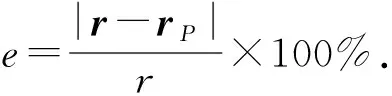
下面分析地磁场、磁梯度测量噪声、正六面体基线以及磁力仪测量精度等因素对位置参数反演结果的影响，并与方法1的反演结果进行比较。

3.1 地磁场对定位结果的影响

假设研究环境中地磁场大小为50 000 nT，地磁场梯度0.02 nT/m[13]，地磁倾角I=42°，磁偏角T=3°(设北偏东为正)。正六面体模型中的坐标系x轴正向朝东，y轴正向朝北，z轴正向朝上。测量数据分两种：一组数据中包含地磁场；一组数据中不含地磁场。根据设定的磁目标参数，利用仿真的两组数据计算磁目标的位置参数，计算结果见表1.

表1 有无地磁场时的定位结果

从表1中的计算结果可以看出，以磁偶极子作为磁目标，利用本文方法进行磁目标位置参数的反演计算时，地磁场对定位结果的影响很微弱，在应用中地磁场的影响完全可以忽略。

3.2 磁梯度噪声对定位结果的影响

在测量过程中，由于周围的磁场环境比较复杂，各种设备及人为干扰难以避免，且各磁力仪之间还存在匹配误差，使得测量的目标磁场梯度信号中不可避免地包含一定的磁干扰量，测得的磁梯度信号不纯净。本文将这些磁干扰等效为磁梯度噪声，添加到目标磁信号测量数据中，磁梯度测量噪声对定位结果的影响见图4.

图4中蓝线是磁梯度测量噪声水平为0.353 6 nT/m、随机进行100次计算得到的定位误差曲线，黑线是磁梯度测量噪声水平为0.707 2 nT/m、随机进行100次计算得到的定位误差曲线。由图4可见：磁梯度噪声水平为0.353 6 nT/m时，定位误差不超过1 m，大部分误差在0.5 m以内；磁梯度噪声为0.707 2 nT/m时，定位误差几乎全在1.5 m以内，大部分不超过1 m. 由于初始设置磁目标的磁矩不大，在测量点上目标信号的磁梯度大小约为几十纳特斯拉每米，相当于测量信号中的磁梯度噪声不超过目标信号强度的10%，定位相对误差也基本维持在10%以内。

3.3 基线长度对定位结果的影响

根据磁梯度张量G45°的表达式可知，采用差分替代微分的方法计算磁梯度张量时，基线长度会影响G45°的计算结果，并最终影响位置参数的反演结果。定位误差随基线长度变化的曲线见图5.

从图5可以看出，定位误差随正六面体边长基线的增加而变大。主要是因为计算六面体侧面的磁梯度张量时采用的是差分计算方法，与磁梯度张量的理论值之间存在一定的偏差，差分基线越长，偏差越大，定位误差也越大。在本节设置的条件下，当边长基线不超过1.5 m时，定位误差在0.7 m以内。

3.4 磁力仪测量精度对定位结果的影响

当磁力仪测量精度不同时，从表2中的定位结果可以看出，测量精度从0.01～1 nT逐渐降低时定位误差逐渐加大，当磁力仪的测量精度为1 nT时，定位误差在1.4 m左右，相对误差约为11%.

表2 不同测量精度时的定位误差

3.5 本文方法与方法1的比较

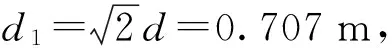
表3 本文方法与方法1的计算结果比较

由表3可知，在磁力仪测量精度相同情况下，利用本文方法反演计算得到的位置参数与真实的位置参数更加接近，定位误差为0.101 m，相对误差为0.77%. 利用方法1反演计算磁目标位置参数时，定位误差为0.418 m，相对误差为3.18%. 由此可见，本文方法的定位精度高于方法1. 另外，在磁梯度计算基线相等的情况下，本文正六面体模型的空间体积仅为方法1中模型体积的35.3%，显著降低了模型所占的空间体积。

4 结论

本文研究了在地磁场中利用磁目标的等效衰减磁矩信息实现磁目标定位的方法。通过计算分析了等效衰减磁矩μ不随测量坐标系的改变而变化的特征。根据这一特征，利用了坐标系旋转的方法将口字型布置的磁力仪阵列转变成十字型，在差分基线相等的情况下使正六面体的边长缩减为原来的0.707倍。利用求解全微分方程组的方法计算得到正六面体中心点的磁梯度张量，解决了正六面体中心点磁梯度张量难以计算的问题。对磁目标位置参数进行了反演，结果表明在地磁场中利用等效衰减磁矩的定位方法可实现对磁目标的有效定位。与之前的计算方法相比，在计算磁梯度的差分基线相等的情况下，本文方法正六面体模型的体积减小了64.7%，且定位效果更好。

)

[1] 于振涛，吕俊伟，毕波，等．四面体磁梯度张量系统的载体磁干扰补偿方法[J]．物理学报，2014，63(11)：110702-1-110702-6．

YU Zhen-tao, LYU Jun-wei, BI Bo, et al. A vehicle magnetic noise compensation method for the tetrahedron magnetic gradiometer[J]. Acta Physica Sinica，2014, 63(11): 110702-1-110702-6. (in Chinese)

[2] 吕俊伟，迟铖，于振涛，等．磁梯度张量不变量的椭圆误差消除方法研究[J]．物理学报，2015，64(19)：190701-1-190701-8．

LYU Jun-wei, CHI Cheng, YU Zhen-tao, et al. Research on the asphericity error elimination of the invariant of magnetic gradient tensor[J]. Acta Physica Sinica，2015, 64(19): 190701-1-190701-8. (in Chinese)

[3] 万成彪，潘孟春，张琦，等. 基于张量特征值和特征向量的磁性目标定位[J]. 吉林大学学报：工学版，2017，47(2)：655-660．

WAN Cheng-biao, PAN Meng-chun, ZHANG Qi, et al. Magnetic object location with eigenvalue and eigenvector of tensor[J]. Journal of Jilin University: Engineering and Technology Edition, 2017, 47(2):655-660. (in Chinese)

[4] 江胜华，申宇，褚玉程．基于磁偶极子的磁场梯度张量缩并的试验验证及相关参数确定[J]．中国惯性技术学报，2015，23(1)：103-106．

JIANG Sheng-hua, SHEN Yu, CHU Yu-cheng. Experimental verification and related parameter's determination for magnetic gradient tensor contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 103-106. (in Chinese)

[5] 陈谨飞，张琦，潘孟春，等．基于正六面体结构测量阵列的磁异常定位技术研究[J]．传感技术学报，2012，25(8)：1088-1092．

CHEN Jin-fei, ZHANG Qi, PAN Meng-chun, et al. Research on geomagnetic anomaly localization based on cubic measurement array[J]. Chinese Journal of Sensors and Actuators, 2012, 25(8): 1088-1092. (in Chinese)

[6] Nara T, Ito W. Moore-penrose generalized inverse of the gradient tensor in Euler's equation for locating a magnetic dipole[J]. Journal of Applied Physics, 2014, 115(17): 17E504-1-17E504-3.

[7] Sui Y Y, Li G, Wang S L, et al. Asphericity errors correction of magnetic gradient tensor invariants method for magnetic dipole localization[J]. IEEE Transactions on Magnetics, 2012, 48(12):4701-4706.

[8] Wilson H. Analysis of the magnetic gradient tensor[R]. Canada: Defence Research Establishment Pacific, 1985: 5-13.

[9] Beiki M, Keating P, Clark D. Depth estimation of magnetic and gravity sources using normalized source strength calculated from gradient tensor[C]∥2012 SEG Annual Meeting.Las Vegas, CA，US: The Society of Exploration Geophysicists, 2012: 996.

[10] Clark D A. New methods for interpretation of magnetic vector and gradient tensor data I: eigenvector analysis and the normalised source strength[J]. Exploration Geophysics, 2012, 43(4):267-282.

[11] Beiki M, Clark D A, Austin J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics, 2012, 77(6):23-37.

[12] 贾文抖，林春生，孙玉绘，等．基于单个磁梯度计的磁目标定位方法研究[J]．兵工学报，2017，38(8)：1572-1577．

JIA Wen-dou, LIN Chun-sheng, SUN Yu-hui, et al. Research on magnetic target location method based on a single magnetic gradiometer[J]. Acta Armamentarii, 2017, 38(8): 1572-1577. (in Chinese)

[13] 张光，张英堂，李志宁，等．载体平动条件下的磁梯度张量定位方法[J]．华中科技大学学报：自然科学版，2013，41(1)：21-24．

ZHANG Guang, ZHANG Ying-tang, LI Zhi-ning, et al. Localizing method of magnetic field gradient tensor under carriers moving parallelly[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2013, 41(1): 21-24. (in Chinese)