云环境下基于L-BFGS的协同过滤算法
金 淳,何世福
(大连理工大学 管理与经济学部 系统工程研究所,辽宁 大连 116024)
0 引 言
为解决数据量的快速增长带来严峻的数据稀疏性问题[1],一些研究通过填充未评分项目值[2,3]、SVD[4-6]等矩阵分解和聚类[7-9]等方法对协同过滤算法改进,但存在填充后数据量极大增加导致的计算资源消耗,或缩减评分数据集带来评分预测精度降低的问题。因子分解机模型[10](简称FM模型)使用矩阵分解的思想,将多项式参数分解成为两个辅助向量,考虑了特征组合问题,对稀疏数据有良好学习能力和较高的预测精度。为解决数据维度、用户和商品特征数目的增加带来推荐算法可扩展性问题,目前主要使用数据集缩减[11]、增量更新[12,13]和矩阵分解[14]等方法来提取较小的数据集,但这些方法在海量数据情况下的迭代次数增多、计算矩阵的指数级增长,计算效率较低。L-BFGS(limited-memory BFGS)[15-17]是拟牛顿法的一种,核心思想为存储和使用最近的若干次迭代计算的向量序列来构造Hessian矩阵的近似矩阵,具有收敛速度快和占用计算空间低等特点。而FM使用传统方法进行参数训练收敛速度较慢,使用L-BFGS算法进行参数训练可以弥补此缺点,使算法具有良好的可扩展性。
综上,本文提出基于L-BFGS优化的协同过滤推荐算法(L-BFGS-CF)。该算法使用FM模型进行评分预测,L-BFGS算法作为FM模型训练方法。本研究试图为解决云环境数据极度稀疏情况下的协同过滤算法计算效率及可扩展性提出新思路。
1 问题描述及方法分析
1.1 问题描述
推荐系统根据已有的用户特征、行为(如查看、购买、评分)信息和商品特征信息,对已有商品进行评分预测,按预测的评分结果排序得到推荐列表,将相应的商品推荐给用户。在推荐系统中,一般产生如下数据矩阵:用户评分矩阵(User-Item评分矩阵)、用户特征矩阵和商品特征矩阵。设User-Item评分矩阵R中包含m个用户U={Ui|i=1,2,…,m}和n个商品I={Ij|j=1,2,…,n},那么R可以用一个m×n矩阵表示,如式(1)所示
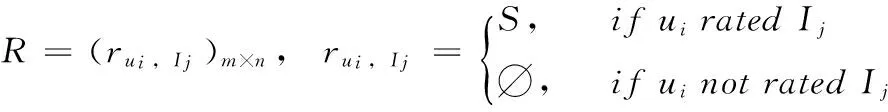
(1)
其中,评分r描述了用户对不同商品的偏好程度,分数越高表示用户越喜欢该商品;若r=∅表示该用户ui没有对商品Ij评分,具体评分矩阵为R=[r1,1,…,r1,n;r2,1,…,r2,n;…;rm,1,…,rm,n]。
用户特征表包含m个用户和p个特征FU={FU,k|k=1,2,…,p},如用户的年龄、职业等。商品特征一般包含n个商品和q个特征FI={FI,l|l=1,2,…,q},如商品的类型、品牌等特征。在协同过滤推荐时考虑用户和商品的特征组合问题能取得更好的推荐质量。
1.2 现有方法及分析
协同过滤技术是根据用户对商品或信息的行为偏好,发现用户、商品或内容之间的相关性进行推荐,主要技术包括:基于用户(user-CF)、基于商品(item-CF)和基于模型(model-CF)的协同过滤算法。主要技术的假设与定义见文献[1]。
1.2.1 相似性度量方法
基于用户或商品的协同过滤无需获取用户或商品特征,只依赖于现有评分数据和相似度计算方法对评分进行预测,所以User-Item评分矩阵越密集,预测精度越高。协同过滤中的相似度计算方法一般使用Jaccard相似系数、余弦相似度和Pearson相关系数。设用户u和v之间的相似度为Sim(u,v),3种相似度计算方式如式(2)、式(3)、式(4)所示[18]
(2)
(3)
(4)

User-CF或Item-CF方法的核心在于通过相似性计算找到用户或商品的最近邻居。但是,在评分矩阵极度稀疏的情况下,两个用户共有评分集合I(u,v)很小,通常只有几个少数的商品。数据稀疏性使该方法无法得到准确的用户或商品相似度,使得计算出的目标商品或用户的最近邻居不准确,导致算法精度不高。
1.2.2 基于模型的协同过滤
由于相似性度量方法的缺点,一些学者使用Model-CF进行研究。主要基于User-Item评分矩阵训练出推荐模型,对未评分商品进行评分预测。其中协同过滤的经典算法Slo-peOne算法基于这样一种假设:两个商品的偏好值之间存在着某种线性关系,可以通过线性函数Y=mX+b来描述,即通过商品X的偏好值对Y的偏好值进行预测[9]。如式(5)所示
(5)
其中,I(u,v)为用户u和v共同评分的项目集合,r代表用户评分。
该算法简单、快速、容易实现,但仅通过线性回归计算商品间的评分差异对评分进行预测,没有考虑商品间共同评分的用户数目,导致算法精度不高。
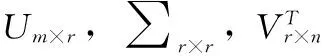
(6)
(7)

在云环境的大数据量情况下,该算法的r值选取存在一定的困难,选取过小会导致失去评分矩阵中的重要信息和结构;选取过大达不到降维的目的且容易导致训练数据过拟合问题,严重影响算法精度。
上述传统基于模型的协同过滤方法通过填充评分矩阵导致数据量急剧增长,且需要更多的迭代次数,使其计算效率和算法可扩展性不高,难以适应云环境下快速增长的数据量、数据高维化和算法可扩展性要求。
2 基于L-BFGS的协同过滤算法
2.1 基本思路
本算法属于基于模型的协同过滤算法。算法改进思路为:使用L-BFGS优化算法对FM模型进行训练,再使用FM模型进行评分预测,力求从精度和效率两方面对协同过滤模型进行提升。在云环境下,User-Item评分数据维度越来越高的同时也变得越来越稀疏,使用FM模型对极度稀疏数据的良好学习能力,提高对用户评分的预测精度。L-BFGS优化算法用来训练FM模型在精度和效率上都有较好的表现。结合Spark分布式计算框架的特性,使本算法能够适应云环境下的协同过滤推荐。
2.2 FM模型
本算法使用FM模型进行用户对商品的评分预测以提高算法计算效率和精度。FM模型引进辅助向量对多项式模型(本文只考虑二阶多项式模型)的二次项参数进行估计,旨在解决在数据稀疏情况下训练多项式模型参数的问题[10]。
多项式模型的特征xi和xj组合一般用xixj表示,即xi和xj都不为零时,组合特征xixj才有意义。多项式模型二阶方程为式(8)
(8)
其中,F代表样本的特征数量,xi是第i个特征的值,w0、wi、wij是模型参数。每个二次项参数wij需要大量xi和xj都非零的样本进行训练,但实际推荐系统中数据稀疏度非常大,可供模型训练的样本极少,导致参数wij不准确进而严重影响模型的精度。
FM模型基于矩阵分解的思路,将式(8)中的二次项参数wij组成一个对称矩阵W,使用矩阵分解方法可分解为W=VTV,V的第j列为第j维特征的隐向量,则二次项参数可以表示为wij=vi,vj。因此,FM模型方程如式(9)所示

(9)
其中,vi是第i维特征的隐向量,vi,vj代表向量点积,隐向量长度为K(K≪F)。在式(9)中,二次项的参数数量为K×F个,相比多项式模型的二次项参数数量F(F+1)/2要大大减少。而由于将wij分解为两个隐向量的点积vi,vj,所以特征组合xkxi和xixj的系数vk,vi和vi,vj有了共同项vi而不再相互独立。即所有包含xi的非零特征组合的样本都可以用来训练vi,从而极大减轻数据稀疏性的影响。
对式(9)的二次项进行化简,可将模型改写为式(10)
(10)
化简后的FM模型时间复杂度从O(KF2)优化到了O(KF),极大提高模型计算效率。
使用FM模型进行预测时,考虑L2正则的优化目标函数,通常取式(11)

(11)
Rendle[10]使用了随机梯度下降(SGD)、交替最小二乘法(ALS)和马尔可夫链蒙特卡罗法(MCMC)3种学习算法来进行参数学习,也有较好的预测精度。但是在数据量剧增的情形下,上述算法需要的迭代次数和计算资源消耗较高,所以本文使用更适合实际业务的大规模优化算法:L-BFGS算法,来对FM模型进行参数训练。
2.3 L-BFGS优化算法

在L-BFGS算法中,迭代格式为式(12)
xk+1=xk+αkPk
(12)
式中,αk为步长,Pk为搜索方向,Pk的计算公式为式(13)
Pk=-Hk▽f(xk)
(13)
对L-BFGS算法过程,对sk和yk作如下定义
sk=xk+1-xk
(14)
yk=gk+1-gk
(15)
(16)
其中,gk≡▽f(xk),上述式(14)和式(15)一维数组即是需要保存的每次迭代的曲率信息。
结合FM模型,L-BFGS算法流程如下:
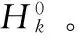
(17)
(18)
其中,τk为比例系数,E为单位矩阵。
步骤2 使用式(12)沿搜索方向找到下一个迭代点;
步骤3 根据Armijo-Goldstein准则和FM传入参数允许偏差值ε判断算法是否停止;
步骤4 如果|▽f(xk)|≥ε,使用式(13)更新搜索方向Pk;
步骤5 将训练得到的参数w0、一次项参数矩阵W和二次项隐向量V返回到FM模型。
L-BFGS算法利用最近一次保存的曲率信息来估计实际Hassian矩阵的近似矩阵,这使得当前步的搜索方向较为理想,收敛速度较快,同时实际工程中,一般设置步长αk=1,在大多数情况下都是满足的,节省了步长搜索时间,提高算法效率。
2.4 L-BFGS-CF算法流程
综上,本文提出的L-BFGS-CF算法采用L-BFGS训练FM模型参数,算法流程如图1所示。L-BFGS-CF算法的详细步骤如下:
输入:数据集R,迭代次数T′,隐向量v维度,正则化系数λ,允许偏差ε
输出:填充后的预测评分矩阵R′
步骤1 初始化Spark实例配置SparkContext(),读取Spark环境配置;
步骤2 使用FM模型对数据集R进行格式化转换并按8∶2比例随机划分为训练集Rtrain和测试集Rtest;
步骤3 将转换后的训练集Rtrain、模型参数传递给L-BFGS算法;
步骤4 初始化L-BFGS参数,选择初始点x0和需要存储的迭代次数T′;

步骤6 根据式(12)进行迭代计算;
步骤7 如果|▽f(xk)|≥ε,根据式(13)计算搜索方向Pk,返回步骤6;
步骤8 如果|▽f(xk)|≤ε,返回训练参数w0、W和V给FM模型;
步骤9 用式(10)对测试集Rtest商品进行评分预测,填充评分矩阵R′。

图1 L-BFGS-CF算法流程
3 实验设计及结果分析
3.1 实验设计
为验证L-BFGS-CF改进后的预测效果,采用4组不同数据量的数据集进行实验。选取SVD++,KNN-100和基于聚类(记为Cluster)的3种协同过滤算法对比分析,验证L-BFGS-CF的精度;其次增加实验数据的特征个数,分析使用L-BFGS-CF算法数据特征数量与精度的关系;最后,使用不同迭代次数对L-BFGS-CF进行实验,分析算法收敛速度。
3.1.1 实验环境
实验环境为VMware搭建的Spark高可用(HA)集群,包含3个节点:主节点为Master,子节点分别为Slave01和Slave02。安装内存16 G,处理器为四核Intel Core i5 2.6.0 GHz,软件环境为CentOS-6.7,Hadoop-2.5.0-cdh5.3.6,Spark-1.6.1-cdh5.3.6,Scala-2.10.4,jdk-1.7.67。内存及各组件分配见表1。

表1 实验节点资源分配情况
3.1.2 实验数据集
实验数据集使用MovieLens(http://grouplens.org/datasets/movielens/)、NetFlix Prize(http://www.netflixprize.com/)及天池竞赛(https://tianchi.shuju.aliyun.com/datalab/index.htm)数据集。MovieLens是由GroupLens Research从MovieLens站点提供的评分数据进行收集整理,此数据被广泛用于研究协同过滤的实验数据,分别选取数据量大小10万和100万的数据集:MovieLens-100K,MovieLens-1M。同时,为了验证模型对不同数据集的适应性,采用天池竞赛IJCAI-15 Dataset进行实验。该数据集包含天猫40多万用户的5000万条购买商品记录,从中抽取1000万条有效数据记为TMALL-10M,用于预测用户再次购买同一商家商品的可能性。NetFlix数据集包含17万多用户的19亿条评分记录,由于实验环境限制,本文从中选取1%的评分数据进行实验,记为NetFlix-100M。
表2统计了各组数据集的特征数量情况,包括评分数量(rating),用户数量(user),商品数量(item),以及数据稀疏度(sparsity),数据稀疏度通过式(19)计算。此外,用户性别、用户年龄及用户职业等用户特征,商品类型及标签等商品特征可以直接从上述数据集中获取
(19)

表2 实验数据集特征
实验从每个数据集中随机选取80%作为训练集,剩余20%作为测试集。通过划分不同比例进行实验,结果表明训练集和测试集的比例划分对L-BFGS-CF的影响甚微。
3.1.3 评判度量指标
推荐系统性能的评判度量指标通常使用均方根误差(RMSE)和平均绝对误差(MAE)。其中,RMSE作为NetFlix Prize赛事的标准度量指标;MAE广泛使用于推荐系统预测精度的评判标准。RMSE和MAE越低,表示推荐系统的预测精度越高。各指标计算如式(20)和式(21)所示[1]
(20)
(21)
3.2 结果与分析
3.2.1 不同数据量下4种算法精度对比
为方便比较,选取迭代次数为100次和特征数量为4个的情况下进行实验对比,结果如图2和图3所示。相比较小的数据集,NetFlix-100M的精度提升最为明显。

图2 不同数据量大小情况4种算法的RMSE值对比
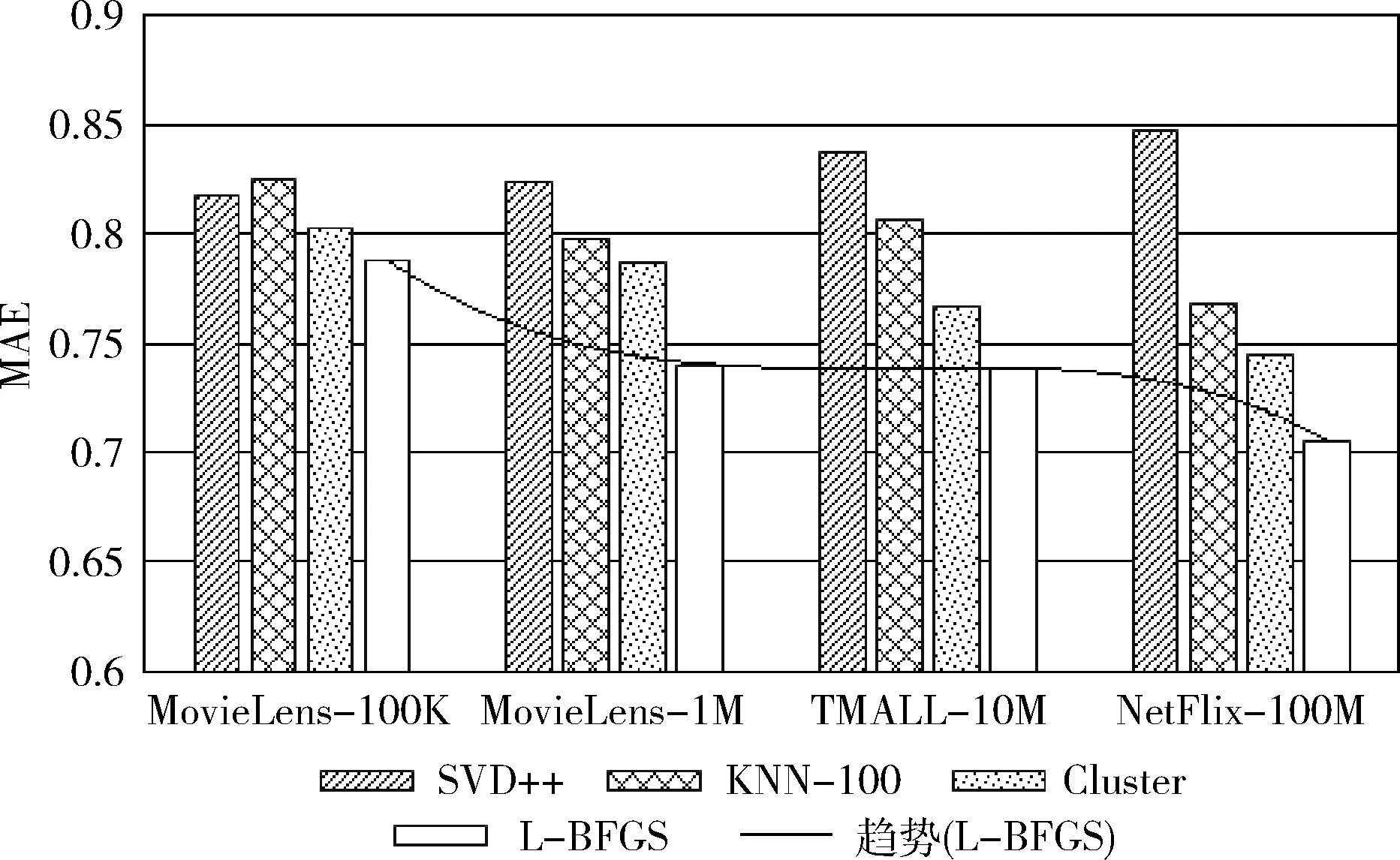
图3 不同数据量大小情况4种算法的MAE值对比
(1)L-BFGS-CF与SVD++相比,RMSE和MAE值分别降低0.198和0.142。SVD++属于矩阵分解的一种,由于是随机填充User-Item评分矩阵,大量增加了数据量及算法复杂度,同时数据填充造成数据失真,从而使预测精度下降,这在数据量越大的时候变得更加明显。
(2)与KNN-100相比,RMSE和MAE值分别降低0.085和0.063。KNN-100算法虽然无需训练模型,但对于样本不平衡的数据误差比较大,且算法计算量大,在数据量很大时需要耗用大量的内存。
(3)与Cluster相比,RMSE和MAE值分别降低0.056和0.04。Cluster方法由于聚类中心往往是随机选择的,存在聚类结果不稳定的问题,同时算法复杂度高,在不断地迭代过程中,保存的计算矩阵占用大量的内存和CPU时间,在精度和速率上都有所欠缺。
在不同大小的数据对比中,L-BFGS-CF算法均有最低的RMSE和MAE值,具有良好的预测精度。而对于TMALL-10M的数据集,由于预测结果为布尔类型,算法精度相比预测评分值的其它数据要低。
3.2.2 特征数量对L-BFGS-CF精度的影响
选取MovieLens-1M数据集考查L-BFGS-CF迭代次数T和特征数量F的关系,分析对算法精度的影响,结果如图4和图5所示。随着L-BFGS-CF算法迭代次数的增加,3种特征数量的情况下算法MAE和RMSE值都逐渐减少;而随着特征数量的增加,L-BFGS-CF算法的精度随之提升,但需要更大的迭代次数才能达到较为理想的精度。
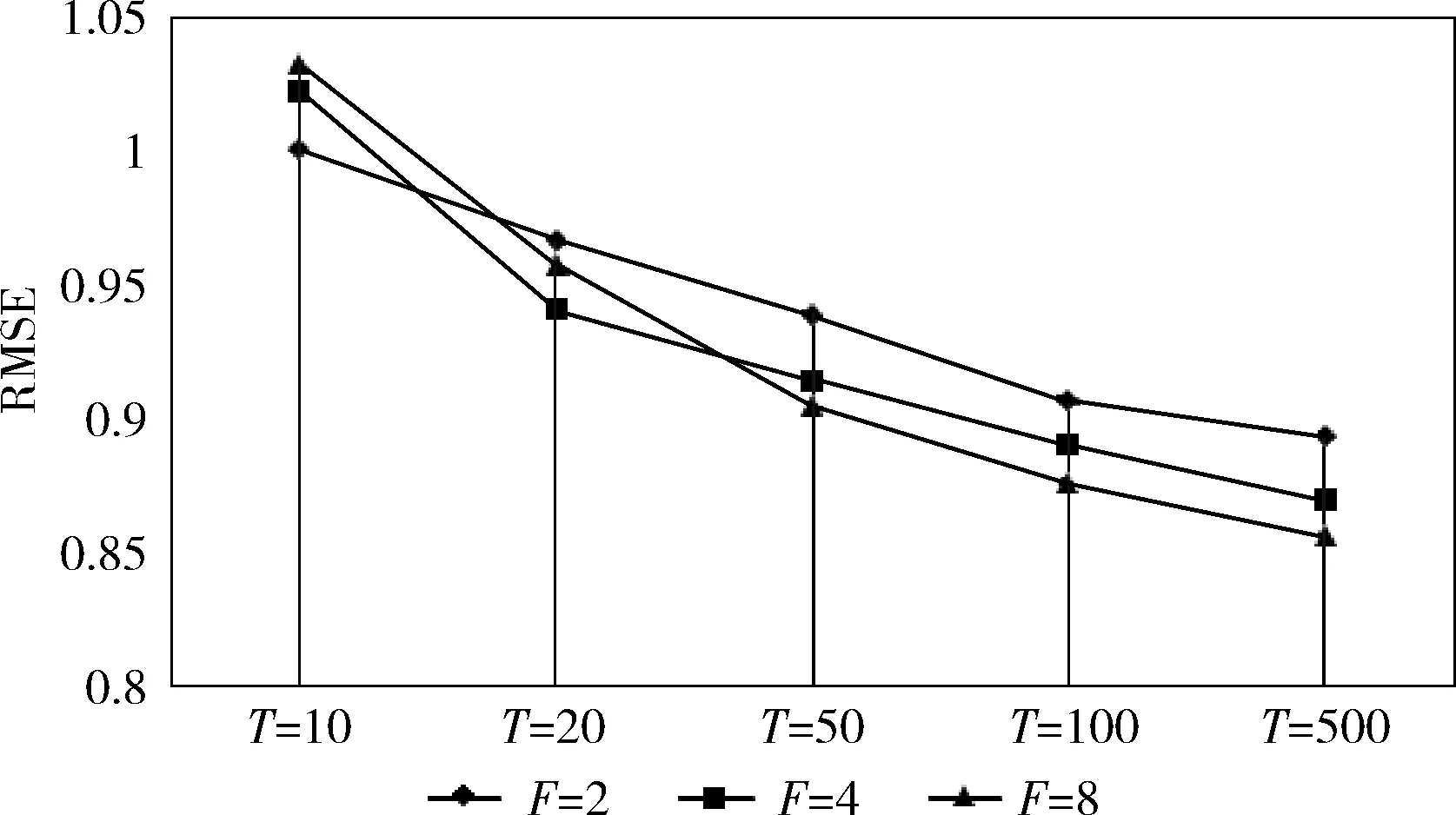
图4 不同特征数量下L-BFGS-CF的RMSE值对比

图5 不同特征数量下L-BFGS-CF的MAE值对比
3.2.3 L-BFGS-CF算法收敛速度分析
选取特征数量为4个的情况下使用不同迭代次数T考查算法收敛速度,结果如图6和图7所示。L-BFGS-CF算法的RMSE和MAE值随着迭代次数的增加而逐渐变小,表明迭代次数是计算精度的主要影响因素之一。而不同大小的数据集来看,随着数据集的增大,算法的RMSE和MAE值逐步减小;此外算法在迭代次数为10-50次的精度提升最为明显。对于TMALL-10M数据,由于布尔类型的预测结果,在迭代次数50次左右达到相对稳定点。

图6 不同迭代次数L-BFGS-CF的RMSE值对比
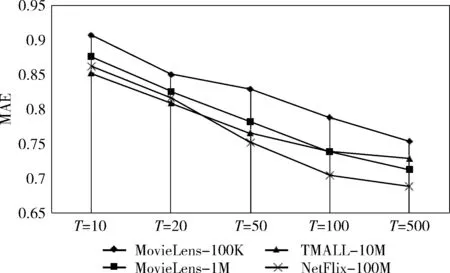
图7 不同迭代次数L-BFGS-CF的MAE值对比
综上可知,与其它3种协同过滤算法相比,L-BFGS-CF算法在规模不同的数据集均有最小的RMSE和MAE值,算法在迭代次数为50次可达到较好的精度,收敛速度快,且在适当增加迭代次数和数据集特征数量时能得到更好的预测精度。
4 结束语
本文针对所提出的基于L-BFGS优化的协同过滤算法的研究结论如下:
(1)算法设计上,采用FM模型对评分进行预测,FM模型使用辅助向量对的特征组合系数进行估计,避免了训练数据的稀疏性对参数学习的影响;采用L-BFGS算法训练模型具有收敛速度快和占用计算空间低等特点,在数据量剧增的云环境下具有良好的可扩展性。
(2)实验结果表明:与SVD++、KNN-100和基于聚类的协同过滤算法相比,本算法的RMSE值分别降低了0.198,0.085,0.056;MAE值分别降低了0.142,0.063,0.04。在4种规模的数据集上都取得了最小的RMSE和MAE值,具有良好的推荐精度。同时在适当增加迭代次数和数据集特征可以取得更好的推荐质量。本文在Spark分布式计算框架实现本算法,有效提高了算法计算效率和保证推荐系统的实时性,更适合云环境下的个性化推荐问题。
未来的研究工作考虑将Fuzzy C-means聚类算法与本算法结合,在进一步节省计算资源消耗的同时提高算法推荐精度。
[1]Yang X,Guo Y,Liu Y,et al.A survey of collaborative filtering based social recommender systems[J].Computer Communications,2014,41(5):1-10.
[2]Hernando A,Bobadilla J,Ortega F.A non negative matrix factorization for collaborative filtering recommender systems based on a Bayesian probabilistic model[J].Knowledge-Based Systems,2016,97(C):188-202.
[3]WEI Suyun,XIAO Jingjing,YE Ning.Collaborative filtering algorithm based on Co-clustering smoothing[J].Journal of Computer Research and Development,2013,50(s2):163-169(in Chinese).[韦素云,肖静静,业宁.基于联合聚类平滑的协同过滤算法[J].计算机研究与发展,2013,50(s2):163-169.]
[4]Cobos C,Rodriguez O,Rivera J,et al.A hybrid system of pedagogical pattern recommendations based on singular value decomposition and variable data attributes[J].Information Processing & Management,2013,49(3):607-625.
[5]Zhou X,He J,Huang G,et al.SVD-based incremental approaches for recommender systems[J].Journal of Computer and System Sciences,2015,81(4):717-733.
[6]NIU Changyong,LIU Guoshu.Collaborative filtering algorithm based on both local and global similarity and singular value decomposition(SVD)[J].Computer Engineering and Design,2016,37(9):2497-2501(in Chinese).[牛常勇,刘国枢.基于局部全局相似度的SVD的协同过滤算法[J].计算机工程与设计,2016,37(9):2497-2501.]
[7]Tsai CF,Hung C.Cluster ensembles in collaborative filtering recommendation[J].Applied Soft Computing,2012,12(4):1417-1425.
[8]CHEN Kehan,HAN Panpan,WU Jian.User clustering based social network recommendation[J].Chinese Journal of Computers,2013,36(2):349-359(in Chinese).[陈克寒,韩盼盼,吴健.基于用户聚类的异构社交网络推荐算法[J].计算机学报,2013,36(2):349-359.]
[9]DENG Xiaoyi,JIN Chun,HAN Qingping,et al.Improved collaborative filtering model based on context clustering and user ranking[J].Systems Engineering-Theory & Practice,2013,33(11):2945-2953(in Chinese).[邓晓懿,金淳,韩庆平,等.基于情境聚类和用户评级的协同过滤推荐模型[J].系统工程理论与实践,2013,33(11):2945-2953.]
[10]Rendle S.Factorization machines with libfm[J].ACM Transactions on Intelligent Systems and Technology,2012,3(3):57.
[11]Baltrunas L,Ricci F.Experimental evaluation of context-depen-dent collaborative filtering using item splitting[J].User Modeling and User-Adapted Interaction,2014,24(1-2):7-34.
[12]Salah A,Rogovschi N,Nadif M.A dynamic collaborative filtering system via a weighted clustering approach[J].Neurocomputing,2016,175(A):206-215.
[13]Nilashi M,Jannach D,Bin Ibrahim O,et al.Clustering-and regression-based multi-criteria collaborative filtering with incremental updates[J].Information Sciences,2015,293(1):235-250.
[14]ZHANG Bangzuo,GUI Xin,HE Tang,et al.A novel reco-mmender algorithm on fusion heterogeneous information network and rating matrix[J].Journal of Computer Research and Development,2014,51(s2):69-75(in Chinese).[张邦佐,桂欣,何涛,等.一种融合异构信息网络和评分矩阵的推荐新算法[J].计算机研究与发展,2014,51(s2):69-75.]
[15]Biglari F.Dynamic scaling on the limited memory BFGS met-hod[J].European Journal of Operational Research,2015,243(3):697-702.
[16]LI Weitao,ZHOU Yuanfeng,GAO Shanshan,et al.Rapid sampling on implicit surfaces via hybrid optimization[J].Chinese Journal of Computers,2014,37(3):593-601(in Chinese).[李伟涛,周元峰,高珊珊,等.基于混合优化的快速隐式曲面采样方法[J].计算机学报,2014,37(3):593-601.]
[17]Biglari F,Ebadian A.Limited memory BFGS method based on a high-order tensor model[J].Computational Optimization and Applications,2015,60(2):413-422.
[18]Liu H,Hu Z,Mian A,et al.A new user similarity model to improve the accuracy of collaborative filtering[J].Know-ledge-Based Systems,2014,56(3):156-166.

