GLUE框架下似然函数对水文模型不确定性的影响
姜倩妮, 李占玲, 张永勇
(1.中国地质大学(北京) 水资源与环境学院, 北京 100083; 2.中国科学院地理科学与资源研究所 陆地水循环及地表过程重点实验室, 北京 100101)
1 研究背景
水文模型是探索自然界水循环过程的重要手段,如今已经广泛应用在水资源管理、水文预报等方面。随着对水文循环过程的不断了解和计算机性能的不断提高,水文过程的模拟已经越来越精确。但由于更为复杂水文过程的引入,模型对水文物理过程描述的逐渐增加、模型结构呈现复杂化趋势[1],由此也导致模型参数的不断增加。谨慎地率定参数和分析参数的不确定性,对于提高水文预报精度具有重要意义。
普适似然不确定性估计法(GLUE:Generalized Likelihood Uncertainty Estimation)目前已广泛应用在参数的率定和不确定性分析中[2-4],该方法是Beven和Binley在1992年基于“异参同效”现象提出的[5]。与其它不确定性分析方法相比,GLUE方法操作简单并可通过灵活定义似然函数来分离可行和不可行参数组[6]。似然函数是GLUE方法的重要组成部分,对参数的率定和不确定性分析产生一定的影响。目前单目标GLUE方法中,Nash-Sutcliffe系数(NSCE)是最常用的似然函数[7-8],但NSCE仅能描述一部分的水文过程,如刘艳丽等[9]将NSCE单个似然判据扩展为洪峰误差、洪量、峰现时间、NSCE4个目标的多准则似然判据时,能更好地反映模型的实际不确定性情况。考虑多个似然函数的GLUE方法虽然综合描述了多个水文过程,但权重的主观分配进一步增加了参数的不确定性[10-11]。
目前基于单目标的GLUE方法评价参数不确定性的研究已经有很多,但不同似然函数对参数敏感性和不确定性的影响评价研究还比较少。本文以淮河上游大坡岭控制流域为例,探索了GLUE框架下NSCE和水量平衡系数作为似然函数对流域水循环模型参数敏感性和不确定性的影响,旨在为GLUE方法中似然函数的选取以及为多目标GLUE方法权重的分配提供参考依据。
2 水循环模型与GLUE方法
2.1 流域水循环模型
模型采用ZhangYongyong等[12]于2012-2015年期间自主开发的流域水循环系统模型(Hydrological,EcologicalandwaterQualityModel:HEQM)。该模型以水和营养物(碳、氮和磷)循环作为联系流域内与水相关各过程的纽带,综合考虑水文过程和营养物循环在陆面、土壤、植被和河流水体中的相互作用关系及闸坝调控、排污等人类活动对水和营养物循环的影响[12]。HEQM包含八大模块,本文主要采用水文循环模块。其关键的水量平衡方程为:
Pi+SWi=SWi+1+Rsi+Eai+Rssi+Rbsi+Ini
(1)式中:P为降水,mm;SW为土壤湿度,mm;Ea为实际蒸散发,mm,包括土壤蒸发(Es, mm)和植被蒸散发(Ep,mm);Rs、Rss和Rbs分别为地表径流、壤中流和基流,mm;In为植被截留,mm;i为时间步长,d。
方程(1)中地表径流Rs的计算采用时变增益产流方程(Time Variant Gain Model: TVGM)[13];壤中流Rss和基流Rbs分别与上下层土壤湿度呈线性关系;潜在蒸散发的计算采用Hargreaves方法[14];实际蒸散发包括植被蒸腾和土壤蒸发,植被蒸腾通过潜在蒸散发量和叶面积指数获得,土壤蒸发通过潜在蒸发量和表层土壤残余度获得;上下层水流之间的运动采用土壤蓄水演算法;河道汇流演算采用马斯京根法或动力波方程。
2.2 GLUE方法
作为分析参数不确定性的重要方法,GLUE方法的重要观点是,模型模拟结果的好坏不是由模型中的某个参数所决定,而是由一组模型参数来决定。一般的参数率定只选出一组最优的参数组作为模型的参数,但是因为“异参同效”现象,“最优参数”很难获得,GLUE方法通过选取似然函数,设置阈值,筛选“可行参数组”,分析模拟结果的不确定性[5],可以避免“异参同效”现象带来的影响。
GLUE方法参数敏感性和模拟结果的不确定性分析步骤如下:
(1)选择似然函数。似然函数是评价水文过程模拟好坏的重要指标。本文选取NSCE和水量平衡系数作为似然函数,分别从时间和水量两个方面描述水文过程,其计算公式如下:
Nash-Sutcliffe系数:
(2)
水量平衡系数:
(3)
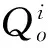
(2)模型参数范围的确定和先验分布的选取。对于模型参数的选取和取值范围的确定,参考相关文献[12]并根据模型参数的物理特征,确定参数的初始范围。由于先验信息不足,无法准确描述先验分布,通常选择均匀分布作为先验分布。
(3)参数抽样及其优化。参数优化采用SCE-UA单目标自动优化算法。SCE-UA优化算法可以解决复杂水文模型参数的优选问题,由DuanQingyun等[15]结合单纯性法、随机搜索和生物竞争进化方法的优点而研发的。
(4)确定阈值。阈值的选取带有一定的主观性,本文将NSCE的阈值设定为0.7;水量平衡系数在-0.05~0.05之间。如果似然值满足阈值条件,其对应的参数集称为可行参数集,反之则为不可行参数集。
(5)参数的不确定性分析。根据参数组模拟情况确定可行参数组,绘制模型参数与似然值的散点图、可行参数组频率直方图,定性分析模型参数的不确定性。在散点图中,若参数似然分布接近于原始均匀分布,则参数对目标函数的影响不显著,为不敏感性参数;反之,则为敏感性参数。在频率直方图中,各参数分布的形状表明估计的不确定性的频率,参数在某一值处的频率越低说明参数具有越多的不确定性。
(6)模拟结果不确定性评估。给每个可行参数组一个权重,模型输出不确定性用权重化后的参数组决定的输出分位数表示,即基于95%置信区间对应的分位数组成的预测区间。同时还要对模拟结果的不确定性进行评估。
对于不确定性结果的区间估计,本文选取比较常用的2个指标,即覆盖率CS和平均对称度S[16]。CS表示预测区间包含实测流量的比例,通常用百分比表示,CS越接近100%则说明模拟值接近实测值的可能性越大,模拟效果越好。在绝对对称的情形及理想情况下,S值为0;若S<0.5,则说明在平均水平上流量过程线在预测不确定性区间内;若S≥0.5,则说明平均水平上流量过程线在预测不确定性区间之外,而且S越大则不确定性区间的性能越差。其公式如下:
(4)
式中:nQin为实测值落在置信区间的个数;n为可行参数的个数。

3 实例分析
3.1 研究区概况与水循环模型构建
本文研究区为淮河上游的大坡岭流域(E113°15′~114°46′,N31°31′~32°43′),流域面积为1 573.3km2,见图1。流域内分布有回龙寺、黄岗、毛集、潘庄、固县等13个雨量站,多年平均降雨量为918mm,其中50%集中在汛期( 6-9月),而多年平均气温11~16℃。流域地形呈现山脉较多,坡度较大的特点。流域出口大坡岭水文站历年最高水位为104. 86m,最大洪峰流量为4 200m3/s[17]。
研究搜集了数字高程模型(DEM: 90m×90m)、 土地利用(1km×1km)等GIS数据,包括流域内13个雨量站点1994-2002年日降水序列、以及大坡岭水文站日径流序列。利用ArcGIS平台提取HEQM所需的流域属性数据;并利用泰森多边形方法求得该流域的面雨量序列,驱动已构建的模型,进而模拟大坡岭断面日径流过程。选取1994年为模型预热期,1995-1999年为模型率定期,2000-2002年为模型验证期。HEQM模型水文相关的参数主要有9个,其中与土壤有关的参数5个:土壤稳定下渗率(fc)、上层饱和土壤含水量(WM)、土壤水出流系数(Kr) 、田间持水量(WMc),土壤蒸散发补充系数(ketp);与地表水有关的参数2个:产流参数g1和g2;地下水有关参数2个:地下水出流系数(Krg),水滞留时间(Tg)[12]。具体的参数范围见表1。

图1 大坡岭流域图

类别参数初始取值范围NSCE阈值为0.7参数取值范围水量平衡系数满足条件的为在±0.05之间土壤稳定下渗率(fc)/(mm·h-1)0~120.0038.00~120.000~120.00饱和土壤含水量(WM)0.45~0.750.45~0.500.45~0.70土壤土壤水出流系数(Kr)0~1.000.36~0.720~1.00土壤田间持水量(WMc)0.20~0.450.26~0.360.20~0.45土壤蒸散发补充系数(ketp)0~2.000.50~0.810~1.90地表水g1调整系数0~3.001.60~3.000~3.00g2调整系数0~3.001.20~2.100~3.00地下水地下水出流系数(Krg)0~1.000.54~1.000~1.00地下水滞留时间(Tg)/d1.00~100.001.00~3.201.00~97.00
3.2 以效率系数为似然函数的参数不确定性分析
3.2.1 参数敏感性分析 利用SCE-UA算法,随机均匀抽取的10 000组参数分别运行HEQM模型,模拟大坡岭流域日径流量的过程,最终获得NSCE大于0.7的参数似然函数散点图、可行参数频率直方图,见图2,可行参数组的取值范围见表1。筛选的9个参数形成的散点图均有明显的峰值,可作为模型的敏感性参数。其中可行参数的取值范围与初始范围变化最为明显的是与土壤有关的参数fc、ketp和与地下水有关的参数Tg,分别由原来的0~120.00mm/h、0~2.00和1~100.00d,缩小到38.00~120.00mm/h、0.50~0.81和1~3.20d。因此,以NSCE为似然函数的GLUE方法可有效缩小部分参数的取值范围;另外,这9个参数均具有良好的单峰分布,其中fc的取值主要集中在80~100mm/h,ketp的取值在0.50~0.75,其他7个参数的取值均在一定范围内比较稳定。通过对各组可行参数的频率分析得:以NSCE为似然函数选取的可行参数值出现较高频次的范围比较集中,这进一步减小了参数的不确定性。由于篇幅有限,本文只展示土壤稳定下渗率和蒸散发补充系数相关结果,见图2。
3.2.2 模拟结果的不确定性分析 根据筛选的可行参数组模拟每组参数对应的径流过程,计算获得95%置信度下NSCE作为似然函数时大坡岭日径流模拟的不确定性区间,见图3。结合不确定性评价指标,可以看出:在率定期和验证期模拟的日径流序列区间涵盖了26.2%和15.8%的实测值;当观测值很大或者很小时,均不能将其涵盖,特别是在验证期。这可能是由于模型结构的不确定性或者人为选取阈值的原因。
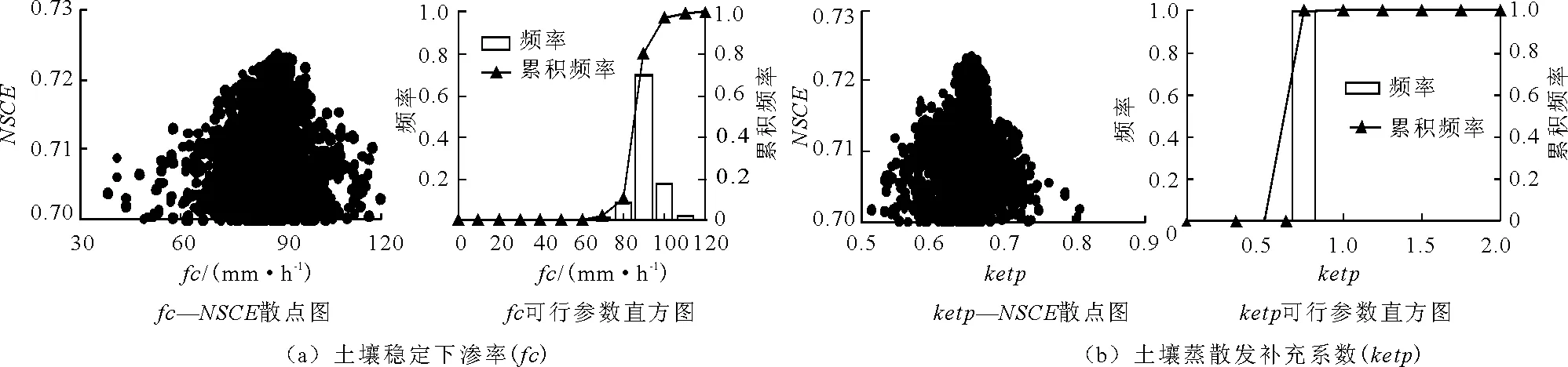
图2 参数-NSCE散点图与可行参数组频率直方图

图3 95%置信度下NSCE系数作为似然函数的率定期和验证期的不确定性范围
3.3 以水量平衡系数为似然函数的参数不确定性分析
3.3.1 参数的敏感性分析 参数-水量平衡系数散点图与可行参数组频直方图见图4。从水量平衡系数在±0.05之间的可行参数组的取值范围可以看出,绝大部分满足似然判据的参数取值范围与原始取值范围相同,只有ketp和Tg从原始的0~2.00、1~100.00d缩小至0~1.90和1~97.00d。从图4(a)可以看出,仅fc为敏感性参数;而从图4(b)可以看出,fc取值范围在80.00~100.00 mm/h之间时,ketp的取值主要集中在0.50~0.75,其余7个参数的取值范围均在一定的范围内,在此范围内,参数的不确定性较小,在此范围外参数的不确定性增加;以水量平衡系数作为似然函数时,只有fc为敏感性参数,增加了模型的不确性。由于篇幅有限,本文也只展示土壤稳定下渗率和蒸散发补充系数相关结果(图4)。
3.3.2 模拟结果的不确定性分析 从不确定性区间来看(图5):在率定期和验证期模拟的径流序列区间涵盖了44.5%和32.1%的实测值;并不能涵盖峰值较大的实测径流量,特别是在验证期。这可能是由于模型结构的不确定性或者人为选取阈值的原因。
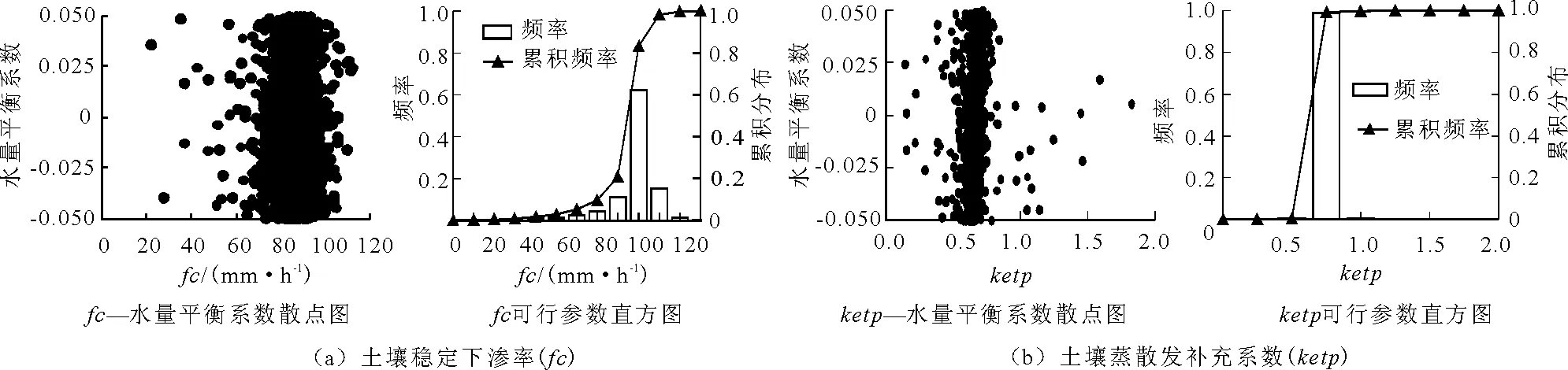
图4 参数-水量平衡系数散点图与可行参数组频率直方图

图5 95%置信度下水量平衡系数作为似然函数的率定期和验证期不确定区间
3.4 不同似然函数的结果比较
通过比较NSCE和水量平衡系数两个似然函数对模型参数敏感性的影响,可以看出:似然函数选取对模型参数的敏感性分析影响很大。以NSCE作为似然函数时,9个与水文有关的参数均较敏感,且参数的最终取值范围缩小;但以水量平衡系数作为似然函数时,只有fc是敏感性参数。说明参数的敏感性与似然函数的选取有很大关系,以“时间”属性的NSCE和“水量”属性的水量平衡系数由于考虑了不同水文过程,衡量的标准也不同。但是从参数集中出现的范围来看,这两种似然函数参数主要集中的范围相似。值得注意的是,虽然fc在两种似然函数判别下均为敏感性参数,但是其散点图形状却有很大不同,在NSCE作为似然函数时,fc有非常明显的波峰和波谷,但是在水量平衡系数作为似然函数时,其数值范围明显缩小,呈现类似于“柱状”的图形。
通过图3和5可以看出,无论是在率定期还是验证期,水量平衡系数作为似然函数的模拟结果要好于NSCE作为似然函数时的模拟结果,特别是在率定期流量较大的时候。这可能与水量平衡系数作为似然函数时,各参数取得的可行参数集取值范围较大有关,参数集能够充分体现模型模拟的不确定性区间。
根据实测值在置信区间内数量评价模拟结果的不确定性(表2)。可以看出以NSCE作为似然函数时,验证期和率定期的覆盖率较低,分别为26.2%和15.1%;以水量平衡系数作为似然函数时,验证期和率定期的覆盖率分别为44.5%和32.1%,说明水量平衡系数作为似然函数,对不确定区间评价的结果要优于NSCE;此外,从平均对称度S看,NSCE作为似然函数时,验证期和率定期的对称度分别为0.26和0.25;以水量平衡系数作为似然函数时,验证期和率定期的对称度分别为0.23和0.25,也可证明水量平衡系数作为似然函数,选取的不确定性区间要优于NSCE作为似然函数选取的不确定性区间。

表2 两种似然函数的不确定性区间评价结果
4 结 论
本文以淮河流域上游大坡岭控制流域为研究区,分析了GLUE框架下不同似然函数对模型参数选取和模拟结果的影响,主要的结论如下:
(1)在不同的似然函数条件下,HEQM模型参数的取值范围明显不同。以NSCE作为似然函数时,9个参数的取值范围缩小较大,其中fc、ketp和Tg3个参数的取值范围缩小最大;以水量平衡系数作为似然函数时,参数范围没有明显变化;在不同的似然函数条件下,参数对模型的敏感性也不同,以NSCE作为似然函数时,9个参数的散点图均有明显的波动,因此9个参数均为敏感性参数;而以水量平衡系数作为似然函数时,只有fc是敏感性参数。
(2)NSCE和水量平衡系数均可作为GLUE方法的似然函数,但从参数不确定性区间评价结果来看,水量平衡系数作为似然函数时,覆盖率和对称度均好于NSCE作为似然函数。特别是对于极端径流,水量平衡系数作为似然函数的GLUE方法对参数的不确定性分析更为准确。
参数的敏感性和不确定性与似然函数的选取密切相关,在今后的研究中可以选取更多具有代表性的似然函数,来分析似然函数与参数之间的关系,从而为多目标似然函数的权重分配提供理论依据。
[1]SHENZhenyao,CHENLei,CHENTao.AnalysisofparameteruncertaintyinhydrologicalandsedimentmodelingusingGLUEmethod:acasestudyofSWATmodelappliedtoThreeGorgesReservoirRegionChina[J].HydrologyandEarthSystemSciences,2012,16(1):121-132.
[2] 张质明,王晓燕,于 洋,等.基于GLUE法的多指标水质模型参数率定方法[J].环境科学学报,2014,34(7):1853-1861.
[3] 舒 畅,刘苏峡,莫兴国,等.新安江模型参数的不确定性分析[J].地理研究,2008,27(2):343-352.
[4]MCCONNELLP.Hydrologicalforecastinguncertaintyassessment:IncoherenceoftheGLUEmethodology[J].JournalofHydrology,2006,330(1-2):368-381.
[5]KEITHB,BINLEYA.Thefutureofdistributedmodels:modelcalibrationanduncertaintyprediction[J].HydrologicalProcesses,1992,6(3):279-298.
[6]BLASONERS,MADSENH,DANR.UncertaintyassessmentofintegrateddistributedhydrologicalmodelsusingGLUEwithMarkovchainMonteCarlosampling[J].JournalofHydrology,2008,353(1-2):18-32.[7]SELLAMIH,BENABDALLAHS,JEUNIESSEIL,etal.ClimatemodelsandhydrologicalparameteruncertaintiesinclimatechangeimpactsonmonthlyrunoffanddailyflowdurationcurveofaMediterraneancatchment[J].InternationalAssociationofScientificHydrologyBulletin,2016,61(8):1415-1429.[8]ARABIM,RAOSG,HANTUSHMM.Aprobabilisticapproachforanalysisofuncertaintyintheevaluationofwatershedmanagementpractices[J].JournalofHydrology,2007,333(2-4):459-471.
[9] 刘艳丽,梁国华,周惠成.水文模型不确定性分析的多准则似然判据GLUE方法[J].四川大学学报(工程科学版),2009,41(4):89-96.
[10]SUNMei,ZHANGXiaoling,HUOZailing,etal.Uncertaintyandsensitivityassessmentsofanagricultural-hydrologicalmodel(RZWQM2)usingtheGLUEmethod[J].JournalofHydrology,2016,534:19-30.
[11] 王纲胜,夏 军,陈军锋.模型多参数灵敏度与不确定性分析[J].地理研究.2010,29(2):263-270.[12]ZHANGYongyong,SHAOQuanxi,YEAizhong,etal.Integratedwatersystemsimulationbyconsideringhydrologicalandbiogeochemicalprocesses:modeldevelopment,withparametersensitivityandautocalibration[J].HydrologyandEarthSystemSciencesDiscussions,2016,12(5):4997-5053.[13]XIAJun.IdentificationofaconstrainednonlinearhydrologicalsystemdescribedbyVolterraFunctionalSeries[J].WaterResourcesResearch,1991,27(9):2415-2420.[14]HARGREAVESGH,SAMANIZA.Estimatingpotentialevapotranspiration[J].JournaloftheIrrigationandDrainageDivision,1982,108(3):225-230.[15]DUANQingyun,SOROOSHS,VIJAIG.Effectiveandefficientglobaloptimizationforconceptualrainfall‐runoffmodels[J].WaterResourcesResearch,1992,28(4):1015-1031.[16]XIONGLihua,WANMin,WEIXiaojing,etal.Indicesforassessingthepredictionboundsofhydrologicalmodelsandapplicationbygeneralizedlikelihooduncertaintyestimation[J].InternationalAssociationofScientificHydrologyBulletin,2009,54(5):852-871.
[17] 周敏敏,瞿思敏,石 朋,等.淮河上游大坡岭流域土地利用方式变化引起的流域滞时变化[J].河海大学学报(自然科学版),2015,43(2):100-106.

