基于GRA-MEA-BP耦合模型的城市需水预测研究

李晓英，苏志伟，田佳乐，郑景耀

(河海大学 水利水电学院， 江苏 南京 210098)

1 研究背景

城市需水预测是城市水资源管理与规划中的重要环节，同时也是供水系统优化调度的基础内容之一。现有的需水预测方法主要有：粒子群法、灰色模型、人工神经网络、回归模型、随机森林模型[1-7]等。人工神经网络具有自适应、自学习、自组织等智能功能，在预测领域得到广泛应用，其中BP神经网络结构简单、易于实现。何斌等[8]基于 BP神经网络对辽西大凌河进行泥沙预测，计算精度良好，可为下游泥沙量提供预报；崔吉峰等[9]采用基于粒子群改进BP神经网络的组合预测模型对我们能源需求进行分析研究；臧东伟等[10]采用遗传算法优化神经网络的模型，对南京市进行了需水预测分析，经验证模型能较好的预测城市需水量；舒媛媛等[11]采用基于主成分分析的BP神经网络对延安市进行了需水分析；杨婷等[12]建立了GM(1，1)模型和BP神经网络相耦合的灰色BP模型，对民勤盆地地下水动态水埋深进行了预测分析。

思维进化算法作为一种新型进化算法，延续了遗传算法的部分理念，与遗传算法不同的是增加了趋同、异化两种操作，在计算效率和收敛性方面优于遗传算法，思维进化算法在多个领域得到应用。张以帅等[13]采用基于思维进化算法优化BP神经网络，对银川某县进行了短期天然气预测分析；赵瑞勇等[14]建立了基于MEA优化BP神经网络预测模型，对微波加热褐煤温度进行了预测；杜晓[15]基于MEA-BP模型进行了股票预测分析；吴伟等[16]在医学领域应用了思维进化算法，建立了MEA-BP预测模型对肾综合征出血热发病率进行了预测研究。

基于上述研究，本文以泰州市需水量预测为研究对象，提出GRA-MEA-BP耦合预测模型，通过灰色关联分析筛选需水量主要影响因子，采用MEA优化BP神经网络权值与阈值以达到网络结构简化、预测精度提高等目的，为城市需水预测提供一种新的有效研究方法。

2 基本原理及方法

2.1 灰色关联分析

灰色关联分析(Grey relational analysis，GRA)是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度[17]。灰色关联分析通过对动态过程发展态势的量化分析，完成对系统内时间序列有关统计数据几何关系的比较，求出参考数列与各比较数列之间的灰色关联度。本文灰色关联分析具体步骤如下：

第1步：确定以城市年需水量为特征的参考数列和降水量、GDP、人口等影响因子的比较数列；

第2步：无量纲化处理参考数列及比较数列；

第3步：计算参考数列与比较数列的灰色关联系数ξi(k)；

(1)

式中： ρ为分辨系数，其作用在于提高系数间的差异显著性，一般取为0.5。

第4步：计算年需水量作为参考数列与比较数列的关联度r；

(2)

式中： ri为序列Xi与序列X0的关联度。

2.2 BP神经网络

BP神经网络是一种以误差逆向转递的多层前反馈网络。其学习规则采用梯度下降算法，输入向量首先正向传递到隐含层，经过传递函数计算，将结果传递到输出层，即得到输出结果。若实际输出结果与期望输出结果存在误差时，则进行误差反向传递，根据预测误差来调整网络权值与阈值，从而使BP神经网络预测输出不断逼近期望误差，最终达到设定期望误差或设定学习次数作为网络学习终止条件。主要步骤如下：

步骤1：将需水量影响因子作为网络模型输入参数，将年需水量作为输出参数；

步骤2：将输入参数进行归一化处理；

步骤3：选取泰州市2002-2010年数据为训练样本，2011-2014年数据为检验样本对网络模型进行训练，在精度满足后，输出预测数据；

步骤4：将模型计算得到数据与实际值进行对比分析。

2.3 思维进化算法(MEA)

思维进化算法属于进化算法的一种，其系统结构图如图1所示。

图1 思维进化算法系统结构

思维进化算法学习步骤如下：

步骤1：初始种群个体在解空间随机散步，计算每个个体得分，搜索得分最高的若干临时个体和优胜个体；

步骤2：以优胜个体和临时个体分别为中心，在个体周围产生新的个体，从而得到若干优胜子种群和临时子种群；

步骤3：子种群内部进行趋同操作，直到子种群成熟，以该子种群最优个体得分为该子种群得分；

步骤4：将各子种群得分粘贴在全局公告板上，子种群之间进行异化操作，完成临时种群的替代、废弃等过程，从而计算全局最优个体及其得分。

2.4 GRA-MEA-BP耦合模型

首先利用灰色关联分析筛选出需水量主要影响因子，后采用思维进化算法来优化BP神经网络的初始值与阈值，使优化后的BP神经网络能够更好地预测函数输出，最后利用训练好的网络进行需水预测，其流程图如图2所示。

图2 GRA-MEA-BP模型流程图

3 实例应用

3.1 研究区域概况

泰州位于江苏省中部，长江北岸，北部与盐城毗邻，东邻南通，西接扬州，是苏中入江达海5条航道的交汇处。全境属于亚热带季风气候，四季分明，雨量夏丰冬少，实现合理利用水资源，对社会经济及城市的发展具有重要的意义。因此，有必要对泰州市进行需水量预测，为城市合理分配水资源提供依据。

3.2 基于灰色关联分析的模型输入参数选定

在充分考虑需水量影响因子的基础上，依据泰州市水资源公报，以2002-2014年为时间序列，初步选择10个因子作为泰州市需水量影响因子，其中X1为降水量、X2为GDP、X3为人口、X4为农业用水量、X5为工业用水量、X6为生活用水量、X7为第一产业产值、X8为第二产业产值、X9为第三产业产值、X10为耕地面积，对以上数据进行标准化处理后进行经灰色关联度计算，一般关联阈值在[0.7,0.8]区间内关联度处于较高状态，本文关联阈值取为0.75，即选择关联值大于0.75的因子作为主影响因子，结果按大小排序如下表1所示。最终选用生活用水量、耕地面积、降水量、第一工业产值、农业用水量、第三工业产值、人口7个因子作为网络的输入量。

表1 各影响因子与需水量之间的关联排序

3.3 GRA-MEA-BP耦合模型构建

将选取的7个因子作为模型的输入量，泰州市总用水量作为输出量，建立3层的GRA-MEA-BP耦合模型，经试算：隐含层个数选定为12，即网络拓扑结构最终选为7-12-1。从样本中选取2002-2010年数据作为训练样本，2011-2014年数据作为检验样本。由于样本数据的量纲及数量级不相同，首先对样本数据进行归一化处理，再输入到模型中进行学习训练。其中，MEA网络参数设定如下：种群规模100，优胜子种群5，临时子种群5，迭代次数10，通过学习训练后得到预测模型。同时建立BP神经网络作为对比模型，网络拓扑结构同样选为7-12-1。

3.4 需水预测结果与分析

选用相对误差e和均方差σ作为需水预测模型评价的标准，其计算公式如下：

(3)

(4)

经过第一次迭代，优胜子种群和临时子种群趋同过程如图3、4所示，在经过第二次迭代后各优胜子种群得分已不再变化，如图5、6所示，将二次迭代后的子种群进行异化操作，得到最优权值阈值，将得到的权值阈值输入到BP网络进行训练学习，得到各年份的预测需水量。同时用BP网络进行预测分析，结果如表2所示。

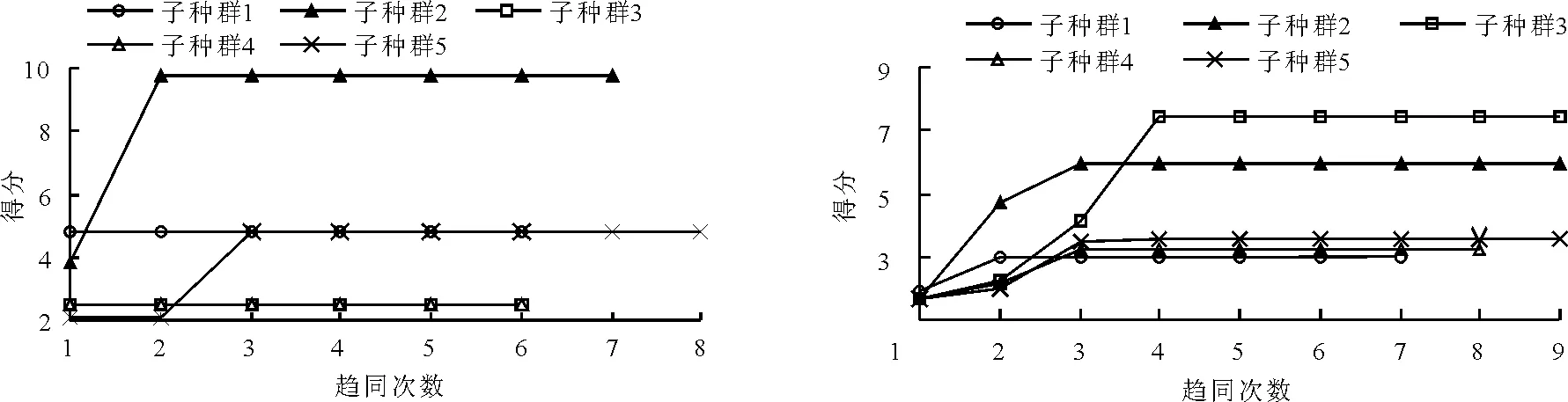
图3 初始优胜子种群趋同过程 图4 初始临时子种群趋同过程

图5 第二次迭代优胜子种群趋同过程 图6 第二次迭代临时子种群趋同过程

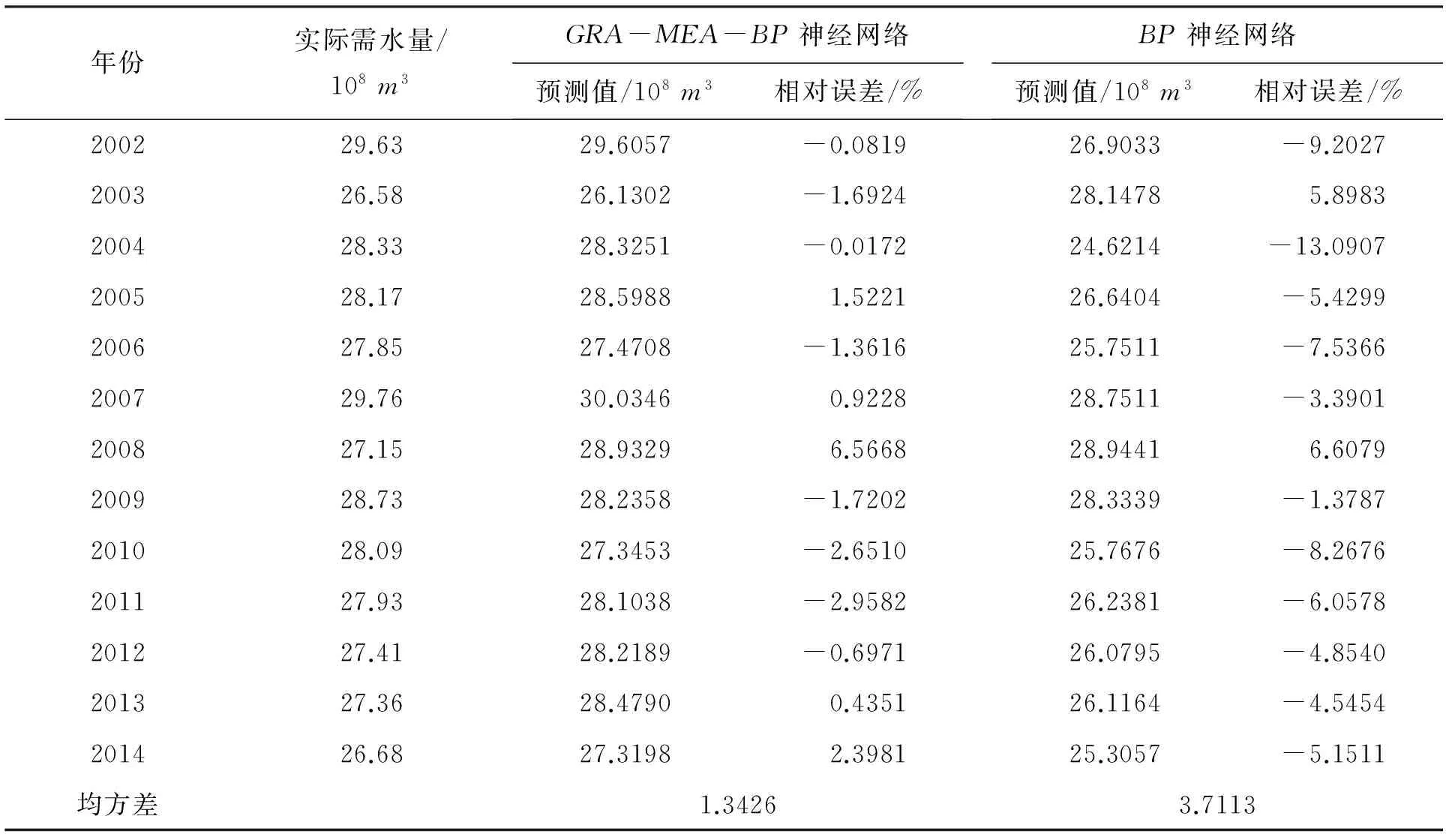
表2 GRA-MEA-BP预测模型与BP预测模型的拟合结果比较

由表2数据，对2002-2014年泰州市需水量预测中GRA-MEA-BP耦合模型最大相对误差绝对值为6.5668%，均方差为1.3426;BP神经网络预测模型最大相对误差绝对值为13.0907%，均方差为3.7113，可见GRA-MEA-BP耦合模型预测精确度优于BP神经网络模型，在实际程序运行中GRA-MEA-BP耦合模型经2次迭代就达到收敛，而BP神经网络则经过312步才达到收敛，可知GRA-MEA-BP耦合模型运行速度也优于BP神经网络模型。

由训练样本(2002-2010年)预测数据可见，GRA-MEA-BP耦合模型最大相对误差绝对值为6.5668%，BP神经网络模型最大相对误差绝对值达到了13.0907%，耦合模型在训练阶段就优于BP神经网络模型，达到了较高的精确度。

对于检验样本(2011-2014年)预测数据，从表2数据结果可知，BP神经网络模型对于2011-2014年的检验样本拟合均偏小，总体变化趋势与实际需水量变化趋势差异较大，而GRA-MEA-BP网络模型则在2011-2014年的检验样本中预测值与实际值更为符合，总体预测趋势也符合实际情况，可见GRA-MEA-BP耦合模型与原始序列吻合程度优于BP神经网络模型，可作为需水预测的一种有效、可行的方法。

4 结 论

(1)以泰州市为例，通过灰色关联分析，从10个需水量影响因子中筛选出了7个影响因子，作为预测模型的输入量，有效的降低了网络的复杂性，同时也进一步的提高预测速度与精确度。

(2)由于思维进化算法具有全局搜索的能力，将其用于优化神经网络的权值和阈值，通过实例验证表明，其有效的改善了神经网络的预测速度和预测精度，GRA-MEA-BP耦合预测模型与原始序列吻合度良好。

(3)本文用灰色关联分析法确定了需水预测的主要影响因子，但是这些因子都是选自于历年可量化的数据，并未考虑到系统内部因素，如节水因素、突发事件等因素对需水预测的影响，因此，需水预测模型还不够完备，有待进一步优化。

[1] 郭 华,郑 侃,林占东,等. 粒子群算法在城市需水预测模型中的应用[J]. 中国农村水利水电, 2008(12): 63-65.

[2] 张琼楠,张 龙. 改进的灰色GM(1,1)模型在农业需水预测中的应用[J]. 三峡大学学报(自然科学版),2013,35(6):12-15+58.

[3] 俞亭超,张土乔,毛根海,等. 预测城市用水量的人工神经网络模型研究[J]. 浙江大学学报(工学版), 2004, 38(9): 55-60.

[4] 崔东文.加权平均集成神经网络模型在城市需水预测中的应用[J]. 水资源保护,2014,30(2):27-32+45.

[5] 王弘宇,马 放,杨 开,等. 灰色新陈代谢GM(1,1)模型在中长期城市需水量预测中的应用研究[J]. 武汉大学学报(工学版), 2004, 37(6): 32-35.

[6] 王春娟,冯利华,罗 伟,等.主成分回归在需水预测中的应用[J]. 水资源与水工程学报,2013,24(1):50-53.

[7] 王 盼,陆宝宏,张瀚文,等. 基于随机森林模型的需水预测模型及其应用[J]. 水资源保护, 2014, 30(1): 34-37,89.

[8] 何 斌,张澎辉,梁国华,等. 基于BP神经网络的场次洪水河道沙量预报[J]. 南水北调与水利科技,2015,13(3):406-408+416.

[9] 崔吉峰,乞建勋,杨尚东. 基于粒子群改进BP神经网络的组合预测模型及其应用[J]. 中南大学学报(自然科学版),2009,40(1):190-194.

[10] 臧冬伟,陆宝宏,朱从飞,等. 基于灰色关联分析的GA-BP网络需水预测模型研究[J]. 水电能源科学,2015,33(7):39-42+6.

[11] 舒媛媛,周维博,刘 雷,等. 基于主成分分析的BP神经网络在延安市需水预测中的应用[J]. 水资源与水工程学报,2012,23(6):172-175.

[12] 杨 婷,魏晓妹,胡国杰,等. 灰色BP神经网络模型在民勤盆地地下水埋深动态预测中的应用[J]. 干旱地区农业研究,2011,29(2):204-208.

[13] 张以帅,赖惠鸽,李 勇,等. 基于MEA优化BP神经网络的天然气短期负荷预测[J]. 自动化与仪表,2016,31(5):15-19.

[14] 赵瑞勇,周新志. 基于MEA-BP的微波加热褐煤温度预测[J]. 传感器与微系统，2016，35(10): 43-45+48.

[15] 杜 晓. 基于MEA-BP模型的股票预测研究[D]. 兰州：兰州大学,2015.

[16] 吴 伟,郭军巧,安淑一,等. 使用思维进化算法优化的神经网络建立肾综合征出血热预测模型[J]. 中国卫生统计,2016,33(1):27-30.

[17] 王艳菊,王 珏,吴泽宁,等. 基于灰色关联分析的支持向量机需水预测研究[J]. 节水灌溉,2010(10):49-52.