基于G-H copula函数的秦淮河流域洪水风险分析
高玉琴, 叶 柳, 赖丽娟
(河海大学 水利水电学院, 江苏 南京 210098)
1 研究背景
随着洪水风险问题研究越来越深入,从多角度对洪水进行定义和描述的多变量联合风险分析方法已经越来越受到关注。Copula函数因为其构造灵活,计算简单,且不限制边际分布类型等优点而备受青睐,已被大量应用于降雨、干旱等多变量联合概率分析以及洪水遭遇、多站点多水文区的洪水联合风险分析等水文领域。
二维copula研究理论及应用已经相对成熟,三维及更高维数copula函数由于维数的拓展和各变量间相依性不对等,理论更为复杂。涂新军等[1]应用Archimedean copula进行了滨海城市降雨和潮位联合分布的模拟和设计,并对比基于二次重现期的设计值和传统联合重现期设计值,证明二次重现期设计更为安全。黄锦林等[2]基于最大熵-copula方法分析降雨和潮位关联性,得出多种雨潮设计值遭遇组合风险概率。闫宝伟等[3]采用clayton copula构建长江和清江峰现时间与量级二维分布,进而探索洪水遭遇风险特性。Chowdhary等[4]详细论述了copula函数类型优选方法并介绍其在二元洪水频率计算中的应用。Zhang等[5]利用Archimedean copula函数研究了降雨强度、径流深、降雨历时两两变量间的联合分布,并分析相依性和边缘分布对结果的影响;Reddy等[6]具体阐述了二维洪水变量频率分析的步骤流程以及用Monte Carlo数值模拟法判断copula拟合程度的方法。在三维copula方面,陈子燊等[7]分析洪量、历时、洪峰三变量联合分布及各种重现期的设计分位数;侯芸芸等[8]考虑洪峰、洪量和历时之间的相依性,构造了三维对称性Archimedean copula函数,探讨洪水联合概率分布和条件概率分布;Ganguli等[9]利用多种联结函数类型描述洪峰流量、洪量、洪水历时的两变量、三变量联合概率分布,并讨论了两种重现期特性和尾部相关性。
基于次洪变量,如时段洪量、洪峰、峰现时间、洪水历时等进行的联合分布研究以及降雨和洪水、降雨和潮位相关性研究较多,但是目前从流域洪水风险角度将影响风险大小的洪量、洪峰流量和洪水位三者进行联合分析的研究较少。本文以秦淮河流域为研究区域,选取P-Ⅲ、 GEV分布和两参数对数正态分布Ln2描述洪水风险变量洪量、洪峰和洪水位的边际分布类型,利用G-H copula构建二维和三维风险评价模型,计算不同组合洪水事件的联合重现期、条件重现期以及二次重现期,为区域工程设计和风险评估工作提供依据。
2 数据与方法
2.1 研究区域与数据来源
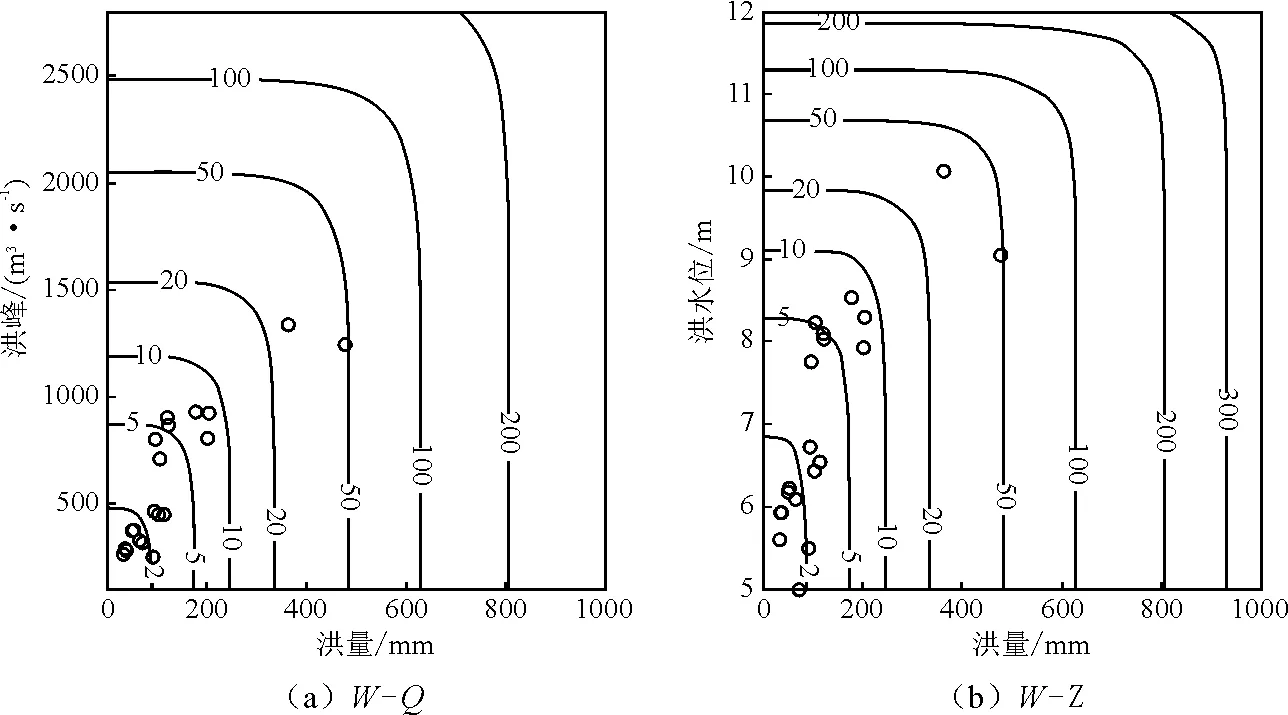
秦淮河流域地处长江下游地区,面积为2 631 km2,干流长度为34 km,属于亚热带湿润、半湿润季风气候区,汛期雨量充沛,洪水灾害频繁。根据1986-2006年流域出口处秦淮新河和武定门闸水文站的日流量资料和1986-2006年东山站站前水位资料,采用年最大值选样法(AM),基于袁玉等[10]根据秦淮河流域水文、气象、降雨等资料建立的HEC-HMS水文模型及HEC-RAS水力模型,模拟年最大洪水事件演进到东山站前的水位。洪量、洪峰均为秦淮新河闸与武定闸两处叠加值,以全流域径流深的形式表示洪量,洪水位为东山站点前水位。
2.2 G-H copula函数
G-H Copula是Archimedean copula函数的一种,通常用于描述正相关和上尾相关性随机变量[11],当维数为2和3时,G-H Copula表达式分别为:
C(u1,u2)=exp{-[(-ln(u1))θ+
(-ln(u2))θ]1/θ}θ∈(1,∞)
(1)
C(u1,u2,u3)=exp{-[(-ln(u1))θ+(-ln(u2))θ+
(-ln(u3))θ]1/θ}θ∈(1,∞)
(2)
2.3 参数估计与拟合优度检验
核密度估计、相关性指标法、IFM法、EML法等都可进行copula参数估计。对于二维ArchimedeanCopula常用相关性指标法,根据τ和θ的关系由τ来估计。但三维copula显然不能使用相关性指标法估算参数,本研究采用IFM法。
为验证Copula和实测样本经验累积概率之间的拟合程度,需对构建的模型进行拟合优度检验。常见检验方法有RMSE法、AIC法和BIC法。本文采用均方根误差法:
(3)
式中:Femp为经验概率值;C为理论概率值;n为系列长度。RMSE值越小,拟合情况越好。三维经验频率的计算公式为:
(4)
式中:njkl为同时满足Xi1≤xi1、Xi2≤xi2、Xi3≤xi3时的联合观测个数。
实施国土资源所巡察“五个三”行动计划 整体提升基层国土资源一线工作水平(殷金兰) ..........................3-12
2.4 重现期
洪水特征变量的联合概率分布、条件概率分布以及相应的重现期计算是水文频率分析的重要成果,超过某一重现期设计阈值的洪水事件被定义为危险事件。传统同现重现期和联合重现期对洪水事件安全和危险域识别存在局限性,有可能发生识别错误的情况,造成风险管理和工程设计的成本增加或风险抵抗能力不足,而Kendall重现期能在同一临界水平下对任意洪水组合的安全和危险域识别保持一致性[12-13]。本文将Kendall重现期应用到多因素风险分析中,并与传统重现期进行对比。传统重现期定义见参考文献[7],在此不再赘述。
Kendall重现期,又称二次重现期,根据Genest和Rivest定义的Kendall分布函数,对于给定的t,通过求解特征量联合分布C小于或等于t的累积概率将多维变量信息投射为一维。Kendall重现期定义为:
(5)
式中:KC为Kendall分布函数,KC(t)=P(C(u1,u2)≤t))。对于Archimedean copula函数族中的二维G-H copula,KC可以表示为:
(6)
对于三维G-H copula, 可以表示为:
(7)
3 结果与讨论
3.1 相依性度量和边际分布
采用Pearson′γ,Spearman′ρ和Kendall′τ进行洪量和洪峰、洪量和洪水位,洪峰和洪水位两两变量间的相依性度量,并在括号中给出显著性水平为0.05时对应的P值,计算结果如表1。由表1可以看出,变量之间的相关性均较大,表明洪量(W)、洪峰(Q)、洪水位(Z)之间存在较强相关性,因而可进行洪水变量间的联合概率特性分析。

表1 变量之间的相依性
选取P-Ⅲ、GEV和ln2描述变量的边际分布,边际分布概率密度表达式见文献[14]。采用最大似然法估计参数并通过KS检验判断拟合优度,KS统计量值越小,拟合情况越好;P值越大,则有越大可能接受该分布。表2为洪水特征变量边际分布参数和拟合优度检验结果。由表2可知,3种边际分布均能被接受,基于最小KS统计量分别选择GEV,ln2和P-Ⅲ分布为洪量、洪峰、洪水位的边际分布。绘制变量边际分布经验频率与理论频率关系图,如图1所示,由图1可以看出,点据分布在1∶1斜线附近,证明拟合程度较好。

表2 边际分布参数估计和拟合优度检验
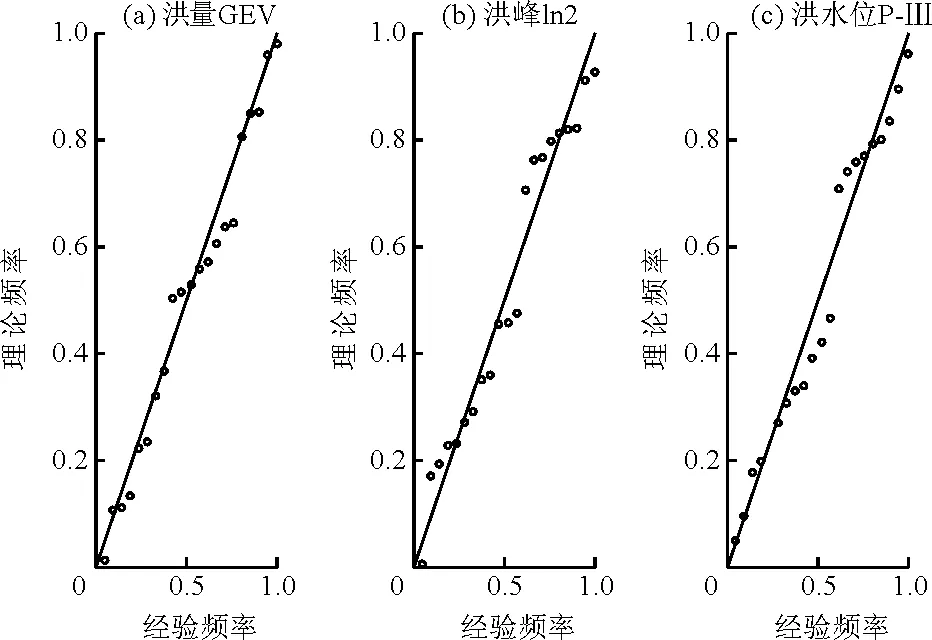
图1 边际分布拟合图
3.2 联合分布函数
采用G-HCopula描述二维变量间相依结构,用IFM法估计参数,计算得洪量洪峰、洪量洪水位和洪峰洪水位二维联合分布函数的参数分别为3.1231、2.8655、6.7281,对应的均方根误差RMSE分别为0.0090、0.0106、0.0149。以相关性最强的洪峰和洪水位为主进行二维变量洪水风险分析,探讨其联合重现期、同现重现期和Kendall重现期性质,并分析洪峰不超过一定重现期时洪水位风险率。
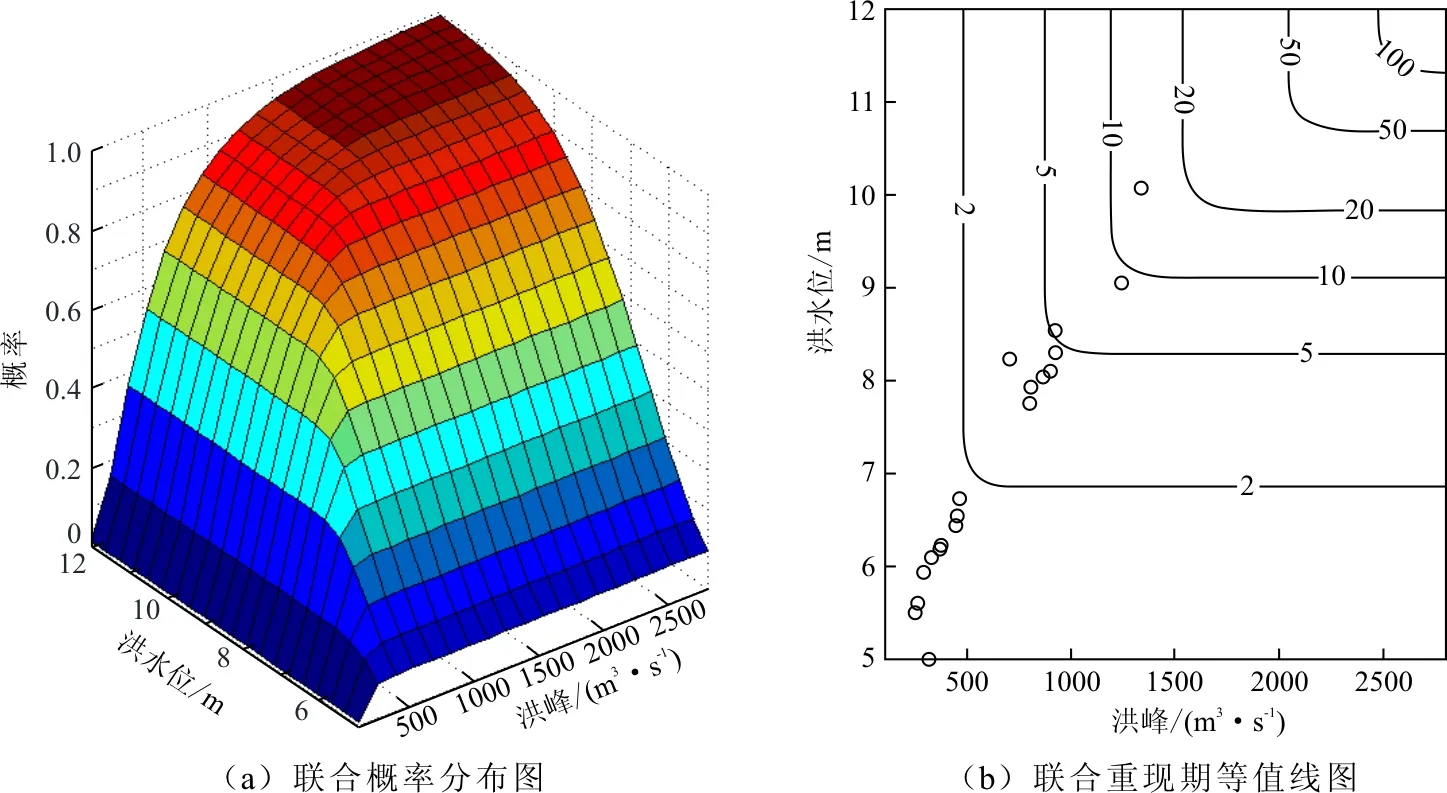
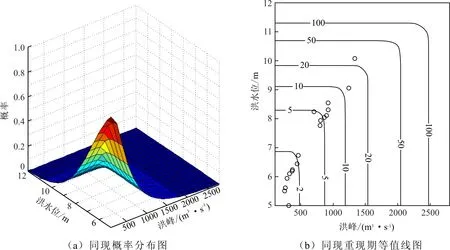
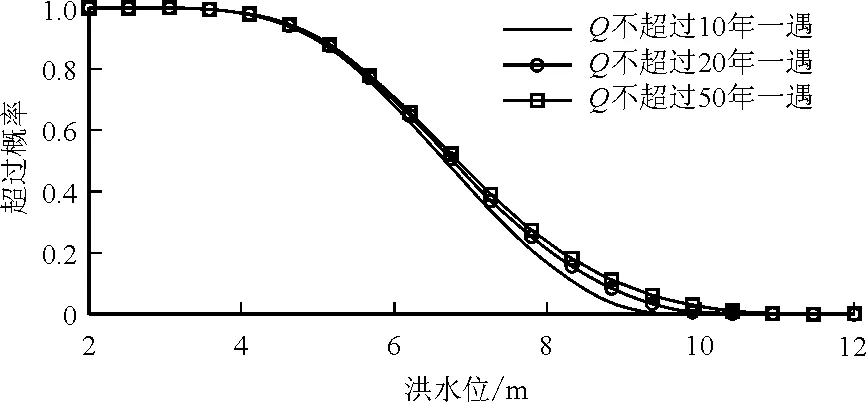
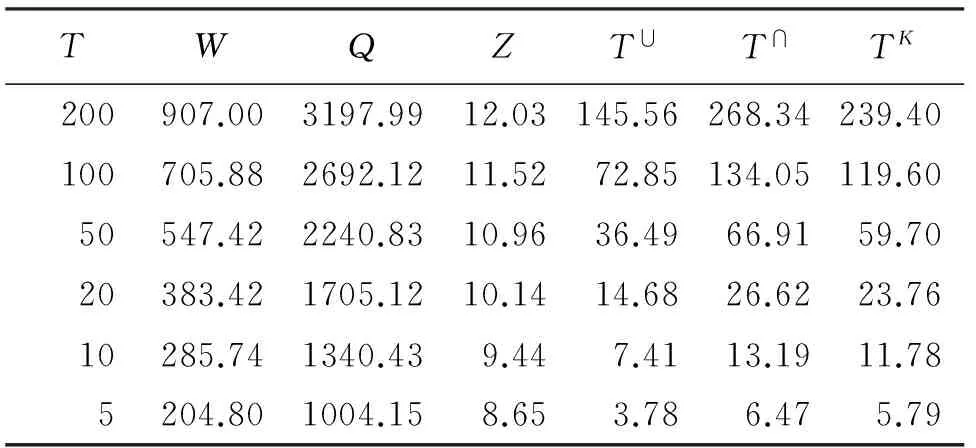
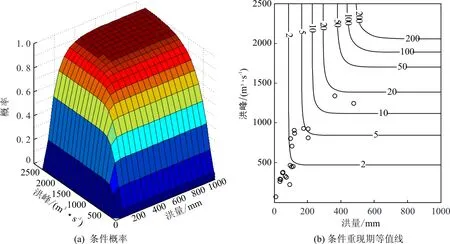
分别计算洪峰和洪水位在5~200a重现期内的联合T∪,同现T∩和二次重现期TK值,并给出单变量条件下的设计值,见表3。Q-Z二维分布条件下,相较于单因素重现期,T∪更小,T∩更大,而Kendall重现期在T∪和T∩之间且与单因素重现期误差最小,大小顺序为T∪ 绘制洪峰和洪水位的概率分布图和相应的重现期等值线图,并加入实测数据进行对比,如图2和图3。由图2、3可知,Q-Z最大联合重现期约为15 a,最大同现重现期则超过20 a。可计算任意Q-Z组合事件的重现期,如发生50年一遇洪峰和20年一遇洪水位的联合重现期和同现重现期分别为19.99 a和50.03 a。绘制W-Q和W-Z的同现重现期等值线图,如图4。Q-Z的同现重现期较W-Q和W-Z的同现重现期小,说明秦淮河流域洪峰和洪水位同现风险率最大。 绘制洪峰不超过10、20、50年一遇时洪水位的超越概率FZ|Q=P(Z>z|Q≤q),如图5。洪峰不超过10、20、50年一遇设计值时,洪水位超过5年一遇 (8.29m)的概率分别为0.1113、0.1579、0.1837。给定某一洪水位阈值,洪峰量级越小,洪水位风险率越小,即洪峰量级小,洪水位也越不容易超过该阈值。 表3 单变量设计值及各种重现期 图2 Q-Z联合概率分布图及联合重现期等值线图 图3 Q-Z同现概率分布图及同现重现期等值线图 图4 W-Q、W-Z同现重现期等值线图 图5 洪峰不超过某一重现期时洪水位风险率 按照公式(3),通过各变量边缘分布构建三维G-Hcopula模型,用IFM法由洪水资料估计参数,计算得出θ=3.4472,用均方根误差法对G-Hcopula函数进行拟合优度检验,RMSE=0.0147,误差值较小 ,满足拟合要求。分别计算洪量、洪峰和洪水位在5~200a重现期内的T∪、T∩、TK值和3变量情况下的同频率设计值,如表4。由表4可以看出,3变量同频率设计值大于相应单变量设计值,洪量洪峰洪水位三维分布条件下,各重现期大小排列依然是T∪ 因子后,传统重现期、二次重现期与单因素重现期之间的差值明显增大,风险率变化幅度增大。 由《南京城市防洪规划报告(2011-2020年)》可知,东山站20年一遇规划水位为10.8m,绘制洪水位不超过10.8m条件下洪量洪峰的条件概率FWQ|Z=P(W≤w,Q≤q|Z≤10.8)及相应的重现期等值线图,如图6。洪水位不超过10.8m条件下,实测资料中大部分W-Q联合重现期小于或等于5a,说明较高洪水位条件下,洪量和洪峰的任意一个超过风险率较大。 表4 3变量同频率设计值及各种重现期 图6 Z≤10.8 m时W-Q条件概率分布及条件重现期等值线 以秦淮河流域为例,基于边际分布拟合,选择广义极值分布GEV,对数正态分布ln2和P-Ⅲ分布作为洪量(W)、洪峰(Q)、洪水位(Z)的边际分布类型,构建二维和三维G-Hcopula洪水风险评价模型,并计算多变量联合概率、条件概率以及传统重现期和Kendall重现期,得出了以下结论: (1)相较于单因素重现期,Q-Z二维T∪更小,T∩更大,而Kendall重现期在两者之间且与单因素重现期误差最小。 (2)Q-Z的T∪小于W-Q和W-Z的T∩,说明秦淮河流域洪峰和洪水位同现风险率最大;Q-Z在二维分布条件下,洪峰量级越小,则洪水位风险率越小。 (3)计算3变量联合分布和限制洪水位条件下W-Q联合概率分布,3变量情况下的同频率设计值大于相应单变量设计值,3变量传统重现期、Kendall重现期与单因素重现期之间的差值明显增大。 [1] 涂新军,杜奕良,陈晓宏,等. 滨海城市雨潮遭遇联合分布模拟与设计[J]. 水科学进展,2017,28(1):49-58. [2] 黄锦林,范嘉炜,唐造造. 基于最大熵-Copula方法的降雨潮位关联性分析——以广州为例[J]. 灾害学,2017,32(1):65-71. [3] 闫宝伟,郭生练,陈 璐,等. 长江和清江洪水遭遇风险分析[J]. 水利学报,2010,41(5):553-559. [4]CHOWDHARYH,ESCOBARLA,SINGHVP.Identificationofsuitablecopulasforbivariatefrequencyanalysisoffloodpeakandfloodvolumedata[J].HydrologyResearch,2011, 42(2-3):193. [5]ZHANGL,SINGHVP.BivariaterainfallfrequencydistributionsusingArchimedeancopulas[J].JournalofHydrology,2007, 332(1):93-109. [6]REDDYMJ,GANGULIP.Bivariatefloodfrequencyanalysisofuppergodavaririverflowsusingarchimedeancopulas[J].WaterResourcesManagement,2012, 26(14):3995-4018. [7] 陈子燊,黄 强,刘曾美. 基于非对称ArchimedeanCopula的三变量洪水风险评估[J]. 水科学进展,2016,27(5):763-771. [8] 侯芸芸,宋松柏,赵丽娜,等. 基于Copula函数的3变量洪水频率研究[J]. 西北农林科技大学学报(自然科学版),2010,38(2):219-228. [9]GANGULIP,REDDYMJ.Probabilisticassessmentoffloodrisksusingtrivariatecopulas[J].Theoretical&AppliedClimatology, 2013,111(1-2):341-360. [10] 袁 玉,高玉琴,吴 锡. 基于HEC_HMS水文模型的秦淮河流域圩垸式防洪模式洪水模拟[J]. 三峡大学学报(自然科学版),2015,37(5):34-39. [11] 潘璀林,陈子燊. 基于GHCopula的韩江水文干旱联合概率分布研究[J]. 中山大学学报(自然科学版),2015,54(1):110-115. [12] 黄 强,陈子燊. 基于二次重现期的多变量洪水风险评估[J]. 湖泊科学,2015,27(2):352-360. [13] 范嘉炜,黄锦林. 基于Kendall重现期的降雨潮位风险分析[J]. 水电能源科学,2017,35(5):21-24+20. [14] 高玉琴,陈钇西,赵立梅,等. 秦淮河流域不同频率降雨联合概率分析[J]. 水电能源科学,2016,34(3):1-5+23.
4 结 论

