基于卷积神经网络的随机梯度下降算法

王功鹏，段 萌，牛常勇

(郑州大学 信息工程学院，河南 郑州 450001)

0 引 言

卷积神经网络(以下简称CNN)是在神经网络的基础上进行改造的深层网络，是目前语音分析以及物体识别等领域使用最广的网络结构[1]。CNN中使用最广泛的优化算法当属SGD(stochastic gradient descent)算法，SGD算法的关键在于学习率η，η如果设置不当将会直接影响SGD的效果。针对学习率的研究，文献[2]提出了一种学习率自适应递减算法，但是其学习率是严格递减的，在训练后期学习率会变得非常小。为了使得学习率能更好适应SGD算法以提高SGD算法的效率，本文提出了一种用于SGD的学习率自适应更新算法，该算法的主要思想是随着迭代的进行，根据不同的迭代次数周期性的将学习率进行更新，使得学习率能更好地适应SGD算法。

目前CNN中常用的激活函数为Relu(rectified linear units)函数。然而，在Relu函数中的阈值为负的神经元处于抑制的状态[3]，针对Relu函数的这种缺陷，文献[4]提出了一种改进的激活函数Leaky Relu。该激活函数在阈值大于零部分的处理与Relu一致，但是在小于零的部分的处理则是将这些阈值乘以一个很小的数值，而不是直接压缩至零。这样既重新修正了数据的分布同时又避免了网络梯度的消失，这也是近年来国内外研究者常用的激活函数。目前针对CNN国外的研究者提出了许多的改进，如国外研究者提出了许多新的激活函数如PReLU(parametric retified linear unit)[5]、RReLU(randomized rectified linear unit)等激活函数，目前国外最新的研究还提出在训练过程中使用批规范化来提高训练速度[6]。本文将分别对比采用Leaky Relu与Relu作为激活函数的CNN的实验结果。

本文也将采用上述提出的学习率自适应更新算法的SGD和Leaky Relu进行结合在标准数据集上进行分类识别测试，并且与Relu和学习率非自适应的SGD进行比较。

1 卷积神经网络概述

1.1 卷积神经网络基本结构

卷积神经网络(CNN)是在前馈神经网络基础上进行升级改造的深层神经网络，每个神经元都只与邻近的局部神经元相互作用。CNN有三大特性分别为局部感知野、权值共享和降采样[7,8]。局部感知野使网络提取局部特征的能力大大增强。权值共享可以显著的减少网络中的参数，很大程度地降低了网络计算的复杂度。权值共享和降采样的结合使得网络的计算复杂度显著下降，这也正是CNN优于其它算法的显著特征，正是这些特性使得CNN迅速得到普及。CNN在图像分类和语音识别中使用最为广泛，大部分计算机视觉系统都将它作为核心技术。目前国内也有很多基于CNN的成功的研究成果如手势识别[9]和用于情感识别平台[10]等。

卷积运算实际是一种对图像元素的矩阵变换，它的输入层是通过一个W*W大小的卷积核与上一层输入的一小部分进行连接并进行卷积运算，然后提取该区域的局部特征。如此就减少了网络中的参数使得网络的计算复杂度显著降低，同时也提高了网络的训练性能。卷积运算公式如下

(1)

通过卷积运算提取图像特征后，下一步就是从这些获得的特征中去进行分类处理。降采样层主要作用是对通过卷积核提取到的特征进行降维抽样处理。目前CNN中常用的池化操作有最大池化、均值池化和随机池化。本文所选择最大池化作为池化操作。经过池化操作后网络的维度就大幅地降低，同时也降低了过拟合发生的机率。降采样公式如下所示

(2)

其中，降采样函数用bool(·)表示。在对输入图像中不同区域的n*n块的全部像素进行求和运算时，降采样函数可以将图像整体缩小了n*n倍。经过降采样获得重新规划的值后，将该值与偏执系数β相乘，最后激活函数再将该值输出。

本文中在每一个卷积层后降采样层前都会添加Relu或者Leaky Relu函数作为激活函数。同时为了防止过拟合的发生将会结合Dropout[11]一起使用。CNN最后全连接层采用Softmax函数来作为回归函数对结果进行分类，Softmax回归模型针对于多分类问题，它也是CNN常用的分类器。另外选择合适的优化算法来学习模型参数，通过Softmax回归函数计算出顶层损失值，再使用优化算法学习模型参数。本文选择学习率非自适应的SGD算法与本文提出的使用学习率自适应更新算法的SGD作为优化算法。

1.2 Leaky Relu激活函数及其特性

Relu激活函数是CNN中使用最广的激活函数。Relu激活函数具有如下优势：解决梯度消失问题和提高网络的训练速度[4]。综上所述，选择计算复杂度更低计算速度更快的Relu作为CNN的激活函数更为合适。但是它同样有很大的缺陷，Relu激活函数的表达式为：f(x)=max(0,x)，x表示网络输入阈值，f(x)表示的是网络输出值。从表达式可以看出它只保留了大于零的部分的阈值，而简单的将小于零的部分的阈值置为零，因而该激活函数具有了稀疏表达能力，但是同时该激活函数中阈值为负的神经元处于抑制的状态，这些神经元的权值也不会再通过反向传播算法进行更新。针对这种缺陷本文提出采用LeakyRelu激活函数作为CNN的激活函数。

LeakyRelu激活函数对应的公式如下

(3)

式中:xi代表激活函数的输入值，yi代表的是激活函数输出值。α代表的是一个范围为(0,1)之间的数值斜率，在实际使用过程中α会根据先验经验值进行设定。文献[12]通过大量的实验验证α的值在0.1至0.5之间效果达到最佳，本文通过大量实验后将其值设置为0.15。

从式(3)中可以看出，LeakyRelu激活函数将阈值为负的神经元与一个很小的数值向乘，如此阈值为负的神经元不会被丢弃同时这些的神经元信息也得到了保留。

2 SGD算法

2.1 SGD算法原理

在机器学习中，对于大多数的监督学习模型，为了得到最优的权值，需对模型创建代价损失函数，然后选择合适的优化算法以得到最小的函数损失值。梯度下降算法是目前使用最广的优化算法。它的核心思想是：要计算出最小的函数损失值，必须先计算出损失函数的梯度，然后按照梯度的方向使函数损失值逐渐减少，通过对权值的不断更新调整，使得函数损失值达到最小，从而获得最优解。SGD算法是一个基于梯度下降的改进算法，SGD每次随机选择一个样本来迭代更新一次，而不是针对所有的样本。因此该算法明显的降低了计算量。SGD具有训练速度快易收敛等特性，也是最受国内外研究者青睐的优化算法。SGD相关的公式如下

(4)

(5)

φ:=φ-η▽φh(φ)

(6)

式中，φ代表网络参数权值，▽φ表示的是梯度，h(φ)代表损失函数，g(φ)代表目标函数，yi代表第i个样本的样本值，m表示的是整个迭代进行的总次数，η表示梯度下降中的步长即学习率，j表示的CNN中参数的总数目。正如上文所描述的学习率对梯度下降算法至关重要，如果η设置的过小则会需要多次迭代才能找到最优解且会降低网络的收敛速度，甚至可能出现陷入到局部最优解中停滞不前的情况。如果增大学习率，虽然会加快CNN的训练速度，但是同时也会加大了跳过最优解的机率，CNN可能出现找不到最优解的情况[13]。由此可以看出η是决定梯度下降算法是否有效的关键因素。为了使学习率更好地适应SGD，本文针对学习率提出了一种基于SGD的学习率自适应更新算法。

2.2 基于SGD的学习率自适应更新算法

目前较为流行的CNN结构中都将冲量添加到SGD实现方式中，冲量的作用是为了防止CNN在最小损失值点而继续进行迭代训练不能停止的情况发生[14]。本文在CNN中的SGD也添加冲量并将其设置为0.9。为了克服SGD中学习率选择的困难，本文提出了一种让学习率自适应SGD的学习率自适应更新算法，通过该算法获得的学习率来更加适应网络的训练。与使用学习率非自适应的SGD相比使用该算法的SGD解决了学习率设置不当而跳过最优解而产生动荡的问题。算法描述见表1。

表1就是本文提出的SGD学习率更新算法，但是为了防止η递减的过快本文设置了上述的学习率更新规则1和学习率更新规则2两种学习率更新规则。常数σ是防止随着迭代的进行η逐渐减小以至于过小而失去作用而设置的。按照本文提出的学习率更新算法每进行一次迭代后相应的更新学习率η，这样就做到了学习率的更新。随着迭代的进行，函数损失值逐渐减小，应适当的减小学习率。故本文算法中学习率呈现整体梯形下降趋势，但并不是严格下降，而是在一定迭代区间内周期性下降，采用周期性下降的方式可以使得相同的学习率参与更多的训练，使得学习率得到充分的使用。随着迭代的进行学习率衰减幅度也逐渐减

表1 SGD学习率自适应更新算法

小，这样可以防止因学习率减小的过快而造成网络收敛变慢情况的发生。该算法具有通用性对所有的SGD算法都适用。其中本文学习率自适应更新算法中学习率随迭代次数变化如图1所示。

图1 本文学习率变化曲线

3 实验与结果分析

3.1 实验平台和数据

实验选取的数据集为Yann LeCun建立的数字手写字符体MNIST，Alex Krizhevsky等收集建立的CIFAR-10[15]的一般物体图像数据集和CIFAR-100数据集，其中CIFAR-10共有60 000张尺寸为32*32的真彩色图片，共有10种类别。CIFAR-100数据集与CIFAR-10数据集类似不过它包含了20种大类和100种小类别。

实验平台选择的是Amazon提供的云计算服务EC2机型，操作系统为Linux Ubuntu 14.04，选择的GPU型号为GRID K520，可用显存大小为8 GB。采用了NVIDIA提供的计算加速方案。

实验数据集，见表2。

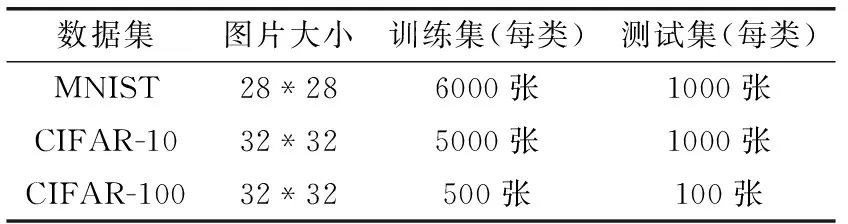
表2 实验数据集

3.2 数据集网络结构参数

对于3个数据集，本文设计了不同的网络结构。表3给出了用于3个数据集的网络结构参数。

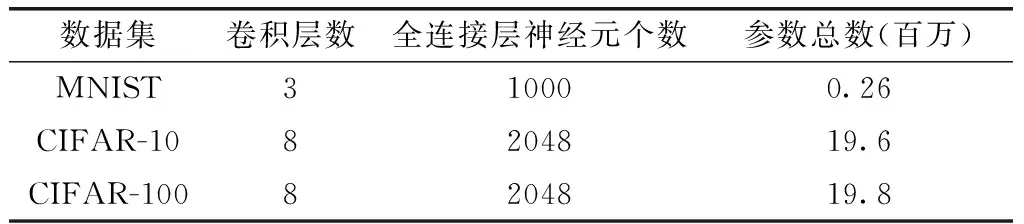
表3 3个数据集网络结构参数

3.3 实验结果分析

评价一个算法优劣有很多种的标准如交叉验证集正确率、训练集正确率以及优化算法的收敛性[16]。本文选取上述3种标准作为本文算法评价的标准。本文中的实验在MNIST，CIFAR-10和CIFAR-100数据集各进行了150次迭代。表4～表6给出了不同CNN在各个数据集独立运行20次后取平均值的实验结果。其中Relu与Leaky Relu分别表示激活函数采用Relu与Leaky Relu，优化算法采用固定学习率为0.01非自适应的SGD的网络。MSGD Relu与MSGD Leaky Relu分别表示激活函数采用Relu与Leaky

Relu，优化算法为采用本文提出的学习率自适应更新算法的SGD的网络。

表4 MNIST数据集的实验结果

表5 CIFAR-10数据集的实验结果

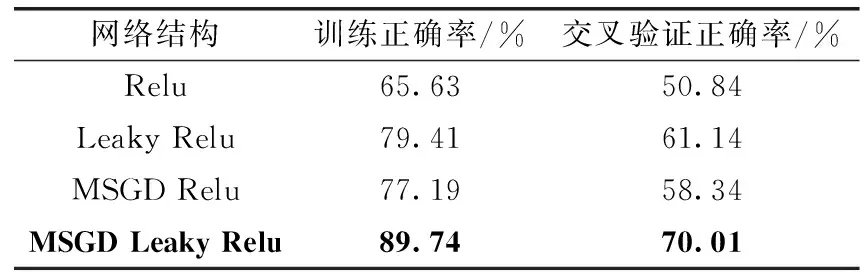
表6 CIFAR-100数据集的实验结果

从上述的实验结果中可以看出，在3个数据集上，在相同优化算法下使用Leaky Relu激活函数的网络正确率要高于使用Relu激活函数的网络。在相同激活函数下优化算法采用本文的学习率自适应更新算法的SGD的网络的训练和验证正确率也要高于采用学习率非自适应的SGD的网络。从实验结果中可以看出，采用Leaky Relu作为激活函数，以本文的学习率自适应更新算法的SGD作为优化算法相结合可以进一步提高网络的训练和验证正确率。

其中各个网络在3个数据集上训练和验证和收敛曲线如图2～图4所示。train_loss表示训练函数损失值，val_loss表示验证函数损失值，Epochs表示迭代次数。

图2 不同网络在MNIST数据集上的收敛曲线

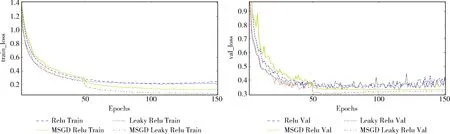
图3 不同网络在CIFAR-10数据集上的收敛曲线

图4 不同网络在CIFAR-100数据集上的收敛曲线

从图2～图4实验结果可以得出结论，使用Leaky Relu作为激活函数的网络目标函数的损失值明显小于使用Relu作为激活函数的网络。当优化算法采用本文的学习率自适应更新算法的SGD的网络能更快的收敛，训练损失值和验证损失值趋于平稳不再波动。网络的收敛性明显的优于学习率非自适应的SGD算法。

从图4中可以看出在CIFAR-100数据集上激活函数采用Relu的网络的函数损失值最后呈现上升趋势。相反激活函数采用Leaky Relu，优化算法采用本文的学习率自适应更新算法的SGD的网络能更好的训练下去。且采用本文的学习率更新算法的SGD和Leaky Relu激活函数相结合的网络不仅具有更好的收敛性，而且训练函数损失值和验证函数损失值均小于其它网络，实验效果明显优于其它网络。

评估一个优化算法优劣的最可靠的依据就是看该优化算法是否收敛[16]，数据是否趋于稳定，参数是否达到了稳定值，是否还会出现周期性波动。实验结果表明，采用本文的学习率自适应更新算法的SGD的网络收敛性明显的好于其它网络。由此可以得出结论：本文提出的算法有效，能够提高SGD算法的效率。

4 结束语

针对CNN中Relu激活函数的不足，本文设计了采用Leaky Relu作为激活函数的CNN，同时也将CNN中传统的SGD算法进行了改良并提出了基于SGD的学习率自适应更新算法。3个数据集上的实验结果表明，以Leaky Relu作为激活函数的CNN实验结果要优于使用Relu作为激活函数的CNN。使用本文的学习率自适应更新算法的SGD在保证正确率的前提下，还可以加快网络的收敛。然而，本文的算法中的众多参数仍有许多改进的地方。在以后的工作中如何找到更优的参数，仍然需要反复的实验和测试。下一步，将本文中的算法用于普适物体识别中，用该算法去解决实际问题。

[1]Lu Hongtao,Zhang Qinchuan.Applications of deep convolutional neural network in computer vision[J].Journal of Data Acquisition and Processing,2016,31(1):1-17.

[2]Duchi J,Hazan E,Singer Y.Adaptive subgradient methods for online learning and stochastic optimization[J].Journal of Machine Learning Research,2011,12(7):257-269.

[3]Glauner PO.Deep convolutional neural networks for smile reco-gnition[J].IEEE/ACM Transactions on Audio Speech & Language Processing,2015,22(10):1533-1545.

[4]Maas AL,Hannun AY,Ng AY.Rectifier nonlinearities improve neural network acoustic models[C]//Proceedings of the 30th International Conference on Machine Learning,2013.

[5]He K,Zhang X,Ren S,et al.Delving deep into rectifiers:Surpassing human-level performance on imageNet classification[C]//IEEE International Conference on Computer Vision.IEEE,2015:1026-1034.

[6]Ioffe S,Szegedy C.Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]//International Conference on Machine Learning,2015:448-456.

[7]AlexKrizhevsky,IlyaSutskever,HintonGE.ImageNetclassificationwithdeepconvolutionalneuralnetworks[C]//AdvancesinNeuralInformationProcessingSystem.Cambridge:MITPress,2012:1097-1105.

[8]LiangM,HuX.Recurrentconvolutionalneuralnetworkforobjectrecognition[C]//IEEEConferenceonComputerVisionandPatternRecognition.IEEE,2015:3367-3375.

[9]CAIJuan,CAIJianyong,LIAOXiaodong,etal.Preliminarystudyonhandgesturerecognitionbasedonconvolutionalneuralnetwork[J].ComputerSystems&Applications,2015,24(4):113-117(inChinese).[蔡娟,蔡坚勇,廖晓东,等.基于卷积神经网络的手势识别初探[J].计算机系统应用,2015,24(4):113-117.]

[10]LINPingrong,HOUZhi,WENGuihua.Openplatformofemotionrecognitionbasedondeeplearning[J].ComputerEngineeringandDesign,2016,37(6):1510-1514(inChinese).[林平荣,侯志,文贵华.基于深度学习的情感识别开放平台[J].计算机工程与设计,2016,37(6):1510-1514.]

[11]SrivastavaN,HintonGE,KrizhevskyA,etal.Dropout:Asimplewaytopreventneuralnetworksfromoverfitting[J].JournalofMachineLearningResearch,2014,15(1):1929-1958.

[12]XuB,WangN,ChenT,etal.Empiricalevaluationofrectifiedactivationsinconvolutionnetwork[D].ICMLDeepLearn,2015:1-5.

[13]PoriaS,CambriaE,GelbukhA.Deepconvolutionalneuralnetworktextualfeaturesandmultiplekernellearningforutte-rance-levelmultimodalsentimentanalysis[C]//EmpiricalMethodsinNaturalLanguageProcessing,2015:2539-2544.

[14]SutskeverI,MartensJ,DahlG,HintonG.Ontheimportanceofinitializationandmomentumindeeplearning[C]//InternationalConferenceonMachineLearning,2013:1139-1147.

[15]DudikM,HarchaouiZ,MalickJ.Liftedcoordinatedescentforlearningwithtrace-normregularization[J].Aistats,2012,22(22):327-336.

[16]WANGChangsong,ZHAOXiang.Generalmethodforevalua-tingoptimizationalgorithmanditsapplication[J].JournalofComputerApplications,2010,30(A01):76-79(inChinese).[汪昌松,赵翔.评价优化算法的一般性方法及其应用[J].计算机应用,2010,30(A01):76-79].