基于NVH特性的汽车大修周期的确定与实现

林可春，吕 翱

（福建船政交通职业学院 汽车系，福建 福州 350007）

就单台车辆而言，车辆在使用过程中发生的现故障具有随机性和不可预知性。在同款车型的同批次车辆中，有些车辆在使用若干年后才出现问题，而有些则在使用几个月后便发生故障。 因此，概率统计概念及其指标测量方法常用于汽车维修管理。

1 可用度与维修度

对于可修复的系统，我们不仅关心其发生故障的可能性大小，而且关心其故障的数量，并且也对维修所需的时间感兴趣，这就是可用度和维修度[1-2]。

可用度的定义为：在任何时刻任务需要时车辆能够正常使用的概率。可用性与时间有关。如图1所示，图中的存贮、物流等耗时作为“非工作时间”。能工作时间和不能工作时间组成了预计总工作时间（TT），期中能工作时间又分为工作时间 （OT）和待命时间（ST）；不能工作时间由行政和后勤供应操作中使用的非维护时间（ALDT）和总维护时间（TMT）组成。计划外修理时间（TCM）和计划修理时间（TPM）构成了总修理时间（TMT）；而非维修时间（ALDT）通常包括在计划外和计划维修期间使用的非维修时间。由此，可以得到可用性A：

图1 汽车总工作时间历程的分解Figure 1 Decomposition of total working time of auto mobile

2 NVH特性下的汽车可用度的马尔科夫过程模型分析

2.1 马尔可夫过程的含义

马尔可夫过程是一个没有后效应的随机过程，对于状态离散、时间连续的马尔可夫过程可以表述为[3-4]：设这一随机过程中｛X（t）,t∈[0,∞）｝的状态空间为 E，任意的整数 m （m≥2）和 m 个时刻的 t1,t2,…,tm（0≤t1≤t2≤…≤tm），正数 s以及 i1,i2,…,im，满足以下条件：

则称为｛X（t）,t∈[0,∞）｝马尔可夫过程。

在（2）式中，如果 tm代表当前某一时刻，t1,t2,…,tm-1表示过去时刻，而tm+s为将来时刻，那么这个公式表明在tm+s时刻的状态仅仅取决于现在时刻tm存在的状态，而与过去时刻t1,t2,…,tm-1过程无关。（2）式中右边条件概率的形式为：

上式称为马尔可夫过程的转移概率函数，可记为pij（t，t+s），描述为马尔可夫过程由 t时刻经 s 时间之后由i状态变成j状态的概率。此时，转移概率函数可记为 pij（s），即

对于汽车在使用寿命期间中随时都有可能处于工作状态、故障状态或维修状态，这是一种随机现象。在汽车的使用寿命期间随机故障发生的过程则是马尔科夫过程[4]。

2.2 汽车NVH特性下的可用度马尔可夫过程模型

对于可修复的单部件系统，假设组件正常时工作，组件发生故障时执行修复，修复后投入使用，则组件寿命X服从参数λ的指数分布。

部件故障修理的时间Y服从参数指数μ分布，可表示为：

又因为维修与工作是独立事件，即：

0为当系统工作时，1为当系统维修时。

系统在时间t上可以处于工作状态的概率是：

处于维修状态的概率为：

单部件的四种可能状态的状态转移概率可以通过在Pij（△t）表示t时刻系统处于状态i时，经过△t后转变成状态j的状态转移概率来计算。

（l）系统在时间t处于工作状态，经△t后仍处于工作状态的转移概率 P00（△t）≈1-λ△t。

（2）系统在时间t处于故障状态，经△t后系统修复处于工作状态的转移概率P10（△t）μ△t。

（3）系统在时间t是工作状态，在△t之后，系统变成故障的转移概率 P01（△t）≈λ△t。

（4）系统在时间t处于故障状态，经过△t后系统仍然处于故障状态的概率 P11（△t）≈1-μ△t。

单部件系统的马尔可夫过程如图2所示.

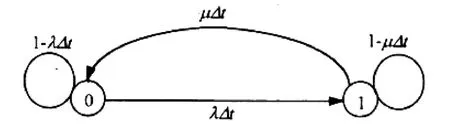
图2 单部件系统马尔可夫过程Figure 2 Markov process of single component system

由全概率公式知：

由式（7）和（8）推导得：

由系统可用度的概念得：

对于可修复串联系统，可分为n个相同部件的串联情况和n个不同部件的串联情况两种。当n个串联部件相同时，若给定初始条件为：（P0（0）,P1（0））=（1,0）。推导得系统的可用度为：

若已知汽车的失效率λ和维修率μ，则可由公式（10）或公式（11）算出在任一时刻汽车的可用度，某段时间内 A（t）的平均值为：

Am（t）称为一段时间的平均可用度。当t→∞时称为稳态可用度，记为：

将式（10）代入得：

在随机故障期间，失效率λ的倒数称之为平均故障间隔时间（MTBF），维修率μ的倒数则是修复所需的时间，即平均修复时间（MTTR），此时公式（13）为：

3 以最大可用度为目标的汽车最佳大修周期的诊断及仿真模拟

3.1 以最大可用度为目标的汽车最佳大修周期的诊断

借助于计算机仿真方法可以求解汽车发动机任一时刻的可用度，并且用最大可用度法解决最佳大修周期的问题。

当汽车故障率和维修率都不变时，系统在任何时间t处于可操作状态的概率可以通过使用公式（10）确定。使用一般的分析方法很难解决系统的可用性问题，但可使用计算机模拟方法得出汽车发动机某一时刻的可用度，从而确定最佳检修周期。解题步骤如下：

（1）根据给定的分布函数进行故障摸拟采样

已知的失效分布函数F（t）是单调递增的连续分布函数，当F（t）的反函数存在时，设Z作为均匀分布在[0,1]上的随机变量，则

为服从F（t）分布函数的随机变量。因此，我们可以用Z产生的简单子样Z1,Z2,…,Zn来产生随机变量的抽样值。

当 F（t）服从威布尔分布时：

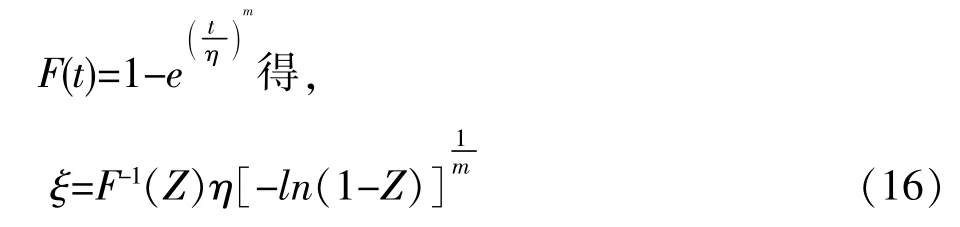
将[0,1]间的均匀随机抽样值代入式（16）得出故障所出现的时间服从F（t）随机变量的ξ随机抽样值。

（2）根据最大可用度得到汽车最佳维修周期

根据公式（11）计算汽车发动机可用度，若一个大修周期内出现K次故障，每次故障所需修理时间并不完全相等。一组从现场调查得到某型汽车发动机故障分布和事后维修所需时间如表1所示，拟合所得到故障修复时间的分布函数为：

故障发生的时间分布为：

表1 某型汽车发动机的故障分布和维修的时间分布Table 1 Distribution of faults and time distribution of maintenare for an automobile engine小时

虽然每次大修所需的时间不同，但离散不大，可以近似用对数正态分布描述，从现场调查我们得到大修修复时间如表1所示，拟合后服从以下分布：

表2 某型汽车发动机大修时间分布Table 2 Distribution of overhaul time of an automobile engine小时

1.3.2 最佳维修周期的Monte-Carlo仿真求解[5]

按照以下步骤执行最佳维修周期的计算机模拟。

步骤1：根据经验先假设一个大修周期T；

步骤2：根据故障分布函数，修复时间分布函数和大修时间分布函数对样本进行随机采样；

步骤3：计算在T周期内的随机故障数K，可以根据Monte-Carlo仿真求解最佳大修周期的关键步骤；

步骤4：把假设的大修周期数T和随机抽样得到的特殊随机数代入公式（10）就可以得到一个 A（t）值。 反复执行上述采样和计算可以获得稳定的可用度A（t）。

步骤5：改变假设的大修周期（均匀递增)Ti，重复上述步骤得出一系列与Ti对应的Ai值，绘制Ai—Ti曲线确定最佳大修周期。图3为计算机仿真计算框图。

图3 计算机仿真计算框图Figure 3 Computer simulation calculation block diagram

4 以最大效益为目标的汽车大修周期的诊断及实现

4.1 效益度的概念及其仿真模型

1）效益度的概念

效益度是汽车在给定时间内所能带来经济效益能力的概率。这个参数可以作为系统在任一时刻所处的状态下能否带来经济效益的量度。用累积收益参数x来代替可用度中的工作累积时间t，则效益度是收益x 的函数[6]。

V（x）表示到累积收益x时，系统可带来经济效益能力的概率。

V（x）可定义为：

x可称为广义的时间，例如说“到累积收效x时”就相当于说“到时刻t时”。

2）最大效益的度量方法

在使用汽车时，由于磨损、老化等原因，能源消耗和维护成本等成本指标将增加而带来负效益。汽车使用以创造经济效益为目的，选择最佳经济效益作为确定汽车检修周期的目标受到企业的欢迎。 参考汽车可用性的计算公式，给出了考虑车辆大修成本的效益度计算的公式：

式中，X为以累积效益为度量的大修周期，Ncxj为每次故障所需修理费用，Gpx为大修所花费的费用。若在一个大修周期内出现K次故障，则总的故障修理费累积为。

4.2 对汽车大修周期的仿真实现及结果分析

通过现场调查和对汽车振动系统的状态监测，得到表3、表4和表5三组数据，表3为汽车故障分布数据，表4为故障修理费用分布数据，表5为汽车大修费用分布数据，并且已知001#汽车在一个大修周期内的累积效益为145万元。

表3 汽车故障分布数据Table 3 Distribution data of vehicle foults

表4 故障修理费用分布数据Table 4 Distribution data of trouble shooting costs

表5 汽车大修费用分布数据Table 5 Distribution data of vehicle overhaulcosts

由仿真系统自动参数估计得到：

故障分布函数服从威布尔分布，有：

故障修复的费用分布函数服从威尔分布，可得到：

大修所需费用服从对数正态分布：

图4为三台汽车发动机按最大效益度仿真得到的V-X曲线。

图4 三台汽车的仿真V-X曲线Figure 4 Simulated V-X curve of three vehicles

5 小结

本文从汽车运行故障发生的随机特性，构建了NVH特性下的汽车可用度的马尔科夫过程模型，分析了随机情况对汽车可用度的影响。最后，分别以最大可用度和最大效益为目标完成了对汽车大修周期的确定，对汽车运营企业有一定参考作用。