基于差分进化算法的图像分割参数选择方法研究

朱必熙，张艳红

（福建幼儿师范高等专科学校 人文科学系，福建 福州 350013）

随着卫星发射技术、传感器技术与数据传输技术的发展，遥感图像的空间分辨率得到了很大的提高。高分辨率遥感图像的纹理、几何形状更加清晰、细致，但也使地物对应的图像更加复杂。对于如何从这些高分辨率图像提取有意义的信息存在不少挑战。基于对象的图像分析方法 （Object-Based Image Analysis，OBIA），是以图像对象作为分析单元，可充分利用地物光谱、纹理、几何和拓扑关系等多种特征的图像分析方法[1]。该方法近年在图像分析中得到快速的发展。图像分割获取的对象单元是OBIA的首要和关键步骤，直接影响后续基于图像对象分析与信息提取的精度。

鉴于图像分割对基于对象的图像分析方法的重要性，众多学者对图像分割进行了深入而广泛的研究，许多适用于遥感图像分割的算法被相继提出[2]。其中，基于区域生长的多尺度图像分割方法可以结合多种特征，进行多尺度的图像分割，被广泛应用于遥感图像的分割[3-6]。由于地物结构的复杂性、对地物本征尺度认识的不足、遥感图像量测尺度的不变性及图像分割算法中尺度参数与实际地物尺度之间联系的物理含义不确定性等原因，在实际应用中如何选择一个或多个合适的尺度进行图像的分割还是一个亟待深入研究和解决的问题。

本文通过将差分进化算法（Differential Evolution，简称DE）引入图像多尺度分割参数的选择，根据参考图与差异度准则选择最佳的分割参数，可在一定程度上减少分割参数选择的盲目性，这对于提高OBIA图像分类精度及其该方法的推广应用具有重要的意义。

1 研究方法

1.1 多尺度图像分割方法

本研究采用Baatz和 Schäpe 2000年提出的基于区域生长的多尺度图像分割算法作图像分割算法[4]。该算法根据区域虚拟合并前后的灰度特征标准差ΔStd、紧凑度ΔComp与光滑度ΔSmooth变化量，通过加权得到综合异质性测度HC，作为最终的合并准则测度，定义如式（1）。w1为灰度标准差变化量的权重，w2为形状因子中紧凑度的权重[6]。

标准差变化量ΔStd根据式（2）进行计算。其中，n为通道（波段）数，pi为第i通道的权重，am和Stdmi为合并后的区域大小和第i通道的标准差，a1和a2为合并的两个区域的大小，Std1i和Std2i为合并前两个区域第i通道的标准差。

合并前后区域的紧凑度变化量ΔComp定义如式（3）。am、a1和 a2为合并的两个区域的大小，lm、l1和 l2的为合并后及合并前的区域边界长度。如果紧凑度变化量小，两区域合并的可能性大。

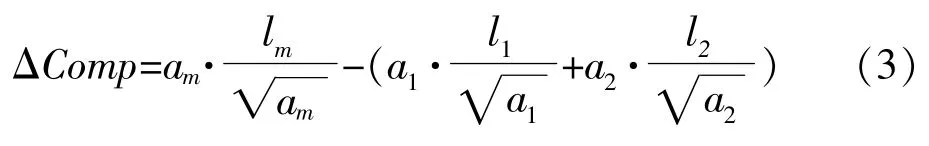
合并前后区域的光滑度变化量定义如式（4），和的含义同式（2），和的为合并后及合并前的区域边界长度，和的为合并后及合并前的区域外接矩形的周长。如果光滑度变化量小，两区域合并的可能性大。

1.2 差分进化算法

差分进化算法是一种基于随机并行搜索策略的启发式优化方法[7]。它对非线性不可微连续空间函数进行优化、具有向种群个体学习的能力，其比遗传算法、微粒群算法等其它进化算法更优越的性能[8]。差分进化算法保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了进化操作的复杂性。其特有的进化操作，使得其具有较强的全局收敛能力和鲁棒性，非常适合于求解一些复杂环境中的优化问题[9]。

差分进化算法根据需要求解的参数及问题求解空间随机产生初始种群，接着通过差分变异、修补与杂交等操作，产生中间个体（或称试验个体），然后通过选择操作生成下一代个体。算法通过不断迭代进化，引导收索向最优解逼近。算法的主要步骤如图1所示。

图1 差分进化算法的主要步骤Figure 1 Main steps of differential evolution algorithm

1.2.1 种群初始化

设NP代表种群数目，D为问题求解的维度，xi,j（0）表示初始种群（第0代）中第i个个体的第j维分量；与为第j维分量的最小与最大取值范围。则种群初始算子用式5和6进行。

式中 i=1,2,…,NP；j=1,2,…,D;rand（0,1）表示生成[0,1]的随机函数。

1.2.2 变异算子

差分进化算法通过将基向量加上因子缩放后的差分向量得到变异向量实现个体的变异。不同的基向量选择方式与不同的差分向量个数构成不同的差分变异算子。基向量的选择方式一般有随机选择和选择当代种群中最佳个体作为基向量两种方式；差分向量的个数一般为1或2。如式（7）的差分变异算子采取最佳个体作为基向量加上对一个差分向量进行缩放得到变异个体。

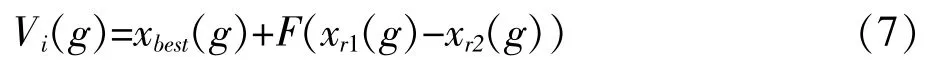
其中，xbest（g）为当前群体的最优个体向量；xi（g）为目标（父）向量；r1≠r2≠i为集合{1，2，…，NP}中随机选择的2互不相同的整数；xi（g）是变异向量；F为缩放因子或称变异概率，取值范围为[0,1+]差分算子是差分进化算法最重要的算子。目前的DE研究者设计了一些常用的变异算子，为了区分这些算子，采用“DE/a/b”来表示，DE表示差分进化算法；a代表基向量的选择方式 （用rand表示随机选择；best表示选择当代种群中最佳个体）；b表示差分向量的个数。比较常用的有变异算子可以参考文献[8]。

1.2.3 修补算子

变异后的个体可能落在解的搜索空间外，需采取修补手段，修补算子描述如式（8）。

1.2.4 杂交算子

DE算法通过杂交操作生成试验向量，杂交操作通过基准向量和变异向量进行，并采用离散杂交算子提高种群的多样性，常用的杂交算子有指数杂交算子和二项式杂交算子。指数杂交算子的交叉操作按式（9）进行。二项式杂交算子的操作可以参考文献十一[11]。

其中，〈l〉D表示对 D 取模运算，l是[1，D]之间的一个随机整数，整数L在1和D之间。

1.2.5 选择算子

DE算法根据目标向量和试验向量的适应度f（·）来选择最优个体，如果试验向量的适应度 f（ui（g））好于目标向量的适应度 f（xi（g）），保留试验向量，否则保留目标向量。选择算子可按式（10）进行描述。

1.3 分割对象的评价方法

基于参考对象的图像分割结果评价，通过计算分割结果与参考图对应区域的符合度来评价分割结果的优劣。符合度评价指标的设计直接影响分割结果优劣的选择。本研究采用Pont-Tuset和Marques提出的Precision and Recall （F）差异度指数作为评价指标[11]。该指标根据对参考对象和分割对象重叠情况的不同，将分割图像的像素分为四种区域，并据此定义分割对象与参考对象的差异度度量指标F。这四种区域的定义如图2所示，其中绿色线条包围的区域表示参考图班R的范围，红色线条包含的区域表示分割区域S的范围，tp表示正确分割的区域 （即tp=R∩S的部分），fp 表示过分割区域（即 fp=S-（R∩S）的部分），fn表示欠分割区域（即fn=R-（R∩S）的部分），剩余的部分表示不相关区域用tn表示，即tn=I-（R∪S），I表示整个图像。基于分割图班的正确分割率Rsk和基于参考图的正确分割率RRk，按式（11）计算，并根据式（12）计算差异度度量指标Fk。所有参考图的对应分割结果的差异度度量指标F按式（13）计算。该指标取值范围为[0,1]：数值越小，符合度越好；等于0表示分割对象与参考对象完全一致；等于1则表示完全不一致。

图2 图像的像素四种区域划分Figure 2 Pixels of images divided into four regions

1.4 基于差分进化算法的多尺度图像分割参数选择方法

多尺度图像分割最优分割参数解的求解采用差分进化算法进行优化时，选择分割算法的尺度参数、光谱特征权重与紧凑度权重参数作为差分进化算法的问题求解空间，将分割算法、分割评价方法及差分进化算法进行有效集成，具体集成流程如图3所示。

图3 基于差分进化算法的多尺度图像分割参数选择流程Figure 3 Selection process of multiscale image segmentation parameters based on differential evolution algorithm

1.4.1 分割参数种群初始化与分割评价

基于DE算法的多尺度图像分割参数选择涉及到尺度、光谱权重、紧致度权重等3个参数的优化，其问题的求解空间为这三个参数设置的最小与最大值。根据设置的种群大小NP，采用式（6）进行分割参数种群的初始化。

根据初始化种群个体的分割参数，利用多尺度分割算法对每个个体进行分割，并利用差异度指数F对每个个体的分割结果进行评价。

1.4.2 算法控制参数

DE算法涉及种群大小NP、差分进化最大代数G、差分策略、缩放因子F、杂交概率CR、差异度终止阈值的5个控制参数。其中NP、F和CR为控制参数，其设置的数值会影响搜索最优分割尺度参数和收敛速度；最大代数G与差异度终止阈值用于控制进化终止的条件，如果满足条件则终止进化，将得到最佳个体的分割参数作为最优分割参数输出；若否，继续差分进化。

种群大小NP：较大的群体会增加个体的多样性，加大搜索到最优解的可能性，但会降低收敛速度；较小的群体会加快收敛速度，但容易导致局部收敛或停止进化。

缩放因子F：用于控制搜索步长，较小的F会加快收敛，但容易导致局部收敛，出现“早熟”现象；较大的F值会增加算法跳出局部最优解的可能性，但F＞1会降低收敛速度，根据Storn和Prince的建议F的合理取值在[0.4，1.0]范围内[7]，较好的初始值 F=0.5[12]。

杂交概率CR：该参数的设置主要取决于所求解的问题，对于自变量相互独立的问题，CR可设置较小的值，而对于自变量相互依赖的问题，CR应设置较大一些。赵艳丽[9]指出，一般初始取值为0.3。

差分进化策略：依据变异和杂交算子的不同，可设计不同的差分进化策略。按“DE/a/b/c”来表示不同的差分策略。其中DE表示差分进化算法；a表示基向量的选择方式 （用rand表示随机选择；best表示选择当代种群中最佳个体）；b表示差分向量的个数，一般为1或2；c表示不同的杂交算子，分别用bin和exp表示二项式杂交和指数杂交。表1为常见的一些组合策略[6]。

表1 差分策略Table 1 Differential strategy

2 原型系统设计与实验

2.1 原型系统设计

根据设计的基于DE算法的多尺度图像分割参数选择模型，在Matlab中进行原型系统的设计。软件原型系统的图形用户界面如图4所示，左侧提供打开分割图像与参考对象、设置多尺度图像分割参数搜索空间与差分进化算法控制参数等用户交互接口，右侧提供图像显示，用于显示打开图像、参考对象及分割结果等数据。其中为了降低使用的复杂度，原型系统中将缩放因子F固定为0.5、杂交概率CR固定为0.3。

在利用该原型系统进行多尺度分割参数选择时，用户需要打开待分割图像及分割图斑的参考对象。设置完多尺度图像分割参数搜索空间与差分进化算法控制参数及输出结果的名称后，单击运行即可进行基于DE算法的多尺度图像分割参数选择，得到最佳的分割参数及其对应的分割结果。

图4 软件原型系统界面Figure 4 Software prototype system interface

2.2 实验数据

为了试验测试所使用的方法在图像分割参数选择的可行性，以2014年11月16日拍摄的福建省永安市燕西街道大炼村地区的部分航空彩色图像（如图5）为待分割图像进行试验。该航空图像的大小为512×512像素、以空间分辨率为0.6 m，包含位深为8比特的红、绿、蓝三个波段（通道）。该图像主要由耕地、房屋、道路和河流等主要地物构成，通过在ArcMap软件以该航空图像为底图，进行人工数字化，获得20块耕地地块作为参考对象（如图6所示）。

图5 待分割航空图像Figure 5 Aviation images to be split

图6 参考对象Figure 6 Reference objects

2.3 实验设计

2.3.1 试验的计算机环境

试验的原型系统软件在64位版本的Win10操作系统的笔记本上运行。笔记本的CPU为Intel（R）Core（TM）i3-2310M 四核 CPU（2.10GHz）、内存 10.0GB、显存2GB的NVIDIA GeForce GT 550M显卡。

2.3.2 试验的控制参数设计

通过将分割参数的搜索空间设置为：尺度参数[10,100]、光谱权重[0.6,0.9]、紧致度权重[0.4,0.6]；将差分进化算法的参数设置为：种群数量10、进化代数10、最小误差 1×10-16，差分策略选择为 DE/best/1/exp。利用软件原型系统进行尺度、光谱权重与紧致度权重参数的选择实验。

同时，为了评价差分进化算法选择的分割参数的稳定性，设计进行20次的最佳分割参数搜索选择实验，根据得到的实验结果进行算法的稳定性评价。

3 结果与分析

3.1 实验结果

对20次实验得到的的最佳分割参数按符合度从小到大排序，如表2所示。符合度最佳的分割结果如图7所示，符合度最差的分割结果如图8所示。

图7 符合度最小分割结果（实验12）Figure 7 Minimum compliance results（experiment 12）

图8 符合度最大分割结果（实验7）Figure 8 Maximum compliance segmentation results（experiment 7）

表2 多尺度图像分割参数差分进化选择结果Table 2 Differential evolution selection of multiscale image segmentation parameters

3.2 分析与讨论

针对本实验数据，从20次的实验结果看，差分进化算法在度尺度图像分割参数选择时，相同的参数搜索空间范围、相同的差分进化控制参数，得到的符合度值在[0.084,0.274]之间，均值为0.194，难以获得统一的最优分割结果，但都可以获得相对较理想的分割结果。从20次实验获得的分割参数的尺度值介于[31,55]、光谱权重和紧致度权重的取值介于参数设置的搜索空间范围之间，可以看出：不同的尺度参数、光谱和紧致度权重的组合，可以获得相近的分割结果。从实验数据的分析可以初步得出，多尺度图像分割对于相同的分割结果，可以由不同的参数组合进行分割得到。

4 结论

本研究实现了基于差分进化方法的多尺度图像分割参数的选择，可根据参考图与差异度准则选择“最优”的分割参数，相对于传统的人工试错的办法选择分割参数，减少分割参数选择的盲目性，达到了多尺度图像分割参数的客观、定量化选择的目标。

对于实验的航空彩色图像的“最优”的分割参数选择结果看，采用多尺度图像分割方法对其进行图像对象分割时，通过不同的尺度参数、光谱和紧致度权重的组合，可以获得相近的分割结果。因此，鉴于分割参数的组合数量之多，仅通过人工试错的方法，难以找到合适的分割参数。通过本文提出的方法可以获得较理想的分割参数及分割结果。