端部效应对长初级双边直线感应电机影响研究*

刘希军，魏 麟，朱新宇，高丽霞(中国民用航空飞行学院 航空工程学院，四川 广汉 618307)

0 引言

直线感应电机气隙的磁场是电机工作性能和设计的重要考虑依据，直线感应电机的能量转换主要通过气隙中的磁场得以实现。直线感应电机的气隙是开断的不连续的直线型气隙，行波磁场由入端向出端方向移动，由于直线感应电机的结构不连续性，使得气隙中即存在正常的行波磁场以外，亦存在附加磁场[1]。附加磁场会对直线感应电机的气隙磁场和工作性能产生影响，称为端部效应。

根据入端和出端对直线感应电机磁场和性能的影响，可对端部效应进行分类。由于初级电流固有的不平衡产生的影响称为第一类纵向端部效应；纵向端面磁通产生的影响称为第二类纵向端部效应；次级电流和次级板对气隙磁场产生的影响称为第一类横向端部效应和第二类横向端部效应[2]。

目前电磁加速驱动用直线感应电机多为极矩固定，通过控制线圈绕组频率控制电磁推力输出，采用闭环反馈控制方式，不断检测速度或者加速位移量[3]。然而，由于加速时间短、控制难度较大，再加上随着速度的不断增大，电机所需电流频率不断增加，逆变器频率必然要受到限制。

已有文献对普通型直线感应电机端部效应影响已有分析，但尚未有文献提出变极矩直线感应电机，以及极矩变化对端部效应影响进行分析。极矩的变化必然会对端部效应产生影响，需要分别采用场理论和路理论两种分析方法对电机的端部效应进行分析研究。

本研究提出一种极矩变化型的变极矩直线感应电机，恒定电流频率，通过改变电机极矩值控制电磁推力输出。

1 场理论分析端部效应参数方程

由于直线感应电机存在端部效应，可利用麦克斯韦方程组求解气隙磁场解析解，求解气隙磁场磁密表达式[4]。利用磁通密度的连续性可以对气隙磁场密度表达式中的复数常量C1，C2进行求解。长初级双边直线感应电机气隙磁通密度由正向基本行波、正向入端行波以及反向出端行波3部分组成[5]，即：

Bδ=Bδ0+Bδ1+Bδ2=Bδmej(ωt-βx+δm)+

(1)

端部效应参数m1，m2，m3分别为：

(2)

(3)

(4)

其中，系数k1，k2分别为：

k1=Gβ(1-s)

(5)

(6)

式中：s—滑差率；G—品质因数。

滑差率s为：

(7)

式中：vs—初级电流层沿x轴移动速度；vx—次级沿x轴移动速度。

品质因数G为：

(8)

式中：μ0—空气磁导率；σs—次级表面电导率，σs=2dσ；σ—次级电导率；2d—次级厚度；ω—电流角频率，ω=2πf；δe—电机电磁计算气隙，δe=kδkμδ0；kδ—电机气隙系数；kμ—电机饱和系数；δ0—电机初级铁心表面之间的距离；β—每极距长度对应电角度，β=π/τ；τ—电机极距。

2 路理论分析端部效应参数方程

对于直线感应电机而言，采用电磁场理论分析求解气隙磁场解析式，计算电机特性时，需考虑横向端部效应和纵向端部效应给电机带来的影响和损耗，这种计算方式多适用于初级电流已知的情况下[6]。若采用电压源供电的恒压驱动，则常采用计算电机等值电路的方式，分析直线感应电机在电压源供电情况下的性能。

对于长初级双边直线感应电机而言，为简化其分析，通常将直线电机分成两个部分，初级覆盖次级部分，与次级相互作用的部分称为有效部分，实现电机能量转化[7]。其余初级未覆盖次级部分称为无效部分，对电机能量转换无任何作用。有效部分和无效部分初级绕组串联，无效部分绕组对直线电机性能的影响用漏电抗在双边直线感应电机等效电路里体现。

长初级双边直线感应电机等效电路如图1所示。

长初级双边直线感应电机有效部分通常由次级长度决定[8-9]，无效部分绕组将产生较大漏抗降低电压值，使直线电机的效率和功率因数降低。为了减小能量损耗，通常采用初级绕组分段供电方式。

从电机等效电路图中可以看出，初级绕组串联电机的总阻抗为有效部分和无效部分之和，总漏抗亦为有效部分和无效部分之和[10]。初级漏抗xm和铁心损耗rt并联于电路中。忽略初级铁心损耗(rt≈∞)，忽略非磁性次级漏抗(x2≈0)。

根据等值电路理论可以对电路中各参量计算，求得端部效应参数表达式。次级电阻纵向动态端部效应系数、励磁电抗纵向动态端部效应系数为：

(9)

(10)

其中，系数K1，K2的值分别为：

K1=2pτcosθ1-K3[e-2pτsin(θ1-θ2+2pτ)+

e-2pτcos(θ1-θ2+2pτ)-sin(θ1-θ2)-

cos(θ1-θ2)]

(11)

K2=2pτcosθ1-K3[-e-2pτcos(θ1-θ2+2pτ)+

e-2pτsin(θ1-θ2+2pτ)-sin(θ1-θ2)+

cos(θ1-θ2)]

(12)

其中，θ1、θ2以及系数K3的值分别为：

(13)

(14)

(15)

采用场路复功率相等的原理计算横向端部效应系数Cr(s)，Cx(s)分别为：

(16)

(17)

其中，复量系数T为：

(18)

系数γ1，γ2，γ3分别为：

(19)

(20)

(21)

式中：a—初级铁心宽度的一半；c—次级铝板宽度的一半。

当滑差率s取值较小时，横向端部效应系数Cr(s)，Cx(s)可简化为：

(22)

Cx(s)=1

(23)

3 端部效应对电机气隙磁场影响

长初级双边直线感应电机的入端衰减参数m1的取值大小与电机次级厚度、次级电导率等设计参量，及供电频率、次级运行速度等因素相关。本研究改变某个设计参量，并保证其他参量不变的情况下，分析不同运行速度下，该参量对入端衰减参数m1的影响。

不同供电频率、气隙长度、次级厚度及次级电导率的情况下，入端衰减参数随运行速度的变化关系曲线，如图2所示。

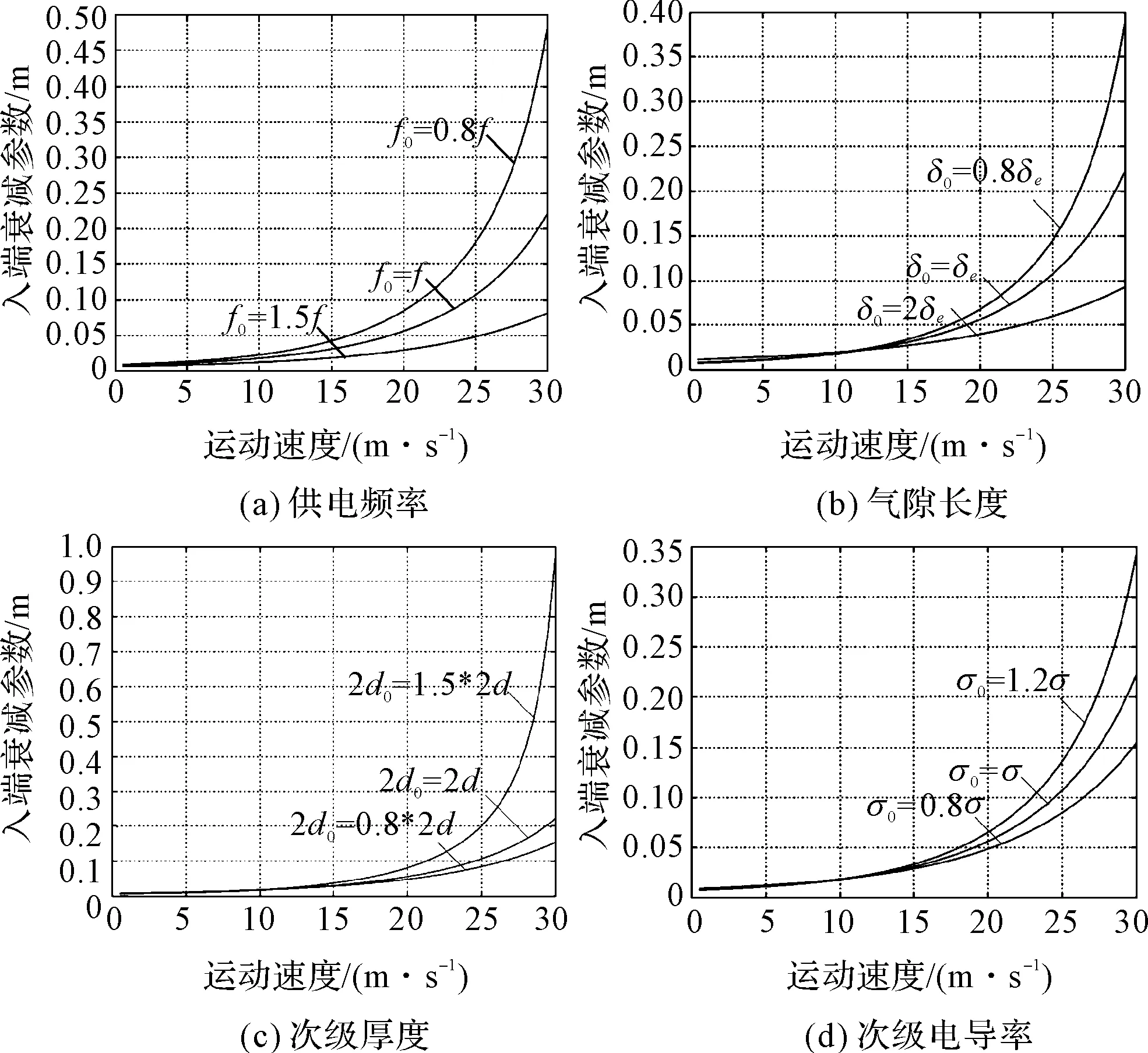
图2 m1在不同设计参量下随运行速度变化曲线

从不同的情况分析，随着运行速度的增加，入端衰减系数均增加，即随着速度的增大入端行波衰减速度减慢，对合成磁场影响增大。速度较小时，4种情况的入端衰减系数均较小，即低速时，入端行波磁场快速衰减，对磁场影响不大。

从图中分析可知，随着供电频率和等效气隙的增加，入端衰减系数m1减小；而随着次级厚度和次级电导率的增加，入端衰减系数m1增大。因而为了减小入端行波磁场对合成磁场的影响，应在保证电机性能不受影响的基础上，适当地增加供电频率和等效气隙，减小次级厚度和次级电导率，以降低入端行波磁场影响。

不同供电频率、气隙长度、次级厚度及次级电导率的情况下，出端衰减参数随运行速度的变化关系曲线，分别如图3所示。

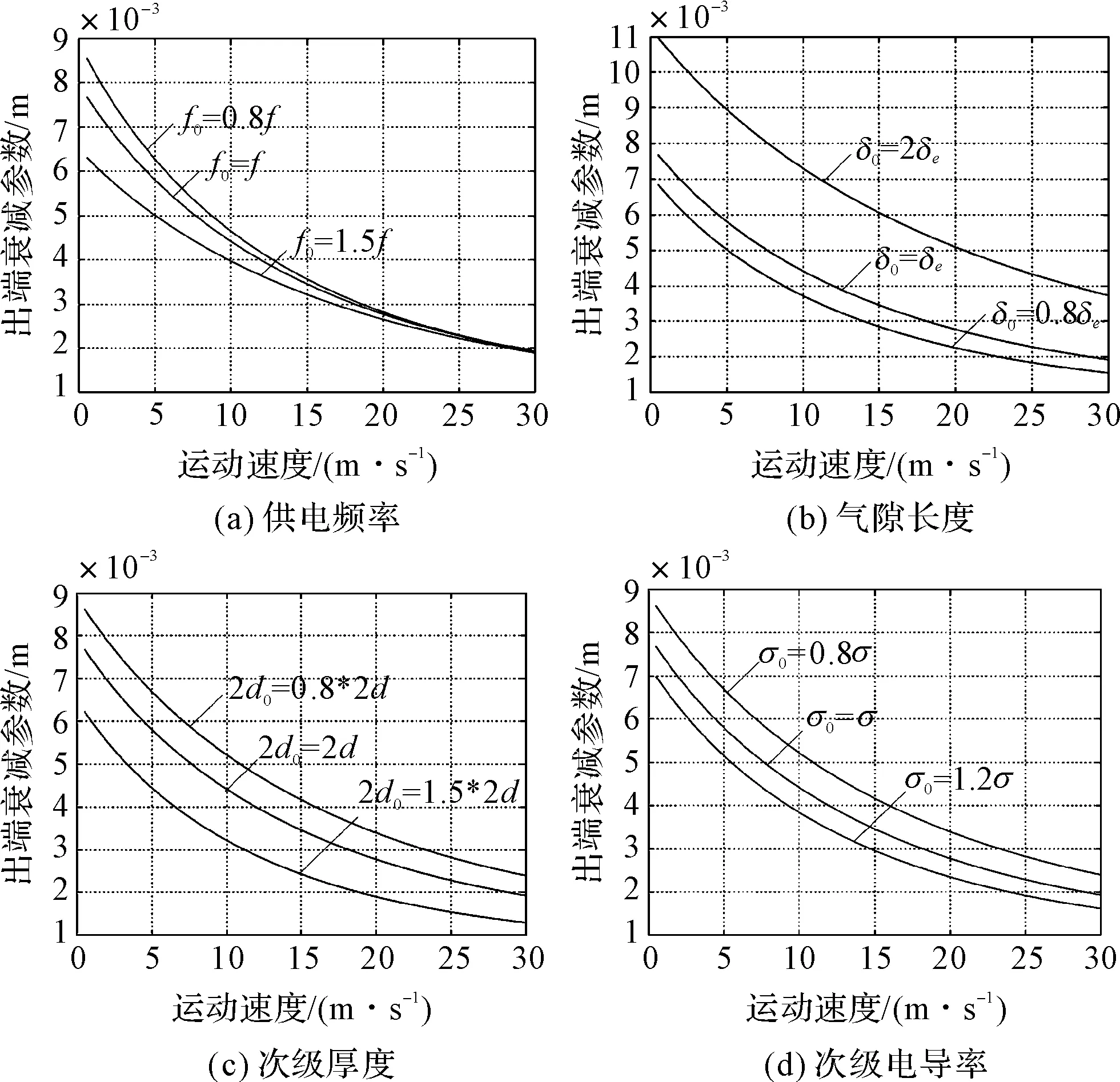
图3 m2在不同设计参量下随运行速度变化曲线

从各种情况分析均可发现，出端衰减系数决定的出端行波磁场对合成磁场的影响较小，且均随着运行速度的增大，出端衰减系数m2减小，即速度越大，出端衰减磁场衰减越快，对气隙磁场的影响就越小。随着供电频率、次级厚度和次级电导率的增加，出端衰减系数m2减小，而随着等效气隙的增加，出端衰减系数m2增大。

不同供电频率、气隙长度、次级厚度及次级电导率的情况下，端部效应行波波长随运行速度的变化关系曲线，如图4所示。

图4 m3在不同设计参量下随运行速度变化曲线

从图4中分析可知，端部效应的行波波长参数，随着运行速度的增加均增加。随着供电频率、等效气隙和次级电导率增加，端部效应行波波长m3减小，而随着次级的厚度的增加，端部效应行波波长m3增大，且在高速运行时，各设计参数对端部效应行波波长的影响近似相同。对于极矩变化型直线感应电机，极矩变化必然会对端部效应系数产生影响，进而影响电机磁场。

不同电机极距情况下，入端衰减参数、出端衰减参数，变化关系曲线，以及行波半波长和行波波速随电机极距变化的关系曲线，如图5所示。

图5 极矩变化对衰减参数影响

从图5中分析可知，由于变极距直线电机在设计时，从起始位置到加速完成位置，随着速度的增大，电机极距不断增加，可以发现，入端衰减参数、端部效应行波波长参数，随着运行速度的增加均增大，出端衰减参数随着运行速度的增加而减小。

入端衰减参数随极距的增加近似成指数规律增大，极距较小时，入端衰减参数数值非常小，入端行波衰减较快，仅仅在入端很短距离内存在，而在速度较大对应的极距较大区域内，入端行波衰减缓慢，对合成磁场有较大的影响。

出端衰减参数随极距的增加近似成指数规律减小，速度越大，极距越大，出端衰减参数越小，且参数值在整个过程中均较小，出端行波衰减极快，气隙磁场和电机性能影响较小，可忽略不计。

行波半波长和行波波速随电机极距的增大呈线性关系增大，低速时，行波波速小于同步速度，但随着速度的不断增大，其值不断趋于同步速度。

4 极矩变化对端部效应系数影响

通过长初级双边直线感应电机等值电路可知，其端部效应的影响通过端部效应系数修正，端部效应对变极距直线电机的影响即可通过端部效应系数体现。

励磁电抗纵向端部效应修正系数Kx(s)，次级电阻纵向端部效应系数Kr(s)随速度的变化关系，分别如图(6，7)所示。

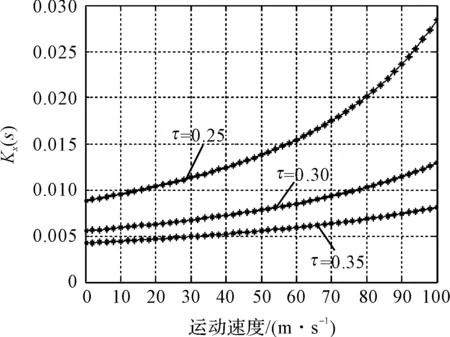
图6 Kx(s)随速度变化关系

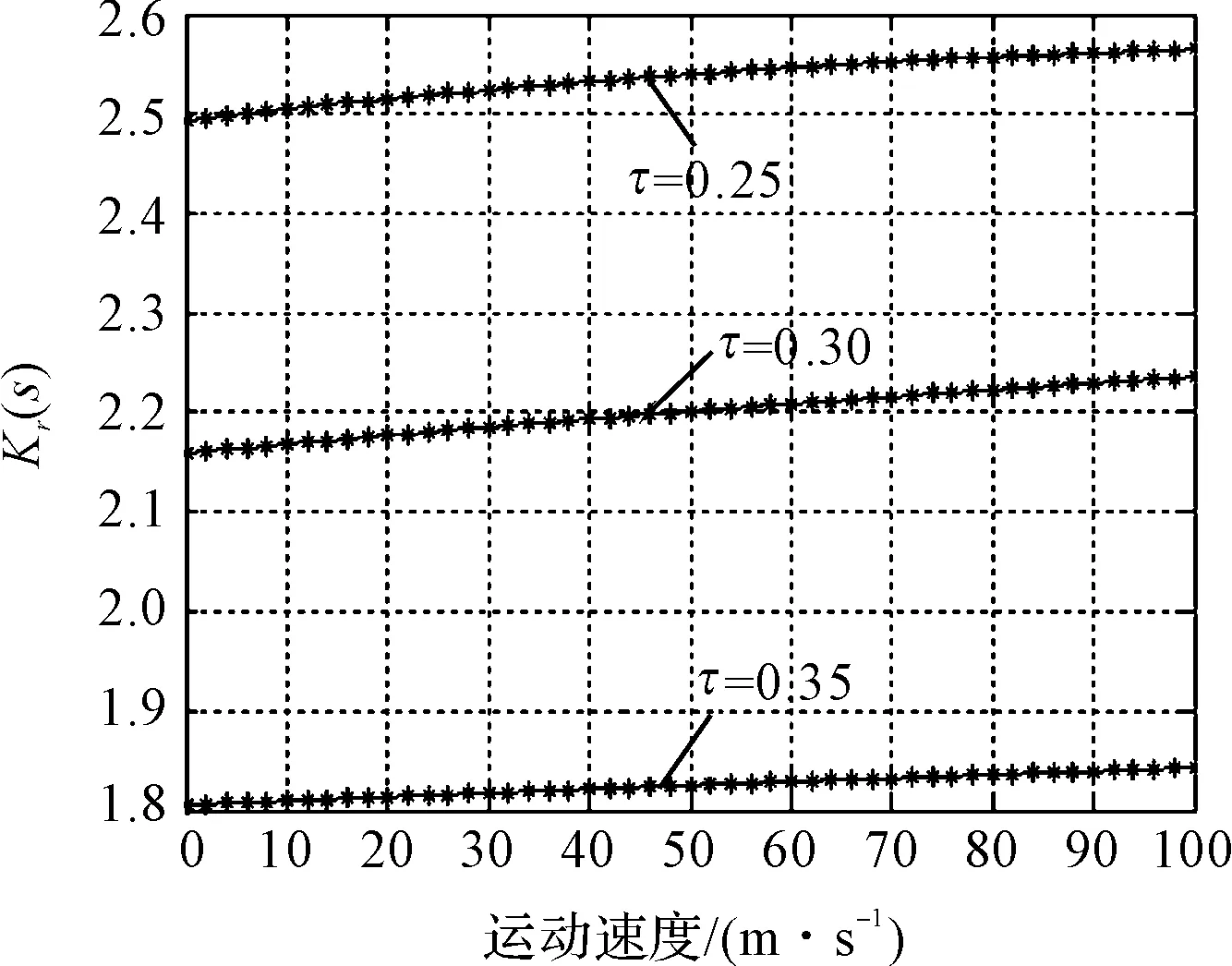
图7 Kr(s)随速度变化关系

分析可知，在整个加速过程中，Kx(s)和Kr(s)随速度的变化影响不大，均趋于恒定值。励磁电抗纵向端部效应修正系数Kx(s)取值较小，极距变化对其的影响不明显。次级电阻纵向端部效应系数Kr(s)值大于1，即修正后的次级电阻值大于未考虑端部效应影响时的值，即考虑纵向端部效应时次级损耗增加。

不同极距值对Kr(s)的影响亦很明显，极距越小，Kr(s)取值越大，对于极距变化型的直线电机而言，在整个加速过程中，电机极距是不断增大的，因而低速时纵向端部效应对电机的影响较大，高速时纵向端部效应影响将减小。

励磁电抗横向端部效应修正系数Cx(s)，次级电阻横向端部效应系数Cr(s)所对应的横向端部效应相对于纵向端部效应而言影响较小，Cx(s)和Cr(s)的值在整个加速过程中均趋于1。

5 结束语

本研究主要通过电磁场理论分析方法和路理论分析方法分别仿真分析了不同参量对端部效应的影响，以及极矩变化型直线感应电机极矩的变化对端部效应的影响。

仿真研究结果表明：电磁加速用直线感应电机在高速运行时，入端衰减系数呈指数倍增大，入端行波磁场衰减缓慢，出端衰减系数决定的出端行波磁场对合成磁场的影响较小；对于极矩变化型直线感应电机，电机极距越小，纵向端部效应影响越明显，随着速度的增加，极矩设计逐渐增大，因而在低速运行时，纵向端部效应对极矩变化型直线感应电机的影响更为明显，而横向端部效应受极矩变化较纵向端部效应而言不明显，因而在变极矩直线感应电机分析研究中暂可忽略。

[1] 鲁军勇,马伟明,李朗如.高速长初级直线感应电动机纵向边端效应研究[J].中国电机工程学报，2008,28(30)：73-78.

[2] KIM D, KWON B. A novel equivalent circuit model of linear induction motor based on finate element analysis and its coupling with external circuits[J].IEEETransactionsonMagnetics,2006,42(10)：3407-3409.

[3] 鲁军勇,马伟明,孙兆龙,等.多段初级直线感应电机静态纵向边端效应研究[J].中国电机工程学报,2009,29(33)：95-101.

[4] BAZGHALEH A Z, NAGHASHAN M R, MESHKATODDINI M R. Optimum design of single-sided linear induction motors for improved motor performance[J].IEEETransactionsonMagnetics,2010,46(11)：3939-3947.

[5] 鲁军勇,马伟明,许 金.高速长定子直线感应电动机的建模与仿真[J].中国电机工程学报,2008,28(27)：89-94.

[6] 王江波,李耀华,严陆光.长初级双边直线电机高性能控制策略[J].电工技术学报,2011,26(5)：126-131.

[7] 邓江明,陈特放,唐建湘,等.单边直线感应电机动态最大推力输出的滑差频率优化控制[J].中国电机工程学报,2013,33(12)：123-130.

[8] 许 金,马伟明,鲁军勇.无槽双边长定子直线异步电动机二维磁场分布及电磁力计算[J].电工技术学报,2008,23(9)：38-44.

[9] 胡维庆.步进电机细分驱动系统设计[J].轻工机械，2016，34(3)：57-60.

[10] KANG G, NAM K. Field-oriented control scheme for linear inductionmotor with the end effect[J].IEEEProceedings-ElectricalPowerApplications,2005,152(6)：1565-1572.