电动力绳系离轨系统电流与拉力混合展开控制

黄静，刘刚，朱东方，孙禄君

1.上海航天控制技术研究所，上海 201109 2.上海市空间智能控制技术重点实验室，上海 201109

自1957年第1颗人造卫星升空以来，航天器应用与人类社会的发展愈加紧密，但随着进入外层空间物体数量的不断增加，空间碎片环境问题也越发突出。为了适应空间探测的长期发展战略，世界航天大国都已开始关注新型空间应用技术。空间电动力绳系离轨系统是一种典型的空间碎片主动消除技术，该系统由在轨航天器、末端载荷及连接用的导电系绳构成，工作原理为利用绕地运行的导电缆绳切割地球磁场产生的动生电动势，此时在系绳两端分别安装电荷采集和发射装置即可有电流产生，与地磁场相互作用便产生了洛伦兹力，即电动力[1]。与其他方法相比，空间电动力绳具有能耗低、安全性高等优点，是处理中低轨道太空垃圾的有效手段[2]。在任意空间电动力绳任务中，都需要在发射至预定轨道后将系绳释放到预定长度。

由于电-力耦合、重力梯度、环境摄动等诸多因素存在，空间电动力绳系统是一类典型的非线性系统，在变化地磁场及电离环境下会呈现不稳定的动力学行为，需要在释放过程中对电动力绳系统的姿态进行控制[3]。目前，对于空间电动力绳系统动力学与控制技术正吸引着更多学者的密切关注，已产生了一些研究成果[4]。对于动力学建模，Somenzi等[5]研究了带有弹性的电动力绳系在振动和横向振动正则模态展开下的动力学稳定问题，对系统进行动力学分析，结果显示姿态不稳定来源于面外振动角和电动力的共振所产生的非零倾角。Zhong和Zhu[6]研究了长时离轨过程中采用裸线短系绳的电动力绳系统的动力学，考虑了由电动力引起的轨道摄动、大气阻力、地球扁率等影响。Li和Zhu[7]提出了电动力绳离轨过程中的珠点有限元模型，并应用辛算法处理离散有限元模型中能量和动量守恒问题，有限元法的缺点是计算量大，不易对动力学方程进行分析。潘伟等[8]采用在傅里叶空间描述的轨道动力学模型,将控制量电流表示为傅里叶级数的形式，并推导了用傅里叶系数作为参量的椭圆轨道运动的平均轨道根数方程。

对于电动力绳系统展开稳定控制问题，由于空间绳系展开控制系统不仅是非线性的、典型的欠驱动系统，还受到一些物理限制，比如拉力大小和电流强度都存在约束，这些给控制器的设计带来了困难。已有文献证明，通过拉力控制对于稳定空间绳系系统的面内运动是有效的。Rupp[9]首次尝试利用系绳长度及其变化速率稳定系绳轨道平面的天平动。近年来，Sun和Zhu[10]针对空间绳系系统展开控制问题设计了线性分数阶拉力控制律。由于以上文献并没有明确考虑非负的拉力限制，进一步研究的学者们考虑系统的各种限制，采用基于优化的方法，解决空间绳系的展开控制问题。例如，Steindl和Troger[11]在系绳拉力和长度变化速率的不等式约束条件下，针对空间绳系系统的面内展开控制问题设计了最优控制律。Wiliams[12]考虑了状态和控制约束，在不同的性能指标下设计了空间绳系面内展开与回收的开环最优控制律，并分别对有质量弹性系绳与刚性系绳分别进行建模与分析，说明了在控制律设计过程中，可以对弹性系绳进行简化，利用刚性系绳的展开回收控制律进行修正以对实际系统进行稳定控制。Wen等[13]考虑空间绳系系统面内展开控制问题，利用特殊的饱和函数处理拉力约束，提出了一种解析反馈控制律。

以上文献仅考虑了系绳二维面内展开的稳定控制问题，针对三维空间绳系展开控制，在调节拉力或长度进行控制基础上，还需要另外一种推进器与拉力进行混合控制，以稳定系绳的面外运动[14]。Kumar和Pradeep[15]利用拉力与面外推进器混合控制，设计了一种线性反馈控制策略在较短时间内稳定了空间绳系的三维运动。在电动力绳系统中，由于导电系绳与地磁场相互作用可以产生电动力，利用调节电流与拉力稳定电动力绳系统展开时的面内与面外运动可以充分发挥电动力绳系的优势，不额外增加化学推进装置，很大程度节约了燃料。Wen等[16]采用哑铃模型，忽略系绳质量，基于能量方法设计了近地圆轨道运行的三维电动力绳系统展开拉力与电流反馈控制律，并分析了不同轨道倾角下的控制效果，满足了控制要求，但控制律设计较为复杂。

本文主要考虑在近地椭圆轨道运行的三维电动力绳系统展开控制问题，仅通过调节系绳张力与电流，不依赖其他推进器，将导电系绳释放至期望长度并保持系统稳定。在已有的文献中，基本上都是忽略系绳质量，但是在实际系绳展开过程中，几千米的系绳存在一定质量，且对展开过程中的系统质心与等效质量有一定影响，如果忽略会降低控制精度。因此，本文考虑系绳展开过程中系统质心与等效质量变化的影响，建立二体电动力绳系卫星系统动力学模型。在控制方面，虽然已有文献对于考虑控制约束的电动力绳系统展开控制有一定研究，但基本上都是基于最优控制方法。虽然最优控制方法对于处理含约束的非线性控制问题非常有效，且能达到某些性能指标的最优，但是基于数值算法的最优化计算效率较低，不利于实际应用。因此，本文考虑系绳张力与电流存在约束的条件下，采用反步法结合抗饱和函数和辅助函数解决控制器受限问题，并引入动态尺度广义逆实现了对欠驱动系统的稳定控制。设计的姿态控制器保证了系统的稳定性，达到了控制要求，具有潜在的应用前景。

1 系统数学模型

1.1 电动力绳系卫星系统动力学模型

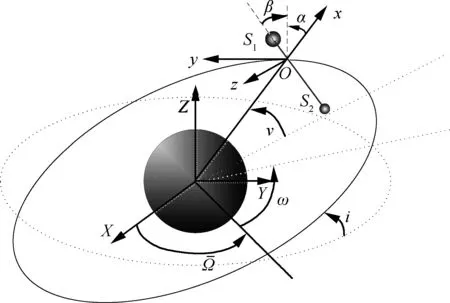
图1 电动力绳系卫星系统示意图Fig.1 Schematic of electro-dynamic tether satellite system

为简化分析过程，作如下假设：系绳为质量分布均匀的无弹性变形的刚性绳；系绳张力沿着绳的方向, 没有法线方向的能量耗散；系绳两端卫星视为质点，不考虑卫星本体的姿态。

采用欧拉-拉格朗日方法对系统建模，根据欧拉-拉格朗日方程

(1)

(2)

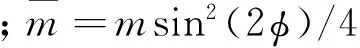
(3)

式中：md为释放出的系绳质量；ΛT=mT/m为系绳无量纲质量；Λd=md/m为释放出的系绳无维质量。经过推导，系统转动惯量Is为

(4)

因系绳释放过程中，系统的转动惯量随着绳长发生变化，经过计算，转动惯量随时间变化可以表示为

(5)

由于地球轨道半径R远大于系绳长度，且μeR-1=Ω2R2，μe为地球引力常数，则系统势能可以近似为

(6)

应用拉格朗日第二定理求得系统的动力学方程为

(7)

真近点角与地心半径的关系可以写为[17]

(8)

式中:e为轨道偏心率;p为轨道半通径。下面对Qα和Qβ进行计算，首先引入地磁场强度B=[Bx,By,Bz]T，由地球本体坐标系下国际地磁参考场2000模型描述，这里采用较为精确的偶极子模型[18]，描述为

(9)

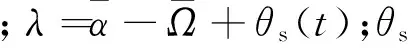
(10)

式中：

(11)

其中：I为系绳中的电流强度。为了方便计算，将方程进行无量纲，得到如式(12)～式(14)所示的动力学方程

(12)

(13)

(14)

式中:各导数为对无量纲时间τ的导数，d(·)/dt=Ωd(·)/dτ，ε=Ld/lc，lc为参考长度，设为系绳总长度。进一步定义

(15)

根据式(9)和式(10)，可以求得式(15)中各参数为

(16)

Cα=[(h1cosi+sinicos2β)sinλ-

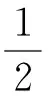
(17)

Cβ=[h2cosisinλ+(2cosusinα-

(18)

其中:

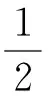
(19)

h2=2sinusinα+cosucosα

(20)

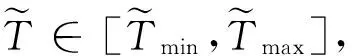
(21)

式中：

(22)

f(x1,x2)=

为了便于后面的控制器设计和稳定性分析，首先给出一个引理。

引理1[19]: 对于任意ε>0,a∈R，下面的不等式成立

(23)

式中:δ为常数，满足δ=e-(δ+1)，例如δ=0.278 5。

1.2 研究目标

将针对1.1节所示的动力学系统式(22)，考虑控制器输出限制

‖Q‖∞≤1

(24)

在干扰d存在的情况下，目标是通过合理的设计跟踪控制器，使x1、x2趋近于期望状态x1d、x2d。假设干扰d是有界的，即‖d‖∞≤dm，dm为估计的干扰上界。

2 控制器设计

2.1 抗饱和反步控制律设计

考虑到动力学系统具有级联形式，反步法具有设计过程简单、可调参数较少、所得控制器物理意义明显、可靠性好等优点，因此下面将采用反步法，并结合抗饱和函数和辅助函数解决控制受限问题。

首先定义跟踪误差

e1=x1-x1d

(25)

构造的Lyapunov函数为

(26)

将式(26)对时间求导，有

(27)

使闭环系统达到稳定的虚拟控制量αv选取为

αv=-ce1-ξ

(28)

式中：c>0为可调节的常数;ξ为防止控制输入饱和而设计的的补偿项，设计为[18]

(29)

其中:k2为正增益;ΔQ为实际控制输入与饱和值的差，具体形式见式(32)～式(34)。进一步定义

(30)

于是，通过式(25)和式(30)，可以得到误差动力学方程为

(31)

为了满足控制受限的条件式(24)，实际的控制输入Q为

Q=sat(Qs)

(32)

式中:Qs为期望的控制输入、饱和函数sat(·)定义为

(33)

这里Qm=1，将式(29)中的ΔQ定义为

ΔQ=Q-Qs

(34)

下面设计控制器Qs，构造增广的类Lyapunov函数

(35)

式中：b>0为可调节的常数，反映了速度偏差的权重。对函数V2求时间导数，并进行计算可得

(36)

由此可以看出饱和输入Q被动力学方程式(29)补偿，进一步设计Qs为

(37)

式中:g+(x1)∈R2×3表示控制系数矩阵g(x1)的广义逆(Moore-Penrose)，即

g+(x1)=

(38)

式中：k1>0，k2>0为正常数;N(e2)为抑制干扰所设计的函数，选取为

(39)

式中:ε>0为抑制干扰所设计的参数。将式(37)和式(39)代入式(36)，并根据引理1，则可以得到

(40)

于是可以推出

(41)

式中:kV=min(2c,2k1b)，ε1=δε，那么

(42)

可以看出，V2在可控范围内是非递增的，由Barbalat引理[20]推论可知，e1和e2为一致最终有界的，最终收敛到0附近一个小临域内。

(43)

其对时间的导数为

(44)

当k2>1/2，且ΔQ的模为有限值时，ξ可收敛并稳定在一个包含零点的区域S内，即

(45)

(46)

2.2 动态尺度广义逆引入

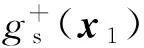
(47)

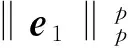
(48)

Q=sat(Qs)

(49)

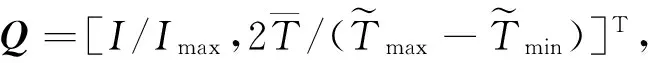
(50)

总结上面的控制器设计过程以及稳定性分析，可以得出以下定理。

本文提出的控制算法在实际应用中需要获取系绳面内角、系绳长度及相应的速度信息，可在两星上安装GPS、陀螺仪等测量卫星的姿态，通过光电编码器等测量系绳展开长度，利用“卷绕式”系绳释放机构，通过调节卷筒电机电压的脉冲宽度产生拉力(阻力)以控制系绳释放。并采用如空心阴极等离子接触器调节系绳中的电流，以满足控制的需要，使系统稳定。

3 数学仿真分析

本节在MATLAB/SIMULINK环境下进行数值仿真实验，验证本文所提出的控制算法的有效性。

在实际情况中，电动力绳系统在近地轨道附近受到的光压力、气动阻力等干扰力无量纲值幅值不超过0.01，因此，外部干扰上限设为dm=0.01。

根据约束条件及控制精度，经多次试验，控制参数选取为：c=1、b=5、k1=diag(5,5,0.3),k2=1。

仿真时间为无量纲时间τ=100，约为16个轨道周期。为了分析是否考虑系绳质量对仿真结果的影响，本节分为系绳质量为20 kg与0 kg两种情况进行仿真，仿真结果如图2～图8所示。

图2 系统等效质量随时间变化曲线Fig.2 Variation curves of system equivalent mass vs time

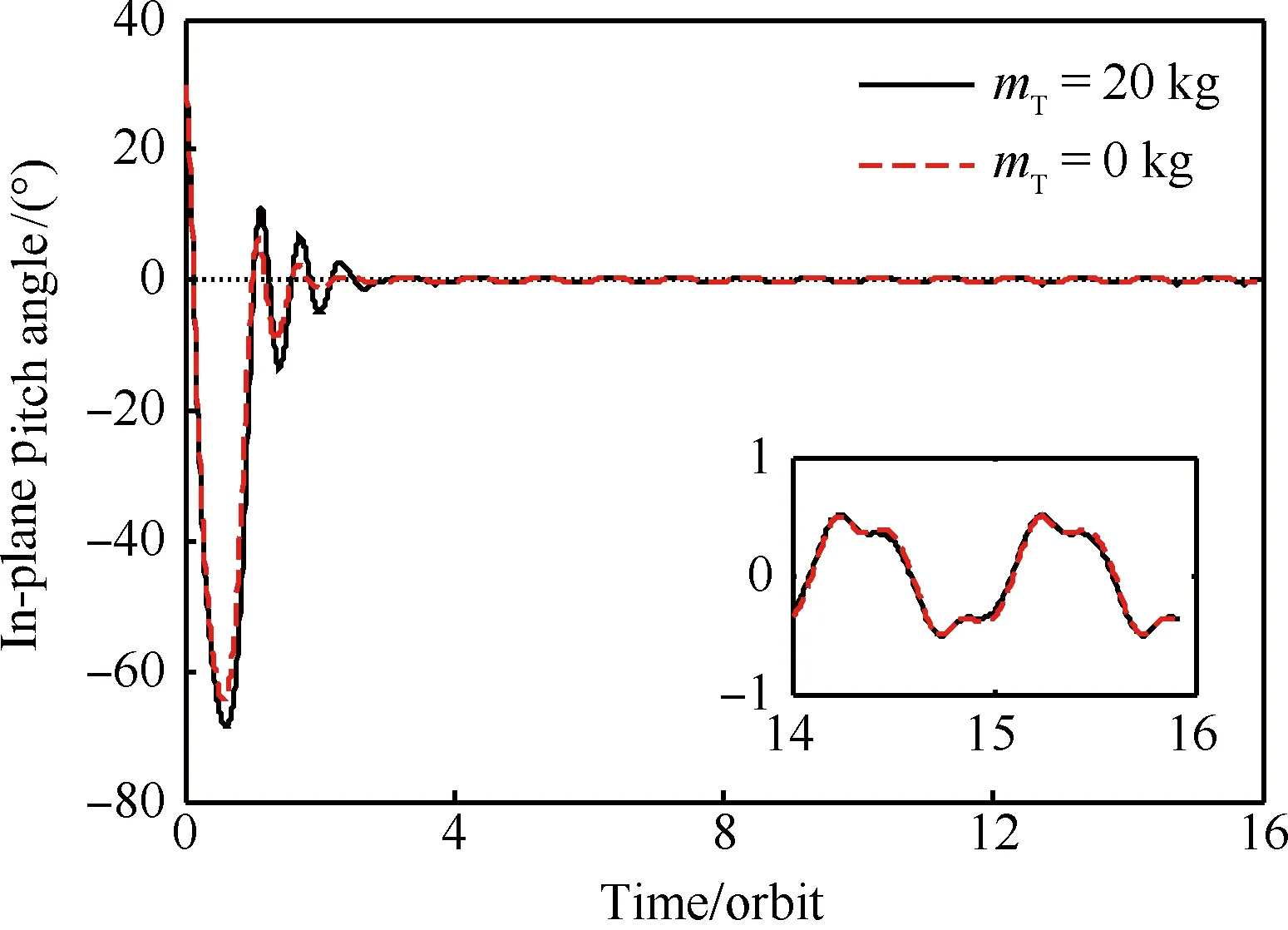
图3 面内俯仰角随时间变化曲线Fig.3 Variation curves of in-plane pitch angle vs time

图4 面外滚动角随时间变化曲线Fig.4 Viariation curves of out-plane roll angle vs time

图2为电动力绳系卫星系统等效质量随时间变化曲线，可以看出系绳质量对系统等效质量的影响比较大，不考虑系绳质量时系统等效质量稳定在29.126 2 kg，考虑系绳质量时系统等效质量随系绳长度产生变化。图3为面内俯仰角随时间变化曲线，可以看出在所提出的控制律作用下，面内角在2个轨道周期左右收敛到0°附近，最大摆动角约67°，在2个轨道周期后，面内角在0°附近摆动，由于动态尺度广义逆与广义逆存在一定误差，因此摆动角在执行机构未达到饱和的情况没有收敛到0°，摆动周期约为1个轨道周期，幅度为0.5°，满足在系绳展开过程中面内角稳定的要求。图4为面外滚动角随时间变化的曲线，从图4中可以看出，面外角振荡几次之后在2个轨道周期左右收敛到0°附近，在2个轨道周期后，面内角在0.2°附近摆动，摆动周期约为0.5个轨道周期，幅度为0.3°，满足在系绳展开过程中面外角稳定的要求。图5为系绳长度随时间变化曲线，可以看出，系绳长度从初始的50 m平稳地展开至5 000 m，2个周期后在拉力与电流的共同作用下维持在4 992 m附近，系绳最终长度误差在0.2%以内，满足控制精度的要求。

图5 系绳长度随时间变化曲线Fig.5 Variation curves of tether length vs time

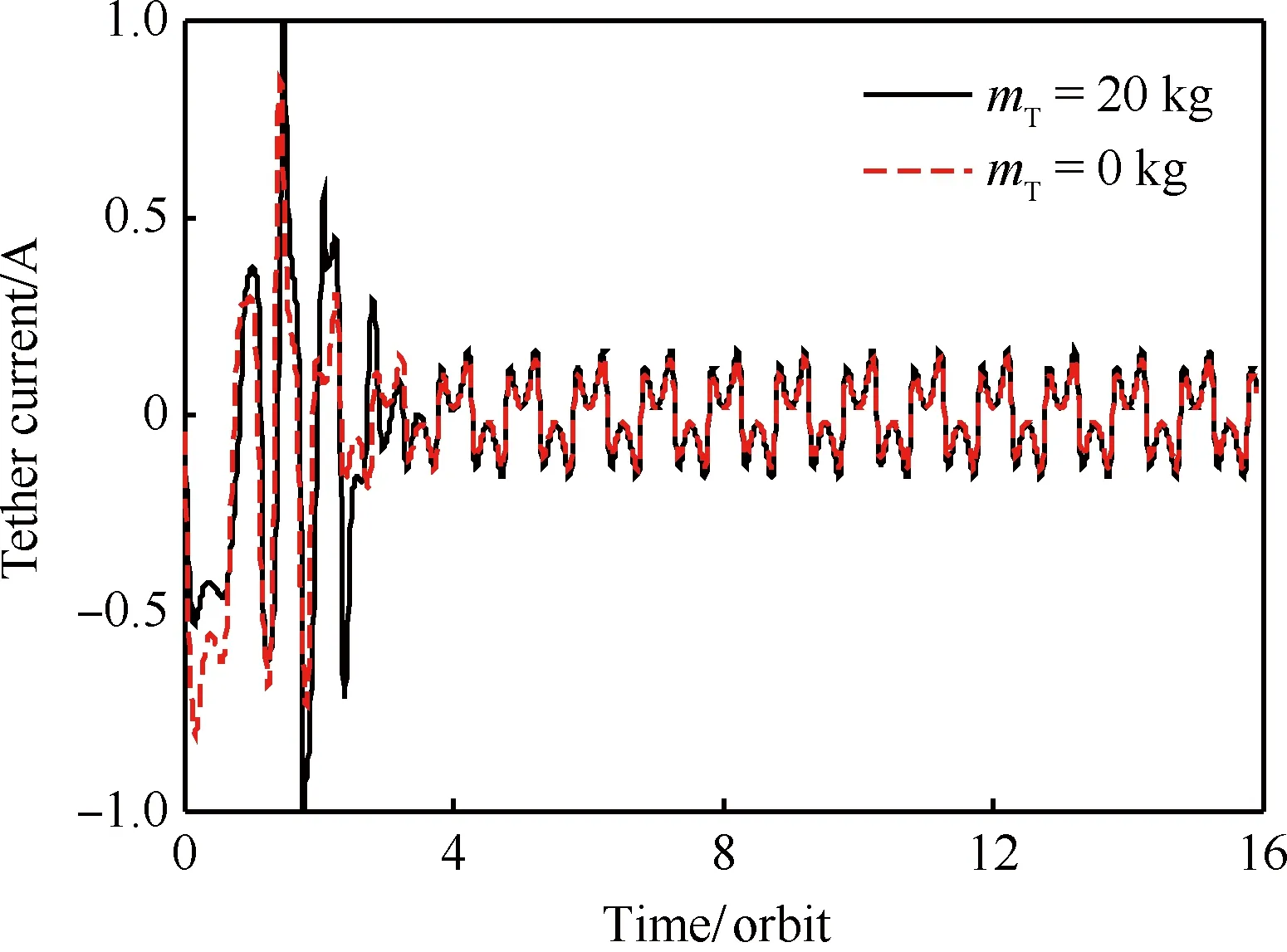
图6 系绳电流随时间变化曲线Fig.6 Variation curves of tether current vs time

图8和图9分别为两种情况下16个轨道周期和最后两个轨道周期内的系绳末端在以母星(火箭末级等)为坐标原点的轨道坐标系下的变化轨迹。可以看出，释放出的系绳末端在沿x方向释放到4 992 m左右，并在稳定后作小幅度周期性运动，表明是否考虑系绳质量对系绳末端的三维运动影响不大。说明了在系绳电流、拉力受限以及摄动影响的情况下，设计的欠驱动反步控制器能保证整个闭环电动力绳展开系统的一致最终有界稳定性，充分验证了本文所提出的非线性控制器的有效性。

图7 系绳拉力随时间变化曲线Fig.7 Variation curves of tether tension vs time

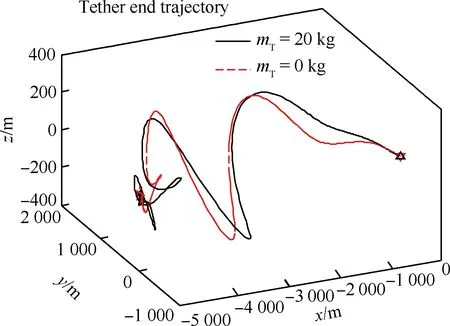
图8 系绳末端在轨道坐标系下变化轨迹Fig.8 Tether end trajectory in orbital coordinate frame

图9 系绳末端在轨道坐标系下变化轨迹 (最后两个轨道周期)Fig.9 Tether end trajectory in orbital coordinate frame (the last two orbit periods)

4 结 论

本文针对近地轨道电动力绳系统系绳展开控制问题，设计了一种仅通过调节系绳张力与电流的非线性欠驱动电动力系绳展开控制律。

1) 建立了考虑系绳质量的近地轨道二体电动力绳系卫星系统动力学模型，考虑了展开过程中系统质心与等效质量随展开系绳长度的影响，减小了数学模型与实际系统的建模误差。

2) 提出的控制算法仅通过调节系绳张力与电流，不依赖其它推进器，将导电系绳释放至期望长度并保持系统稳定。

3) 考虑系绳张力与电流存在约束的条件下，提出了一种基于反步法结合抗饱和函数和辅助函数的控制律，并引入动态尺度广义逆实现了对欠驱动系统的稳定控制。仿真结果表明，系绳长度释放至目标长度，误差保持在0.2%以内，同时，系绳姿态面内外角分别保持在小幅度摆动，设计的姿态控制器保证了系统的稳定性，达到了控制要求，具有潜在的应用前景。

4) 在今后的研究中，将在此基础上，进一步考虑系绳挠性的影响，设计更加具有工程意义的控制律。

[1] SHIAH A, HWANG K S, WU S T, et al. Three-dimensional simulation of current collection in space[J]. Planetary and Space Science, 1997, 45(4): 475-482.

[2] PARDINI C, HANADA T, KRISKO P H. Benefits and risks of using electrodynamic tethers to de-orbit spacecraft[J]. Acta Astronautica, 2009, 64(5): 571-588.

[3] HOYT R P. Stabilization of electrodynamic tethers[C]∥Proceedings of 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Reston, VA: AIAA, 2002: 1-8.

[4] 蔡洪, 杨育伟, 郭才发. 电动力绳系研究进展[J]. 宇航学报, 2014, 35(11): 1223-1232.

CAI H, YANG Y W, GUO C F. Review of electrodynamic tether system[J]. Journal of Astronautics, 2014, 35(11): 1223-1232 (in Chinese).

[5] SOMENZI L, IESS L, PELAEZ J. Linear stability analysis of electrodynamic tethers[J]. Journal of Guidance, Control, & Dynamics, 2012, 28(5): 843-849.

[6] ZHONG R, ZHU Z H. Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit[J]. Journal of Spacecraft & Rockets, 2015, 50(3): 691-700.

[7] LI G Q, ZHU Z H, Long-term dynamic modeling of tethered spacecraft using nodal position finite element method and symplectic integration[J]. Celestial Mechanics & Dynamical Astronomy, 2015, 123(4): 363-386.

[8] 潘伟, 路长厚, 李吉栋, 等. 基于傅里叶展开的电动力绳系卫星最优控制[J]. 航空学报, 2011, 32(9): 1714-1721.

PAN W, LU C H, LI J D, et al. Optimal control of electrodynamic tethered satellites based on Fourier series expansion[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1714-1721 (in Chinese).

[9] RUPP C C. A tether tension control law for tethered subsatellites deployed along local vertical: NASA-TM-X-64963[R]. Wahsington, D.C.: NASA, 1975, 1-28.

[10] SUN G H, ZHU Z H. Fractional-order tension control law for deployment of space tether system[J]. Journal of Guidance, Control, & Dynamics, 2014, 37(6): 2062-2066.

[11] STEINDL A, TROGER H. Optimal control of deployment of a tethered subsatellite[J]. Nonlinear Dynamics, 2003, 31(3): 257-274.

[12] WILLIAMS P. Optimal deployment/retrieval of tethered satellites[J]. Journal of Spacecraft & Rockets, 2008, 45(2): 324-343.

[13] WEN H, ZHU Z H, JIN D P, et al. Space tether deployment control with explicit tension constraint and saturation function[J]. Journal of Guidance, Control, & Dynamics, 2016, 39(4): 915-920.

[14] STEINDL A, Optimal control of the deployment (and retrieval) of a tethered satellite under small initial disturbances[J]. Meccanica, 2014, 49(8): 1879-1885.

[15] KUMAR K, PRADEEP S. Strategies for three dimensional deployment of tethered satellites[J]. Mechanics Research Communications, 1998, 25(5): 543-550.

[16] WEN H, JIN D, HU H. Three-dimensional deployment of electro-dynamic tether via tension and current control with constraints[J]. Acta Astronautica, 2016, 129: 253-259.

[17] VALLADO D A. Fundamental of astrodynamics and applications[M].New York: Microcosm Press, 2007: 103-117.

[18] WILLIAMS P. Libration control of electrodynamic tethers using predictive control with time-delayed feedback[J]. Journal of Guidance, Control, & Dynamics, 2015, 32(4): 1254-1268.

[19] POLYCARPOU M M, IOANNOU P A. A robust adaptive nonlinear control design[J], Automatica, 1996, 32(3): 423-427.

[20] SLOTINE J J E, LI W. Applied nonlinear control[M]. Beijing: China Machine Press, 2004: 121-155.

[21] 黄静, 李传江, 马广富, 等. 基于广义逆的欠驱动航天器姿态机动控制[J]. 自动化学报, 2013, 39(3): 285-292.

HUANG J, LI C J, MA G F, et al. Generalised inversion based maneuver attitude control for underactuated spacecraft[J]. Acta Automatica Sinica, 2013, 39(3): 285-292 (in Chinese).