基于HB-AFT算法的阵发性混沌振动研究新方法*

李磊 张智勇,† 芮筱亭 陈予恕

(1.南京理工大学 理学院, 南京 210094) (2.南京理工大学 发射动力学研究所, 南京 210094)(3.哈尔滨工业大学 航天学院, 哈尔滨 150001)

引言

随着科学技术的发展,混沌理论有了长足的发展. 阵发性混沌理论从20 世纪80 年代起步,在等离子体[1]、非线性电路[2]、流体力学[3]、细胞力学[4]和机器人动力学[5]等分析中取得了大量理论和实验成果,由此受到了广泛的关注.阵发性混沌的主要特征是规则和不规则运动伪随机交替出现.常见的阵发性混沌经过折叠分岔、亚临界Hopf分岔和亚临界倍周期分岔伴随系统全局结构的重整化产生,Pomeau和Manneville[6]把这三类阵发失稳嵌入混沌的方式分别定义为阵发Ⅰ、Ⅱ和Ⅲ型混沌,显然这三种分岔并不是阵发混沌产生的充分条件[7].近20年来,阵发性混沌理论得到了进一步丰富[8],阵发V型、X型混沌、开关(on-off)阵发、激变阵发等多种新的阵发混沌响应模式被理论和实验发现.阵发性混沌演化涉及系统全局动力学特性的转变,因此理论上研究困难,常采用数值方法进行计算分析.然而,阵发性混沌往往发生在失稳不动点附近,由于临界慢化现象[9]的发生,对数值积分模拟要求高精度和较长的计算时间.综上所述,就阵发性混沌研究而言,无论在理论发展、工程应用还是研究手段领域,都存在大量开放性问题,方兴未艾.

有许多经典的数值方法、定量方法和解析方法可对非线性动力系统的特性进行分析.一般把所求问题看成常微分方程的初值问题,采用数值积分方法来求解系统的渐近稳态响应[10],并采用Poincare截面、频谱图、Lyapunov指数和数值分岔图等分析系统的混沌特征.但是,由于阵发性混沌响应的陡变特性,在数值积分求解过程中需要频繁改变步长,且临界慢化现象使得接近失稳位置的稳态响应计算非常耗时[11].小参数摄动法、平均法、多尺度法等各种经典的定量方法受到小参数条件、可积条件、级数展开条件等的限制[12],而谐波平衡法对于复杂非线性系统谐波平衡本身就是极为困难的.另外,上述定量解析方法在高次谐波解求解时,由计算工作量原因,通常仅求解一次或二次谐波解,可是相关研究表明高次、小谐波分量的忽略可能会对系统的稳定性带来极大的误差甚至错误[13].

HB-AFT方法是Yamauchi[14]提出来的一种半解析半数值的隐式谐波平衡法.该方法在求解系统周期响应过程中把响应和非线性函数同时设为谐波解形式,根据系统的离散时频特性建立谐波系数之间的关系,对于复杂非线性项无需级数展开、积分处理等近似过程,因此该方法具有一定的普遍适用性[15]. 随后,Kim等[16]引入广义的DFT变换技术,使HB-AFT方法可自动求解系统的准周期解. 最近,Didier等[17]提出的随机HB-AFT方法能很好的用于包含随机强非线性的转子系统的非线性响应分析. Zhang等[18]将同伦延拓技术嵌入HB-AFT方法,结合Hsu求解Floquet单值矩阵的离散方法,给出了一整套追踪系统周期响应和稳定性分析的全频域快速方法.

Duffing振子系统已经成为分析非线性动力学行为的一种经典模型,而且在许多情况下可以使用不同形式的Duffing方程对一些工程非线性问题进行定性分析[19,20].Duffing系统是研究阵发性混沌振动的一种主要模型,阵发性混沌现象在各类型Duffing系统中被大量研究[21-23].简谐激励Duffing系统(1)式的阵发性混沌现象被广泛研究[11,24],不过缺少对其动态演化的相关分析.

(1)

鉴于以上背景,本研究从简谐激励Duffing系统阵发性混沌现象出发,基于非线性动力学理论,采用HB-AFT方法结合Floquet理论,对非线性动力系统的典型阵发性混沌行为的演化展开研究,拟提供一种阵发性混沌研究的新方法.

1 理论与方法

1.1 HB-AFT方法求解周期响应

不失一般性,求解响应周期为2π的解,对于非线性系统

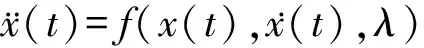
(2)

首先,进行响应和非线性函数谐波平衡化过程：

(3)

把等式(3)代入系统(2),各阶谐波平衡可得：

g(P,Q)=0

(4)

其中,P、Q分别表示响应和非线性力谐波系数.

把Q记为已知,可采用Newton-Raphson迭代求解不动点P,

J(i)(P(i+1)-P(i))+g(i)=0

(5)

其中,迭代Jacobian矩阵,

J=dg(P,Q)/dP

=∂g(P,Q)/∂P+∂g(P,Q)/∂Q·dQ/dP

(6)

迭代求解(5)式,只有(6)式中dQ/dP是未知的,下面通过AFT变换[22]给出该关系.

系统响应x(t)的时域离散信息可由反有限傅里叶变换(Inverse Discrete Fourier transform, IDFT)给出：

(7)

这里Pk=ak+ibk,n=0,…,N-1,x(n)为x(t)在第n个时间点的值,N为时间离散点数.

(8)

则Q可由有限傅里叶变换(Discrete Fourier transform, DFT)给出：

(9)

其中Qk=ck+idk,当n=0,φ为1, 否则φ等于2.

从(7)～(9)式可见,Qk是Pk的函数,因此可以求得dQ/dP的显式表达式.

1.2 嵌入弧长延拓的HB-AFT方法

以λ为控制参数,由(5)式迭代求解会在转向点失效[25],对此问题可用弧长延拓法把(4)式转化为：

(10)

在初始条件(P(s0),λ(s0))=(P,λ)0下的求解问题.式(10)中λ为系统参数变量,s为曲线(P(s),λ(s))的弧长变量,(P,λ)0为(10)式一个已知解.

常用牛顿迭代校正法[25]求解(10)式,具体求解过程为：

首先,由已知解(P,λ)0预估一个解

(11)

然后,对(P,λ)1进行Newton-Raphson迭代,

(12)

1.3 稳定性分析

对由HB-AFT方法求得的系统周期解,基于Floquet理论[7],由Hsu阶跃函数法求得系统Floquet单值矩阵[17].

(13)

对于(13)式系统,用ΔU扰动HB-AFT过程求得的T为周期的解U*(τ)如下：

d(U*(t)+ΔU)/dt=F(t,U*(t)+ΔU)

(14)

可得(14)式的线性化表达式

dΔU/dt=∂F(t,U*(t))/∂U(t)*·ΔU

=A(t,U*(t))ΔU

(15)

周期解U*(τ)的局部线性稳定性可通过Floquet理论,由周期变系数微分方程(15)式ΔU的稳定性来判断.由Hsu阶跃函数法,给出单值矩阵的计算公式：

(16)

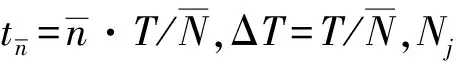
就周期解分岔特性而言,周期为T周期解稳定的条件为所有的Floquet乘子(即单值矩阵B的特征值λm)都位于复平面上的单位圆内,根据λm通过单位圆的方式可知周期解的失稳的三种基本形式[7]：

(1)λm在+1处越出单位圆,系统周期响应可能发生跨临界分岔、对称破缺分岔、折叠分岔；

(2)λm在-1处越出单位圆,则周期响应发生倍周期分岔；

(3)若两个共轭乘子离开单位圆,则周期响应发生二次Hopf分岔.

一般来说,若系统发生折叠分岔、亚临界Hopf分岔或亚临界倍周期分岔后,系统的原稳定周期吸引子并未发生转迁[24],伴随系统结构的重整化将分别发生阵发Ⅰ、Ⅱ和Ⅲ混沌现象[7].

2 算例

对于(1)式Duffing系统,选取文献[11,24]参数c=0.25,k=-1,α=1,ω=1进行分析.当激励幅值A=0时,对无阻尼未扰系统(1)式进行平衡点稳定性分析,可知系统具有两个中心(±1,0)和一个鞍点(0,0).

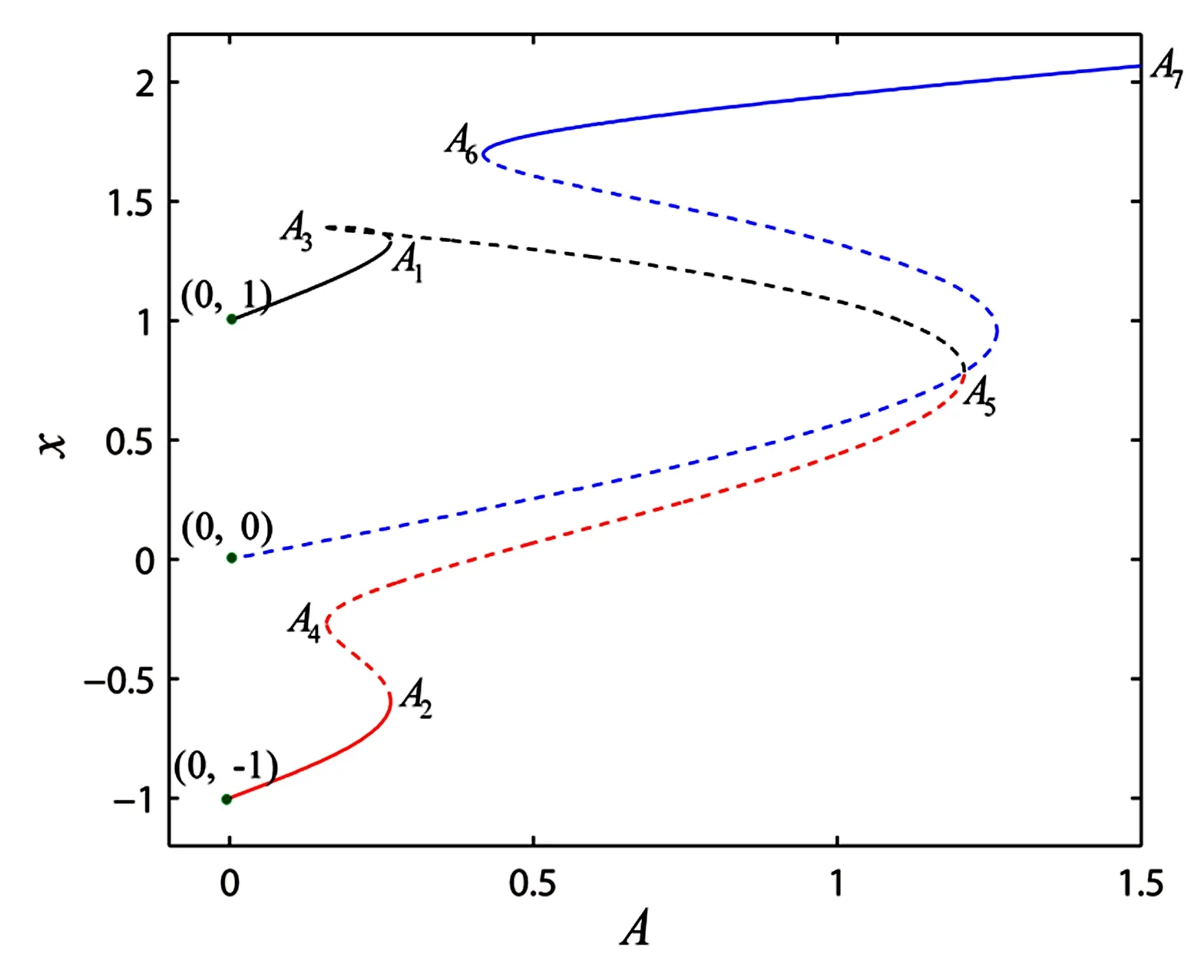
图1 全局周期1解分支Fig.1 The trajectory of global period-1 branch

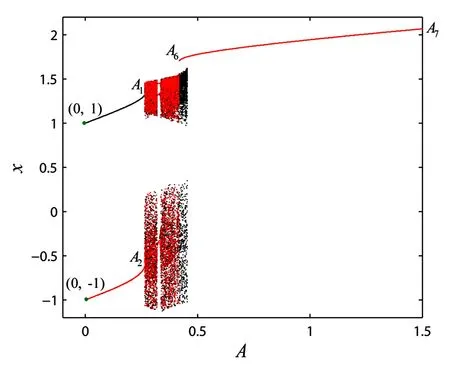
图2 数值分岔图,其中黑点、红点分别为随A向前、向后扫频的数值积分结果Fig.2 Numerical bifurcation diagram, the black and red dots denotes A sweeping up and down

以激励幅值A为控制参数(即式(10)中λ=A),取谐波次数K=10,式(12)迭代误差取10-15,采用嵌入弧长延拓的HB-AFT方法追踪系统的周期1解分支(相对激励周期而言).如图2所示,系统受扰后从平衡点出现三条周期解分支,与未扰系统类似,两中心产生的周期1分支是稳定的,鞍点受扰产生的周期1分支是不稳定的,这与文献[26]的解析分析结果一致.两条稳定的周期解在A1、A2点通过折叠分岔失稳,如表1、表2所示,周期1解分支的Floquet乘子在转向点穿过+1轴离开单位圆.随后,不稳定的周期1解分支在A3、A4通过折叠分岔产生半稳定[27]的周期解分支A3-A5、A4-A5.另一方面,从鞍点产生的周期解分支在A6经折叠分岔产生较大振幅的稳定周期轨线A6-A7.上述结果与数值分岔图是吻合的.随控制参数A的改变,如图3所示系统的全局周期解共存特性及其稳定性变化显著.

表1 周期1分支在转向点A1附近的Floquet乘子λmTable 1 Floquet multipliers λmof period-1 branch around the turning point A1

表2 周期1分支在转向点A2附近的Floquet乘子λmTable 2 Floquet multipliers λmof period-1 branch around the turning point A2

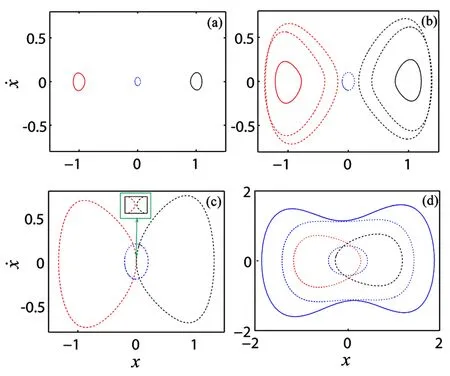
图3 系统在A激励幅值取(a) 0.1,(b) 0.2,(c) 0.4和(d) 0.8时的稳定(实线)、不稳定(虚线)周期1解共存特性Fig.3 Coexistence of stable (solid) and unstable (dotted) period-1 solutions, excitation amplitude A taken as (a) 0.1, (b) 0.2, (c) 0.4 and (d) 0.8

如表1、表2所示,随着控制参数A加大,两条稳定的周期解分支在AT=0.26497948248附近同时发生折叠分岔,这是由于系统的对称性导致的.如图4所示,系统折叠分岔失稳后系统的稳态响应并未发生危险分岔跳跃到其他吸引子上[24],且在临近不动点A1、A2位置经历逆切分岔(inverse tangent bifurcation)[8]缓慢通过,由此可以判断系统此时触发阵发Ⅰ型混沌振动模式,可以认为AT是此系统阵发Ⅰ型混沌的阈值.

图4 激励幅值A在0.16到0.32之间的全局周期1解分支和数值分岔图Fig.4 The trajectory of global period-1 branch and numerical bifurcation diagram for excitation amplitude A taken 0.16 to 0.32

如图5所示,随着控制参数越过阵发I型混沌阈值AT,系统的时域响应出现了规则与不规则伪随机交替.当A值继续增加,不规则运动所占区间增大,最后系统完全进入不规则运动,由图6 Poincare映射可见,系统响应在此过程中逐渐远离分岔不动点A1、A2(图6局部放大图a3和a4),这也是阵发Ⅰ型混沌与阵发Ⅱ型、Ⅲ型混沌不同特征之一[8].另外,系统存在稳定的周期1解与混沌解共存的状态,见图6(c).

图5 激励幅值A取(a) 0.26498,(b) 0.26499,(c) 0.26501和(d) 0.27000时的时间历程Fig.5 Time series for excitation amplitude A taking (a) 0.26498,(b) 0.26499,(c) 0.26501 and (d) 0.27000

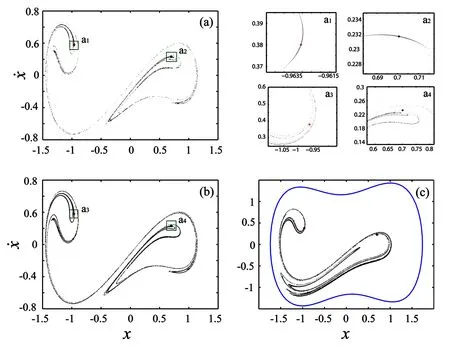
图6 激励幅值A取(a) 0.26498,(b) 0.27000和(c) 0.45000时的Poincare映射,其中蓝线为相轨线Fig.6 Poincare maps for excitation amplitude A taking (a) 0.26498,(b) 0.27000 and (c) 0.45000, where the blue line is phase trajectory

3 结论

以Duffing系统为研究对象,对经典的单频激励Duffing系统的分岔特性进行了深入研究.发现该系统包含丰富的周期解分支共存和失稳特性,且在一定条件下存在阵发I型混沌行为,具有一定的基础理论价值.阵发性混沌演化由于涉及系统全局动力学特性的转变,理论上分析困难.本研究针对该问题,从非线性动力学角度出发,采用嵌入弧长延拓的HB-AFT方法结合Floquet理论,提供了一套阵发性混沌演化的研究方法.本文方法本质上属于频域方法,可以快速而精确地自动追踪系统周期解分支并判断其稳定性.通过系统全局周期解特性的分析,能够对系统经典阵发类型的演化进行全局分析.