求解大规模多背包问题的高级人工鱼群算法

李 迎, 张 璟, 刘 庆, 张 伟

(1. 西安理工大学自动化与信息工程学院, 陕西 西安 710048; 2. 西安理工大学计算机科学与工程学院, 陕西 西安 710048; 3. 北京天云融创软件技术有限公司, 陕西 西安 710075)

0 引 言

多背包问题(multiple knapsack problem,MKP)是一个很经典的NP-Hard组合优化问题[1-2],它可以作为很多实际问题的模型,例如多资源调度、交通规划、资本预算、材料切割等[3-4]。

目前求解多背包问题的算法主要分为两大类,第一类是传统的搜索算法,例如精确求解法、启发式算法、元启发式算法等[5-6],均取得了一些成效,但是随着实际应用中问题规模的不断扩大,严苛的约束和指数级增长的解空间使得常规算法很难得到最优解。另一类是基于群智能的进化算法,例如遗传算法(genetic algorithm,GA)[7]、粒子群优化(particle swarm optimization,PSO)算法[8]、蚁群优化(ant colony optimization,ACO)算法[9]和人工鱼群算法(artificial fish swarm algorithm,AFSA)等,它们由于实现简单、鲁棒性强等优点被越来越广泛的应用[10-16]。其中,GA是基于个体竞争的寻优机制,在染色体进化和淘汰的过程中,种群多样性迅速下降,容易陷入早熟。PSO算法更注重于群体之间的学习,单个粒子对于周围环境缺乏自主搜索能力,算法后期如果陷入局部极值很难跳出。ACO算法是利用信息素的累积和挥发来指导个体寻优的,算法初期搜索盲目性大,收敛速度慢,后期也存在算法停滞的问题。AFSA中人工鱼个体在搜索的过程中,应用多种寻优行为,例如觅食、追尾、追尾等,可以很好地平衡探寻新解域和精细搜索当前解域这两种不同的搜索模式,所以具有良好的克服局部极值的能力,在求解MKP问题中取得了优于GA、PSO算法以及ACO算法的效果[17-19]。

本文针对AFSA在求解大规模MKP时存在算法后期收敛速度慢、搜索精度低的问题,提出了一种针对大规模多背包问题的高级人工鱼群算法(advanced artificial fish swarm algorithm for large scale multiple knapsack problem,AAFSA-LMKP)。本文算法通过改进AFSA的初始化方式,优化人工鱼个体的行为算子,加快了算法的收敛效率。同时,引入视野和步长这两个参数的动态调整,添加人工鱼微调策略使算法的精度显著提高。大量的仿真实验数据表明,该算法提高了大规模多背包问题求解的速度和精度。

1 相关背景介绍

1.1 MKP

MKP的数学模型可描述为

xij∈{0,1},i=1,2,…,n;j=1,2,…,m

(1)

式中,n和m分别表示物品和背包的数目;pi表示第i件物品的价值;wi表示第i件物品所需要的容量;cj表示第j个背包的容量限制;pi,wi和cj均为大于0的值;当xij等于1时表示第i件物品被放入第j个背包内,等于0时表示未放入。

1.2 AFSA

AFSA通过对大自然中鱼的行为(即随机游动,觅食,追尾以及聚群)的简单模拟,来指导人工鱼在解空间内尽可能的搜索最优解。图1是人工鱼模型的简单示意图。假设当前人工鱼的状态为X,Visual表示其视野范围,在Visual范围内的人工鱼定义为其伙伴,伙伴之间可以互相交换彼此间的信息,例如食物浓度,当前位置等。Step表示人工鱼在一次寻优行为中所能达到的最大步长。

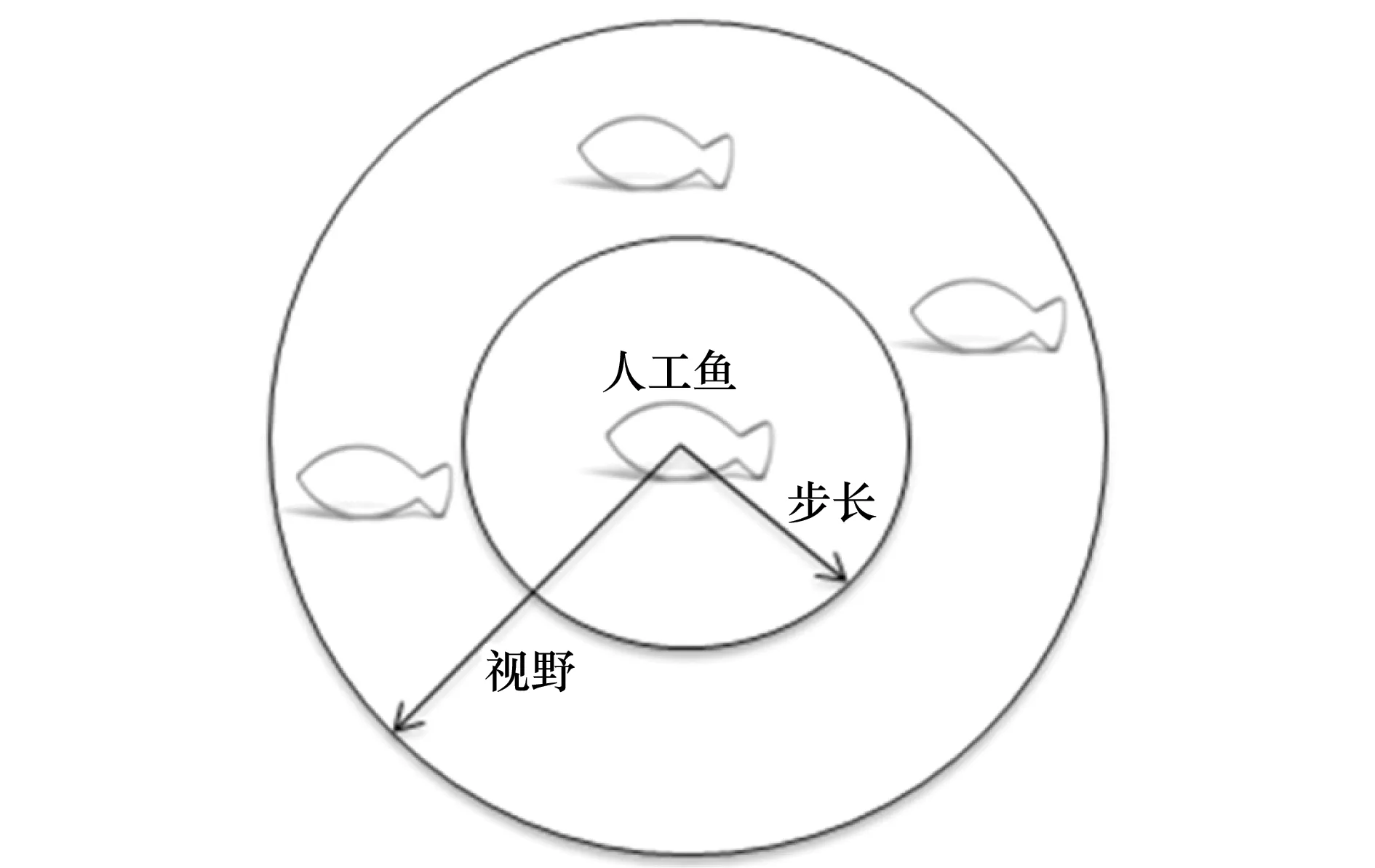
图1 人工鱼模型示意图Fig.1 Sketch of artificial fish model

人工鱼的4种行为中,随机游动和觅食行为为开发新的解状态提供了可能,保证了算法的收敛性。而追尾行为提高了收敛的速度,同时聚群行为保证了算法的稳定性。根据文献[17,20]的理论证明以及文献[21]的优化经验,可以发现适当简化人工鱼的行为对于算法的全局收敛性不会产生影响,所以本文只选取随机游动,觅食和追尾3种行为来进行寻优搜索。

本文人工鱼个体的寻优行为描述如下:

(1) 随机游动:人工鱼当前状态为Xi,在Step的限制内,随意向其他方向前进。

(2) 觅食行为:人工鱼当前状态为Xi,在Visual范围内,随机选取任一状态Xj,如果Xj的适应值满足Yj>Yi,则在Step的限制内,向Xj方向前进。否则在规定次数内重新选择新的状态Xj,超过规定次数找不到符合条件的Xj执行随机游动。

(3) 追尾行为:人工鱼当前状态为Xi,在Visual范围内,找到状态最优的伙伴Xmax,判其适应值Ymax>Yi并且周围不太拥挤(nf/N<δ),则在Step的限制内,向Xmax方向前进。

1.3 人工鱼编码

目前,针对MKP问题的编码问题有3种:01编码[22]、组编码[23]以及多值编码[11]。对于本文的MKP,01编码的解空间个数为2m×n,随着n和m增大,解空间呈指数级增长,而且在这个巨大的解空间中,存在相当多的将1个物品放入2个甚至多个背包的非法解,例如{{0,1},{1,1}}是01编码解空间的1个解,代表的是第1个物品放入第2个背包,而第2个物品被同时放入第1个背包和第2个背包,这显然是不符合常理的。而组编码在求解过程中,会出现多个解表达不同而含义相同的情况,例如{(1,5,6),(3,4)}与{(6,5,1),(4,3)}这两个解编码不同,但都是代表第1,5,6个物品放入第1个背包,第3,4个物品放入第2个背包的情况,这样对于搜索过程是不利的,会导致重复搜索。本文采用多值编码方式。相比前两者,多值编码方式不但极大地缩小了解空间(解空间为mn),解码简单并且具有唯一性,同时也杜绝了非法解的产生。

对于拥有n个物品和m个背包的多背包问题来说,创建数组X=(x1,x2,…,xn),xi∈{0,1,2,…,m},i=1,2,…,n。xi表示第i个物品的放置情况,xi=0表示此物品未放入任何背包。例如:X=(1,3,1,2,0)表示第1件物品和第3件物品被放入第1个背包中,第2件物品被放入第3个背包中,第4件物品被放入第2个背包中,而第5件物品未放入任何背包。

1.4 适应值计算及约束处理

AFSA优化是依靠概率进行搜索的,需要评价函数计算人工鱼的适应值后确定个体的优劣。本文的多背包问题的评价函数可以设计为

s.t.xi∈{0,1,…,m}

(2)

式中,pi表示第i件物品的价值;xi表示第i个物品被放入的背包编号,xi=0时表示物品未放入任何背包。

众所周知,MKP问题是一个具有多个约束的组合优化问题。在实际应用中,因为问题的复杂性和规模不断扩大导致约束个数增加,问题的求解难度也会骤然增大。所以,如何妥善的处理约束成为了求解MKP问题的关键。罚函数法[24]的性能很大程度依赖于惩罚系数的设置,而且当非可行解数目很多时很难提升算法效果,针对这些缺陷,学者们又提出了拒绝非可行解法以及修复非可行解法[25],这两种方法都是将不满足约束的非可行解转化为可行解,但是对于非可行解的处理有很大的随机性。根据文献[26]中的理论分析,有约束问题的最优解基本都在约束边界附近,所以需要对非可行解进行针对性的修复。本文算法在求解过程中产生非可行解后,根据单位价值密度由低到高依次取出物品直到将其修复为可行解,对于修复后离约束边界较远的个体,通过执行调整策略可以使个体尽量靠近约束边界,调整策略具体实现将在下章详细阐述。

2 AAFSA-LMKP在大规模MKP中的应用

2.1 基于单位价值密度的人工鱼初始化方法

AFSA在初始化人工鱼时一般采用随机生成的方式。根据第1.4节中的分析,为了提高算法的收敛性,在初始化时应该尽可能的使人工鱼分布约束边界附近。为了达到这个目的,本文提出了一种基于单位价值密度的人工鱼初始化方法。

具体做法是:假设第i件物品的单位价值密度为pdi,首先将n个物品的pd按数值从大到小排序存入单位价值密度表pd[n]中,初始化人工鱼时,从单位价值密度最高的物品开始,按表中顺序依次为当前物品随机产生1个整数Bag_num(0≤Bag_num≤m),如果Bag_num=0,则表示当前物品不放入背包,否则判断第Bag_num个背包剩余容量是否足够放入物品,是就将物品放入背包,背包剩余容量减少放入物品相应的w值,并将已经放入背包的物品标记;当背包容量不够时,则不放入背包。重复以上步骤,直到所有的背包物品放置完毕。这样的做法可以使单位价值较大的物品尽可能多地放入背包中,同时保证了初始化人工鱼的物种多样性,从而提高初始化人工鱼的适应值。

本文人工鱼初始化的伪代码如下:

AF_Initialization():

fori←1 ton∥遍历背包单位价值密度表

Bag_num=Rand(0,m);

∥0为不放入,否则选择第Bag_num个背包

if(cBag_num>pd[i] &&pd[i].Flag==-1)

∥背包剩余容量足够并且物品未被放入其他背包

PutInto(pd[i],Bag_num);

∥物品被放入背包

cBag_num=cBag_num-pd[i].w;

∥重新计算背包剩余容量

pd[i].Flag=1;

∥标记物品已被放入背包

end if

end for

2.2 追尾行为以及行为选择的优化实现

对于大规模的组合优化问题,解空间非常大。人工鱼初始化后其分布可能会非常稀疏,很有可能会出现所有人工鱼在视野范围内都没有伙伴的情况,只能转而执行觅食和随机游动行为。但是追尾行为是人工鱼在算法前期快速收敛的关键,快速收敛需要让人工鱼快速地游到适应值较高的区域,所以本文改进了人工鱼追尾行为和行为选择的具体实现,以提高算法的快速性。

当人工鱼个体执行追尾行为之前,先判断视野内有无伙伴符合追尾的条件,如果存在,直接向此伙伴方向前进;否则直接向公告板记录的历史最优解方向前进。为了避免公告板的状态周围过于拥挤以及算法后期震荡,人工鱼步长采用随机步长。修改后的追尾行为描述为:人工鱼当前状态为Xi,向Xbulletin方向前进Rand(1,step)距离。伪代码描述如下:

AF_Follow():

if (Neighbor!=NULL &&YNeighbor>Yi&&nf/N<δ)∥存在伙伴符合追尾条件

Xi|next=Xi+Rand(1, step)·(XNeighbor-Xi)

∥向追尾伙伴方向前进随机步长

else

Xi|next=Xi+Rand(1, step)·(XBulletin-Xi)

∥向公告板方向前进随机步长

end if

传统的AFSA行为选择(Behavior_Strategy)是分别执行人工鱼的每种行为,然后从多个执行结果中选择适应值结果最高的来执行。这样的做法是非常耗时间的一种处理方式。本文的行为选择具体实现是让人工鱼优先执行追尾行为,然后再次执行觅食行为,这样的做法即可以让人工鱼快速聚拢到食物浓度高的区域,又能避免人工鱼太过密集导致拥挤现象的出现。

2.3 视野与步长的动态调整方案

目前有很多关于动态调整视野和步长的研究,做法都是随着搜索的进行,逐渐减小这两个参数的值[27-29]。但在搜索的过程中,每个人工鱼个体所处的区域不同,这样一刀切的做法会存在两个弊端:算法前期在较优解区域的人工鱼可能会因为视野和步长过大而跳出当前的搜索域,而后期因为拥挤度因子没有进入较优解区域的人工鱼会在较差解域内做无意义的精细搜索。所以,根据人工鱼个体当前情况来动态地调整Visual和Step值是非常有必要的。

根据以上的分析,当人工鱼当前适应值较高时,就可以假设它当前处于较优解区域内,此时应该采用较小的Visual和Step值来促使人工鱼对于当前解区域进行细粒度的精密搜索;如果人工鱼当前适应值低,可以推测当前所处的解区域搜索价值较低,应该提高Visual和Step值来指导人工鱼尽快游出这片区域,开发新的解区域重新搜索。

Visual和Step值可按式(3)实施动态调整。

(3)

式中,n为物品数目;Xi.Fitness表示人工鱼当前的适应值；Bulletin.Fitness表示公告板记录的适应值。

2.4 针对MKP的人工鱼调整策略

对于MKP问题来说,背包剩余容量越小越好。人工鱼每次执行完搜索行为的时候,肯定会有一部分物品从背包中被拿出,这样背包剩余容量发生变化后,为了提高寻优的精度,我们需要对于人工鱼当前的背包分配方式进行略微调整,检查是否还有背包的剩余容量足以放入未放置的物品。具体实现为:从第1个背包开始,遍历单位价值密度表,检查是否有未放入的物品重量小于背包剩余容量,如果有满足条件的物品,将物品放入此背包,更新背包剩余容量,标记物品已被放入背包,否则换下1个背包。重复以上步骤,直到所有背包的剩余容量都不够放置任何未放置的物品。

2.5 算法流程

求解大规模MKP问题的优化AFSA算法具体实施流程如下:

步骤1设置AFSA基本参数:种群规模Popsize,尝试次数Trynumber,拥挤度因子δ;基于单位价值密度来初始化人工鱼种群,计算AF适应值并更新公告板;

步骤2根据式(1)调整人工鱼当前的Visual和Step值;

步骤3AF执行行为选择,先追尾再觅食,在搜索行为后应用人工鱼调整策略更新AF状态;

步骤4AF更新适应值与公告板比较,如果适应值优于公告板记录的值,则更新公告板,否则转向步骤5;

步骤5判断是否达到算法终止条件,如果达到则终止算法进程,否则跳转至步骤2。

3 数值实验及算法有效性测试

为了验证本文算法的有效性,针对大规模多约束MKP问题,分别比较了文献[17]中的标准AFSA(std.AFSA)、文献[26]的优化AFSA(ASR-AFSA)以及本文提出的AAFSA-LMKP的寻优精度及寻优速度。本文算法以及对比算法都使用C++语言实现,在PC机(CPU Inter Core i5-4460,主频3.2GHz,RAM 8GB)上运行。对比算法的主要参数设计如下:Popsize=20;Visual=20;Step=10;Trynumber=300;δ=0.618。本文中视野和步长由式(3)确定,其他参数与对比算法一致。

文中使用了文献[26]中约束较多(m=50,n=200、500、1 000)的数据来测试算法的寻优效果。物品重量及价值数据包含了3种类型:非相关数据,弱相关数据以及强相关数据。每组中又根据数据生成范围被分为3组(R=100,1 000,10 000)。背包容量数据分为2种:相似数据和非相似数据。具体数据生成方式如下:

(1) 物品重量及价值数据

①非相关数据:pi和wi在[10,R]中随机生成;

②弱相关数据:wi在[10,R]中随机生成,而pi在[wi-R/10,wi+R/10]中随机生成;

③强相关数据:wi在[10,R]中随机生成,而pi被设置为wi+10。

(2) 背包容量数据

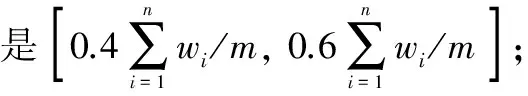
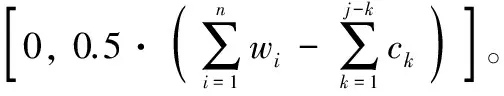
由于篇幅原因,本次测试数据无法在文中详细列出,测试数据可在https:∥github.com/DBEngine/MKP/tree/master/data下载。

由于测试算法在搜索行为中存在随机性,为了消除其对于实验结果的影响,本次实验结果均为10次寻优迭代过程的平均值。因为每个算法的复杂度不一致,每次迭代时间也会不同,所以我们在实验中使用时间作为算法完成条件。表1是3种测试算法在7 s内搜索到的最优解,“----”表示最终结果为非可行解。

由表1可以看出,本文算法在仿真测试中寻优精度表现基本都超过了对比算法,仅有1个实例未超过但接近文献[26]中的算法。而std.AFSA在有些实例中因为罚函数参数设置问题,甚至在一些测试实例中未能求得可行的解。

为了更直观的证明本文算法对于大规模MKP问题求解的有效性,又测试了1组更大规模的多背包数据(m=100,n=2 000)。3种测试算法的寻优效果如图2所示,可以看出本文算法的寻优性能具有明显的优势。因为应用了改良的初始化方式,收敛初值较另外两种算法大大提升。在算法前期,对比算法由于追尾行为条件的限制,初期速度较慢,而本文算法由于借鉴了公告板的的优良记录,能够引导更多的人工鱼向较优的区域方向前进,所以收敛效率更高。

表1 m=50, n=200、500、1 000 7 s内的仿真结果

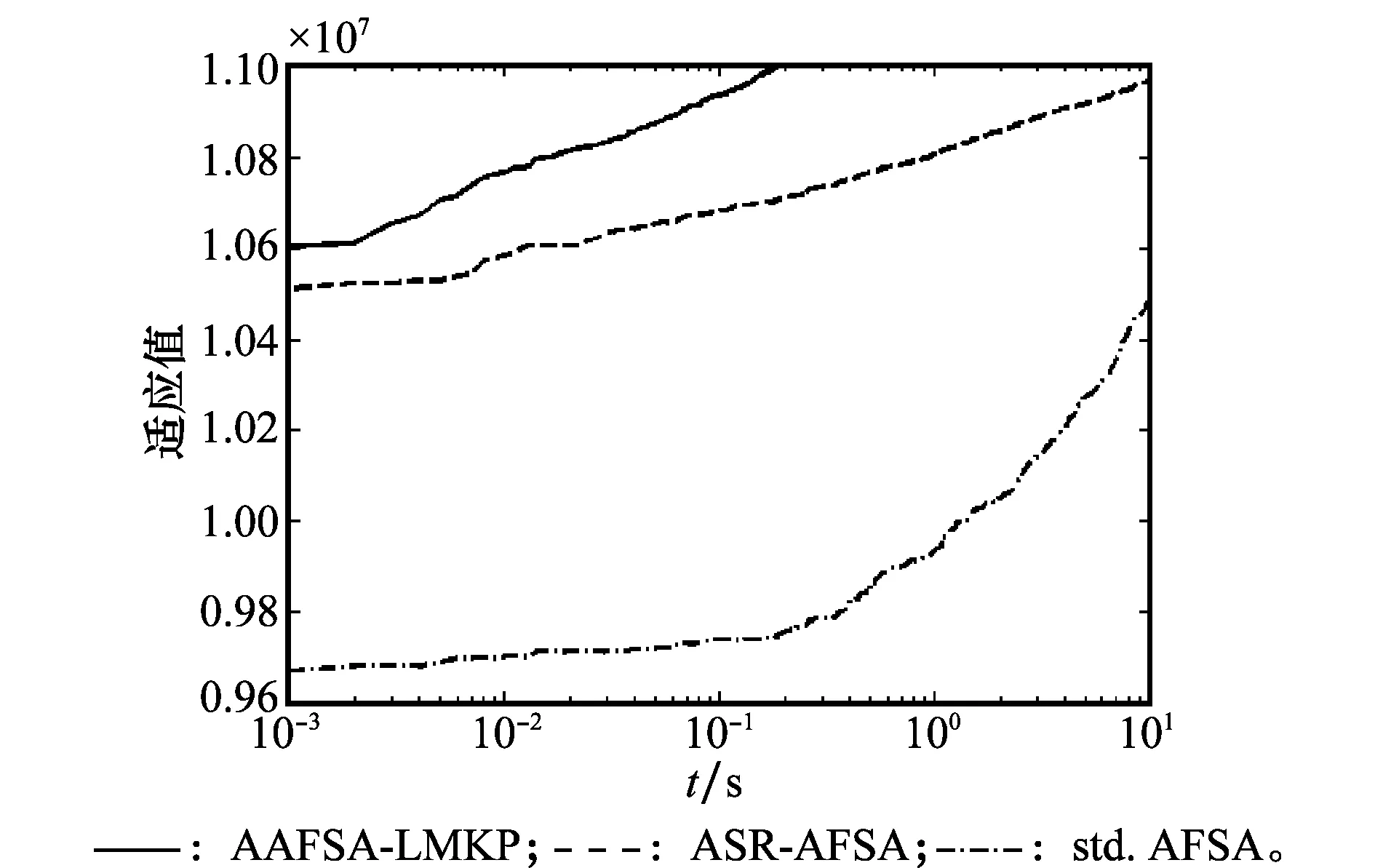
图2 3种算法进化曲线对比Fig.2 Evolution curve comparison of three algorithms

为了验证本文动态调整视野和步长方案的有效性,对比了视野和步长的3种设置方式,分别是文献[17]中的标准AFSA(std.AFSA)的静态设置方案、文献[29]的高级AFSA(AAFSA)的渐变设置方案以及本文AAFSA-LMKP的动态设置方案,算法其他步骤与本文算法保持一致,进化曲线如图3所示。由图3可以看出,本文算法在收敛速度和精度上较对比算法有了明显的提升。std.AFSA因为采用了静态的视野和步长,算法初期很难快速的引导人工鱼个体向适应值较高的区域靠拢,而后期也会因为步长过大容易错过最优解导致精度不足。文献[29]中视野和步长的设置方案确实在一定程度上提高了寻优性能,但是与本文的视野步长动态调整方案相比,少了对于公告板信息的借鉴,所以求解速度和精度上还是表现不佳。因为AFSA本质上的随机性,可能在初期就有少量人工鱼已经靠近最优解,对于这些人工鱼个体来说,在当前区域内精细搜索才是最佳选择。同理,寻优后期也会有少量人工鱼因为拥挤度因子的影响而跳出了较优解区域,此时应当引导它们跳出当前区域开发新的解域或者重新进入已知的较优解域。

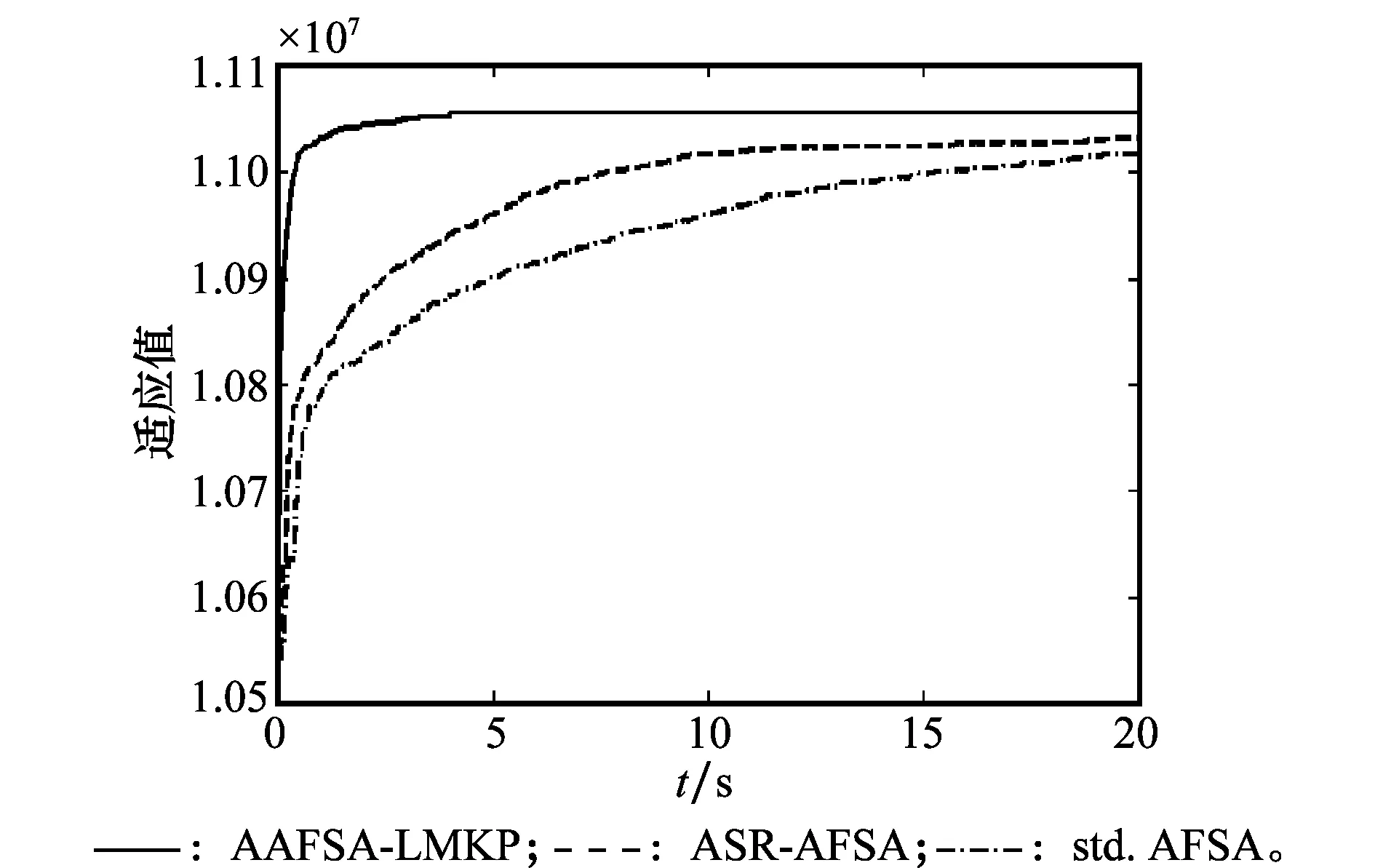
图3 3种视野步长设置方案进化曲线对比Fig.3 Evolution curve comparison of three setting strategy of Visual and Step

图4展示了本文算法的3个参数:种群数目Popsize、尝试次数Trynumber和拥挤度因子δ对于算法性能的影响。可以看出,当Popsize设置较大时(Popsize=100),因为个体数量多,所以每代迭代耗时较长,前期收敛较慢,但是算法后期精度较高。从图3(b)可以看出,Trynumber设置的过小则会同时影响收敛效率和精度,根据实际算例测试结果,此参数最好设置在200～400。而δ参数的设置对于算法性能影响不大,综合考虑收敛效率和精度,建议设置在0.3～0.7。

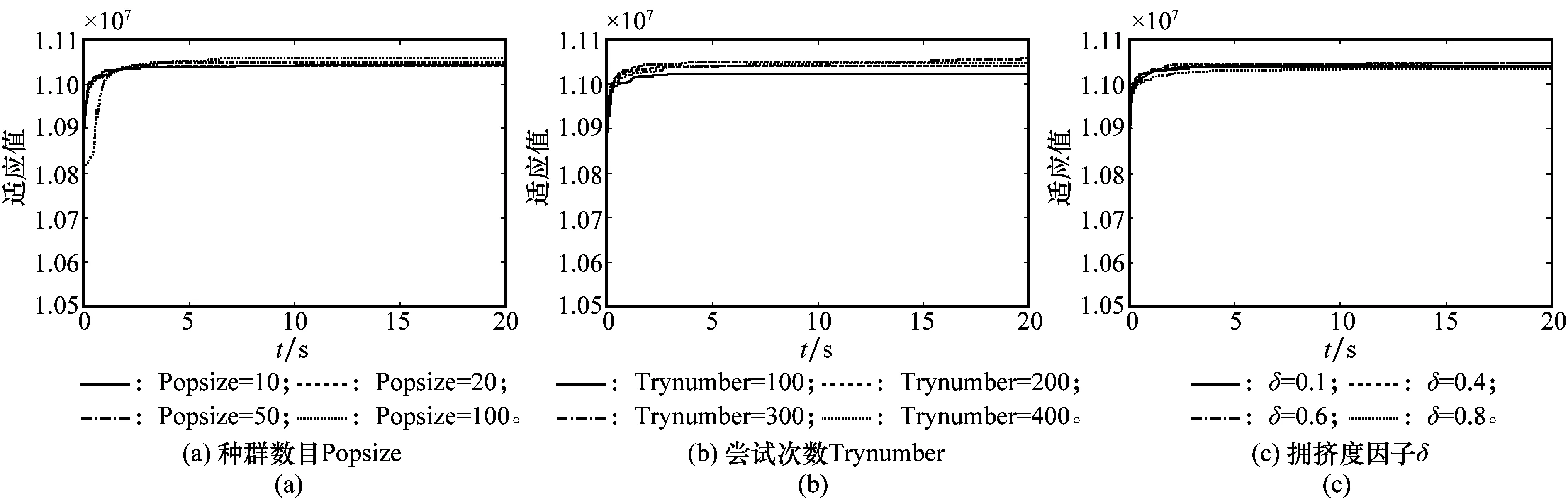
图4 人工鱼其他参数对算法性能影响对比Fig.4 Performance impact comparison of artificial fish’s other parameters

4 结 论

本文主要研究了大规模的MKP,针对其多约束以及解空间大的特点,提出了AAFSA-LMKP算法来求解此问题。针对现有算法求解速度慢的问题,AAFSA-LMKP改进了人工鱼个体初始化方法、追尾行为以及行为选择方式,保证了算法的收敛速度。同时,为了进一步提高算法的求解精度,引入了动态的参数设计和人工鱼个体调整策略。

为了有效分析AAFSA-LMKP对于大规模MKP的寻优能力,与现有的算法同时对多个测试实例进行了求解。实验数据表明,本文算法不仅较现有算法收敛速度更快,同时在算法后期,精度也有了很大的提升,并且随着多背包问题规模增加,AAFSA-LMKP性能提升更加明显。因为算法对于参数不敏感的特点,也避免了参数选择的麻烦。本文算法特别适用于多约束的大规模组合优化问题,如何利用AFSA个体在寻优过程中的独立性,利用现在的多处理器的硬件条件来并行实现进一步提升算法的寻优效率,将是笔者今后研究的方向。

[1] SONG X, LEWIS R, THOMPSON J, et al. An incomplete m-exchange algorithm for solving the large-scale multi-scenario knapsack problem[J].Computers & Operations Research,2012, 39(9): 1988-2000.

[2] 薛俊杰, 王瑛, 孟祥飞,等. 二进制反向学习烟花算法求解多维背包问题[J]. 系统工程与电子技术, 2017, 39(2): 451-458.

XUE J J, WANG Y, MENG X F, et al. Binary opposite backward learning fireworks algorithm for multidimensional knapsack problem[J].Systems Engineering and Electronics,2017,39(2): 451-458.

[3] 王凌, 王圣尧, 方晨. 一种求解多维背包问题的混合分布估计算法[J]. 控制与决策, 2011,26(8): 1121-1125.

WANG L, WANG S Y, FANG C. A hybrid distribution estimation algorithm for solving multidimensional knapsack problem[J]. 2011,26(8): 1121-1125.

[4] CHIH M C. Self-adaptive check and repair operator-based particle swarm optimization for the multidimensional knapsack problem[J]. Applied Soft Computing, 2015, 26(1): 378-389.

[5] VARNAMKHASTI M J. Overview of the algorithms for solving the multidimensional Knapsack problems[J]. Advanced Studies in Biology, 2012, 4(1): 37-47.

[6] PUCHINGER J, RAIDL G R, PFERSCHY U. The multidimensional knapsack problem: structure and algorithms[J]. Informs Journal on Computing, 2010, 22(2): 250-265.

[7] HOLLAND J H. Adaptation in Natural and Artificial Systems[M]. Cambridge: MIT Press, 1975.

[8] KENNEDY J, EBERHART R C. Particle swarm optimization[C]∥Proc.of the IEEE International Conference on Neural Networks. Honolulu: IEEE Press, 2002: 1942-1948.

[9] DORIG M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Trans.on Systems, Man and Cybernetics, 1996, 26(1): 29-41.

[10] BERBERLER M E, GULER A, NURIYEV U G. A genetic algorithm to solve the multidimensional knapsack problem[J]. Mathematical & Computational Applications, 2013, 18(3): 486-494.

[11] 宋海生,傅仁毅,徐瑞松,等.求解多背包问题的混合遗传算法[J].计算机工程与应用, 2009, 45(20): 45-48.

SONG H S, FU R Y, XU R S, et al. Hybrid genetic algorithm for multi-knapsack problem[J]. Computer Engineering and Application, 2009, 45(20): 45-48.

[12] YE J, LIU X D,HAN L. Evolutionary game algorithm for multiple knapsack problem[C]∥Proc.of the IEEE/WIC International Conference on Intelligent Agent Technology,2003: 424-427.

[13] SABET S, SHOKOUHIFAR M, FAROKHI F. A discrete artificial bee colony for multiple knapsack problem[J]. International Journal of Reasoning-based Intelligent Systems,2013,5(2): 88-95.

[14] KTARI R, CHABCHOUB H. Essential particle swarm optimization queen with Tabu Search for MKP resolution[J]. Computing, 2013, 95(9): 897-921.

[15] 马炫, 刘庆. 求解多背包问题的人工鱼群算法[J]. 计算机应用, 2010, 30(2): 469-471.

MA X, LIU Q. Artificial fish swarm algorithm for multiple knapsack problem[J]. Journal of Computer Application, 2010, 30(2): 469-471.

[16] 李迎,张璟,虎群,等.人工鱼群算法在虚拟机分配中的应用[J].计算机工程与应用,2015,51(4):22-28.

LI Y, ZHANG J, HU Q, et al. Artificial fish swarm algorithm for virtual machine placement[J]. Computer Engineering and Application, 2015, 51(4): 22-28.

[17] 李晓磊. 一种新型的智能优化方法-人工鱼群算法[D]. 杭州:浙江大学, 2003.

LI X L. A new intelligent optimization method-artificial fish school algorithm[D]. Hangzhou: Zhejiang University, 2003.

[18] ZHANG Y L, OGURA H, KUROIWA J. Fish swarm optimization method for the two-dimensional guillotine cutting pro-blem[J]. Journal of Signal Processing,2011,15(3):225-234.

[19] 黄光球,朱华平,周静.用鱼群算法求解石油运输系统多级站定位优化问题[J].系统工程理论与实践,2008,28(3):94-102.

HUANG G F, ZHU H P, ZHOU J. An optimization method of multistage stations locating in oil transportation based on fish-swarm algorithm[J]. Systems Engineering Theory & Practice, 2008, 28(3): 94-102.

[20] 黄光球, 刘嘉飞, 姚玉霞. 求解组合优化问题的鱼群算法的收敛性证明[J]. 计算机工程与应用, 2012, 48(10): 59-63.

HUANG G Q, LIU J F, YAO Y X. Global convergence proof of artificial fish swarm for solving combinatorial optimization problems[J].Computer Engineering and Application,2012,48(10): 59-63.

[21] LIU Q, ODAKA T, KUROIWA J, et al. An artificial fish swarm algorithm for the multicast routing problem[J]. IEICE Trans.on Communications,2014,E97.B(5):996-1011.

[22] 虞安波, 杨家本. 多背包问题的遗传算法求解[J]. 计算技术与自动化, 2002, 21(2): 59-63.

YU A B, YANG J B. Genetic algorithm for multi knapsack problem[J]. Computing Technology and Automation, 2002, 21(2): 59-63.

[23] FUKUNAGA A S. Dominance in incomplete solvers for the multiple knapsack problem[C]∥Proc.of the IEEE World Congress on Computational Intelligence, 2003: 2225-2232.

[24] COELLO C A C. Use of a self-adaptive penalty approach for engineering optimization problems[J]. Computers in Industry, 2000, 41(2): 113-127.

[25] SALCEDO-SANZ S S. A survey of repair methods used as constraint handling techniques in evolutionary algorithms[J]. Computer Science Review, 2009, 3(3): 175-192.

[26] LIU Q, ODAKA T, KUROIWA J, et al. A new artificial fish swarm algorithm for the multiple knapsack problem[J]. IEICE Trans.on Information & Systems,2014,E97.D(3):455-468.

[27] 王联国,洪毅,施秋红.全局版人工鱼群算法[J].系统仿真学报,2009,21(23):7483-7486.

WANG L G, HONG Y, SHI Q H. Global edition artificial fish swarm algorithm[J].Journal of System Simulation,2009,21(23): 7483-7486.

[28] 周燕云, 许国军, 覃锡忠,等. 基于改进人工鱼群算法的蜂窝网络信道分配[J]. 计算机仿真, 2013, 30(6): 206-209.

ZHOU Y Y, XU G J, TAN X Z, et al. Channel assignment in cellular network based on improved artificial fish school algorithm[J]. Computer Simulation, 2013, 30(6):206-209.

[29] 桓自强,倪宏,胡琳琳,等.AAFSA-RA:一种采用高级人工鱼群算法的多资源分配方法[J].西安交通大学学报,2014,48(10):120-125.

HENG Z Q, NI H, HU L L, et al. AAFSA-RA: A Multi-Resource Allocation Method Based on an Advanced Artificial Fish Swarm Algorithm[J]. Journal of Xi’an Jiaotong University, 2014, 48(10): 120-125.