基于K-means算法的优化及在航空业客户细分的应用

赵倩芸，李拥军

（1.华南理工大学数学学院，广州 510006；2.华南理工大学计算机科学与工程学院，广州 510006）

0 引言

随着互联网技术的快速发展，各行业实现信息化服务已成为大势所趋，当然，航空行业也不例外。目前，我国航空业的电子信息系统已较为健全，同时，各个航空公司的数据库中也都存有大量的包含旅客身份信息以及出行行为信息的统计数据[1]，但是这些数据就如同“散沙”般堆在数据仓库中，随着时间的日积月累，数据量也越来越大，在对客户进行细分时，传统的K-means算法在K值选取以及聚类中心方面存在缺陷，针对此进行优化改进，提出了Canopy-Kmeans算法。本文通过改进的聚类算法将客户细分，以便于为公司的市场营销活动创建有针对性的便于管理的分组，并且可以识别各客户分组的属性与需求，比较不同细分群体的特征，从而确定针对各细分客户的特定行动，最终开发适合航空业务部门使用的“客户分群模型”，在为客户提供更好服务的同时，也为提高公司的效益以及进一步的发展做出贡献。

1 K-means算法聚类

聚类是数据挖掘领域中的一种技术，是各企业进行客户细分比较常用的方法，它把一个没有类别标签的样本集按照某种准则划分成若干个子集，使得相似的样本尽可能被归为一类，而不相似的样本尽量被划分到不同类别中。在多种聚类算法中，最著名的一个算法便是K-means（K均值）算法，它也是最常被用于进行客户细分的聚类方法。K-means聚类是由Mac Queen在1967年提出的一种实时无监督的硬聚类算法，此算法假定在欧氏空间下，并且以最小化误差函数为约束条件，将数据对象划分为k类（k为预先给定的）[2]，算法的初始中心点是随机选取的，具有很大的随机性和盲目性，一旦选取不好，会直接影响聚类效果，选取欠佳时，同样会使得算法运行时间过长，影响算法的执行效率。K-means算法的伪代码如下：

从K-means算法的思想和伪代码可以看出算法的时间复杂度为：

O（nkd）=所有对象数目*聚类簇数*迭代的总次数

其中，n表示所有数据对象的数目，k表示聚类的簇数，d则代表迭代的总次数。这便意味着：

算法的时间复杂度与聚类簇数k成正比。而在实际应用中，k的选取一般都是凭借经验以主观意愿为主的，当k的值过大时，时间复杂度会很高，直接影响算法效率，当k过小时，又会有损聚类的准确度。这个标准很难把握。

算法的时间复杂度还与数据对象的总数目n成正比。当要处理的数据量过大时，不可能将所有的数据同时加入内存进行处理，只能在硬盘与内存之间频繁交换，这就使得算法效率降低，耗费系统资源过多[3]。

由于航空公司提供的数据量相对较大，K-means算法的多次迭代，必然会使得算法的效率不够高，为了提高效率，将K-means进行优化实现，便十分有必要了。

2 改进算法：Canopy-Kmeans算法聚类

2.1 Canopy算法

Canopy算法是从数据集中随机选取一个数据对象A，计算数据对象之间的距离确定相似性，将距离小于等于阈值T1（即数据对象之间相近）的数据对象划分到同一个Canopy区域中，同时，距离比阈值T2小的数据点将不能再作为下一个数据子集Canopy的中心点，其中，T1＞T2。这样，便生成了若干个Canopy子集（如B、C、D、E），这些 Canopy子集允许有交集，即每个数据对象可以同时归于一个或多个Canopy子集，但是，每个Canopy子集必须至少包含一个数据对象。

算法步骤如下：

（1）将所有的数据对象预处理后放入一个集合D中，选取距离阈值T1和T2，其中，T1＞=T2；

（2）从数据集合D中随机选取一个数据点P，计算P与所有Canopy子集中心点间的距离（若Canopy子集不存在，则将数据点P作为一个新Canopy的中心点，同时加入到Canopy中心点列表中，然后将其从集合D中删除），若P和某个Canopy中心点之间的距离小于或等于T1，则将P加入到此中心点所属的Canopy中；

（3）当数据对象P和某个Canopy的中心点之间的距离小于等于T2时，将此数据对象从列表D中删除，因为此时，它与这个Canopy很接近，不适合再作为其他Canopy子集的中心点；

（4）反复迭代此过程，重复执行（2）-（3），直到集合D为空时，迭代过程结束。

2.2 Canopy-Kmeans算法

本次研究选用Canopy算法来对传统的K-Means算法做出优化[4]，即改进后的Canopy-Kmeans算法，Canopy-Kmeans算法不需要我们人为地给定K值，会根据自身的迭代主动聚成类簇，因此可以先用Canopy算法对数据预处理，将得到的Canopy中心点直接作为聚类的初始中心点，这在某种程度上解决了传统的K-means在k值以及初始中心点的选取方面的问题[5]，从而提高算法的迭代效率和准确率。

本文将此优化后的算法称为Canopy-Kmeans算法，该算法分为两个部分：首先，由Canopy算法进行粗聚类，将数据集分为k个Canopy，每个Canopy都有一个中心点；其次，用K-means算法进行细聚类，将第一步产生的Canopy中心点直接作为聚类初始中心点，在每一个Canopy中使用K-means算法计算数据点和中心点的距离，将数据点重新归类。其详细聚类步骤如下：

Canopy-Kmeans算法步骤

（1）将所有的数据预处理后放入集合D中，选取距离阈值：T1、T2，其中 T1＞T2;

（2）从数据集合D中随机地选取一个数据点作为第一个Canopy的中心点，并将其从集合D中去除；

（3）计算D中其他的数据点和全部的Canopy子集中心点之间的距离，如果得到的距离小于等于T1，则将这个数据对象加入到此中心点对应的Canopy子集中。若距离小于等于T2，则将这个数据对象从集合D中删除。若距离大于T1，则将这个数据点作为一个新的Canopy中心点，加入到中心点列表中。

（4）重复迭代步骤（3），直到数据集合D为空集。通过以上几步可以将集合D中的所有数据点划分为k个Canopy子集，其中，每个数据点可以属于一个甚至多个Canopy，并且k个Canopy包含所有的数据点，没有数据孤点。

（5）将前面产生的k个Canopy中心点作为k个初始聚类中心点。

（6）由于k个Canopy子集之间是可能存在交集的，一个数据点可能同时属于多个Canopy，所以应该将这样的数据点划分到离它最近的Canopy子集中。即需要计算每个Canopy中全部数据点和Canopy的中心点之间的距离。

（7）更新每个Canopy的聚类中心点（每个Canopy中所有数据对象的平均值）。

（8）计算新的类簇中心点和最初的Canopy中心点之间的距离，若此距离小于等于T1，则将这个新类簇中心归入到对应的Canopy子集中。

（9）当聚类标准函数收敛（新中心和旧中心的距离小于某个预先给定的阈值）时，退出迭代，否则重复执行步骤（6）-（8）。

将Canopy中心点集合记为：CanopyCenterList=C（C1、C2、...、Ck）,聚类中心点的集合记为：P（P1、P2、...、Pk），下面给出Canopy-Kmeans算法的伪代码，如下：

3 实例分析

为了测试传统的K-means算法和优化后的Cano⁃py-Kmeans算法的准确率以及计算效率，我们采用机器学习标准测试数据库UCI[6]（UCI Machine Learning Repository）中的两个数据集Seeds和Car Evolution来做实验，这些机器学习数据集是完全公开的，可以根据需要在网站上下载。它们的数据特征如表1所示。

表1 实验数据集特征表

Seeds数据集是含有210个实验样本的小麦种子样例，每个样本有7个属性，并根据种子的特征分为三个不同类别：卡玛、罗萨以及加拿大；Car Evolution数据集是包含1728个实验样本的汽车样例，每个样本有6个属性，并分为四个类别：unacc、acc、good以及 vgood。两个数据集都是标准数据集，所以我们暂不对其进行预处理，直接用原始数据进行实验。

由于本次试验的主要目的在于比较传统K-means算法和优化后的Canopy-Kmeans算法的准确性以及运算效率，所以实验选择在Spark平台上采用单机模式进行，在seeds数据集上，将传统的K-means并行算法的迭代次数设为10次，将类别k设为3，将优化后的Canopy-Kmeans算法的阈值T1和T2分别设为9和6；在Car Evolution数据集上，将传统的K-means并行算法的迭代次数设为10次，将类别k设为4，将优化后的Canopy-Kmeans算法的阈值T1和T2分别设为8和6。

另外，本实验选取聚类结果的准确率以及最小误差平方和作为评价这两种算法的准确性标准，其中，准确率是将实验得到的聚类结果和UCI标准测试集中的类别标签做对比计算出来的（我们采用的Seeds和Car Evolution数据集都是带有类别标签的），其定义如下：

其中mi是最后的聚类结果中被正确分到第i类的数据对象的个数，k是最终类别个数，n是所有的数据对象个数。最小误差平方和Jmin则表示聚类多次迭代结束后的误差平方和Js中的最小的一个，误差平方和公式定义如下：

其中，s表示聚类的类别数目，nk表示第k个类别中的对象数目，表示第k个类中的第j个数据对象，mk则表示第k个类别的聚类中心点，另外，算法的运算效率则直接采用两种算法聚类结果完成时分别耗用的时间t。最终的实验结果如表2所示。

表2 传统K-means算法和优化后的算法的结果对比表

通过表2中的实验结果，我们可以得到：一方面，由于Canopy-Kmeans算法先用Canopy方法粗聚类得到若干个Canopies，然后只在每个Canopies区域内部计算每个数据点与Canopy中心点间的距离，而不用像传统K-means算法那样，必须迭代计算全部的数据点和每一个中心点的距离，因此优化后的算法所用时间更少、效率更高；另一方面，优化后的算法使用Canopy方法进行预处理，将Canopy中心点直接作为聚类的初始中心点，这在一定程度上解决了K-means算法K值以及初始点的选取问题，因此准确率也会相对有所提升。这就证明了我们优化的模型Canopy-Kmeans的可用性。

4 数据整理与特征构造

通过航空公司的数据接口直接读取数据集市中的数据，对原始基础表进行清洗、合并，作为聚类模型的初始训练集，部分实验数据字段如表3所示。

表3 部分实验数据的字段描述

在对合并汇总后的基本数据进行分析后发现，原始表中的数据虽然详细充足，但是涉及到的变量太多，难免会有一些不重要的因素影响聚类的结果，因此，在建模之前我们需要分析原始数据变量，构造并提取出对业务有用的衍生变量。通过对业务的充分理解与分析，并由航空业务领域的专家一起作出决策，决定从客户的订票行为、支付行为和乘机行为三个方面对用户进行细分，具体选取的建模变量如表4所示。

表4 衍生变量表格

5 细分结果及其分析

根据建立的模型，我们将处理后的数据在优化后的Canopy-Kmeans模型上进行客户细分，其中Cano⁃py-Kmeans算法中的阈值T1和T2分别设为0.9和0.4，模型最终将所有的客户一共分为8个群组，聚类结果如表5所示，其中，年龄、卡龄、现金支付比率、银行卡支付比率、其他方式支付比率、B2C订票比率、电话订票比率、平均折扣率以及两舱比率等21个字段对应的数据均为簇内所有数据对象的平均值。

根据聚类的结果，我们还可以得到各个分组中客户的分布情况，最少的占5%，最大的占24%，相对较均匀，具体如图1所示。

另外，由于我们利用Canopy-Kmeans算法模型对选取的18个业务指标变量进行聚类，是按客户的订票行为、支付行为和乘机行为来进行分群的，为了同时判断各组内客户的价值情况，我们需要分析每个组的RFM情况，具体情况如图2所示。

通过表5的客户细分结果、图1的客户群体分布以及图2每个组的RFM情况，总结出各群体优势特征和弱势特征，如表6所示。

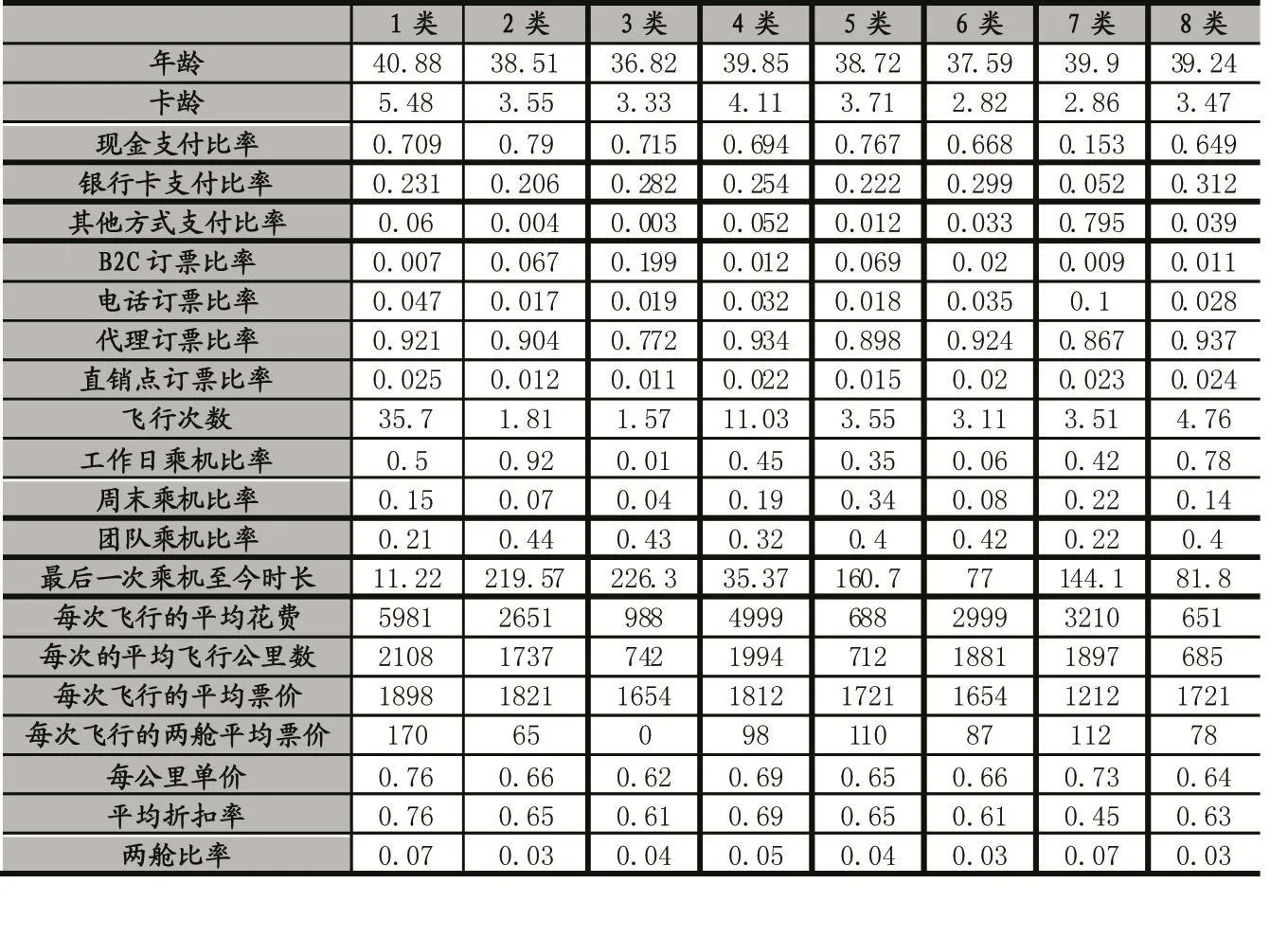
表5 客户细分结果表

图1 客户行为细分分布

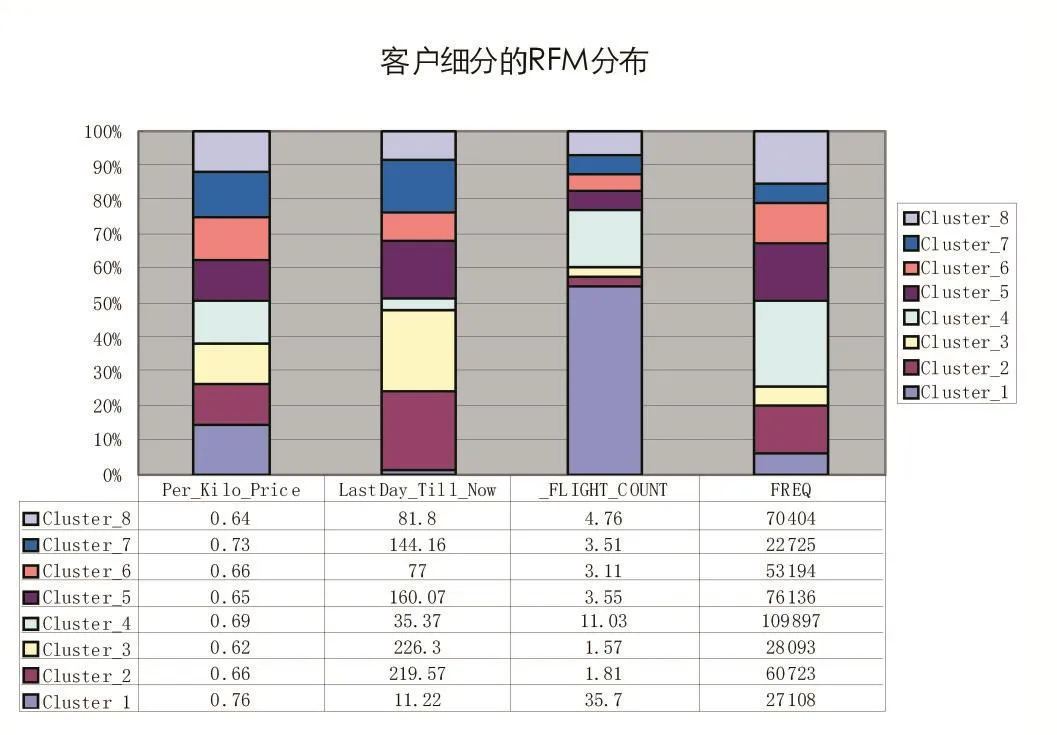
图2 客户细分的RFM分布

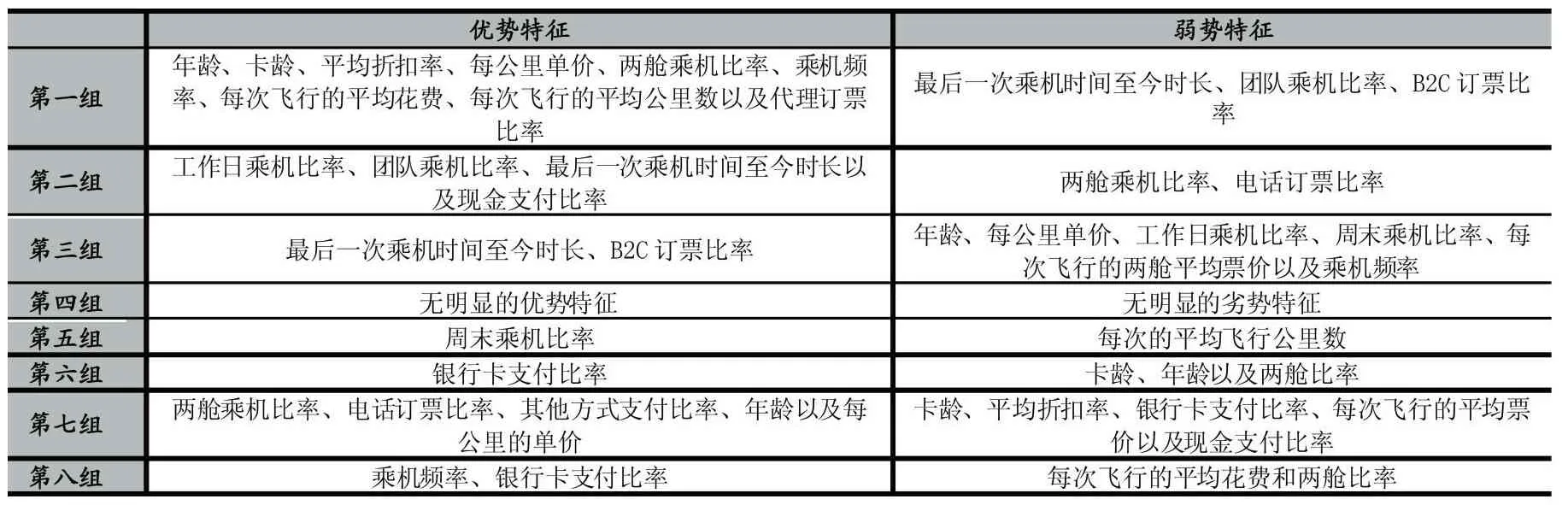
表6 各组优势特征和弱势特征

6 结语

本文采用优化后的Canopy-Kmeans算法结合选取的航空客户指标数据进行了客户分群，并且对客户细分的实验结果进行详细分析，结合各分群的RFM分布，对八个客户群进行业务上的解释并且通过以上相关分析，业务人员可根据分群结果以及客户细分的RFM分布作出合适的营销措施。

[1]杨鹏.基于数据挖掘的乘客出行行为研究[D].华南理工大学,2016.

[2]Verma M,Srivastava M,Chack N,et al.A Comparative Study of Various Clustering Algorithms in Data Mining[J].International Journal of Engineering Research and Applications（IJERA）Vol,2012,2:1379-1384.

[3]李飞,薛彬,黄亚楼.初始中心优化的K-Means聚类算法[J].计算机科学,2002,29（27）:94-96.

[4]McCallum A,Nigam K,Ungar L H.Efficient Clustering of High-Dimensional Data Sets with Application to Rfference Matching[C].ACM,2000:169-178.

[5]袁方,周志勇,宋鑫.初始聚类中心优化的K-means算法[J].计算机工程,2007,33（03）:65-66.

[6]UCI.Machine Learning Repository[EB/OL].http://archive.ics.uci.edu/ml/datasets.html.