云环境下基于非线性映射的保序加密方案

郁 鹏, 潘森杉, 张建明

(江苏大学 计算机科学与通信工程学院, 江苏 镇江 212013)

在已实现的云计算[1]服务中,隐私安全一直令人担忧,这已成为阻碍云计算发展和推广的主要因素之一.用户的数据隐私包括可用来识别或定位个人的信息(如电话号码等)、敏感的信息(如个人财务信息等).云计算的隐私安全问题[2]源于云计算数据外包和服务租赁的特点.用户数据存储到云环境中,人们失去了对数据的直接控制力,可能会导致个人隐私数据的泄露和滥用.而近年来发生的Google,MediaMax等云服务商泄露或丢失用户数据的事实证实了人们的担心.加密是一种常用的保护用户隐私数据的方法,但目前大多数的加密方案都不支持直接对密文的运算[3],如区间搜索、范围查询,因而严重妨碍了云服务商为用户提供更进一步的数据管理和运算服务,从而削弱了云计算的优势.

保序加密是一个保护加密值顺序的加密方案,可以使系统以与明文相同的方式在密文上执行顺序操作:一个数据库服务器能建立一个索引,所有加密数据都可以使用与明文数据相同方式来执行范围查询和排序,导致系统性能良好.这个优点使得可对已有软件进行最小的改变,使保序加密更容易被应用.但是顺序会给敌手更多的背景知识.假设敌手从其他数据提供者获取一些统计信息包括数据频率和数据分布.这样的敌手在保序数据隐私挖掘中总是被提到,但是在保序加密方案中还鲜有提及.敌手可以得到有用的统计信息来进行统计攻击.

在敌手的攻击中,假设敌手具有关于明文值或明文域上的统计信息的先验知识.以前的保序加密忽略这些类型的攻击或者假设攻击者没有关于明文域的任何信息.实际上,敌手在许多情况下可能具有关于明文域的基础信息或者更多的信息[4].

文中拟提出一个在外包数据库中可以抵抗统计攻击、实用、安全有效的保序加密方案.该方案中划分明文值区域成许多区间,允许一个整数在使用相同的密钥时能被加密成多个值从而抵抗统计攻击.

1 相关工作

1.1 云环境下加密

云环境下的加密有3个参与方: 数据拥有者、云服务器提供者和用户.而加密涉及的具体算法概括说包括4种: ① 系统建立算法，由数据拥有者运行,主要用来生成系统参数和数据拥有者的密钥.输入安全参数、数据拥有者生成系统的公开参数和自己的私钥.当涉及可搜索的公钥加密算法时,公开参数也包括数据拥有者的公钥. ② 数据加密算法，用来加密可搜索的数据.算法输入公开参数和数据明文,输出相应的密文(有时还会输出加密的数据关键词的索引表).如果是可搜索的对称加密算法,则算法还需输入数据拥有者的私钥. ③ 令牌生成算法，当用户需要搜索数据时,向数据拥有者提交搜索请求,然后数据拥有者运行该算法对请求进行响应.算法输入搜索条件和数据拥有者的私钥,输出一个令牌(token)或称为陷门. ④ 数据检索算法，用户利用该令牌逐一测试密文或索引是否满足指定的检索条件,仅当满足条件时,算法才输出相应的密文或者索引[5].

如果大数据加密之后存储,那么大数据以密文的形式存在,所以在密文搜索阶段不太可能会泄漏大数据的隐私[6-7].然而在这种情况下,为了保证大数据的可用性,必须要求对密文能够进行有效的检索和查询,所以本阶段的主要问题是如何设计能够满足大数据特点的可搜索的加密算法,即如何设计安全、运行效率高且允许对一般数据进行复杂搜索请求的密文搜索算法.

1.2 保序加密

保序加密最早由R. AGRAWAL等[8]在2004年提出,其核心思想为扩域映射,即将原数据映射到另一个大域空间中.保序加密的优点是可以对加密数据在无需解密的状态下直接进行比较操作,等值或者范围查询以及涉及MIN,MAX和COUNT的聚合查询.另一个加密方案有着可证安全保证(Boldy-reva′09)[9]:加密等价于保留顺序的随机映射.但是它的加密执行时间是176 ms,所以这个方案效率低.对于一个保序加密方案,可以达到的理想安全是IND-OCPA(Boldyreva′09):关于明文值除了它们的顺序外,不会再泄露更多的信息.达到理想安全的保序加密方案是可变保序加密(Popa′13[10],Kerschbaum′14[11]),这些方案通过建立包含所有加密明文值的二叉平衡树来工作,要求加密协议是交互的,并且对于已经加密的少量密文会随着新的明文值被加密而改变,用户可以自己定义函数来实现在数据库中的操作.这些功能严重地影响着方案的效率.除了以上的几种保序加密方案,一些其他的保序加密方案(Teranishi′14[12], Mavroforakis′15[13])也被提出,但是它们都除了值的数据还泄露了更多的信息[14].通过上面总结可以发现:为了达到高安全性,保序加密需要隐藏密文的顺序并且使用额外的功能来完成顺序比较,但是这种方法会导致低的效率,额外的存储空间并且不能直接密文比较.

1.3 线性加密技术和非线性加密技术

2013年,LIU D. X.等[15]首次提出线性加密的基本模型ax+b+noise,其中x是明文,a和b是密钥,noise是一个随机选择的值.但是这种线性加密模型没有安全保证,敌手可以利用重复型的数据来获取密钥.在极端情况下,选取重复数据的最大值和最小值来估计a的大小,当重复型数据越多,推测a的准确性越高.

针对这种情况,LIU D. X.等进一步提出了非线性加密模型af(x)x+b+noise,其中a>0;在x不等于0时,f(x)>0;在x1>x2>0或者x1f(x2).由于方程是非线性的,noise的取值范围会根据不同的输入值而不同,能很好地弥补线性加密的缺点,不会因为重复型数据而让敌手估计a的大小.

2 系统模型

2.1 问题模型

图1给出了保序加密基础模型.

图1 保序加密基础模型

如图1所示,保序加密模型反映了数据拥有者、云服务器提供者和用户之间的交互,具体过程如下: ① 用户用加密算法E对数据d进行加密,然后存储到云服务器上; ② 用户得到数据拥有者授权后,对搜索条件参数(para)进行加密,并且和计算要求(type)一起发送给云服务器; ③ 云服务器验证用户的权限,然后根据搜索条件得到搜索结果E(result)并返回给用户; ④ 用户对E(result)解密,得到相应的明文.

在这个过程中,因为保序加密的特点,云服务器可以对加密数据直接进行操作,那么产生了一个问题:用户和数据提供者对于敏感数据和参数进行怎样的加密处理,才能使数据隐私得到保护.如果这个问题不能得到有效解决,用户就不能利用云计算中的计算资源对敏感数据进行处理,从而削弱了云计算的优势.图2给出了问题模型示意图.

图2 问题模型

2.2 敌手模型

保序加密操作在客户端上执行,文中采取有效的方法来确保客户端上不会泄露任何关键信息.

假设有如下2种攻击者：

1) 消极的攻击者.它们有外包数据库的访问权限,能看到加密数据,除了顺序还想知道更多的信息,但是只能进行统计攻击.

定义1抗统计攻击.ε为一个加密算法,令Δ为明文值统计量∑p和对应密文值的统计量∑c的相似度统计;当Δ相当小时,可认为加密算法ε抗统计攻击.

2) 积极的攻击者.它们既有数据库访问权限又有客户端访问权限,有更多的信息来猜测加密的数据,能进行已知明文攻击或者选择明文攻击来猜测加密密钥.文中对选择明文攻击进行限制—IND-DNCPA(indistinguishabilityunderdistinctandneighboringchosenplaintextattack)[16].

定义2IND-DNCPA的安全性.敌手A发起以下攻击: ① 敌手A选择一组连续明文M={x1,x2,…,xk},xi∈D,xi≠xj且i,j∈[1,k],用加密算法进行计算得到相应的加密结果C={c1,c2,…,ck},A试图通过解方程的方式解出其他密文c(c∉C)对应的明文; ② 敌手A选择2个数据m0,m1,其中m1=m0+1,且m0∉M,m1∉M; ③ 加密算法随机加密其中一个数据mb，b∈{0,1},并将产生的密文cb返回给A; ④ 敌手A输出b′作为对b的猜测,则敌手A的优势概率定义为Adv(A)=|Pr[b′=b]-0.5|=ε.如果ε足够小可忽略不计,则算法是IND-DNCPA安全的.

实际上,现实中主要的威胁是第1种攻击者.它们能得到存储在外包数据库上的数据,但却不能得到加密密钥.所以抗统计分析攻击是文中基本和实际的安全目标.

3 新的保序加密模型

以下将介绍具体扩展密文的方法并且提出一个基于非线性映射的保序加密方案(nOPE).

3.1 概念

本节介绍文中将使用到的一些变量.

Di: 原始明文信息空间的一个区间,可以表示为Di=[li,ri].在2个相邻区间Di和Di+1,总是存在ri=li+1.

Ci: 扩展后的信息空间即密文空间中的一个区间,可以表示为Ci=[li′,ri′].在2个相邻区间Ci和Ci+1,总是存在ri′=li+1′.

Enc(): 从原始明文空间到密文空间的映射函数,是一个单调递增函数,由不同区间Di的Enci(x)组成.

Range(i): 用以获得原始明文区间Di的最大值和最小值的函数.

Range′(i): 用以获得密文区间Ci的最大值和最小值的函数.

Index(i): 用以获得值x在区间Di中的索引数i的函数.

3.2 保序加密构造

加密系统{M,C,k,Enc,Dec}含有明文空间M,密文空间C,密钥k,加密算法Enc和解密系统Dec.

保序加密方案通过以下几步执行: ① 随机划分原始明文信息空间成一系列不同长度的区间; ② 选择一个扩展的密文空间并且把密文空间划分成数量相同的区间; ③ 使用非线性加密功能来把原始数据映射到扩展的密文空间中去.

该保序加密方案具体如图3所示.

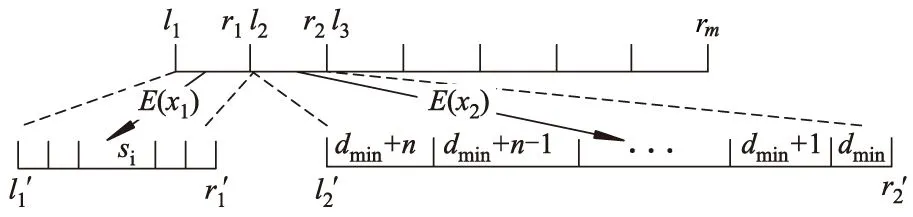
图3 保序加密方案

3.2.1 划分原始明文空间

与Liu′16[17]中的思想相同,将原始明文空间M划分成一系列的区间Di=[li,ri]，i=1,2,…,m,由于原始明文空间M通常是离散的空间,需要li,ri∈Z满足以下条件:

(1)

[li,ri]∩[lj,rj]=∅，i≠j.

(2)

这个步骤很有意义,有助于有效地破坏数据的分布规律:对于一个数据集,存在数据越多,划分成的区间数也就越多.

3.2.2 划分密文空间

将密文空间C划分成一系列的区间Ci=[li′,ri′]，i=1,2,…,m,需要li′,ri′∈Z满足以下条件:

(3)

[li′,ri′]∩[lj′,rj′]=∅，i′≠j′.

(4)

对于每一个原始信息区间Di,对应的密文区间为Ci,即通过加密功能使Enc(li)=li′,Enc(ri)=ri′.文中通过划分数据空间来破坏数据分布规律,在Di中包含的数据越多,Ci的范围也就越大.

3.2.3 映射步骤

经过上面2步划分,需要把各个数据映射到密文空间C上,使用加密功能Enc(x)来实现这一目标.对于明文空间中的每个数据x,得到包含x的区间Di=[li,ri],对于不同的区间Di,使用不同的加密功能Enci(x)来把不同的值映射到目标空间Ci=[li′,ri′],总体的过程如下:

(5)

3.2.4 划分方法

划分空间的目标是破坏统计特征,以下将讨论怎么划分明文空间M和密文空间C来实现这个目标.

划分空间的规则如下: ① 若一个原始数据集合存在越多的数据,则应该划分越多的区间,称这些区间作为密集区间; ② 对于一个包含高频数据的原始密集区间Di,其对应的密文空间Ci应该有一个大范围,即对于2个相邻值x1,x2∈Ci,有d(x1,x2)≫1或者|ri′-li′|≫|ri-li|.

上面2个规则能够破坏数据分布,密集区间扩展到密文空间有大的范围,但是稀疏区间扩展到密文空间是小的范围,并且通过这个方法密文会接近均匀分布.

为了实现划分,给出如下参数:

P=(xmin,xmax,{Ti},dmin),

(6)

式中:xmin和xmax为明文的起始点;{Ti}代表密集区间的集合；dmin是文中能设的最小长度的区间.

具体的划分方法如下:令明文空间为

M=R1+T1+R2+T2+…+Rn+Tn+Rn+1，

(7)

式中Rn为稀疏区间,随机选择整数si使区间Ri分成相同的区间,对于密集区间Ti=[li,ri]来说,将其划分为

Ti=dmin+n∩…∩dmin.

(8)

密文空间采用与明文空间相同的划分方法.

数据的更新如下:当在原始数据集合中插入少量新的数据时,密集区间不变;在原始数据集合中插入大量新的数据后,重新对新数据集进行划分密集区间,更改密钥,重新进行加密.

通过上面的划分方法能确定索引数Index(x),表达式为

(9)

3.2.5 加密功能

加密函数Enc()应该满足以下条件:Enc()是可解的,对于∀x∈Di,扩展空间值Enci(x)是很容易通过编程计算的.而且如果yi=Enci(x),那么对应的xi=Enci-1(yi)也应该是可计算的.

可计算的过程:为了实现可编程化,对于第i个区间边界值和x∈Di作为输入,输出结果为y∈Ci.事实上,加密功能函数可以由任何单调递增函数生成.最简单的可计算过程是采用线性方程方法,但是对于重复性数据,采用线性方程方法易于被攻击.所以使用非线性映射来作用在保序加密模型上,且使用的加密函数如下:

Enci(x)=aix3+bi+δi,

(10)

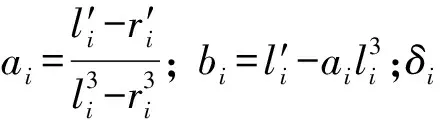
所以加密功能Enc()可以定义为

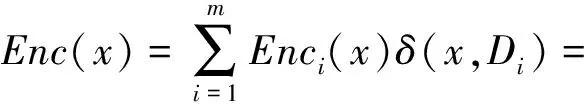
(11)

式中:δ(x,Di)=0，x∉Di;δ(x,Di)=1，x∈Di.

干扰系数δ:这里干扰系数δ可以破坏数据的统计特性.例如,对于高频数据xi,可以构成一对多的映射:

(12)

这是一个点对集的映射,假如使干扰系数δ服从均匀分布,则密文的分布概率是

(13)

因此数据的统计特征可以被干扰系数破坏.

3.2.6 保序加密系统

基于上述划分功能和加密功能,可采用如下的方法来描述文中的保序加密系统:

OPE=(Init,Enc,Dec).

Init()算法在保序加密客户端上执行,需要输入以下参数: ① 明文信息空间M输入空间最小值xmin和最大值xmax; ② 密文空间C输入空间最小值ymin和最大值ymax; ③ 划分明文空间输入密集区间{Ti}和可设置区间最小值dmin; ④ 划分对应密文空间的参数.

最终的密钥k由{li,ri,li′,ri′,dmin}组成.

Enc(x,k)算法在保序加密客户端上执行,来加密数据x输出它的对应密文.为了加密x,首先通过计算Index(x)来得到索引i,然后执行Enci(x)来得到对应的密文.

Dec(y,k)算法在保序加密客户端上执行,来解密数据y输出它的对应明文.可用如下公式表示解密过程:

(14)

在解密之前需要求出包含数据y的密文区间Ci的索引值i.

4 正确性和安全性分析

在上述保序加密系统的前提下,将分析它的正确性和安全性,即抗统计分析和IND-DNCPA.事实上,文中仅存储密文在不信任的数据库上,所以敌手只能得到一些密文而不能得到其他信息.

4.1 算法正确性分析

定理1称保序加密方案nOPE是正确的,如果满足以下条件:

1) ∀m∈D,∃Dec(k,Enc(k,m))=m;

2)x1>x2(x1,x2∈D),有Enc(x1)>Enc(x2).

证明1) 根据该保序加密的结构,每个明文所在的区间是非线性划分的且没有交集,因此保证了任何密文值只能属于一个对应的明文区间.加密时,明文x通过Index函数求出明文所在区间,得到ai和bi,通过aix3+bi+noise来求出密文;解密时,密文y通过Index函数求出密文所在区间,得到ai和bi,来求解出对应的明文.因此,只要加密和解密的过程中使用相同的密钥k,就能使加密的明文解密后得到相同的明文.

2) 该保序加密方案a恒大于0,每个明文加密后的密文没有交集,假设2个相邻的数x1和x2,x1

综上所述,该保序方案是正确的.

4.2 统计攻击

事实上,需要证明文中的基础模型Enc(x)=ax3+b+δ在统计攻击下安全.与统计攻击有关的是相似度的统计,在这种攻击中,攻击者试图基于明文上的一些统计信息找到密文值和明文值之间的匹配,并利用它们来获得密钥.

定理2保序加密方案nOPE是抗统计攻击的.

证明之前的单一映射保序加密,如MIN,MAX和COUNT的统计函数对相同的明文值和密文值是相同的.另外,这种单一映射加密明文值为另一个固定值,所以加密前后数据值的频率是一样的.这种单一映射的保序加密有着高相似度统计Δ,所以这种方案在统计攻击下是不安全的.

文中基本模型中引入了干扰系数δi来阻止统计攻击，映射形式如下:

(15)

式中: |δi|

(16)

本文方案中,因为明文值被加密成许多不同的值,所以明显地明文值和加密后的密文值的频率不同,即

(17)

此外,MIN,MAX和COUNT的统计函数在密文和明文值上完全不同,因此关于明文值的统计量∑p和对于密文值的统计量∑c是不同的.可以明显地看出该算法相似度百分比Δ远小于单值映射的相似度百分比.基于定理2,该方案对于统计攻击是安全的,因为统计的相似度百分比Δ相当小.对于统计函数,这个方案仍是在加密数据上直接使用元函数.例如,MIN值是第1个区间的最小加密值,MAX值是最后一个区间的最大加密值.

4.3 IND-DNCPA安全

引理1假设明文空间|M|=m并且Enc具有保序功能,在选择明文攻击下经过logm次询问可以得到关于任何密文的范围.

所有的保序加密算法在选择明文攻击下面都是不安全的,所以对于选择明文攻击作出限制,称之为IND-DNCPA攻击.

定理3保序加密方案nOPE是IND-DNCPA安全的.

证明由于方案具有保序性,敌手A可能通过分析M中密文的差距以及与m0或m1最近点的密文来推断b.

1) 当A通过求出平均距离

(18)

来猜测x的值时,由于方案是非线性映射y=ax3+b,使得密文与参照函数

f(x)=Enc(x1)+(x-x1)d

(19)

相差很大,因此,A无法从密文直接猜测出相对应的明文.

2) 当A通过分析密文之间的距离d′来推测密文的值域时,当相邻的2个点在同一个区间中时,有

d′=ai(xi+1)3-ai(xi)3;

(20)

当相邻的2个点在不同区间时,有

d′=ai(xi+1)3+bi-aj(xi)3-bj+noisei-noisej

(21)

使得A要判断值域的大小变得很困难.

因此,A的优势概率为

Adv(A)=|pr[b′=b]-0.5|=ε,

(22)

式中ε是一个足够小可忽略不计的数.

综上所述,该算法是具有IND-DNCPA安全的.

5 仿真和实现

5.1 实施细节

对于文中算法,需要保护数据格式并且形成数值型保序加密密文.在实际应用中,数字范围通常不大,而数据库为数值数据提供了一些具有大范围的数据类型,例如,SQL server的“real”型范围是从-3.40×1038到3.40×1038,足够用于一些保序加密的应用程序.通过这种方式,保序加密密文将是实数,并且可以存储在原始字段中,从而导致对现有软件的最小更改.文中方案的所有保序加密操作包括加密和解密操作都是只在客户端上执行.因此,这个可以用任何可编程语言部署和实现,包括java,c++等.本次方案在Win10的试验环境下实现,使用工具为MyEclipse 10和Matlab 7.1.

5.2 试验结果

用一组学生成绩来测试该算法的实际表现,测试其执行时间,显示加密后的数据分布,试验结果如图4-6所示.图4给出了保序加密的平均执行时间.

由图4可见,每10万个加密数平均加密执行时间大约30 ms,而Boldyreva′09算法加密一个数据需要花费176 ms,所以文中保序加密方案执行时间短、效率高.图5给出了试验数据.

图4 加密平均执行时间

图5 试验数据

图5a给出了学生成绩的原始数据分布,可见学生的成绩主要集中在70到90之间.图5b给出了加密后学生成绩的数据分布,对于相同的数据则是加密成为不同的数据,即在区间[ax3+b,ax3+b+noise],具体数据72加密值范围为[17 507 936,17 835 985].图6给出了数据分布.

图6 数据分布

由图6可见,加密后数据分布明显被破坏了.

5.3 方案比较

在效率、安全性和可编程3个方面,把文中方案和其他经典的保序加密方案(Popa′13和Liu′16)进行比较,表1给出了比较结果.

表1 文中方案和其他经典的保序加密方案的比较

由表1可见:

1) 关于效率,Popa′13的方案有最低效率.在Popa′13方案中当加密一个值的时候,客户端需要和服务器相互作用,而且服务器需要在添加和删除节点的时候平衡二叉树,这大大地降低了方案的效率.而文中方案和Liu′16方案使用一些没有交互的非线性数学函数,有着相同的效率,方案的执行时间短、效率高.

2) 关于安全性,Popa′13方案达到了理想安全.相比较Liu′16线性映射方案,文中方案使用非线性映射来隐藏数据分布和数据频率,克服了对于重复型数据线性映射的缺点,它能抗统计攻击和IND-DNCPA,达到更高安全性.文中方法不准备和Popa′13方案一样达到理想安全,因为会失去保序加密对于密文数据直接比较的特点,会限制保序加密的应用,方案中通过隐藏数据分布和数据频率来提高保序加密方案的安全性.

3) 关于可编程性,文中方案有着更好的应用.该方案通过可编程语言易于实现非线性保序加密功能.但是在Popa′13方案中,除了树平衡操作,用户定义功能需要在不同数据库上实现,这增加了可编程难度.

6 结 论

1) 指出在密文数据直接比较时,隐藏数据的分布和数据频率是十分重要的也是保序加密的目标.

2) 在方法中引入干扰系数和扩展消息空间的方法,克服了对于重复型数据破解密钥的问题,使得明文的统计特性被破坏了从而达到了抗统计攻击,并且达到了IND-DNCPA.

3) 通过没有交互的非线性数学函数,方法的效率大大提高.

4) 该保序加密方案不仅有着以前保序加密的优点(即能在不解密密文的前提下在服务器上直接进行范围查询),而且安全性分析和性能评价展示了该算法既安全又高效.

)

[1] BEHERA A, RATHA B K, SETHI S. Green cloud computing: a survey[J]. IJSEAT, 2017, 4(12): 763-767.

[2] RASTOGI N, GLORIA M J K, HENDLER J. Security and privacy of performing data analytics in the cloud: a three-way handshake of technology, policy and management[J]. Journal of Information Policy, 2015, 5:129-154.

[3] 季一木, 朱曈晖, 柴博周,等. 云环境下用户隐私混合加密方案及其性能分析[J]. 重庆邮电大学学报(自然科学版), 2015, 27(5):631-638.

JI Y M, ZHU T H, CHAI B Z, et al. Hybrid encryption scheme and performance analysis for user′s privacy in cloud[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition),2015,27(5):631-638.(in Chinese)

[4] 乔帅庭, 韩文报, 李益发,等. 一种改进的中间域多变量公钥签名方案[J]. 四川大学学报(自然科学版), 2014, 51(3):512-516.

QIAO S T, HAN W B, LI Y F, et al. An improved medium-filed multivariate public key signature scheme[J]. Journal of Sichuan University(Natural Science Edition), 2014, 51(3):512-516.(in Chinese)

[5] 邬海琴,王良民.基于连通支配集的无线传感网top-k查询最优支撑树研究[J].电子学报,2017, 45(1):119-127.

WU H Q, WANG L M. Connected dominating set based support-tree for top-kquery in wireless sensor networks[J]. Acta Electronica Sinica, 2017, 45(1):119-127. (in Chinese)

[6] 刘湘雯, 王良民. 数据发布匿名技术进展[J]. 江苏大学学报(自然科学版), 2016, 37(5):562-571.

LIU X W, WANG L M. Advancement of anonymity technique for data publishing[J]. Journal of Jiangsu University (Natural Science Edition), 2016, 37(5):562-571. (in Chinese)

[7] 宁子岚. 面向云存储基于属性的隐私保护算法[J]. 吉林大学学报(理学版), 2017, 55(4):921-926.

NING Z L. Attribute based privacy preserving algorithm for cloud storage[J]. Journal of Jilin University (Science Edition), 2017, 55(4):921-926.(in Chinese)

[8] AGRAWAL R, KIERNAN J, SRIKANT R, et al. Order preserving encryption for numeric data[C]∥Procee-dings of the 2004 ACM SIGMOD International Confe-rence on Management of Data. New York: ACM, 2004:563-574.

[9] BOLDYREVA A, CHENETTE N, LEE Y, et al. Order-preserving symmetric encryption[C]∥Proceedings of the 28th Annual International Conference on the Theory and Applications of Cryptographic Techniques. Heidelberg: Springer Verlag, 2009: 224-241.

[10] POPA R A, LI F H, ZELDOVICH N. An ideal-security protocol for order-preserving encoding[C]∥Proceedings of the 2013 IEEE Symposium on Security and Privacy. New York: IEEE, 2013:463-477.

[11] KERSCHBAUM F, SCHRÖPFER A. Optimal average-complexity ideal-security order-preserving encryption[C]∥Proceedings of the 21st ACM Conference on Computer and Communications Security. New York: ACM, 2014: 275-286.

[12] MALKIN T, TERANISHI I, YUNG M. Order-preserving encryption secure beyond one-wayness[C]∥Proceedings of the 20th International Conference on the Theory and Application of Cryptology and Information Security. Heidelberg: Springer Verlag, 2014: 42-61.

[13] MAVROFORAKIS C, CHENETTE N, O′NEILL A, et al. Modular order-preserving encryption, revisited[C]∥Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2015: 763-777.

[14] LI K, ZHANG W M, YANG C, et al. Security analysis on one-to-many order preserving encryption based cloud data search[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(9): 1918-1926.

[15] LIU D X, WANG S L. Nonlinear order preserving index for encrypted database query in service cloud environments[J]. Concurrency and Computation: Practice and Experience, 2013, 25(13): 1967-1984.

[16] 黄汝维,桂小林,陈宁江,等.云计算环境中支持关系运算的加密算法[J].软件学报,2015,26(5):1181-1195.

HUANG R W,GUI X L,CHEN N J, et al. Encryption algorithm supporting relational calculations in cloud computing[J]. Journal of Software, 2015, 26(5):1181-1195. (in Chinese)

[17] LIU Z L, CHEN X F, YANG J, et al. New order preserving encryption model for outsourced databases in cloud environments[J]. Journal of Network & Computer Applications, 2016, 59:198-207.