跨越学科的边界,从数学教学走向数学教育
——以“平均数的再认识”教学为例
◇李京华

课堂教学应通过真实的问题情境,鼓励学生在现实挑战中发现知识、学习知识、运用知识,建立新旧知识之间的必然联系。而知识的综合逐渐成为世界科技发展的主导趋势,综合交叉学科已经成了创新的重要来源。通过跨学科、跨领域的方式,构建以解决现实问题为目的的多学科整合学习,弥合分科教学对学生认识知识的割裂,让教育回归自然,让深度学习自然发生。
一、重构单元教学内容,着重培育学生的公民意识
“平均数的再认识”一课是北师大版教材五年级下册“统计与概率”部分的内容。教材中本节课分两大块内容:一是通过讨论1.2米免票线的合理性,体会平均数的代表性;二是通过歌唱比赛打分的情境,让学生体悟有时去掉极值再求平均数,能更好地代表一组数据的平均水平。免票线的情境是现实存在的社会现象,蕴含着丰富的育人功能,能够激发学生的社会参与意识,培养学生的责任感与担当意识,这在数学学习中非常难得!作为一名教育工作者,我们要充分利用教材提供的好情境,尽可能发挥它的教育意义。通过五年的学习,学生已经经历了大量的统计活动,积累了丰富的收集、整理、表示数据的经验及初步分析数据的经验。对平均数的再认识,本课是基于对“身高不足1.2米的儿童免费乘车”这一规定的由来及解释其合理性展开学习的。那么,学生是否愿意讨论此问题呢?我对五年级27名学生进行了调查。
1.你知道在北京身高多少以下的儿童可以免票乘坐公交、地铁吗?
A.不知道 B.知道,身高( )以下的儿童可以免票乘坐公交、地铁
2.你知道我国身高多少以下的儿童可以免票乘坐火车吗?
A.不知道 B.知道,身高( )以下的儿童可以免票乘坐火车
3.你想了解有关免票线的事情吗?简单写写理由。
调查结果统计如下:
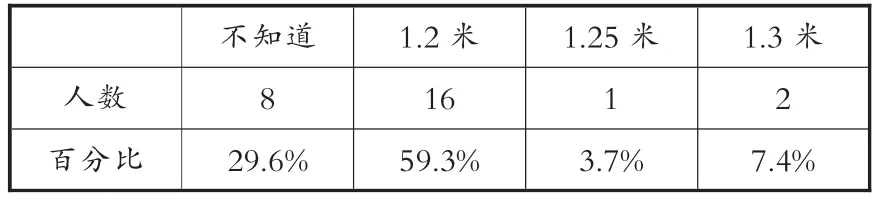
表1 “北京公交、地铁免票线”调查统计表
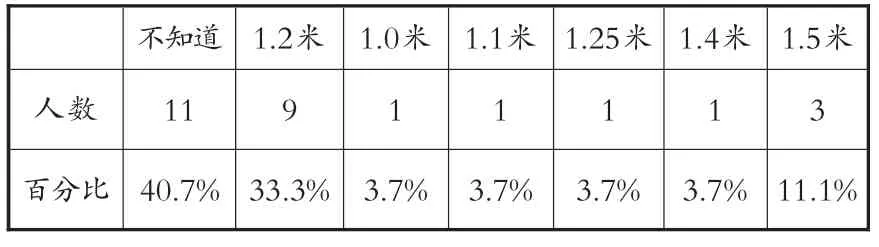
表2 “全国火车免票线”调查统计表
由上面的数据我们可以看出,学生对免票线这一社会事件并不了解,北京公交、地铁免票线是1.3米,正确率只有7.4%;全国火车免票线1.2米,正确率也只有40.7%。而对是否想了解关于免票线的事情,学生的回答更加出乎我们的意料:

表3 “是否想了解有关免票线的事情”调查统计表
面对一个自己刚刚经历过的社会事件,学生了解的正确率如此之低,近一半的学生却选择并不想了解这些事情了,因为已经与其无关。面对学生的回答,我的内心受到了极大的触动!中国学生发展核心素养是以培养“全面发展的人”为核心的,而一个全面发展的人,他的社会参与和自主发展、文化底蕴是同等重要的!我们的数学课,不能仅仅定位在让学生会去掉最高分和最低分再算平均数,我们有义务、有责任让学生意识到自己的责任担当!那么“1.2米免票线是否合理”这一问题,就自然融合了品德与社会的内容。依据对教材以及学生的分析和思考,我们重新构建了“平均数的再认识”单元教学,结构如下:
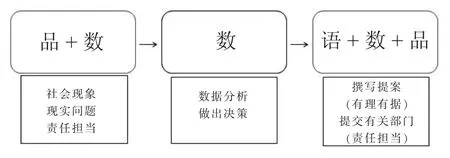
第一课时由思想品德老师和数学老师联合教学,激发学生的责任担当,确定解决“1.2米免票线是否合理”这一问题的流程,讨论收集数据的方法,布置收集数据的作业。
第二课时由数学老师教学,引导学生共同分析数据,做出决策。当然,课上我们讨论的是分析方法。由于数据的局限性,并不能真正得到结论,还需要扩大样本继续研究。因为这次的样本应该是全国范围内的,需要老师、同学甚至家长协同完成。
第三课时由语文、数学和思想品德老师联合教学,借助数学上的分析结果,运用适当的表达方式撰写提案,提交有关部门。
二、应用知识解决问题,培养学生的科学精神
“平均数的再认识”一课承载着培养学生数据分析观念的功能。面对“1.2米免票线是否合理”这一问题情境,学生需要经历调查、收集数据、分析数据、做出决策的全过程。
在解决“1.2米免票线是否合理”这一问题的过程中,学生调查研究的意识,对数据来源、处理、结果进行合理质疑的意识,尊重事实的态度,及用数据说话的习惯都能得到很好的体现,这势必会催生学生实事求是的科学精神。
师:大家都调查了吗?谁来说说你是怎么调查的?调查了几个数据?
生:我调查了4个人,我是问的方式,我问了一些7岁的小学生。
师:我们要调查几岁的?
生:6岁的,但是差不多,我调查的身高是1.27米。
师:他说了一个词“差不多”,大家怎么看?
生:我觉得如果只是差不多的话,数据会不准确,不能作为证据,不适合做一个给国家的提案。
师:应该要什么样的数据呢?
生:准确的。
生:真实的。
教师小结:对,我们要真实准确的数据,没有了这个前提,我们的提案就没有意义了。如果你缺少数据的话,老师也调查了一些,一会儿可以提供给你。
师:想一想这个1.2米的免票线到底合不合理?
生:合理。
生:不合理。
师:说说你的想法和需求?
生:数据还太少。
师:仅仅是数据太少吗?还有没有别的想法?
生:我认为这些都是北京地区的,有些地区人比较高,有些地区人比较矮。
师:是啊,调查数据时还要考虑区域。
师:根据目前的数据你能做提案了吗?
生:不能,需要扩大调查范围,重新调查,再做分析。
三、明晰概念的本质,提升数学素养
1.了解同样的数据可以有多种分析的方法,需要根据问题的背景选择合适的方法。
师:请大家仔细观察自己收集上来的这些数据,是否能解决1.2米免票线合理不合理的问题,说说你的想法。
生1:我调查的是6岁儿童的身高,可以求出平均数看合不合适。
生2∶我调查的身高可能比较凑巧,数据都很高,全都超了,一看这些数据就觉得1.2米免票线不太合理,最矮的是1.28米。
生3∶我调查了10个人,其中6个人可以享受这个免票待遇,按比例就是6∶4,所以我觉得1.2米免票线还是合理的。
生4:我想选一个范围,到街上调查一些行人,问问1.2米免票线是否合理,然后做出判断。
生5:可以像比赛那样,评分时几个评委一起打分,去掉一个最高分和一个最低分,剩下的再求平均数。
师:面对这么多的方法,你有什么想法?还有什么问题?四人小组讨论讨论。
组1:我觉得生5的方法比较可行,因为最低的和最高的差太多了,应该去掉最低和最高的再求平均值。
师:为什么想到去掉最高的和最低的呢?
组1:如果不去掉最低的和最高的身高,这个身高可能到另一个年龄段了。
师:你认为它(极端数据)对平均数产生了干扰。
生1:我想对他们的结论进行反驳,全北京的儿童有这么多,你怎么知道你去掉的是最高的身高呢?可能有极端的1.35米和1.34米,你把1.35米去掉有什么意义呢?
生1:我觉得数一数谁最多比较好,大部分人都超过了1.3米就要改,大部分人都没超过就不用改了。
生2:我想给他一点补充,他这样想应该是将这个免票线设在最普遍的群体上。
师:你觉得这个免票线应该代表大多数人。
生3:我觉得每个人的数据在一定程度上都是不太准确的,如果你找到的都是一点三几米的数据,你是不能这么武断地说1.2米的免票线是不合理的。也有可能你找了好多是那种特别矮的,超过1.2米的人非常少,也不能说1.2米是合理的。
师:简单说一下你的观点。
生3:我觉得应该取平均数,而且要取多数人的平均数,数据要尽量的多,这样才能保证越接近实际情况。
2.在运用平均数解决问题的过程中,发现平均数很灵敏。
在数据较少时,平均数受极端数据影响较大。在对极端数据处理方法讨论的过程中,学生逐步意识到当数据足够多时,极值对平均数的影响就不那么明显了,加深了学生对平均数的再认识。
师:在刚才的讨论中,大多数同学选择了平均数。接下来就按你们说的,扩大点儿数据,两人一组,借助平板电脑算一算收集到的6岁儿童的平均身高。思考:平均数是否能代表你们组身高数据的整体水平,帮我们做出判断?
生:我把我们得到的数据输入平板电脑,发现平均数是121.6厘米,比120厘米大,我们还发现大部分数据都大于120厘米,所以我们认为120厘米的免票线不合理。
师:看了他们的这组数据,你们有什么问题吗?
生:我觉得138厘米这个数据不太合理,好像太高了。(如图1)
生:我觉得也有可能有138厘米身高的,比较特殊罢了。
图1
师:那么,121.6厘米能不能代表这一组数据的总体水平呢?
生:我还是建议去掉138厘米再算平均数,因为138厘米太高了。
师:去掉这个极端数据,再算一下平均数。
生:平均数变成120.429厘米了。
师:让我们动态看一下去掉138厘米前后的变化,思考该不该去掉呢?
生:我觉得应该去掉,去掉后平均数依然大于1.2米,所以我认为免票线不合理。
生:我觉得去不去掉都可以,因为多数人还是高于1.2米。
师:有人认为应该去掉,有人不认同,这个问题我们暂时存在这里。
师:还有哪组愿意说一些你们的数据?
生:我们合起来的数据共有30个,平均身高是114.821厘米,不超过1.2米,在这30个数据中,只有三四个超过了1.2米,我觉得1.2米免票线是比较合理的。
生:我们组调查的人的平均身高是123厘米,只有4个人的身高没有超过1.2米,其他都超过了。(如图2)
图2
师∶大家观察一下这组平均数在发生变化,有什么变化呢?(如图3)

图3
生:我发现不管加不加后边的数据,平均数都在1.2米旁边游荡,低于1.2米的很少,一般都比1.2米高一点。
师:你的意思是当数据足够多时平均数就在一个数值左右徘徊,趋于稳定,就能够代表大多数人的身高水平。跟我们最开始的初衷是否一致?
生:我觉得并不是因为他们的身高都在1.2米左右,而是因为加上的数越来越多时,平均数的变化就比较小了,数多了比较可靠。
师:现在我把这些数据一个一个删除,再按回车键看一下平均数动态的变化过程。思考:这个平均数敏感吗?稳定吗?
生:它稳定保持在一个阶段,摆动不是特别大,敏感的是只要加一个数它就会变化,就算是很小很小的数,它也会变化。
师:说明每个数都有它的意义、价值和影响。师:在什么情况下稳定呢?
生:在人多时。
师:当数据多了,它就稳定在一个值的左右,就能代表这组数据的平均水平了。
师:我们再看之前的138厘米,要不要去掉呢?
生:不能去掉,因为刚才讨论过了,每个数都有它的意义。
生:当数据足够多时影响就小了,就不用去掉了。
总之,“平均数的再认识”这节课,始终围绕着“1.2米免票线是否合理”这一现实问题展开讨论,在解决这个问题的过程中,学生自然而然地想到要调查、收集数据、分析数据、做出决策,从而解决问题。在解决问题的过程中,鼓励学生亲近数据,愿意用数据说话,能从数据中提取一些信息,而在用数据的过程中,自然想到平均数,在对极端数据处理方法的讨论中,深入理解平均数的代表性,感受平均数的价值,数据分析观念和应用意识自然而然地融入学生的思维中,落实了对数据分析观念及应用意识的培养。

