空间刚柔耦合并联机器人动力学求解策略

刘 凉 赵新华 周海波 王嘉斌

(天津理工大学天津市先进机电系统设计与智能控制重点实验室， 天津 300384)

0 引言

柔性多体系统由于建模复杂和求解困难一直是动力学领域研究的热点[1-5]。在建模方法上，运动弹性动力学法的模型简单，但忽略了大范围刚体运动与弹性变形之间的耦合特性，仅将二者进行线性叠加，故无法对弹性体大变形进行精确描述[6-8]。浮动坐标系法将构件的弹性变形与大范围刚体运动构建为零次耦合模型，适用于描述小变形的场合，由于刚柔耦合项的存在，使复杂柔性机构的求解变得十分困难[9-11]。SHABANA等[12-14]提出了绝对节点坐标法，它使用绝对位置坐标及其变形梯度作为柔性体单元的节点坐标，可直接描述柔性体大范围刚体运动和大弹性变形以及二者的非线性耦合特性，但复杂的应变能形式降低了动力系统的求解效率。虽可通过引入稀疏不变矩阵加以改善[15]，但求解时应规避泊松闭锁问题。

通常隐式积分法在求解多体系统的刚性微分方程时更为有效[16]。HUSSEIN等[17]将隐式HHT-I3法与显式ADAMS法作了比较；由于Generalized-α数值迭代法可对高频模态实现可控的人工耗散[18-19]，求解效率较高。目前，非因果解仍然是评判柔性系统逆动力学解特性的重要标准，因为它能求出唯一有界解[20]。但该方法不适于具有高度非线性弹性力项的动力系统，应构建合理的求解方法来寻求多体系统高效稳定的数值因果解，同时还应考虑约束条件下动力系统的相容性问题。本文研究3-RRRU空间刚柔耦合并联机器人动力学模型稳定因果解的求解策略。

1 刚性构件与柔性构件的质量矩阵

由于空间3-RRRU并联机构中含有刚性梁单元、刚性三角动平台和柔性梁单元，所以应先分别求出其质量矩阵以便构建系统的动力学方程。

1.1 空间刚性梁单元的质量矩阵

图1基于自然坐标法描述了一种各向同性、质量分布均匀且横截面一致的空间刚性梁单元。梁的中性线上任意一点的绝对位置矢量可表示为

ri(x)=rji+x(rj+1i-rji)/|rj+1i-rji|=Srqi

(1)

其中

(2)

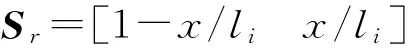
(3)

式中Sr——刚性梁的形函数，Sr∈R3×6

qi——刚性梁的自然坐标矢量，qi∈R6

⊗——克罗内科张量积

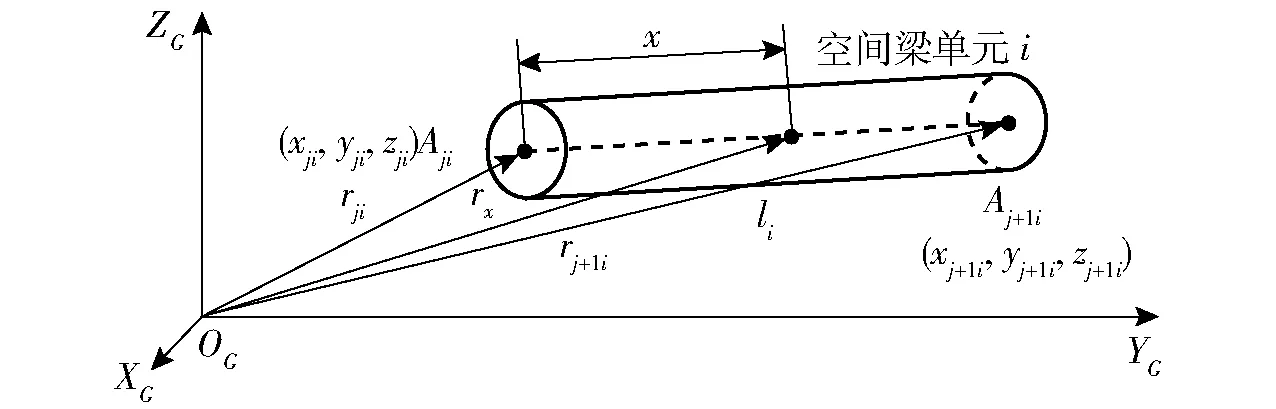
图1 NCF法描述的空间刚性梁单元模型Fig.1 Spatial rigid beam described in NCF

根据惯性力的虚功率计算公式[20]，刚性梁单元的质量矩阵可表示为

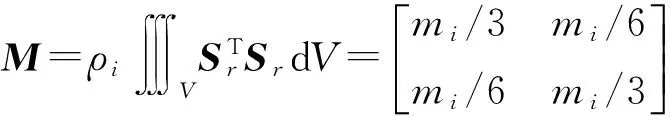
(4)

式中ρi、mi——刚性梁密度、质量

显然，式(4)描述的质量矩阵为对称的常数矩阵。

1.2 刚性三角形平台的质量矩阵

一种基于自然坐标法描述的各向同性、质量分布均匀且厚度一致的空间正三角形平台如图2所示，其外接圆的半径为r。为求其质量矩阵，引入两个空间基点A41与A42以及在局部坐标系oxyz下描述的两个单位矢量u和v。这两个基点亦可在局部系下分别用矢量ri和rj来描述。三角形平台上任意一点在全局坐标系下的度量为[20]

r=Cqa

(5)

式中C——三角平台形函数，C∈R3×12

qa——三角平台自然坐标矢量，qa∈R12

由惯性力的虚功率可得出该平台的质量矩阵

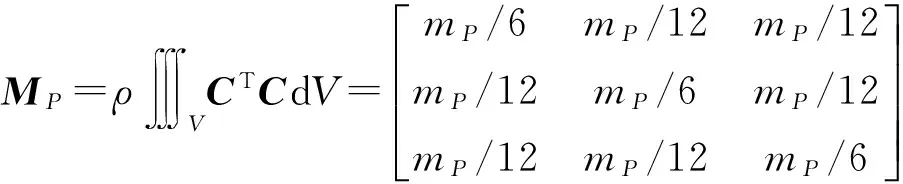
(6)

式中ρ、mP——三角形平台密度、质量

该质量矩阵为对称的常数矩阵。对应的自然坐标矢量为

(7)

式中xi、yi、zi(i=3,6,9)——平台顶点的自然坐标

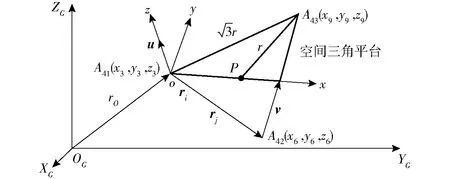
图2 NCF法描述的空间刚性三角形平台模型Fig.2 Spatial rigid triangular platform described in NCF

1.3 空间柔性梁单元的质量矩阵

利用绝对节点坐标法[12]，可求出各向同性、质量分布均匀且横截面一致的空间柔性梁单元的质量矩阵

Mij=∭VijρijSijTSijdVij

(8)

式中ρij、Vij——柔性梁密度、体积

Sij——柔性梁单元形函数

柔性梁单元的质量矩阵为对称的常数矩阵，该单元的节点坐标矢量eij为

(9)

式中m、n——梁单元的首端点、末端点

rijm、rijn——首末端点处绝对位置矢量

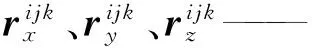
2 刚柔耦合并联机器人的动力学方程

2.1 3-RRRU刚柔耦合并联机器人

3-RRRU并联机器人如图3所示，它由静平台、动平台及3条结构对称的支链组成，其中静平台和动平台为等边三角形，各支链包含3个运动杆件(前2个杆件为刚性杆，最后1个杆件为柔性杆)、3个转动副和1个虎克铰。所有运动关节都是刚性关节，与静平台相连的转动副为驱动副。图4给出了利用自然坐标法和绝对节点坐标法构建动力学方程时各个杆件广义坐标的定义方式。

图3 3-RRRU刚柔耦合并联机器人Fig.3 3-RRRU rigid-flexible parallel manipulator1.静平台 2.刚性杆 3.柔性杆 4.动平台 5.虎克铰 6.转动关节 7.驱动关节

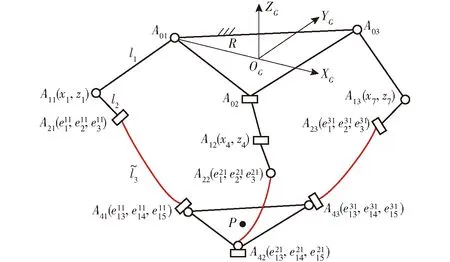
图4 并联机器人的广义坐标Fig.4 Generalized coordinates of parallel mechanism

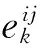
2.2 并联机器人正动力学模型

根据能量原理和前述的刚性、柔性构件的质量矩阵可求出系统的拉格朗日动力学方程，由于此时驱动杆件的动力学参数是已知的，因此该机构在约束条件下的正动力学模型为

(10)

其中，系统的广义坐标矢量可表示为

(11)

式中M——系统的常质量矩阵

Qg——广义重力矢量

Q′——广义驱动力矩矢量

Qe——广义弹性力矢量

Φ——系统约束方程

Φq——系统约束方程的雅可比矩阵

λ——拉格朗日乘子矢量

q——系统的广义坐标矢量

为了便于求解，广义坐标矢量中包含了A11、A12和A13处已知的自然坐标xi和zi(i=1，4，7)。

由于正动力学模型在系统约束条件下进行求解，因此，首先列出第1支链的几何约束方程

(12)

式(12)中，前2个约束方程描述了2个刚性杆的长度约束；第3个约束方程表明第2个刚性杆只做平面运动；其他方程则是对刚性转动关节和刚性虎克铰进行约束。同理，另2条支链亦可列写12个约束方程。最后，刚性动平台的约束方程为

(13)

因此，正动力学模型的全部约束方程为21个。

2.3 并联机器人逆动力学模型

并联机器人逆动力学模型与式(10)具有相同的形式，但是由于各支链的驱动力矩τ1、τ2和τ3均为未知量，故需要添加3个新的约束方程才能进行求解。约束条件下的逆动力学模型为

(14)

式中ΦT——新添加的3个约束方程

(15)

式中xp、yp、zp——动平台中心点P处运动轨迹

由于其他约束方程与正动力学模型中的完全相同，故逆动力学模型的全部约束方程为24个。

3 刚柔耦合动力学系统的求解策略

3.1 动力学方程的数值积分法与相容性问题

由于描述系统动力学模型的微分方程具有刚性特性，所以利用Generalized-α法对高频分量实现可控的数值耗散能准确地求出系统方程的数值解。作为一种隐式数值积分法，在迭代求解时应将系统正、逆动力学方程分别改写为

(16)

(17)

为保证动力学模型的数值解满足系统的求解精度要求，应对式(10)和式(14)中的动力学方程和约束方程的误差函数进行定义。其中，正动力学方程和约束方程的误差函数分别定义为

(18)

(19)

对于逆动力学系统，其约束方程的误差函数还需在式(19)中添加由ΦT描述的3个约束方程。由于误差函数采用了平方和的根式形式，所以对一个给定的误差预设值，能够保证任意一个迭代方程的计算误差都小于该预设值。为了综合考虑该动力系统的迭代误差，将动力学方程和约束方程的误差函数之和定义为该系统的误差函数。

利用上述方法迭代求解时，初始阶段动力学方程的收敛速度比较快，系统误差明显下降，但由于系统方程具有刚性特性，该误差的下降幅度会逐渐减小。随着迭代过程的不断深入，系统误差不会进一步降低反而会不断升高，产生这一现象的原因是系统约束方程的迭代误差正在不断增加，这说明动力学方程在求解过程中与几何约束方程所保持的相容性原则被破坏。而出现该问题的根源在于系统中刚性构件与柔性构件的运动状态是在不同时间尺度下变化的，但二者却混合在一起进行积分，造成了描述刚性构件运动的自然坐标与描述柔性构件运动的绝对节点坐标在迭代时的更新速率不同，从而破坏了系统动力学方程与约束方程的相容性。

为解决该问题，提出一种瞬态刚体校正法，它的基本思想是：在迭代求解过程中，将当前已产生变形的并联机构视为一个刚性机构，倘若此时相容性原则被破坏，则必须在该瞬时状态对该刚性机构的运动学模型进行重构求解，由于此刻的运动学模型与刚柔耦合动力系统的约束方程相容，同时能保持柔性杆的变形状态与弹性力不变，所以该校正法提供的辅助搜索路径或迭代路径能够保持动力学方程与几何约束方程的相容性。此时可利用自然坐标法描述各个构件的瞬时运动状态，即先将图4中A2i(i=1，2，3)点处的绝对节点坐标依次改为自然坐标(x2,y2,z2)、(x5,y5,z5)和(x8,y8,z8)；然后再将A4i(i=1,2,3)点处的绝对节点坐标依次改为自然坐标(x3,y3,z3)、(x6,y6,z6)和(x9,y9,z9)。

3.2 正动力学瞬态刚体校正法

由于已知驱动杆件的运动状态，故只需对其他刚性构件和被视为刚性构件的柔性杆的运动状态进行校正，第1支链的瞬时几何约束方程为

(20)

其中，前2个方程约束了第2杆和第3杆的端点长度；第3个方程是柔性杆上A41点到一个给定平面的距离约束(距离为d1)，该平面通过A21点并与第2转动副的轴线相垂直；最后一个方程约束了虎克铰2个转动副的轴线，其中u3x、u3y和u3z为虎克铰第1转动副轴线的全局坐标。同理，可列出其他2个支链的8个瞬时几何约束方程。最后，三角形刚性动平台的瞬时几何约束方程为

(21)

正动力学瞬态刚体校正法是综合利用这15个约束方程来重构该瞬时刚性机构的运动学模型。

3.3 逆动力学瞬态刚体校正法

此时已知末端执行器的运动状态，需要校正各支链构件及动平台的运动状态，第1支链的5个瞬时几何约束方程包含式(20)和以下约束方程

(22)

以上方程约束了驱动杆的长度；同理，可列出其他2支链的10个瞬时几何约束方程。最后三角形刚性动平台的6个瞬时几何约束方程包含式(21)和以下约束方程

(23)

逆动力学瞬态刚体校正法是综合利用这21个约束方程来重构该瞬时刚性机构的运动学模型。

3.4 刚柔耦合并联机机器人的动力学求解策略

为了获得刚柔耦合系统稳定的数值因果解，除了要满足相容性条件外，还应该从系统能量、求解稳定性、初值点的选取等角度来评价和筛选动力系统的数值解，求解原则如下：

(1)从理论上讲，约束条件下动力学方程的解有无穷多组，故在求解过程中应寻求一组能量最优解。若其解析形式难以求出，则求解方法必须有能力对解集进行筛选，并最大限度地减少系统耗能，来降低残余能量在非采样点处引起的振动。

(2) 求解方法应保证各个采样点处动力学参数的解具有良好的平滑性与一致性，在降低系统耗能的前提下，根据具体运动情况将其变化率控制在合理的范围内，来保证系统能量输出的可持续性与稳定性，避免出现大幅度的能量波动现象。

(3) 由于动力学模型存在刚性特性，为了提高求解效率和计算精度，应对运动起始点的初始状态(初值点)单独进行迭代求解。若初值点为静止状态，则应根据系统的动力学模型推导出相应的静力学方程，并对其进行迭代求解。

(4) 在求解过程中，针对动力学方程与约束方程之间存在的相容性问题，应合理高效地寻求与之相容的迭代路径搜索方法，不断降低系统的迭代误差，避免求解失败。

(5) 大变形柔性构件的建模缺陷会导致在求解过程中出现泊松闭锁问题[21]，可采用缩减积分法解决该问题。另一种方法是建模时使用新型柔性梁单元模型[22]，来彻底规避该闭锁问题的发生。

4 求解实例与实验分析

刚柔耦合3-RRRU并联机器人的仿真物理参数如表1所示。其静平台和动平台的外接圆半径分别为0.175 m和0.06 m。各柔性杆的杨氏弹性模量E为6.9×108Pa，泊松比ν为0.3，截面为圆形，截面半径为0.01 m。各杆件的质量分布均匀。

表1 3-RRRU并联机器人的仿真物理参数Tab.1 Physical parameters of 3-RRRU parallel robot

4.1 正动力学模型求解实例

正动力学模型在求解时需要已知驱动杆的运动状态，为此先按照一个给定轨迹求出理想的全刚性3-RRRU并联机器人驱动杆的运动状态，然后将其作为当前刚柔耦合并联机器人正动力学模型的已知量，来求解末端执行器的运动状态。为验证求解策略的可行性，将末端执行器运动轨迹设为平面ZG=-0.8 m上半径为0.1 m的一个标准圆周，其额定运动速度设为0.5 m/s。为使运动轨迹更平滑，这里引入S-型加减速机制。在求解过程中，将动力学方程和约束方程的误差函数阈值分别设为10-6和10-8。图5为已知的刚性并联机构的驱动力矩，此时求出的末端执行器实际运动轨迹及其与理想圆周的位置误差如图6所示；动平台法向量与全局坐标系ZG轴的夹角如图7所示。

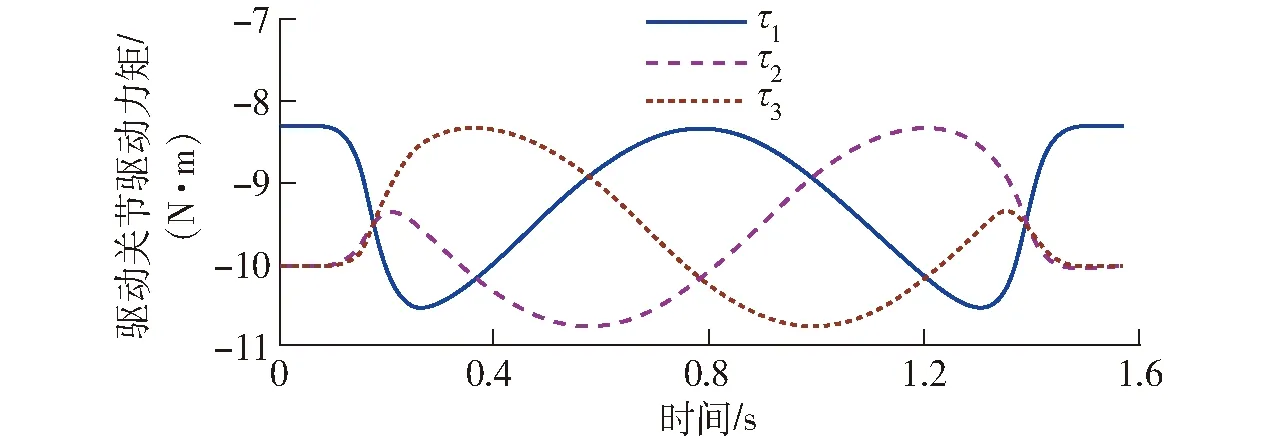
图5 正动力学模型的输入驱动力矩Fig.5 Actuated torques of each limb for forward dynamics

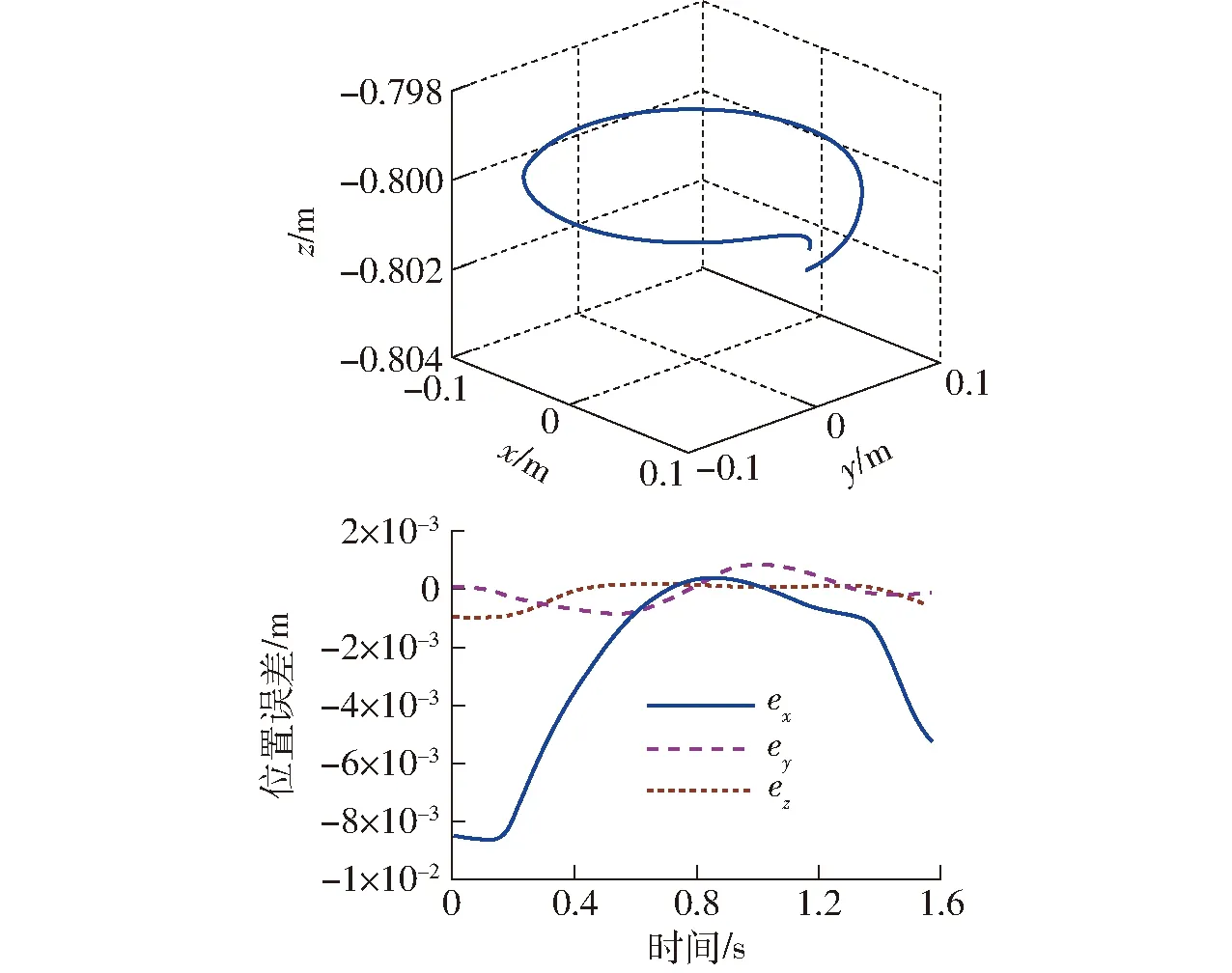
图6 末端执行器的空间运动轨迹和位置误差Fig.6 Spatial trajectory and errors of end-effector

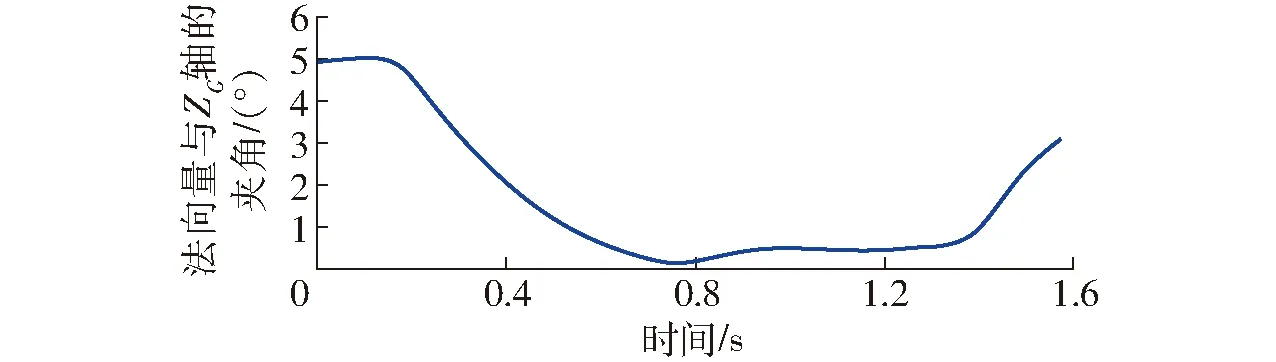
图7 动平台法向量与ZG轴的夹角Fig.7 Angle between platform normal vector and ZG-axis

从上述结果可知，末端执行器的运动轨迹不是标准圆周，在x轴方向的轨迹偏差最大，其最大值为8.7×10-3m，而其余2个方向的偏差均低于2×10-3m，这与坐标系的摆放位置和机构的空间位姿有关。由于柔性杆的变形使得动平台无法保持平动状态。所以根据刚性模型的逆动力学解对刚柔耦合机构实施控制无法得到令人满意的效果。

各支链柔性杆中心点处的横向变形[12]与剪切角如图8所示。二者均呈现出非线性的变化趋势，其中前者的变化过程不具有周期对称性；而后者的幅值比较小，其原因是柔性杆的纵向尺寸远大于其横向尺寸，这符合Euler-Bernoulli梁的假设。图9记录了约束方程和动力学方程的误差函数值，它们均满足系统求解前预设的误差阈值。这验证了正动力学瞬态刚体校正法的可行性和有效性。

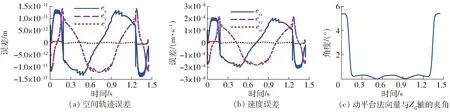
图10 末端执行器的运动状态Fig.10 States of end-effector

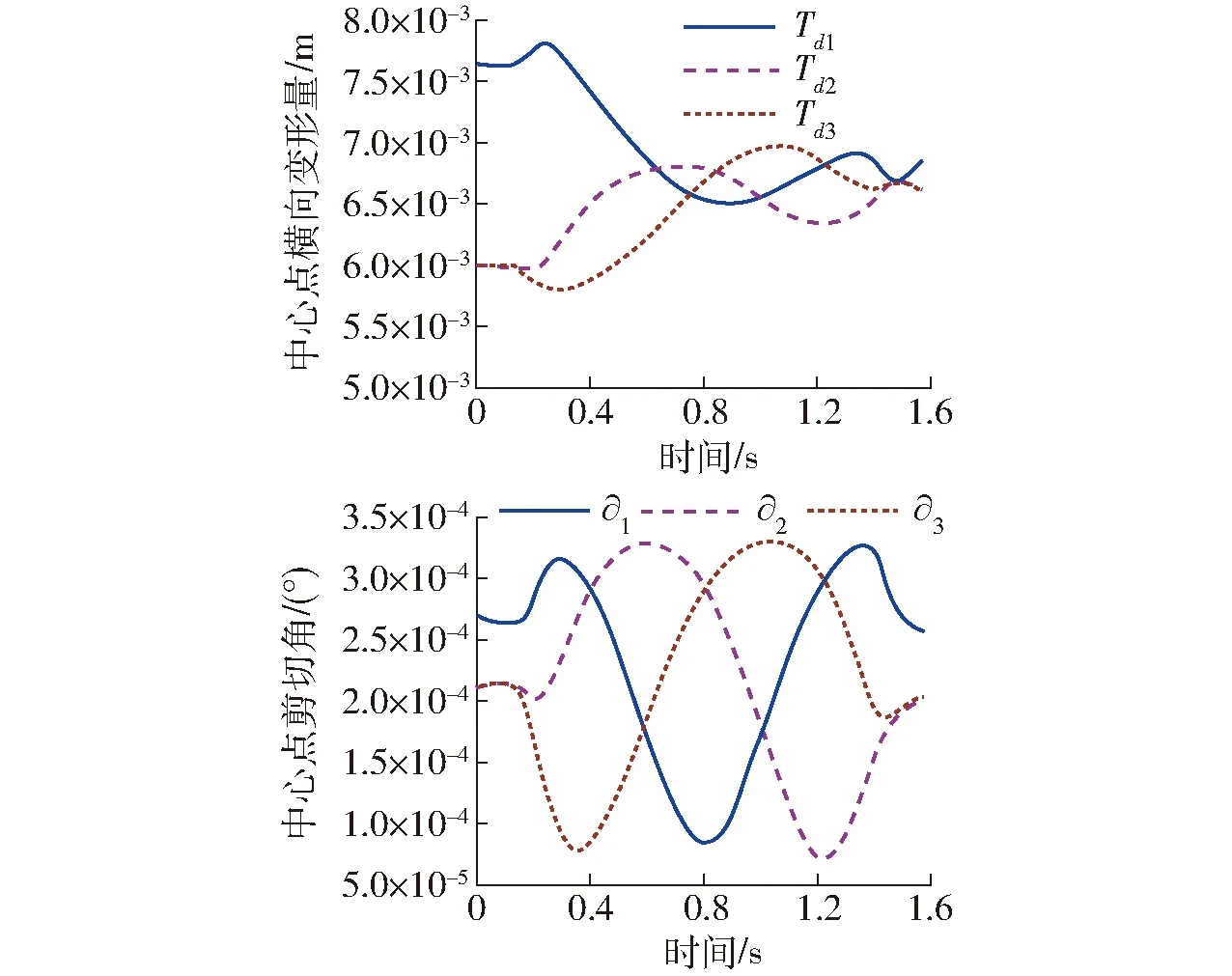
图8 柔性杆中心点的横向变形和剪切角Fig.8 Transverse deformation and shear angles of midpoints of flexible links

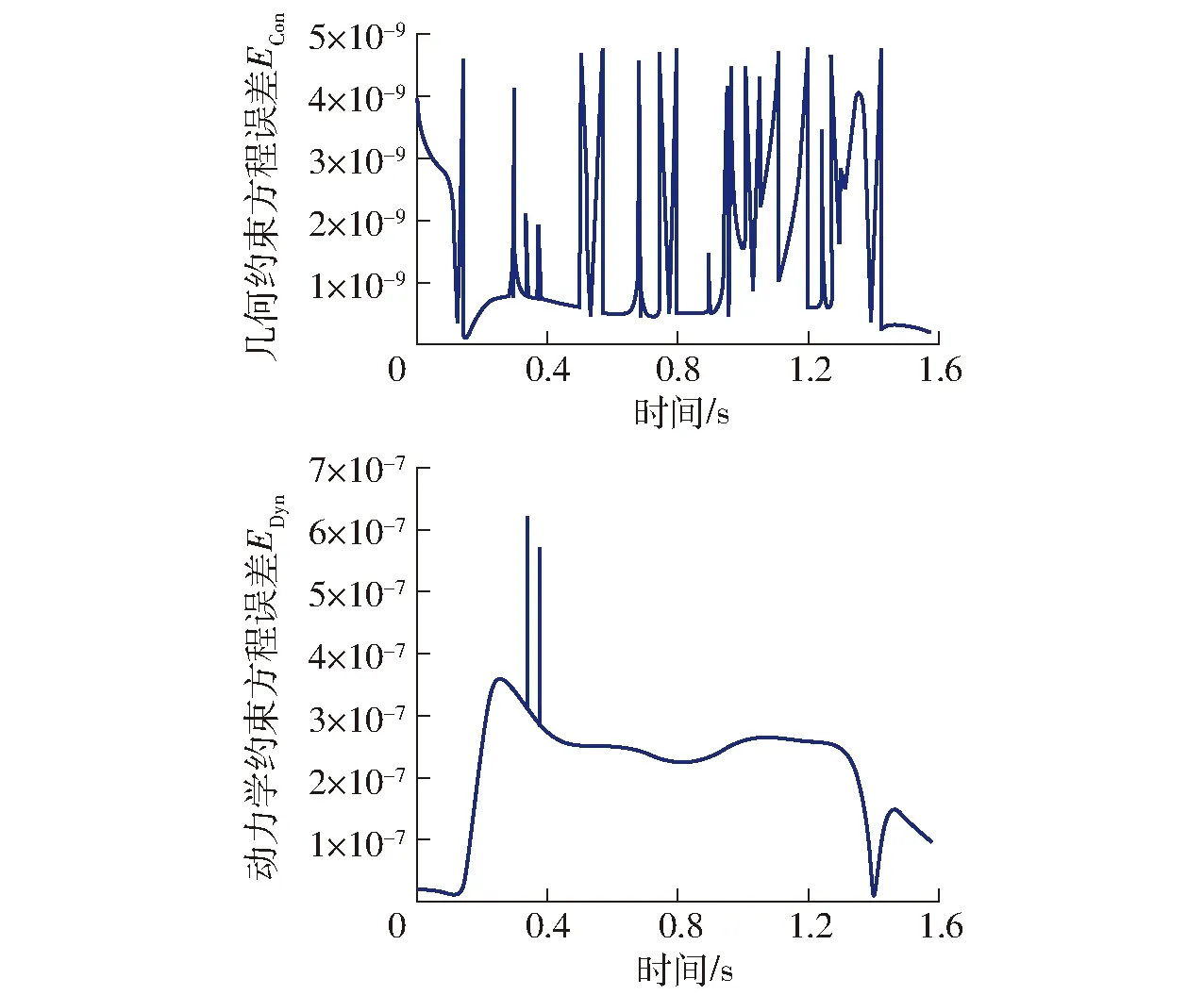
图9 迭代求解过程中约束方程误差和动力学方程误差Fig.9 Iterative errors of constraint and dynamic equations

4.2 逆动力学模型求解实例

依然采用正动力学中末端执行器的规划轨迹和规划速度，根据求解策略求出驱动构件和柔性杆的运动状态，通过引入S型加减速机制来适当缩短系统的加减速过程。图10a、10b给出了末端执行器运动状态的迭代求解值与理想值的误差，其中运动轨迹和速度与理想值都十分接近，二者的误差分别低于2×10-11m和3×10-8m/s，这满足大多数理论分析与工程应用的要求。其次，图10c中给出的动平台法向量与ZG轴的夹角呈现出周期性的变化规律，其最大值为5.3°，出现在起止位置处；匀速运动段中该夹角低于0.5°，而且变化过程平稳，无大幅度振动的现象发生，这说明所求的逆动力学解能通过控制驱动杆的运动状态实现刚柔耦合机器人平稳的轨迹跟踪控制。

此时驱动力矩和驱动角位移如图11a、11c所示，由于动平台不再保持平动状态，所以各驱动力矩之间以及角位移之间的对称性已被完全破坏。其中，驱动力矩最大值出现在第2支链为-11.1 N·m，最小值出现在第1支链为-8.3 N·m；驱动角位移的正向最大值出现在第1支链为9.8°。图11b、11d将驱动力矩和驱动角位移与理想刚性模型的对应值进行了比较，其偏差呈现出非线性的变化特征，其中第2支链驱动力矩的偏差值最大为-0.39 N·m；而第1支链的角度偏差最大为0.84°。各柔性杆中心点处横向变形与剪切角如图11e、11f所示，二者均呈现出非常规范的周期性变化规律，其中第1支链柔性杆的横向变形量最大为7.73 mm；而剪切角均小于0.000 4°，符合细长梁的假设。从以上分析可知，基于逆动力学解的控制方法是通过控制驱动杆的关节变量来合理地控制弹性杆的变形状态，从而保证末端执行器准确平稳地按照理想圆周轨迹进行运动。

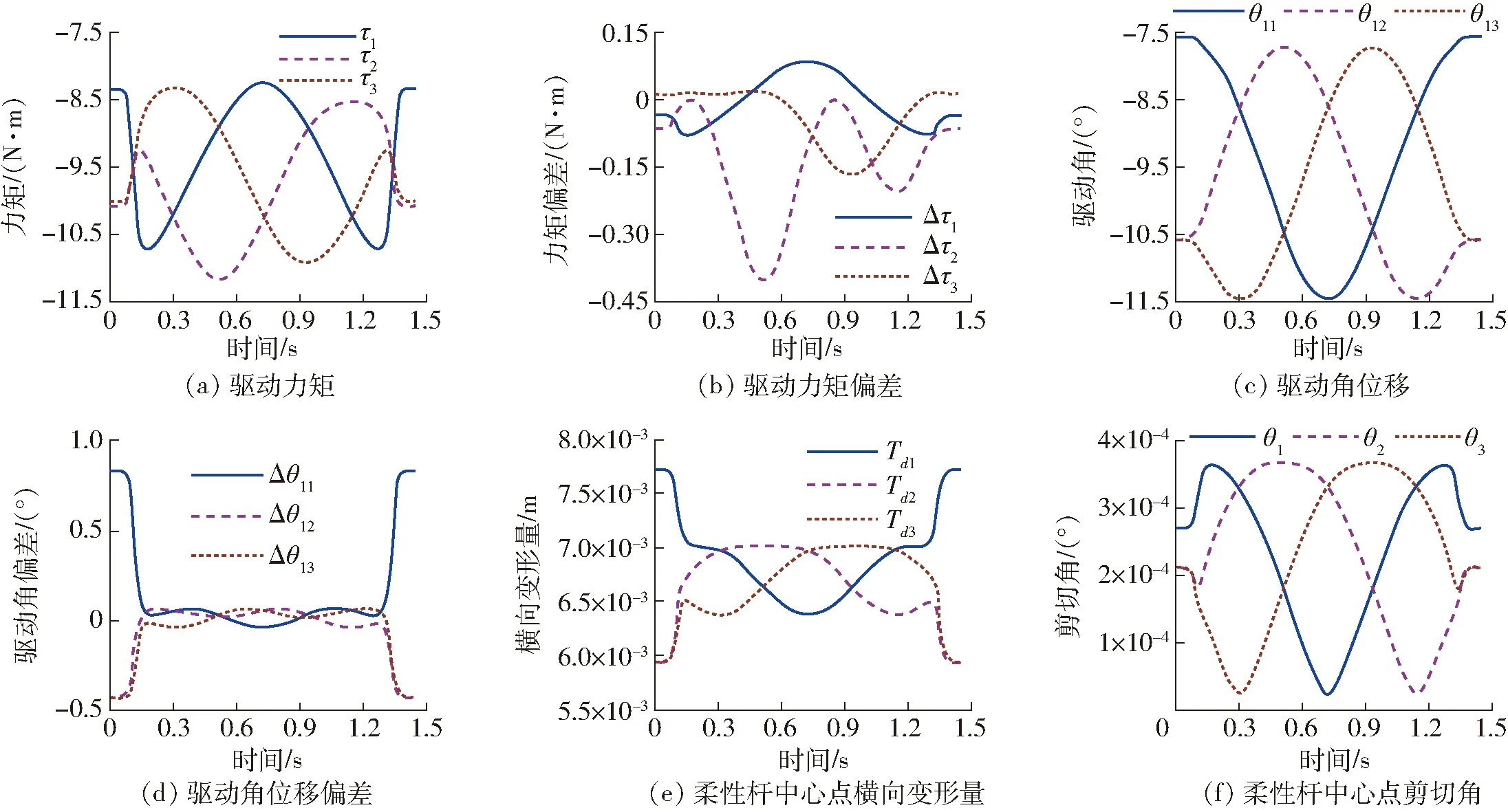
图11 驱动杆与柔性杆的运动状态Fig.11 States of actuated links and flexible links

约束方程和动力学方程的误差函数值如图12所示，二者均低于预设值10-8和10-6，这也充分验证了逆动力学瞬态刚体校正法的有效性。

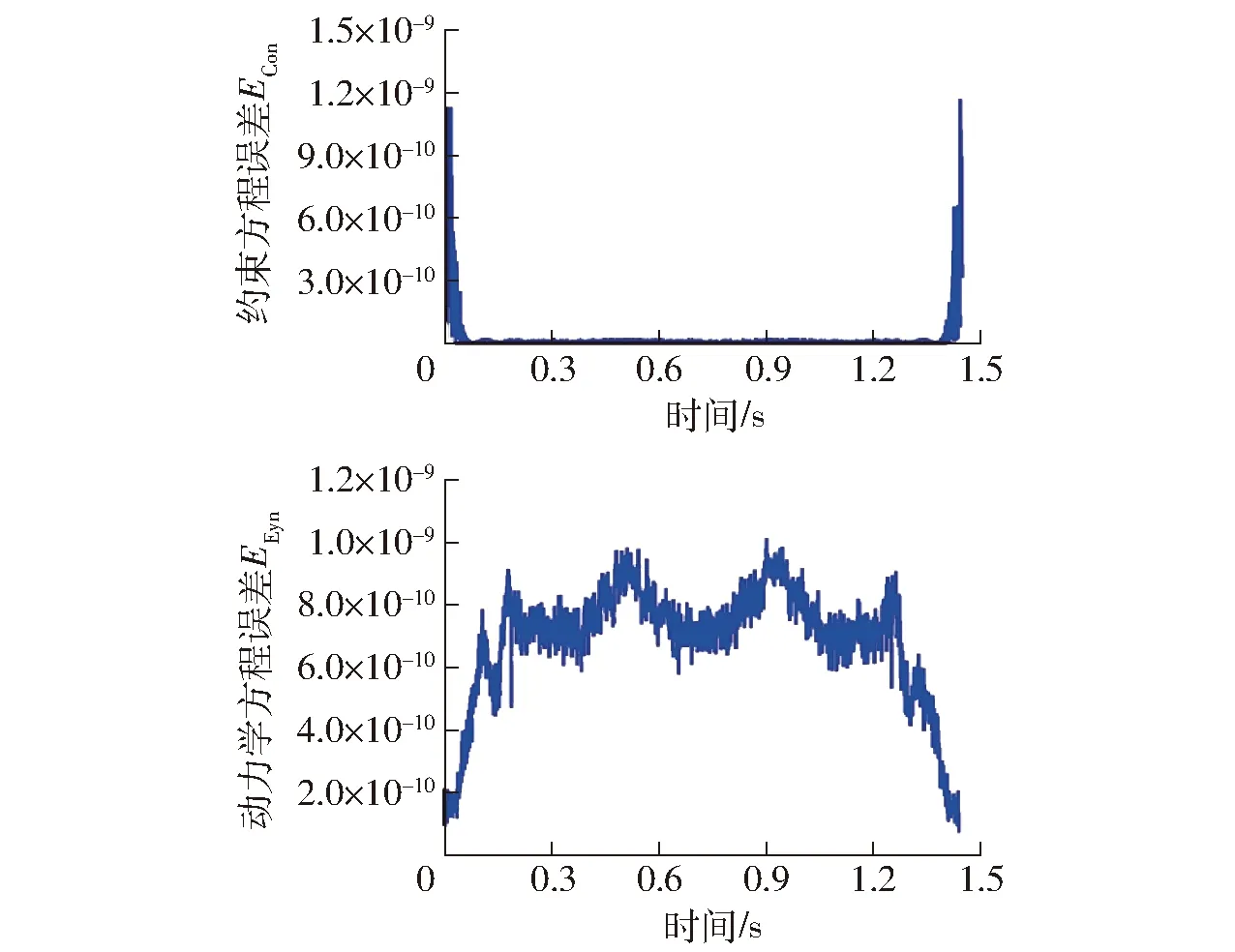
图12 约束方程与动力学方程的迭代误差Fig.12 Iterative errors of constraint and dynamic equations

4.3 运动控制实验

为验证求解策略的有效性，所搭建的实验平台包含刚柔耦合3-RRRU并联机器人，其柔性杆的弹性模量为6.9×1010Pa，其他参数与计算实例中相同；驱动关节通过高精密减速器由交流伺服电机驱动，并采用绝对位置编码器提供关节角度，分辨率为0.005 5°；多轴运动控制器采用Power PMAC，插补周期221 μs；测量设备采用FARO型激光跟踪仪，重复定位精度为0.02 mm。实验前首先要对系统中的机械设备、电控设备和测量设备进行调试和标定。然后，将逆动力学模型的稳定因果解输入给控制器进行轨迹跟踪控制。利用激光跟踪仪对测量靶标的圆心点进行定位，实时记录末端执行器的空间运动轨迹，如图13所示。由于定位靶标的接触面为球面，其圆心到末端执行器的垂直距离为25 mm，因此，实际测量的空间轨迹与末端执行器的运动轨迹会存在偏差。

图13 激光跟踪仪测量系统Fig.13 Laser tracker measuring system

实验包含两部分：令动平台承载1.6 kg负载，首先，根据逆动力学求解策略研究求解实例中圆周轨迹的跟踪性能；其次，测量柔性杆上特征点的轴向主应变，并与理论值作比较。为便于对比分析，实验过程中将分别基于理想刚性模型和刚柔耦合模型的逆动力学解来控制机器人，通过测量末端执行器的空间位置、轨迹精度以及柔性杆上特征点的应变值，来验证求解策略的有效性。

在研究轨迹跟踪性能时，利用激光跟踪仪分别测量两种模型下的圆周轨迹，如图14所示。图中圆弧上引出的直线段表示运动轨迹与拟合圆之间的误差，其长度代表拟合误差的幅值。由表2的测量结果可知，二者在拟合直径上的差距为0.153 mm，但后者的圆度误差降低了1.46 mm，轨迹最大误差降低了0.372 mm，最小误差降低了0.029 mm。从以上对比可知，基于刚柔混合动力学模型的控制效果优于基于理想刚性模型的控制效果。这进一步验证了所述控制方法的有效性。

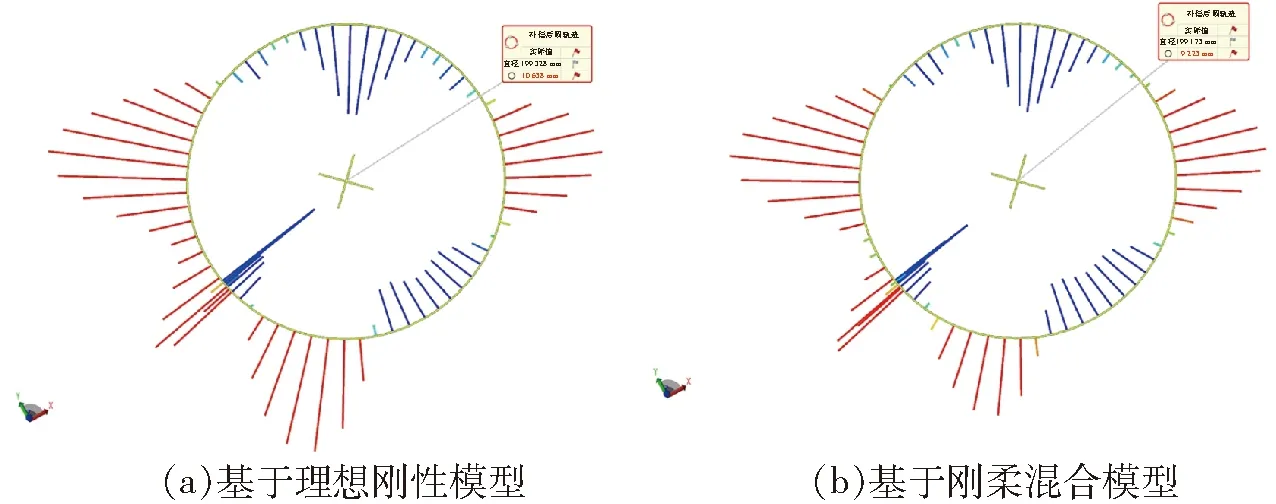
图14 带载情况下的轨迹跟踪实验Fig.14 Trajectory tracking experiments with payload

表2 圆周轨迹跟踪测量结果Tab.2 Circular trajectory tracking results mm

由表2可知，基于刚柔耦合模型的控制方法在轨迹跟踪精度上优于基于刚性模型时的精度。这说明利用稳定因果解实施控制能提高刚柔耦合并联机器人的空间轨迹精度，从而验证了该方法的有效性。必须指出，实验过程中定位靶标的实际测量轨迹与末端执行器的真实运动轨迹存在偏差。由于单台激光跟踪仪无法测量动平台的旋转运动，所以该偏差很难通过定量计算加以分析和补偿。为解决该问题，未来可通过修改动平台的结构来提高系统的轨迹测量精度。

为进一步验证动力学模型及求解方法的有效性，在第1支链柔性杆外壁上选择3个特征点，它们与上关节的距离依次为200、407.5、600 mm，在各个点处粘贴应变片并利用DH5927N型动态应变仪对其轴向的主应变进行测量，如图15所示。通过计算与测量发现，各特征点的主应变理论值以及实际测量值的变化趋势基本相同，因此以特征点1为例，对其主应变的理论计算值和测量结果进行分析和说明，如图16所示。

图15 柔性杆上的特征点Fig.15 Typical points on flexible link1.特征点1 2.特征点2 3.特征点3

通过对比图16a和16b中特征点1的主应变理论计算值与测量值可知，二者的变化趋势基本相同，而且都是在同一个数量级上发生变化，这进一步验证了理论模型与求解方法的有效性。但二者的变化范围具有一定的差距，其原因之一是测量应变前会进行调零平衡操作，它会消除测点的初始应变；另一个原因是建模过程中没有考虑各运动关节的装配间隙，运动过程中该间隙的变化会影响特征点的轴向主应变，使其在幅值和方向上产生偏差。因此，可对该间隙进行建模和补偿来进一步提高系统理论模型与轨迹跟踪的精度。表3是各个特征点处测量的正向主应变峰值和负向主应变峰值，通过变化幅度的对比可知，柔性杆中点处特征点的主应变变化幅度更小。

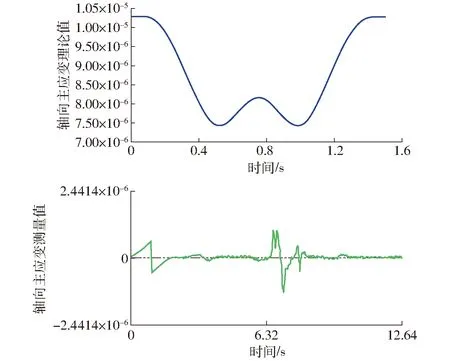
图16 特征点1处的主应变Fig.16 Axial principal stresses of typical point 1

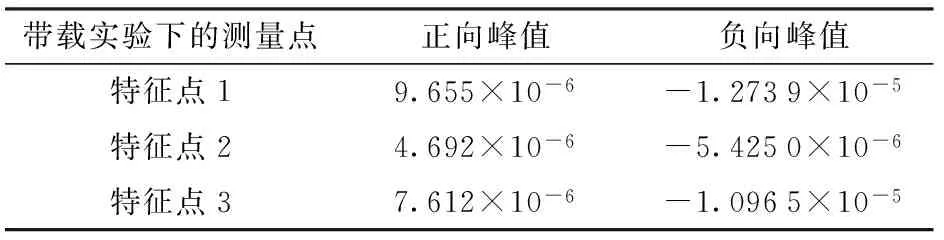
带载实验下的测量点正向峰值负向峰值特征点19.655×10-6-1.2739×10-5特征点24.692×10-6-5.4250×10-6特征点37.612×10-6-1.0965×10-5

5 结论

(1)针对空间刚柔耦合并联机构，提出了基于瞬态刚体校正法的动力学模型求解方法，该方法有效地解决空间闭链机构多体动力学模型在求解过程中出现的相容性问题，改善了系统综合收敛性能。

(2)从系统能量、初值点的选取、求解的稳定性与相容性等角度总结出刚柔耦合动力系统的求解策略，适用于求解具有闭链结构的空间多体系统的稳定因果解，由此构建的控制策略可提高并联机器人的轨迹跟踪精度。

(3)针对3-RRRU刚柔耦合并联机器人进行了仿真分析与实验对比验证，与基于刚性模型的控制方法相比，该方法将空间轨迹最大误差降低了0.372 mm，圆度误差降低了1.46 mm。通过对比柔性杆上特征点的主应变理论值与测量值，进一步验证了该理论模型与求解策略的有效性。

1 LONG P, KHALIL W, MARTINET P. Dynamic modeling of parallel robots with flexible platforms[J]. Mechanism and Machine Theory, 2014, 81：21-35.

2 郑恩来, 张航, 朱跃, 等. 含间隙超精密压力机柔性多连杆机构动力学建模与仿真[J/OL]. 农业机械学报, 2017, 48(1)：375-385. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170150 & journal_id= jcsam. DOI：10.6041/j.issn.1000-1298.2017.01.050.

ZHENG Enlai, ZHANG Hang, ZHU Yue, et al. Dynamic modeling and simulation of flexible multi-link mechanism including joints with clearance for ultra-precision press[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(1)：375-385. (in Chinese)

3 赵磊, 范梦然, 赵新华, 等. 柔性并联机器人非线性摩擦动力学建模与速度规划[J/OL]. 农业机械学报, 2017, 48(5)：390-396. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170550&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2017.05.050.

ZHAO Lei, FAN Mengran, ZHAO Xinhua, et al. Nonlinear friction dynamic modeling and velocity planning of flexible parallel robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(5)：390-396. (in Chinese)

4 邱丽芳, 王栋, 印思琪, 等. Deform-X柔性铰链设计与分析[J/OL]. 农业机械学报, 2017, 48(4)：370-376. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170449&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2017.04.049.

QIU Lifang, WANG Dong, YIN Siqi, et al. Design and analysis of Deform-X flexure hinge[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(4)：370-376. (in Chinese)

5 BAUCHAU O A, BETSCH P, CARDONA A, et al. Validation of flexible multibody dynamics beam formulations using benchmark problems[J]. Multibody System Dynamics, 2016, 37(1)：29-48.

6 MARTINI A, TRONCOSSI M, CARRICATO M, et al. Elastodynamic behavior of balanced closed-loop mechanisms: numerical analysis of a four-bar linkage[J]. Meccanica, 2014, 49(3)：601-614.

7 YU Y Q, DU Z C, YANG J X, et al. An experimental study on the dynamics of a 3-RRR flexible parallel robot[J]. IEEE Transactions on Robotics, 2011, 27(5)：992-997.

8 WU G L, BAI S P, HJØRNET P. Architecture optimization of a parallel Schönflies-motion robot for pick-and-place applications in a predefined workspace[J]. Mechanism and Machine Theory, 2016, 106：148-165.

9 LIANG D, SONG Y M, SUN T. Nonlinear dynamic modeling and performance analysis of a redundantly actuated parallel manipulator with multiple actuation modes based on FMD theory[J]. Nonlinear Dynamics, 2017, 89(1)：391-428.

10 ORZECHOWSKI G, MATIKAINEN M K, MIKKOLA A M. Inertia forces and shape integrals in the floating frame of reference formulation[J]. Nonlinear Dynamics, 2017, 88(3)：1953-1968.

11 IRSCHIK H, KROMMER M, NADER M, et al. The equations of Lagrange for a continuous deformable body with rigid body degrees of freedom, written in a momentum based formulation[J]. Journal of Sound and Vibration, 2015, 335：269-285.

12 SHABANA A A. Dynamics of multibody systems[M]. New York：Cambridge University Press, 2013.

13 WANG Z, TIAN Q, HU H Y. Dynamics of spatial rigid-flexible multibody systems with uncertain interval parameters[J]. Nonlinear Dynamics, 2016, 84(2)：527-548.

14 CHEN T, WEN H, HU H Y, et al. Quasi-time-optimal controller design for a rigid-flexible multibody system via absolute coordinate-based formulation[J]. Nonlinear Dynamics, 2017, 88(1)：623-633.

16 WANG J L. Application of Radau IIA algorithms to flexible multibody system with holonomic constraints[J]. Nonlinear Dynamics, 2017, 88(4)：2391-2401.

17 HUSSEIN B, NEGRUT D, SHABANA A A. Implicit and explicit integration in the solution of the absolute nodal coordinate differential/algebraic equations[J]. Nonlinear Dynamics, 2008, 54(4)：283-296.

18 ERLICHER S, BONAVENTURA L, BURSI O S. The analysis of the Generalized-α method for non-linear dynamic problems[J]. Computational Mechanics, 2002, 28(2)：83-104.

19 ARNOLD M, BRÜLS O. Convergence of the generalized-α scheme for constrained mechanical systems[J]. Multibody System Dynamics, 2007, 18(2)：185-202.

21 EBEL H, MATIKAINEN M K, HURSKAINEN V V, et al. Higher-order beam elements based on the absolute nodal coordinate formulation for three-dimensional elasticity[J]. Nonlinear Dynamics, 2017, 88(2)：1075-1091.

22 NACHBAGAUER K, GRUBER P, GERSTMAYR J. Structural and continuum mechanics approaches for a 3D shear deformable ANCF beam finite element：application to static and linearized dynamic examples[J]. Journal of Computational and Nonlinear Dynamics, 2012, 8(2)：021004-021004-7.