机械臂神经网络非奇异快速终端滑模控制

吴爱国 刘海亭 董 娜

(天津大学电气自动化与信息工程学院， 天津 300072)

0 引言

近些年来，机械臂在自动化领域发挥着重要的作用。随着现代工业的快速发展，它们已经被广泛应用于众多领域，其中许多任务需要高速度和高精度的轨迹跟踪控制。然而机械臂的动力学模型普遍存在许多不确定性和外部扰动，难以建立精确数学模型，给机械臂的精确控制带来一定的困难，所以研究机械臂高速度、高精度的轨迹跟踪控制具有重要意义。

针对机械臂轨迹跟踪控制问题已经提出了许多控制方法，比如PID控制[1]、迭代学习控制[2]、鲁棒控制[3]、自适应控制[4]、反馈线性化控制[5]以及模糊控制[6]等方法，其中终端滑模控制由于其有限时间收敛特性、对参数摄动和外部扰动的强鲁棒性，已被广泛应用于机械臂轨迹跟踪控制中。MAN等[7]首次提出终端滑模面的概念，相比线性滑模面，提高了系统在接近平衡点时的收敛速度，但该方法存在奇异性问题。为解决该问题，FENG等[8]提出非奇异终端滑模(NTSM)控制方法，并应用于机械臂轨迹跟踪控制，证明其有效性。李升波等[9]在此基础上提出了NFTSM控制方法，相比NTSM，提高了系统在远离平衡点时的收敛速度，实现全局有限时间快速收敛。最近，XIAO等[10]提出了一种基于观测器的串联机械臂轨迹跟踪控制方法，采用2个滑模观测器分别估计不确定运动学和未知动力学，但其动力学观测器是基于估计误差的，导致该方法在实际工程中难以实现。文献[11-12]采用RBFNN在线学习动力学建模误差，结合自适应边界技术估计学习误差和外部扰动的边界值，提高了控制精度。但以上这两种方法都需要依赖于机械臂的模型，限制了其实际应用价值。文献[13-14]研究了一种基于模型局部逼近的自适应终端滑模控制方法，采用RBFNN逼近被控对象模型矩阵的各个元素，实现无模型控制。但随着机械臂自由度的增加，控制器计算量将会急剧增加，不利于系统的实时控制，并且控制律存在不连续项，容易引起抖振。GUO等[15]提出自由漂浮空间机械臂约束自适应RBF-NTSM控制方法，考虑致动器的实际物理约束，采用RBFNN补偿有限的输入，实现空间机械臂在轨操作。WANG等[16]提出了基于时延估计的机械臂连续分数阶非奇异终端滑模控制方法，相比边界层技术获得更好的控制性能。但是该方法未考虑对估计误差的补偿，而是通过鲁棒项加以抑制，这就使得所设计的控制器具有一定的保守性，需要更大的切换

控制力矩，容易引起抖振。

针对上述问题，本文提出一种基于径向基神经网络RBFNN的非奇异快速终端滑模(NFTSM)自适应轨迹跟踪控制方法。

1 模型描述

基于拉格朗日方程的N关节机械臂的动力学模型表示为

(1)

M(q)——对称正定有界惯性矩阵，M(q)∈Rn×n

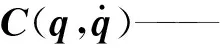
G(q)——重力项矢量，G(q)∈Rn

τd——外部扰动信号，τd∈Rn

τ——控制力矩矢量，τ∈Rn

假设1：假设期望轨迹qd∈Rn是一个二次连续可微的函数。

控制目标：设计合适的控制器，使关节输出q在有限的时间内跟踪期望轨迹qd。

定义系统跟踪误差及其导数为

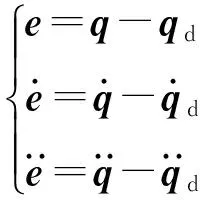
(2)

2 控制器设计

控制器的设计分为：①确定NFTSM滑模面，根据Lyapunov理论设计控制律。②设计合适的RBFNN逼近机械臂未知非线性动力学。控制系统的结构框图如图1所示。

图1 控制系统结构框图Fig.1 Block diagram of control system

2.1 控制律设计

为简化表达式，定义

(3)

设计滑模控制系统，首先需要建立合适的滑模面，以确保产生理想的滑动模态，然后设计滑模控制律驱动系统从任意初始状态到达滑模面。定义NFTSM滑模面为

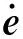
(4)

其中

α=diag(α1,α2,…,αn) (αi>0)

β=diag(β1,β2,…,βn) (βi>0)

式中r1、r2、r3、r4——正奇数，1r1/r2

李升波等[9]对式(4)进行了定量分析，从理论上证明其有限时间收敛性，本文在此只进行定性分析。当跟踪误差靠近平衡点时，即误差|ei|≤1时，忽略e的高次项，式(4)近似为

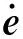
(5)

当系统处于滑模面，即s=0时，式(5)可表示为

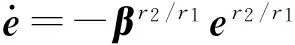
(6)

由于式(6)中e的指数小于1，则误差导数的绝对值大于相同参数的线性滑模面，克服后者收敛速度慢的问题。

同理当跟踪误差远离平衡点时，即误差|ei|>1时，e的高次项起主要作用，此时式(4)近似为

(7)

由于式(7)中e的指数大于1，故收敛速度高于线性滑模面。

建立了合适的滑模面，下一步是设计控制律驱动系统到达该滑模面。式(4)对时间求导可得

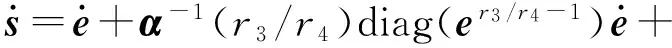
(8)

由式(1)和式(2)可知跟踪误差的二阶导数可被重新表示为

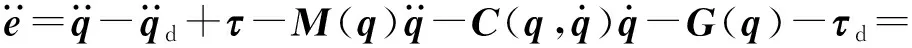
(9)

式中f——机械臂未知非线性函数

将式(9)代入式(8)，可得

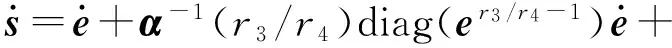
(10)

如果机械臂未知非线性函数f精确已知，可设计控制律为

τ=-f+τeq+τsmc

(11)

式中τeq——等效控制项τsmc——切换控制项

设计等效控制为

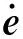
(12)

滑模控制系统利用切换控制律保证滑动模态的发生，传统切换控制采用不连续控制项ksmcsign(s)，但需要不确定性和外部扰动的上界先验知识。由于滑模系统只在滑动阶段才对模型不确定性和外部扰动具有不变性，为加快趋近阶段的速度，增强鲁棒性，本文提出快速连续终端切换控制律即

τsmc=-β(r2/r1)(λ1s+λ2sr5/r6+λ3sr7/r8)

(13)

其中

r5/r6>1 0λ1=diag(λ11,λ12,…,λ1n)
λ2=diag(λ21,λ22,…,λ2n)
λ3=diag(λ31,λ32,…,λ3n)

式中λ1i、λ2i、λ3i——正常数

2.2 RBFNN设计

神经网络具有学习和逼近任意非线性函数的能力，是控制许多复杂动力学系统的有力工具之一。相比多层感知器神经网络，RBFNN是一种特殊的网络结构，具有结构简单、快速学习和更好的逼近能力，不仅可以减少神经网络的参数调整的数目，还可以避免局部极小问题，满足实时控制的要求。因此，为解决控制器依赖机械臂模型的问题，利用RBFNN逼近未知非线性函数。

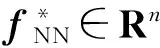
(14)

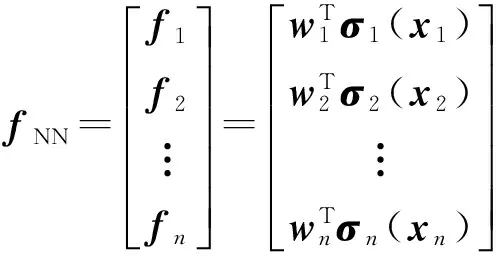
(15)

其中

wi=[wi1wi2…wiL]T

σi=[σi1σi2…σiL]T

式中fi——机械臂第i个神经网络的实际输出

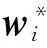
σi——第i个神经网络的高斯基函数

L——神经网络隐含层的节点数

高斯基函数表达式为

(16)

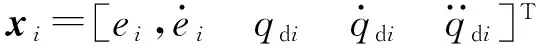
ci=[ci1ci2…ciL]
bi=[bi1bi2…biL]T

式中xi——第i个神经网络的输入向量

ci——第i个神经网络的中心矩阵

bi——第i个神经网络的基宽向量

由于神经网络存在逼近误差，传统方法是增大切换增益加以抑制，但这种方法具有一定的保守性，容易引起抖振。本文设计一个神经网络逼近误差自适应补偿项，进一步减小逼近误差对系统的影响。

因此控制量的输入可以被重新表示为

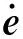
(17)

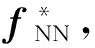
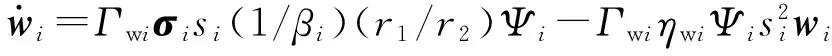
(18)

(19)

其中

式中Γwi、ηwi、Γεi、ηεi——正常数

3 稳定性分析

定理1：针对机械臂系统式(1)，当选用式(4)所示的NFTSM滑模面，式(17)的控制律和式(18)、式(19)的自适应更新律，则神经网络的权重和误差补偿有界，闭环系统全局渐进稳定。

证明：取Lyapunov函数为

(20)

V对时间t求微分可得

(21)

将式(10)和式(17)～(19)代入到式(21)可得

(22)

其中

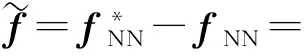
根据F-范数的性质可以得到

(23)

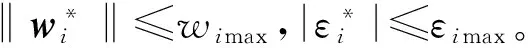
此时分以下3种情况考虑：

(24)

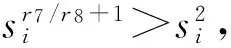
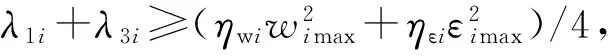
(25)

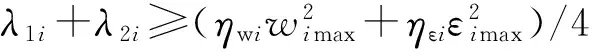
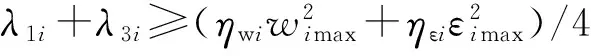
(26)

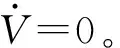
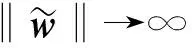
4 有限时间收敛性分析

证明：取Lyapunov函数为

(27)

Vs对时间t求微分可得

(28)

假设以下不等式成立

|ξi|≤βi(r2/r1)Kσi|si|

(29)

(30)

式中Kσi、Kεi——正常数

当满足以下不等式时，可保证式(29)、(30)成立

(31)

(32)

由式(31)、(32)可知，取滑模函数s满足

‖s‖≥max(Δ1,Δ2)=Δ3

(33)

将式(29)、(30)代入式(28)可得

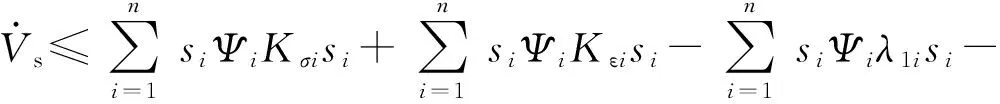
(34)

其中

λ1i>Kσi+Kεi

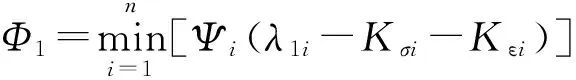
由文献[17]可得

(35)

将式(27)、(35)代入式(34)可得

(36)

其中

υ=(r7/r8+1)/2

由文献[17]可得有限收敛时间满足

(37)

由式(37)可知，滑模函数s将在有限的时间内收敛到邻域Δ3内。由式(31)、(32)可知，增大βi与r2的值或减小r1的值可使Δ3减小，Δ3越小跟踪效果越好。

5 仿真

为了验证本文所提的控制算法的有效性，选取6-DOF Denso 串联机械臂的前3个关节作为控制对象，其余3个关节锁死，并利用拉格朗日方程[18]建立该机械臂前3个关节的动力学模型，由于该模型方程比较复杂，在此没有具体列出。通过Matlab软件进行仿真研究，仿真采用式(17)控制律，记为NFT-T-RBF，采用式(18)、(19)自适应律，仿真参数如表1所示。

表1 NFT-T-RBF仿真参数Tab.1 Simulation parameters of NFT-T-RBF

为对比说明本文所提控制器的有效性，与以下3种控制方法的仿真结果进行对比。

控制器1：相比本文所提控制器，切换控制项采用不连续鲁棒项，记为NFT-S-RBF，控制律为

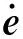
(38)

控制器1的仿真参数如表2所示。

表2 NFT-S-RBF仿真参数Tab.2 Simulation parameters of NFT-S-RBF

控制器2：相比控制器1，不再引入RBF神经网络估计系统未知非线性动力学，记为NFT-S，控制律为

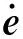
(39)

控制器2的仿真参数如表3所示。

表3 NFT-S仿真参数Tab.3 Simulation parameters of NFT-S

控制器3：相比控制器2，采用线性滑模面，记为SMC-S，该控制器的滑模面和控制律分别为

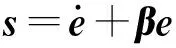
(40)

τ3=-k1s-k2sign(s)

(41)

控制器3的仿真参数如表4所示。

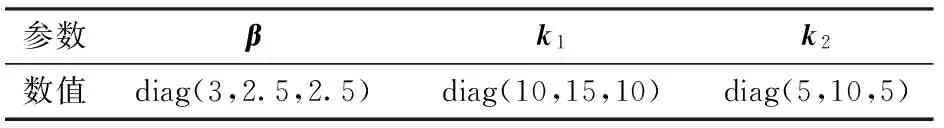
表4 SMC-S仿真参数Tab.4 Simulation parameters of SMC-S

机械臂3个关节的期望轨迹分别为

(42)

RBF神经网络隐含层的节点数L=7。

为验证所提控制算法的抗扰动性能，分别在3个关节通道的1、2、3 s时刻施加扰动，持续时间均为0.5 s，扰动值为对应关节控制量的限幅值的0.8倍，如图2所示。图3表示RBFNN对未知非线性函数的估计。图4为3个关节的轨迹跟踪曲线，期望轨迹均为正弦信号，其中前2个关节的期望轨迹的幅值为2π/3，第3个关节的幅值为5π/18。图5为3个关节的轨迹跟踪误差曲线。图6为各个关节的控制输出力矩。由图4和图5可以看出，4种控制器最终都能实现轨迹跟踪，但每个控制器的收敛速度、鲁棒性等又各有不同。

图2 外部扰动Fig.2 External disturbance

图3 不确定项估计Fig.3 Estimation of uncertainty

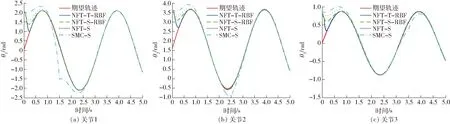
图4 关节轨迹跟踪曲线(仿真)Fig.4 Trajectory tracking curves of joints

图5 关节跟踪误差曲线(仿真)Fig.5 Tracking error curves of joints

图6 关节控制力矩(仿真)Fig.6 Control torques of joints

对比图4、5中的NFT-S与SMC-S，两者的主要区别是采用的滑模面不同，NFT-S控制器采用非奇异快速终端滑模面，SMC-S采用线性滑模面。由图4可以看出，对于在1、2、3 s时刻施加的外部扰动，SMC-S控制器对扰动更为敏感。由图5可看出，对于SMC-S控制器，外部扰动使3个关节产生的跟踪误差的峰值分别为1.8、0.4、0.2 rad，而对于NFT-S控制器，扰动产生的误差均在0.1 rad以内，误差峰值分别降低了94%、75%和50%。由图5可以看出，SMC-S控制器的调整时间约为2 s，而NFT-S控制器的调整时间为1 s，相比前者降低了50%。以上分析表明，非奇异快速终端滑模控制方法提高了滑模运动阶段的收敛速度，增强系统鲁棒性。

对比控制器1与控制器2，即图4～6中的NFT-S-RBF与NFT-S，NFT-S-RBF控制器利用RBF神经网络对系统未知非线性函数进行实时估计和补偿。由图4和图5可以看出，NFT-S-RBF控制器的抗扰动性能和系统收敛速度均略优于NFT-S控制器。由图6可以看出，NFT-S控制器的控制力矩输出产生了剧烈的抖振，这是由于切换控制项中的符号函数k2sign(s)造成的，而NFT-S-RBF控制器的输出力矩则更为平滑。以上分析表明，引入RBF神经网络估计系统不确定项能够有效地削弱系统抖振。

对比本文所提控制器与控制器1，即图4、5中的NFT-T-RBF与NFT-S-RBF，NFT-T-RBF控制器的切换控制项引入终端吸引子代替符号函数，使控制力矩输出连续。由图4和图5中可以看出，NFT-T-RBF控制器的调整时间均在0.3 s以内，降低了系统响应时间，并且进一步提高系统的抗扰动性能。因此切换控制项引入终端吸引子能够提高滑模趋近速度，增强鲁棒性。

仿真结果表明，本文所提出的基于径向基神经网络的非奇异快速终端滑模控制方法能够有效的提高系统控制性能，加快收敛速度，增强鲁棒性，抑制系统抖振。

6 实验

为了验证本文所提的控制算法在实际应用中的控制性能，在Denso 6-DOF机械臂的前3个关节上进行轨迹跟踪实验，其余关节锁死，该实验平台是Quanser公司开发的Denso 6-DOF机械臂控制系统，如图7所示。其硬件系统主要包括Denso VP-6242G机械臂，伺服控制器，控制计算机。软件系统为Quanser公司开发的能完全兼容Matlab的实时控制软件Quarc，用户可以在Simulink环境下调整内部控制器也可以独立设计控制器，通过该软件自动生成可执行文件。系统控制过程：编码器测量6个关节电动机的角度位置，通过专用电缆传送到伺服控制器的数据采集模块，再通过以太网传输到计算机，通过上位机控制器计算输出控制力矩，经数据采集模块送到伺服驱动器，驱动机械臂关节电动机运动，完成机械臂控制任务。

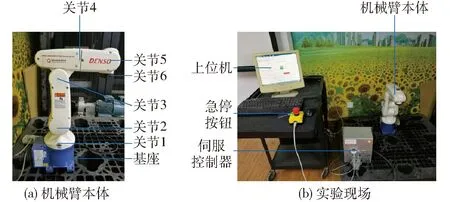
图7 实验平台Fig.7 Experiment platform

机械臂控制系统的关键运行参数如表5所示。

表5 关键运行参数Tab.5 Critical operating parameters

该实验是依据本文所提的控制算法以及仿真研究，独立设计控制器，实现机械臂轨迹跟踪控制。由于实际系统中存在信号传输延时问题，该系统延时为6个采样时刻，但在仿真中是不存在这种问题的，因此需要考虑系统延时对控制性能的影响，分析控制律式(17)可知，若滑模面的参数确定，其中等效控制τeq则为不可控的量。定义

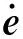
(43)

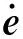
设某一次采样时刻为t0时刻，则该时刻所需要的等效控制量为

τeq(t0)=-βΘ(t0)

(44)

然而由于传输延时的影响，控制量τeq(t0)将在t1时刻作用于机械臂，但t1时刻机械臂真正需要的控制量为

τeq(t1)=-βΘ(t1)

(45)

如果机械臂控制系统是渐进稳定的，则满足

|τeq(t0)|>|τeq(t1)| (t1>t0)

(46)

这将会导致在t1时刻作用于机械臂的控制量的绝对值偏大，偏差量为

Δu=|τeq(t0)|-|τeq(t1)|=β[|Θ(t0)|-|Θ(t1)|]

(47)

偏差量Δu增大将会导致系统状态在滑模面附近抖振，由式(47)可知，β与Δu成正比，但β与提高系统收敛速度和稳态精度也成正比，使得减小偏差量与提高系统性能相悖，为了减小每个采样时刻的偏差量，削弱抖振，在实验中将式(12)修改为

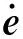
(48)

其中

φ=diag(φ1,φ2…,φn)(φi<βi)

实验采用式(17)控制律记为NFT-T-RBF，式(18)、(19)自适应律，实验参数如表6所示。

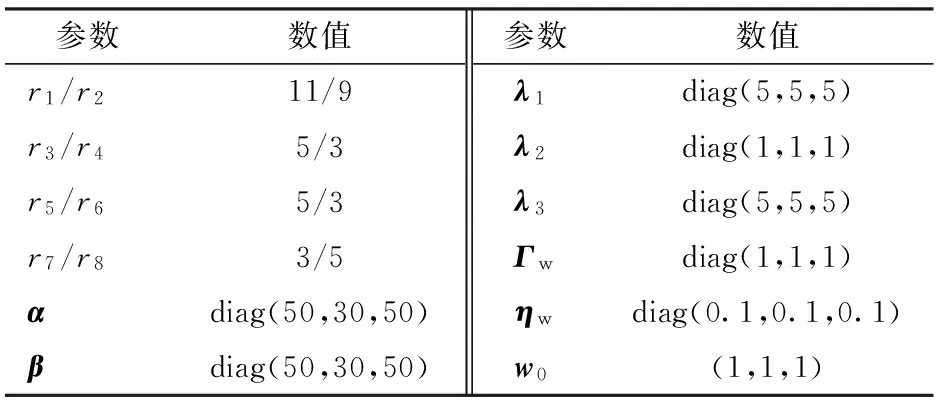
表6 NFT-T-RBF实验参数Tab.6 Experimental parameters of NFT-T-RBF

为对比验证本文所提控制方法的有效性，将实验结果与WAN等[19]所提出的基于扩张状态观测器的滑模控制方法(PD-ESO-SMC)进行对比。PD-ESO-SMC控制方法采用扩张状态观测器对系统不确定项进行实时的估计和补偿；滑模面采用线性滑模面，系统收敛速度慢，稳态精度低；切换控制引入sal函数，但该函数只能在滑模函数小于1时加快趋近速度，不能实现全局快速趋近。

PD-ESO-SMC方法所采用的滑模面和控制律分别为

(49)

τ=k2s+k3diag(|s|k4)sign(s)

(50)

PD-ESO-SMC方法的实验参数如表7所示。

3个关节的期望轨迹分别为

(51)

表7 PD-ESO-SMC实验参数Tab.7 Experimental parameters of PD-ESO-SMC

图8为关节轨迹跟踪曲线。图9为关节轨迹跟踪误差曲线。图10为各个关节的控制输出力矩。图11表示机械臂启动的初始化时间为2.85 s，在初始化完成以后采用用户独立设计的控制器完成各个关节的轨迹跟踪任务。由图8可以看出，本文所提的控制方法比PD-ESO-SMC方法具有更快的收敛速度。由图9可以看出，PD-ESO-SMC控制方法的误差稳态精度在0.02 rad左右，而NFT-T-RBF控制方法的稳态精度在0.005 rad左右，显著地提高了系统跟踪精度。由图10可以看出，输出控制量有轻微的抖振，但是在允许的范围之内。实验结果表明，本文所提控制方法在实际应用中能够提高系统收敛速度和跟踪精度。

图8 关节轨迹跟踪曲线(实验)Fig.8 Trajectory tracking curves of joints

图9 关节跟踪误差曲线(实验)Fig.9 Tracking error curves of joints

图10 关节控制力矩(实验)Fig.10 Control torques of joints

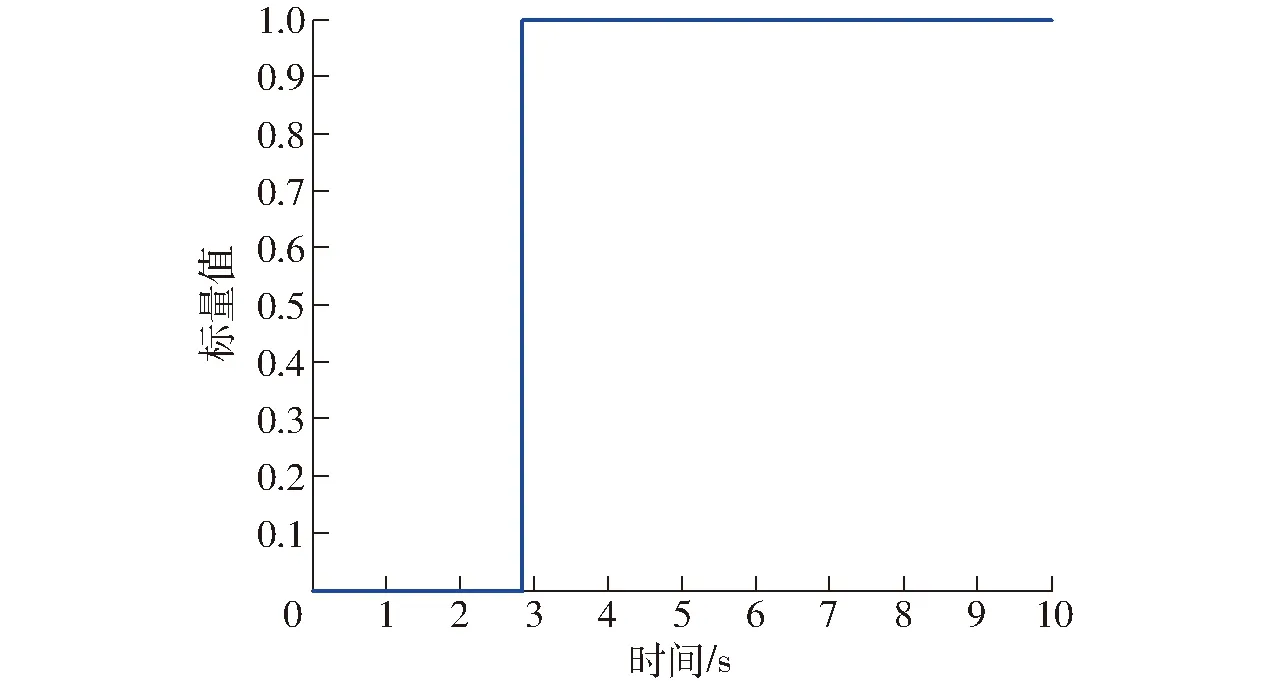
图11 系统初始化时间Fig.11 System initialization time

为衡量整个控制系统的平均跟踪精度，引入均方差的指标[20]比较两者的控制性能，即

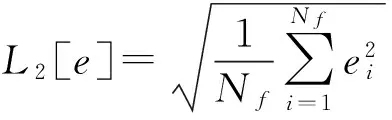
(52)

式中Nf——系统初始化完成以后的总采样数

则系统均方差指标如表8所示。

由表8可以看出，NFT-T-RBF控制方法在3个关节的均方差比PD-ESO-SMC的均方差分别降低了51.2%、41.0%和70.3%，表明本文所提的控制方法能够有效提高跟踪精度。

表8 均方差Tab.8 Mean square deviation rad

7 结论

(1)针对具有不确定性和外部扰动的机械臂系统存在收敛速度慢、跟踪精度低的问题，分析比较NFTSM和线性滑模的收敛性能，并结合RBFNN对系统未知非线性函数进行实时估计和补偿，实现无模型控制，以及切换控制项引入快速连续终端吸引子，提出了一种基于RBF神经网络的非奇异快速终端滑模控制方法，并证明了系统全局渐进稳定性和有限时间收敛特性。

(2)仿真结果表明，相比线性滑模，NFTSM使滑模运动阶段收敛速度提升约50%，3个关节的扰动误差峰值分别降低了94%、75%和50%，增强了系统鲁棒性。RBFNN补偿控制器在增强系统控制性能的同时有效地降低了系统抖振，使控制量输出更平滑。快速连续终端吸引子缩短了滑模趋近阶段的时间，进一步提高系统的抗扰动性能。

(3)实验结果表明，相比PD-ESO-SMC控制方法，本文控制方法的均方差分别降低了51.2%、41.0%和70.3%，有效地提高了系统跟踪精度。

1 ZHAO J B, WANG X Y, ZHANG G X, et al. Design and implementation of membrane controllers for trajectory tracking of nonholonomic wheeled mobile robots[J]. Integrated Computer Aided Engineering, 2015, 23(1): 15-30.

2 BOUAKRIF F, ZASADZINSKI M. Trajectory tracking control for perturbed robot manipulators using iterative learning method[J]. International Journal of Advanced Manufacturing Technology, 2016, 87:2013-2022.

3 HUANG D W, ZHAI J Y, AI W Q, et al. Disturbance observer-based robust control for trajectory tracking of wheeled mobile robots[J]. Neurocomputing, 2016, 198:74-79.

4 CUONG P V, WANG Y N. Adaptive trajectory tracking neural network control with robust compensator for robot manipulators[J]. Neural Computing and Applications, 2016, 27(2):525-536.

5 CAMBERA J C, FELIU-BATLLE V. Input-state feedback linearization control of a single-link flexible robot arm moving under gravity and joint friction[J]. Robotics & Autonomous Systems, 2017, 88:24-36.

6 FATEH M M, AZARGOSHASB S. Discrete adaptive fuzzy control for asymptotic tracking of robotic manipulators[J]. Nonlinear Dynamics, 2014, 78(3):2195-2204.

7 MAN Z H, PAPLINSKI A P, WU H R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators [J]. IEEE Transactions on Automatic Control, 1994, 39(12):2464-2469.

8 FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators [J]. Automatica, 2002, 38(12):2159-2167.

9 李升波, 李克强, 王建强, 等. 非奇异快速的终端滑模控制方法[J]. 信息与控制, 2009, 38(1):1-8.

LI S B, LI K Q, WANG J Q, et al. Nonsingular and fast terminal sliding mode control method[J]. Information and Control, 2009, 38(1):1-8. (in Chinese)

10 XIAO B, YIN S, KAYNAK O. Tracking control of robotic manipulators with uncertain kinematics and dynamics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10):6439-6449.

11 KUMAR N, PANWAR V, BORM J H, et al. Enhancing precision performance of trajectory tracking controller for robot manipulators using RBFNN and adaptive bound[J]. Applied Mathematics & Computation, 2014, 231:320-328.

12 YU L, FEI S, HUANG J, et al. Trajectory switching control of robotic manipulators based on RBF neural networks[J]. Circuits, Systems, and Signal Processing, 2014, 33(4):1119-1133.

13 TRAN M D, KANG H J. Adaptive terminal sliding mode control of uncertain robotic manipulators based on local approximation of a dynamic system[J]. Neurocomputing, 2017, 228:231-240.

14 PHAM C V, WANG Y N. Robust adaptive trajectory tracking sliding mode control based on neural networks for cleaning and detecting robot manipulators[J]. Journal of Intelligent & Robotic Systems, 2015, 79(1):101-114.

15 GUO S P, LI D X, MENG Y H, et al. Task space control of free-floating space robots using constrained adaptive RBF-NTSM[J]. Science China Technological Sciences, 2014, 57(4):828-837.

16 WANG Y Y, GU L Y, XU Y H, et al. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10):6194-6204.

17 YU S H, YU X H, SHIRINZADEH B, et al. Continuous infinite time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11):1957-1964.

18 霍伟. 机器人动力学与控制[M]. 北京: 高等教育出版社, 2005.

19 WAN K G, WU A G, LIU H T, et al. Trajectory tracking of 3-DOF spatial robot manipulator[C]∥2016 12th World Congress on Intelligent Control and Automation. IEEE, 2016:3259-3264.

20 丁力, 马瑞, 单文桃,等. 小型无人直升机航向线性自抗扰控制[J/OL]. 农业机械学报, 2017, 48(5):22-27.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170502&flag=1.DOI:10.6041/j.issn.1000-1298.2017.05.002.

DING L, MA R, SHAN W T, et al. Linear active disturbance rejection control for yaw channel of small-scale unmanned helicopter[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2017,48(5):22-27. (in Chinese)