具有时滞量及阻尼项的非线性双曲方程的振动性

，

(1.太原工业学院 理学系,山西 太原 030008；2.山西北方机械制造有限责任公司,山西 太原 030009)

近年来,具有时滞量与阻尼项的微分方程振动理论在生物学、医学、工程学等领域有着广泛的应用背景,进而,该类方程的振动理论取得了长足的进展[1～4].对于此类问题,通常采用Philos方法或Riccati变换进行研究,这样判定条件中需引入满足条件的H函数或待定函数φ(x)∈C1([t0,+∞),R+)研究方程的振动性,从而对方程振动性的判定增加了一定难度.本文利用微分不等式方法及微积分技巧讨论一类具有连续时滞量及阻尼项的非线性双曲方程

(x,t)∈Ω×R+≡G,R+=[0,+∞)

(1)

(2)

1 预备知识

(A3)m(t)∈C(R+,R+);

(A8)σ(ξ)∈([a,c],R)是非减函数且(1)中的积分为Stieltjes积分;

2 主要结果及证明

定理1 设微分不等式

(3)

无最终正解,则边值问题(1) (2)的所有解在G内是振动的.

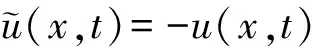
利用条件(A2)(A7)可知,总存在t≥t1>μ,使得w(t,ξ)≥μ,τi(t)≥μ,ρj(t)≥μ,则u(x,w(t,ξ))>0,(x,t,ξ)∈Ω×[t1,+∞)×[a,c];u(x,τi(t))>0,u(x,ρj(t))>0,(x,t)∈Ω×[t1,+∞)

在区域Ω上对方程(1)两边关于x积分得

(4)

由Green公式及边值条件(2)得

(5)

(6)

利用条件(A3)-(A6)及Jensen′s不等式可得

(7)

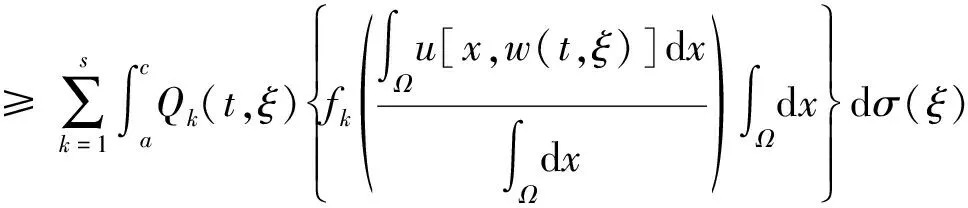
(8)

(9)

将(5)-(8)式代入(4)式中并结合(9)知,当t≥t1时有

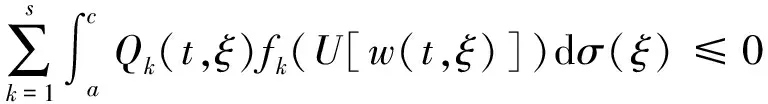
(10)

由(9)式易知U(t)是微分不等式(3)的一个正解,这恰与定理1矛盾,证毕.

定理2 对于方程(1)(2),假设条件(A1)-(A8)成立,若满足

(11)

(12)

则方程(1)(2)的每个解在G内是振动的,其中

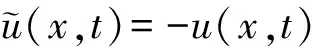
(13)

(14)

则(13)式可写为:

(15)

(16)

由(15)(16)式可得

(17)

因此易知V′(t)≤0.

下证,当t≥t1>0时,V(t)≥0,Y′(t)≥0.

假若V(t)<0,当T≥t1>0时,必有V(T)=a<0

(18)

对(18)式从T到t上关于t积分可得

(19)

对(19)式取极限并结合(11)式可知

这与Y(t)≥0矛盾,因此V(t)≥0,从而Y′(t)≥0.

由(14)式与条件(A2)及Y′(t)≥0可知

U(τi(w(t,ξ)))≤Y(τi(w(t,ξ)))≤Y(w(t,ξ))

(20)

(21)

将(21)式代入(17)式得

(22)

(23)

由条件(A7)及Y′(t)≥0易知Y(w(t,ξ))≥Y(w(t,a))

利用上式并结合(23)式可得

(24)

将(24)式代入(22)式可得

(25)

对(25)式在[T,t]上关于t积分,可得

(26)

对(26)式取极限并结合条件(12)有

这与V(t)≥0矛盾,定理2得证.

3 结束语

本文利用微分不等式方法及微积分技巧给出了一类含有连续时滞量及阻尼项的非线性双曲方程振动的两个充分性判定定理,定理2表明方程的振动性与时滞量τi(t),bi(t),w(t,a)及阻尼项系数m(t)有关,为某些工程领域的应用提供了一定的理论参考,同时,本文的判定定理中无需待定函数或满足条件的H函数,条件中出现的量均是方程中的已知参数或函数,方便非数学领域的专业人员使用.