基于真实教学的小学生发散思维的训练刍议

江苏连云港市海头中心小学 王二磊

《义务教育数学课程标准（2011年版）》特别强调：“为了适应时代发展对人才培养的需要，数学课程还要特别注重发展学生的应用意识和创新意识。”创新是生命力的体现，是追求突破的根本力量所在。因此，在小学数学教学中就得重视学生的数学思维训练，特别是发散思维的训练，通过发散思维的培养来实现发散思维流畅性、变通性和独创性等特性的递进，从而达成学习创新、思维创新的理想境界。诚如美国心理学家吉尔福特（Guiford）论述的那样：“正是在发散思维中，我们看到了创造思维最明显的标志。”

一、打牢厚实基础 引发思维发散

发散思维的培养不是空中楼阁，而是建立在真实的课堂教学、课堂训练之中的。因此，我们数学教学首先要盯牢“四基”训练，着力发展和提高学生的基础数学知识水平，夯实基本数学能力——算、看、思、联想等系列能力，努力发展学生的基本活动经验和基本数学思想方法等，进而在学习中产生积极的联想与发散，在知识的链接中寻得突破，获得创新的思路与解法。

【“圆柱和圆锥”的教学片段1】

师：今天我们主要学习圆柱、圆锥体积的相关知识，你有什么问题要咨询大家的呢？

生1：一个圆柱体底面直径4分米，高6分米，体积是多少立方分米？如果削成最大的圆锥，圆锥的体积是多少立方分米？

生2：这个不难，还可以设计成削去的体积是多大？

……

生3：把一个棱长为a厘米的正方体削成最大的圆锥，圆锥的体积是多少立方厘米？

生4：这个不是一样的啊！直接计算就行。

话音刚落，教室里一片哗然。“正方形的面积与圆的面积之间有这个关系吗？”“78.5%是怎么来的啊？”“真是会动脑子，把这么多的关系都用上了。”“我估计底面是正方形的长方体，也可以用这个方法，赶快举例来验证一下。”

……

课堂上的哗然，给予了我们更多的启示：教学的目的是什么？如何帮助学生建构有效的认知？怎样才能达成知识、技能、思维等训练同步跟进呢？案例中学生另辟蹊径，把诸多相关联的知识点串联在一起，巧妙地解决了正方体中削出最大圆锥体的问题。同时，教师的放手，也给学生留下争辩、求异的时空，让学习进入到一片神奇的天地之中。

从以上学生探究的过程可以看出：学生是可塑的，具有很强的模仿性，具有强劲的求异心理需求。因此，数学教学要立足最基本的认知、经验等积累，重视基本的思维训练，为学生对问题生成应急的灵敏感应、灵活运用知识、产生有效的联想、思路顺畅等提供保障，从而让数学学习变成探索之旅、创新之旅。

二、诱发积极联想 促发思维发散

思维的发散需要厚实的积累，也需要知识、经验、技能的支撑，特别是灵感的闪现，这样才能使学生思维活动不囿于某种暗示、某一框架，而具有举一反三、触类旁通的实效，能够巧妙地融合已知条件，产生积极的联想，沟通更多相关联的知识，使问题得以圆满解决。因此，在教学训练中要有意识地诱发学生的积极联想，促进学生变通，从而扩充发散思维的量，让数学学习闪烁着智慧的光芒。

【“圆柱和圆锥”的教学片段2】

师：请根据我们已经学习过的圆柱、圆锥体积以及它们之间的关系，设计一组有趣的练习，好吗？

（学生根据教师的提示，在小组中探讨、交流）

生1：一个圆柱的底面直径是6厘米，高10厘米。与它等底等高的圆锥体体积是多少立方厘米？

生2：太没水平了，这不是老师课上常讲的题目吗？我们的设计是：等底等高的圆柱和圆锥体积和是72立方分米，圆柱、圆锥的体积各是多少立方分米？

生3：还可以变成体积差。

生4：把一个半径为10厘米的圆锥形钢块，浸没在底面半径是30厘米的圆柱形水桶里。当钢材从水桶中拿出时，桶里的水面下降了1厘米。这个圆锥形钢材的高是多少？

生5：把一个底面直径6厘米，高10厘米的圆柱形木块削成最大的圆锥，削去的体积是多少立方厘米？

生6：把一个圆柱木块削成最大的圆锥，削去的体积是100立方厘米，你能算出圆柱和圆锥的体积各是多少吗？

生7：一段长方体木材，长、宽、高的比是4∶3∶2，木料的棱长总和为180厘米。如果把它加工成一个最大的圆锥，求这个圆锥的体积。

生8：不会吧！哪个面做底面啊？不是要考虑到三种情况吗？

……

在上述案例中，教师采取复习回顾、自主命题的策略来进行圆柱、圆锥体积的练习，这种设计不仅有利于学生深刻理解圆柱体积、圆锥体积的构成，掌握体积计算方法的推导过程，较为理性地把握准圆柱体积、圆锥体积之间的内在关系，更有利于学生掌握相关知识点的变形形式，明了知识点、知识线、知识面的相互联系。同时，还能诱发学生的发散思维，使其在出题能力、水平、新颖性等层面展开比拼，让数学学习变成命题游戏，变成竞赛活动。既规避了练习课单纯练的故旧范式，开创了一个崭新的窗口，又给我们的数学练习课带来了一股清新之风。

竞赛式的学生命题活动，第一，要求学生理清本单元中的知识要点，准确把握基本的知识架构；第二，还促使学生思考，因为你设计的问题，你得有相应的解题思路，否则就会被人“问倒”，所以促使学生试水，再下水；第三，比拼活动能够拓展学生的视野，丰富学习感知，更能使学生激发探究热情，提升思维的灵活性，促发思维的发散，让数学学习变得灵动且有趣。事实证明，一个人的兴趣愈浓厚、记忆系统中的知识越丰富，那么他数学思维的发散就越多，数学思维的发散性就越好，数学学习则更具活力，更具挑战性。

三、刺激求异心理 加速思维发散

善于选择具体题例，创设问题情境，精心诱导学生的求异意识，是我们培养发散思维的有效路径。因此，在实际教学中，我们就要激发学生乐于求异，并以此生发强劲的内驱动力，引导学生在求异中发展发散思维，提高发散思维能力。上述案例中的竞赛式命题活动就是一种刺激，一种动力催化剂。同样，我们在日常教学中要注重这方面的引入，用活动刺激学生的感官，激发学生的探究活力，让数学学习变成一种快乐的体验，成为一种追求更高境界的探索之旅。

【“圆柱和圆锥”的教学片段3】

师：经历了这么多的练习，大家的表现非常出色。不过老师还是想出一道题考考你们，有没有信心啊？

（学生都表现出一种期待）

课件呈现习题：

生：老师，不难啊！不就是先算出原来圆柱的体积，再除以2，就可以呀！

师：不错，有其他的思考吗？

（学生相互望着，有点茫然）

……

生：老师，我是这样想的，你们看行不行？把这半圆柱体的高再平均截成两段，然后拼起来，就成了底面半径是10厘米，高是10厘米的新圆柱体。然后求出新的圆柱体的体积就行了 （如箭头下方的图）。

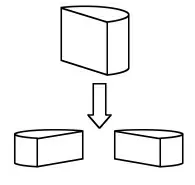
学生听后、看后，都露出惊讶的神色，纷纷拿笔计算起来。

生1：老师，我认为两种体积的计算方法都一样，都是：3.14×10×10×20÷2=3140（立方厘米）。

生2：是的，计算看起来一样，但是第二种应该是：3.14×10×10×（20÷2）=3140（立方厘米）。可以看出解答的思路是不同的。

……

不满足既有的答案，而是静等鲜花再度盛开，这是一种教学机智，更是一种艺术。在上述案例中，当学生说出常规思路时，教师的评价是中肯的，但也是否定的，这种截然不同的提示，给学生以打击，也诱使学生去思考，“还有什么新方法？”“应该从哪个方面去突破呢？”当这些问题萦绕在学生的脑海中，思维的活力就会迸发出来，创新、求异的灵智也会在深思中显现。

特别是当某个学生想出新的思路时，其他学生不自觉地参与其中，画出草图，动笔计算，使解题与思维训练获得同步发展。面对学生的质疑：“老师，我认为两种体积的计算方法都一样，都是：3.14×10×10×20÷2=3140（立方厘米）。”无疑又掀起新一轮的学习争议，当学生提出“是的，计算看起来一样，但是第二种应该是：3.14×10×10×（20÷2）=3140（立方厘米）。可以看出解答的思路是不同的”时，无疑进一步阐明了解题与思维同步的重要性，这就给学生一种难以磨灭的印象。笔者认为，这样的探究过程学生的参与度提高了，学生的思维活力增强了，留给学生的记忆也必定是永久而难以忘却的。

“最不完美的创新要比完美的守成伟大一百倍。”文兰森的论述也给我们数学教师带来了诸多启迪。数学教学不只是知识传输、技能训练，而是着力于思维的训练。创新意识、求异意识的培养，才能使学生的学习能力、思维水平获得长足的发展。立足日常教学，相机渗透发散思维等训练，一定能改善学生的思维质态，让他们的数学学习充满智慧，洋溢着创新的气息，让学生体味到数学学习的快乐与幸福。♪