面向服务推荐的QoS成列协同排序算法

曹婧华,孔繁森,冉彦中

(1.吉林大学 机械与工程学院，长春130022; 2.吉林大学 计算机公共教学与研究中心,长春130012)

0 引 言

随着面向服务的架构(SOA)、软件即服务(SaaS)、云计算等新的软件架构思想和理念的不断发展，服务作为一种新的软件资产正逐步兴起。网络上满足相同功能属性而非功能属性不同的候选服务日益增多，服务质量(Quality of service，QoS)逐渐成为服务消费者(用户)进行服务选择的重要依据。在实际应用中，由于Internet的不可预测性和用户环境的差异性，导致不同用户体验到的QoS值往往存在较大差异[1]。因此，研究如何根据用户偏好对服务进行个性化推荐成为亟需解决的关键问题。

协同过滤作为推荐系统中最成功也最有影响力的一种技术，近年来被广泛应用于服务推荐过程。基于协同过滤的服务推荐方法使用QoS值来代表用户对服务的偏好，将推荐任务转化为预测用户-服务QoS矩阵的缺失值，进而根据预测的QoS值对未知服务进行排序，最后按照排序结果产生推荐列表。基于QoS预测的服务推荐方法存在以下问题：由于将均方误差(MSE)作为评价指标，系统以高准确度的QoS预测值为目标，生成的推荐结果不能准确地体现用户偏好。如果QoS预测值仅仅被用来产生推荐列表，那么预测值的准确度就显得不那么重要了，而QoS的正确排序才是解决问题的关键所在。

目前，研究者们提出将排序学习技术融合进推荐算法中[2]，依据学习到的项目排序模型来生成推荐列表，这种方法也称为协同排序[3]。协同排序直接使用排序评价指标作为推荐系统的优化目标，能够更加贴近用户偏好，提高推荐的用户满意度。按照学习样例的不同，协同排序一般可分为3类：点级(pointwise)、对级(pairwise)、列表级(listwise)。点级方法为每个项目计算一个排序分数，类似于基于评分预测的方法；对级方法通过预测每对项目的相对顺序，得到最终排序，其计算复杂度相对较高；列表级方法以整个项目的排序为输入，全面考虑不同项目的序列关系，被认为是最有发展潜力的协同排序方法。

基于上述问题，本文提出了一种用于服务推荐的QoS成列协同排序算法。首先建立矩阵因式分解模型，用以描述用户和服务的隐含特征信息，并选用计算复杂度较低的列表级损失函数作为矩阵分解模型的优化目标。同时，通过序列相似度挖掘用户间的近邻信息来进一步提高QoS排序的准确性。由于算法综合利用了协同过滤和列表级排序的优势，可以更好地实现基于用户偏好的个性化服务推荐。

1 相关工作

根据所使用的方法或技术不同，协同过滤用于服务推荐的方法主要分为2类：基于内存的方法和基于模型的方法。

基于内存的方法根据相似用户或服务间的QoS历史记录进行预测。文献[4]提出了一种基于欧几里得距离的用户相似度计算方法，并依据相似用户之间的历史信息对目标用户进行个性化的QoS预测。Zheng等[5]提出了一种基于用户和基于服务的混合协同过滤QoS预测方法WSRec，使得QoS矩阵中的近邻信息得到更充分利用。文献[6]提出将用户和服务按自身特性和区域信息进行分类，然后对不同类别用户和服务进行更复杂的混合协同过滤QoS预测。文献[7]依据“预测得到的QoS值不会改变两个用户或服务的相似度”的假设，对传统协同过滤的预测方法进行了全新设计。文献[8]针对传统相似度计算方法(PCC或余弦相似度)的缺陷，通过对QoS矩阵行(列)向量进行正规化，然后再进行相似度计算，实现了一种基于正规化相似度的协同过滤方法NRCF。

基于模型的方法认为QoS值由用户和服务的隐含特征共同决定，通过建立合理的模型来进行QoS预测。Zheng等[9]利用矩阵因式分解模型建立起用户和服务的隐含特征矩阵，并通过挖掘用户的近邻信息来进一步优化预测模型，从而实现对未知QoS值的合理预测。文献[10]提出了一种结合近邻信息的非负矩阵分解算法，将QoS预测问题转化为稀疏QoS矩阵下的模型参数期望最大化估计问题。文献[11]考虑QoS信息在时间上的变化，将QoS信息扩充为用户-服务-时间三维张量，并提出利用非负张量分解模型对问题进行求解。

上述方法都以QoS值的准确预测为目标，与QoS正确排序的服务推荐目标存在偏差。例如，假设用户u1对服务s1、s2和s3的真实QoS值分别为(2，3，5)，使用两种不同的协同过滤算法进行预测得到两个结果：前者为(3，2，4)，后者为(1，2，3)。虽然前者的MSE小于后者的MSE，然而从排序的角度来说，后者预测得到了正确排序，因此要优于前者。

文献[12]意识到上述问题，提出了两种启发式的QoS排序预测算法CloudRank1和CloudRank2。利用相似用户的偏好信息计算每对服务的相对偏好度，然后对服务的偏好度进行累计，最后根据累计偏好度大小对所有服务进行排序，同时考虑已知QoS信息的服务在序列中的正确位置。该方法虽然在一定程度上解决了QoS排序预测问题，但是其需要计算每个用户的每对服务之间的相对偏好度，计算复杂度高，是典型的对级排序方法。

本文将利用列表级协同排序方法解决服务推荐问题，利用成列损失函数优化矩阵因式分解模型，并挖掘序列相似用户间的近邻信息，提高QoS排序的效率和准确性。

2 QoS成列协同排序算法

QoS为描述服务质量的一系列非功能属性集合，通常包括响应时间、吞吐量等，假设用户集合为U={u1,u2,…,un}，服务集合为S={s1,s2,…,sm}，QoS属性个数为q，则QoS信息可以用一个n×m的用户-服务QoS矩阵R表示，其中Rij={r1,r2,…,rq}，表示用户ui调用服务sj时的QoS信息。在实际应用中，QoS矩阵R中含有大量的缺失项，服务推荐的目标就是利用已有的QoS信息，对目标用户的未知QoS服务进行个性化推荐。与大多数研究工作一样，本文将只考虑单个QoS属性组成的QoS矩阵，对多个QoS属性进行联合服务推荐将作为下一步研究重点。

2.1 矩阵分解模型

矩阵分解模型认为QoS矩阵由少量的用户(服务)隐含特征决定，通过找到两个低维行满秩矩阵U和V(其中U为d×n矩阵，V为d×m矩阵，d为隐含特征因子的个数，且远小于n和m)，矩阵U的每一列相当于用户对于特征因子的特征向量，矩阵V的每一列相当于服务对于特征因子的权重。利用矩阵乘积X=UTV对QoS矩阵R进行拟合，则R中的缺失项就可以用X中对应位置的值进行预测，进而进行排序推荐。

上述问题中的矩阵U和V可以通过下式进行优化得到[13]：

(1)

式中：Iij为指示函数，当Rij不为空时，Iij=1；其他情况下为0;‖·‖F表示矩阵的F范数;λU和λV是为了防止过拟合而设置的正则化系数，为了简便起见，设置λU=λV=λ。

2.2 成列损失函数

可以看出，式(1)中的损失函数为使用矩阵分解模型得到的QoS预测值与真实QoS值之间的均方误差，是以预测值的准确度为目标的，与服务推荐的QoS正确排序不符。因此，本文选用文献[14]中的成列损失函数作为矩阵分解模型的优化目标。

文献[14]首先定义了一种称为TOP(Top one probability)的概率模型，表示一个服务在所有服务中QoS值排序第一的概率。具体而言，QoS值为Rij的服务sj在用户ui的服务排序中的TOP概率定义为：

(2)

式中：φ(x)为任意严格单调递增正函数，如文献[14]中选用的指数函数exp(x)。

假设存在两种服务的排序y和z，在得到所有服务对于目标用户ui的TOP概率之后，就可以利用两个概率分布之间的距离测度定义损失函数，如文献[14]中的互熵：

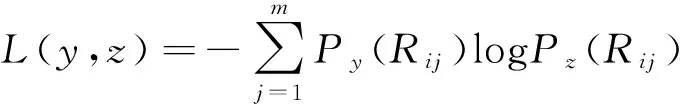
(3)

将式(3)引入到式(1)中，得到基于成列损失函数的矩阵分解模型：

(4)

从式(4)中可以看出，通过将成列损失函数引入到矩阵因式分解模型，不仅可以直接对QoS排序进行优化，而且相比点级和对级方法计算效率更高。

2.3 近邻信息的结合

矩阵因式分解模型难以利用相似用户(服务)间的有效排序信息，为了进一步提高QoS排序的准确性，本文提出将相似用户的排序偏好信息整合进协同排序过程中，详细步骤如下。

传统基于向量的相似度计算方法(PCC和余弦相似度)无法准确测度两个序列间的相似度，因此本文利用KRCC相关系数[12]计算两个用户u,v在QoS排序偏好上的相似度：

(5)

式中：N为用户u,v共同调用过的服务个数;C为其中排序一致的服务对个数;D为其中排序不一致的服务对个数。

可以看出，KRCC相关系数的取值为[-1,1]，当两个序列的顺序完全一致时，取值为1；当两个序列的顺序完全颠倒时，取值为-1。且N必须满足N≥2。

根据式(5)计算得到目标用户u与其他所有用户的相似度后，选择其中KRCC系数大于0且相似度最大的TOP-k个用户组成目标用户的相似用户集：

N(u)={v|v∈Tu,sim(u,v)>0,v≠u}

(6)

式中：Tu为与目标用户相似度u最大的TOP-k个用户。

目标用户u的QoS偏好应与相似用户集N(u)的QoS值相似，表现为在矩阵因式分解模型中，最终预测值为当前预测值与相似用户预测值的加权和：

(7)

式中：α(0<α<1)为平衡因子，wik为相似用户k在相似用户集N(i)中占的比重：

(8)

将式(7)整合进式(4)中，得到结合近邻信息的QoS成列协同排序模型(见式9)。目标函数(9)可以通过梯度下降算法来求得最优的用户和服务隐含特征矩阵U和V(见式(10)和式(11))：

(9)

(10)

(11)

式中：B(i)表示将用户i作为近邻用户的用户集。

2.4 算法及复杂度分析

将本文提出的结合近邻信息的QoS成列协同排序算法命名为NILMF(neighborhood integrated list matrix factorization)。NILMF算法的伪代码如算法1所示。

算法1(NILMF算法)

输出：完整QoS矩阵R

1 初始化U←Rand(d,n)，V←Rand(d,m)

2 For (i=1;i≤n;i++)

3 根据式(5)计算其他用户与用户i的相似度

4 根据式(6)得到用户i的近邻用户集N(i)

5endFor

6L0(U,V)=0

7For(t=1;t≤tmax;t++)

8If((Lt(U,V)-Lt-1(U,V))≤ε)then

9break

10else

11 根据式(10)和式(11)计算当前的梯度

12For(i=1;i≤n;i++)

14endFor

15 For (j=1;j≤m;j++)

17 end For

18 end f

19 根据式(9)计算当前Lt(U,V)

20 end For

21 X←UTV

22 用X中元素值取代R中对应的缺失项

23 output R

算法复杂度分析：损失函数的计算复杂度为O(Sd+SNd)，其中S为稀疏QoS矩阵R中的已观测项，d为隐含特征因子的个数，N为用户的平均近邻用户个数。梯度的计算复杂度分别为O(Sd+SNd+SMd+SNMd)和O(Sd+ShNd)，其中M为用户作为近邻用户的平均次数，h为用户的平均已观测项个数。因此，梯度下降一次迭代的计算复杂度为O(ShNd+SNMd)，由于h,N,M远小于S，所以复杂度与QoS矩阵R中的已观测项S成线性关系。

3 实验与分析

3.1 实验设计

为了验证NILMF算法的有效性，利用Matlab实现了该算法。实验数据集采用真实的QoS数据集WS-DREAM[1]，该数据集记录了位于30个国家的339个用户调用73个国家的5825个服务的QoS信息(包括响应时间QoS矩阵和吞吐量QoS矩阵)。为了便于分析，在实验中与文献[10]一样，从数据集中分别获取了300×3000的响应时间QoS矩阵和吞吐量QoS矩阵。

采用协同排序中最常用的评价标准NDCG[2]作为本文的评价标准。对于目标用户u，给定所有服务的QoS正确排序和预测排序，则前k个排序的NDCG@k值计算如下：

(12)

式中：DCGk和IDCGk分别为预测排序和正确排序的前k个服务的DCG值，其计算公式如下：

(13)

式中：reli为排序为i的服务的QoS值。可以看出，NDCGk取值范围为[0, 1]，值越大说明预测排序越接近正确排序。

为了验证NILMF算法的性能，与WSRec方法[5]、NIMF方法[9]、CloudRank1和CloudRank2方法[12]进行对比。其中，WSRec和NIMF方法为传统的基于QoS预测的推荐方法，CloudRank1和CloudRank2方法为启发式的基于对级排序的推荐方法。各算法的参数均取其默认值。

为了消除数据集的影响，将其分为5个不相关的300×600矩阵，每次实验分别对这5个QoS矩阵进行排序预测，最后取5次实验的NDCG@10均值作为实验结果。为了模拟现实情况，在每次实验中都随机移除矩阵中每行用户的若干项，即为每行用户留下given number数的已知QoS数据，得到不同given number下的QoS矩阵。在实验中，given number数以5为步长从5递增到50，研究算法在不同given number下的性能。算法的目标是根据这些已有的QoS信息对未知服务进行推荐，同时利用移除项的原值对算法进行评价。在没有特别说明的情况下，算法参数为：特征因子个数d为10，正则化参数λ为0.001，平衡因子α为0.3，近邻用户个数k为10，学习速率δ为0.001，迭代次数tmax为100。

3.2 实验结果与分析

图1和图2分别给出了在不同given number下，各算法在响应时间和吞吐量上进行排序预测的NDCG@10值的变化曲线。

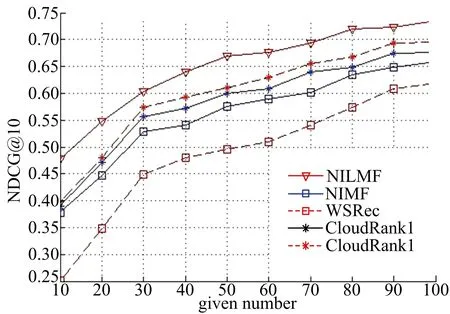
图1 响应时间数据集各算法实验结果Fig.1 The experiment results of each algorithm onresponse time dataset

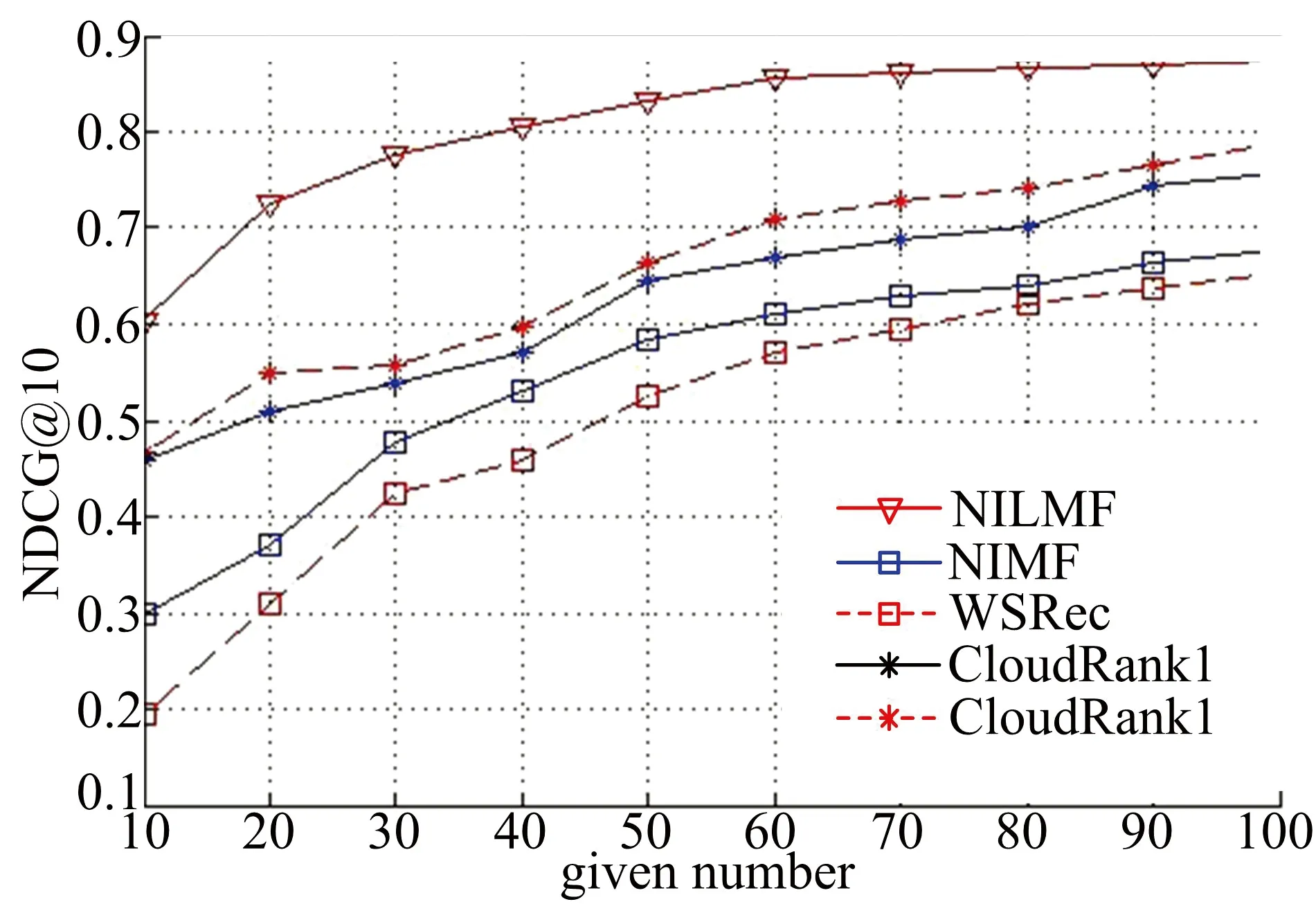
图2 吞吐量数据集各算法实验结果Fig.2 The experiment results of each algorithm onthroughput dataset

从图1和图2可以看出，随着given number的增大，各算法的NDCG值都呈上升趋势，即排序的准确性越来越好。这是由于随着given number的增多，可利用的QoS信息越来越丰富，越有利于各算法的近邻信息或(和)隐含特征的挖掘。从图1和图2中还可以看出，由于NILMF算法综合利用了矩阵分解和列表级排序及近邻信息的优势，在响应时间和吞吐量上的排序准确度上普遍优于其他方法；尤其当given number较少时，优势更加明显。WSRec方法在given number较少时，NDCG值呈现出较低值，这是由于WSRec方法根据用户和服务进行协同过滤，随着可利用QoS信息的减少，不可避免地影响其排序的准确度。

为了验证NILMF方法引进近邻信息以及利用KRCC系数计算用户间排序相似度的正确性，将NILMF方法与没有引进近邻信息的NILMF方法(记为LMF方法)、以及利用PCC系数计算用户间相似度的NILMF方法(记为NILMFPCC)进行对比。图3和图4分别给出了在不同given number下，三种算法在响应时间和吞吐量上进行排序预测的NDCG@10值的变化曲线。

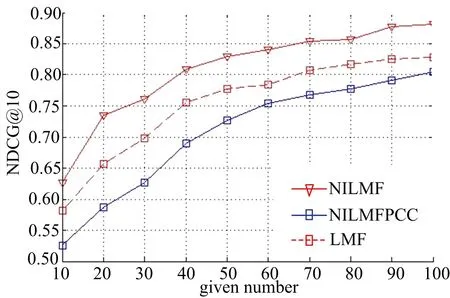
图4 吞吐量数据集近邻信息实验结果Fig.4 The neighbor information experiment resultson throughput dataset

从图3和图4可以看出，NILMF方法优于NILMFPCC方法，而NILMFPCC方法又优于LMF方法。这是由于LMF方法仅通过建立隐含特征矩阵对排序进行优化，难以利用相似用户(服务)间的有效排序信息；而NILMFPCC方法计算用户QoS向量之间的相关系数，当两个向量强相关时，只能说明两个向量越线性相关；而NILMF方法中的KRCC系数计算的是两个向量排序之间的相似度，更能准确挖掘相似用户间的排序信息，因此要优于其他算法。

为了研究参数α对算法性能的影响，图5和图6分别给出了平衡因子α在不同取值下的响应时间和吞吐量排序预测的NDCG@10曲线。其中，given number取值为100。

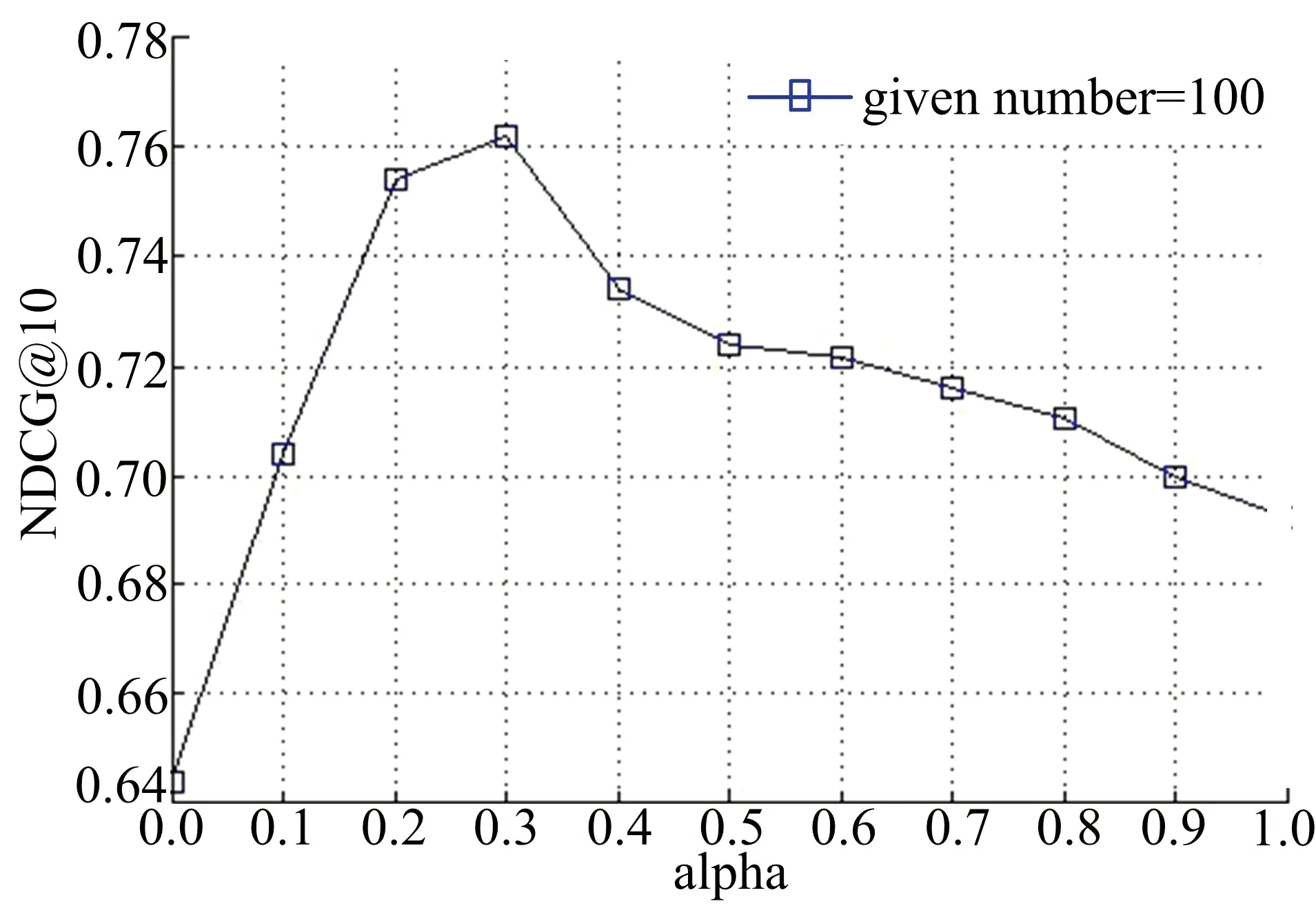
图5 响应时间数据集平衡因子实验结果Fig.5 The balance factor experiment results onresponse time dataset

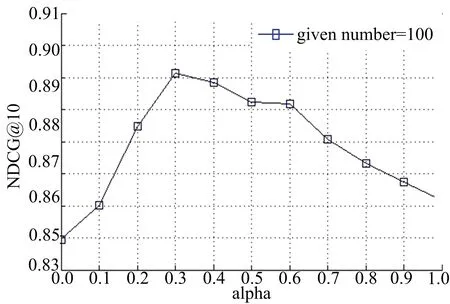
图6 吞吐量数据集平衡因子实验结果Fig.6 The balance factor experiment resultson throughput dataset

从图5和图6可以看出，当α取值为0～1时，NDCG值要大于α取值为0或1时的NDCG值，当α逐渐增大时，NDCG值首先呈上升趋势，当α超过某个特定阈值时，NDCG值又呈现出下降趋势，这从另一个方面又说明NILMF同时引入成列排序损失函数和近邻用户间有效排序信息的合理性。从图中还可以看出，当α取值为0.3时，NDCG取得最大值。这也是本文设置α默认为0.3的原因。

由于篇幅的原因，其他参数(如特征因子个数、最近邻用户个数)对算法性能的影响，在此不再赘述。

4 结 论

(1)针对传统基于QoS预测的服务推荐方法不能准确体现用户偏好的问题，提出了一种基于协同排序的服务推荐算法NILMF。将成列损失函数引入矩阵因式分解模型，综合利用矩阵分解模型和列表级排序的优势，实现了更贴近用户偏好的服务推荐。

(2)为了进一步挖掘相似用户间的QoS偏好，利用排序相似度KRCC计算得到用户的相似用户集，并将近邻用户的QoS偏好信息整合进列表级矩阵分解模型中，能够进一步提高QoS排序的准确性。

(3)在真实QoS数据集上的大量实验表明，相比于传统的基于QoS预测的方法和启发式的成对排序方法，NILMF算法的排序评价指标更好。实验同时还分析了不同参数对算法的影响。

[1] Zheng Z, Zhang Y,Lyu M R. Investigating QoS of real-world Web services[J]. 2014, 7(1):32-39.

[2] 黄震华, 张佳雯, 田春岐,等. 基于排序学习的推荐算法研究综述[J]. 软件学报, 2016, 27(3):691-713.

Huang Zhen-hua,Zhang Jia-wen,Tian Chun-qi.Survey on learning to rank based on recommendition alogorithms [J].Journal of software,2016,27(3):691-713.

[3] Balakrishnan S,Chopra S. Collaborative ranking[C]∥ ACM International Conference on Web Search and Data Mining，ACM, 2012:143-152.

[4] 邵凌霜, 周立, 赵俊峰,等. 一种Web Service的服务质量预测方法[J]. 软件学报, 2009, 20(8):2062-2073.

Shao Ling-shuang,Zhou Li,Zhao Jun-feng,el al.Web service QoS prediction.approach[J].Journal of Software,2009,20(8):2062-2073.

[5] Zheng Z, Ma H, Lyu M R, et al. QoS-aware web service recommendation by collaborative filtering[J]. IEEE Transactions on Services Computing, 2011, 4(2):140-152.

[6] 俞东进, 殷昱煜, 吴萌萌,等. 基于混合协同过滤的Web服务QoS预测方法[J]. 浙江大学学报：工学版, 2014, 48(11):2039-2045.

Yu Dong-jin,Yin Yu-yu,Wu Meng-meng,et al.QoS prediction for Web services based on hybrid collaborative filtering[J].Journal of Zhe jiang University(Engineering Science),2014,48(11):2039-2045.

[7] Ma Y, Wang S, Hung P C K, et al. A highly accurate prediction algorithm for unknown Web service QoS values[J]. IEEE Transactions on Services Computing, 2017, 9(4):511-523.

[8] Zheng Z, Chen J,Lyu M R. Personalized Web service recommendation via normal recovery collaborative filtering[J]. IEEE Transactions on Services Computing, 2013, 6(4):573-579.

[9] Zheng Z, Ma H,Lyu M R, et al. Collaborative Web service QoS prediction via neighborhood integrated matrix factorization[J]. IEEE Transactions on Services Computing, 2013, 6(3):289-299.

[10] 苏凯, 马良荔, 孙煜飞,等. 面向Web服务QoS预测的非负矩阵分解模型[J]. 浙江大学学报：工学版, 2015, 49(7):1358-1366.

Su Kai,Ma Liang-li,Sun Yu-fei,et al.Non-negative matrix factorization model for Web service QoS prediction[J],Journal of Zhejiang University (Engineering Science),2015,49(7):1358-1366.

[11] Zhang W, Sun H, Liu X, et al. Temporal QoS-aware Web service recommendation via non-negative tensor factorization[C]∥ International Conference on World Wide Web,2014:585-596.

[12] Zheng Z, Wu X, Zhang Y, et al.QoS ranking prediction for cloud services[J]. IEEE Transactions on Parallel & Distributed Systems, 2013, 24(6):1213-1222.

[13] Salakhutdinov R, Mnih A. Probabilistic matrix factorization[C]∥ International Conference on Neural Information Processing Systems, Curran Associates Inc,2007:1257-1264.

[14] Cao Z, Qin T, Liu T Y, et al. Learning to rank: from pairwise approach tolistwise approach[C]∥ International Conference on Machine Learning,ACM, 2007:129-136.