基于半陷门单向函数的公钥密码
赵 博, 秦贵和, 赵永哲, 杨文迪
(1.吉林大学 计算机科学与技术学院,长春 130012;2.华东师范大学 计算机科学与软件工程学院,上海 200062)
0 引 言
1976年,Diffie和Hellman[1]发表了著名文章《密码学的新方向”,文章引入了“公钥密码”的概念,并提出基于“陷门单向函数(Trapdoor one-way function)”来构造公钥密码的思想。不久,第一批公钥密码方案便被提了出来,它们分别是Merkle和Hellman基于背包问题的MH密码体制[2]以及Rivest、Shamir和Adelman基于整数分解问题的RSA密码体制[3]。随后Rabin、ElGamal、ECC等公钥密码体制也相继问世。
进入到21世纪,现有公钥密码(RSA、ElGamal、ECC等)日益受到量子计算的威胁[4,5],为了应对挑战,国际密码学界提出了“后量子密码学(Post-quantum cryptography,PQC)”的新学科方向。PQC的主要目标便是研究能抵抗量子计算的公钥密码(Quantum resistant public key cryptography),目前主要基于量子计算机不擅长计算的数学难题(比如NPC问题)来设计密码,该类密码主要有如下几个研究方向:基于格上困难问题的密码[6]、基于纠错码译码问题的密码[7]、基于多变量的密码[8]、基于辫子群(Braid Group)的密码[9]以及基于背包问题的密码[2,10]。
但目前所提出的抗量子计算公钥密码方案中的绝大多数都已被证明是不安全的。尽管不断有新方案被提出,但从构造方法来看,这些方案不外乎两大类:其一是基于“陷门单向函数”,这类公钥密码占绝大多数,其关键在于如何设计陷门。其二则是基于“非对称密钥交换”,其关键在于如何实现非对称的密钥交换,这往往要用到“单向函数”。一般说来,寻找单向函数要比寻找陷门单向函数容易得多,但单向函数不可逆,故不能直接用来实现公钥密码。而利用陷门单向函数虽可直接实现公钥密码,但由于“陷门性”和“单向性”的固有矛盾,使得二者很难兼顾。为了构造陷门,就必然要牺牲单向性;反之亦然。
本文重点研究了如何设计实现半陷门单向函数,以及如何基于半陷门单向函数来构造公钥密码。
1 半陷门单向函数的设计与实现
为了同时兼顾陷门性和单向性,本文引入了“半陷门单向函数(Semi-trapdoor one-way function,STOF)”的概念,其定义如下:
定义1 “半陷门单向函数”是一族“半可逆”的陷门函数:ft:X→Y,满足:
(1)已知ft和x∈X,计算y=ft(x)是容易的。

由于半陷门单向函数分别涉及单向性和陷门性,所以在设计时要同时对二者进行构思,这就需要选择合适的困难问题。为便于描述,文中常用的术语和基本符号如表1所示。

表1 基本符号
1.1 子集和问题与背包密码
“子集和问题(Subset sum problem,SSP,)”是“0-1背包问题”的一个特例。其定义如下:
SSP是著名的NPC问题。大多数背包密码都是基于SSP来构造的。为了保证解密的唯一性,公钥背包向量还必须满足USS(Unique Subset Sum),即唯一子集和条件。但已有的的背包密码通常无法抵御“低密度攻击”,背包向量的“密度”定义如下:

由文献[11-13],若DA>1,则A通常不满足USS条件。事实上,很多USS背包向量的密度都≪1。早期算法[14]可破解密度小于0.6463的背包密码,改进后算法[15]则可破解密度小于0.9408的背包密码。故为了抵御低密度攻击,公钥背包除应满足USS条件外,还应具有高密度(大于0.9408),但这二者往往很难兼顾,这也是设计背包密码的难点所在。
若DA<1∧DA≈1,则A中SSP通常有唯一解。而若DA>1∧DA≈1,则A中SSP通常有多解。这两种情形均易受到基于格的攻击[16,17]。只有当DA≈1时,对A中SSP无有效的解法。Impagliazzo和Naor亦证明,当DA=1时,求解A中SSP是最困难的[18]。多年来,对SSP最快的通用解法仍是Schroeppel和Shamir在1981年提出的[19],算法的时空复杂度分别为O(n·2n/2)和O(n·2n/4)。最近才有人对其进行了优化[20],但改进算法仍是指数级的,只是将时间复杂度降为O(n·2n/3)。
若在[1,2n]中均匀随机选择A=(a1,…,an),则A通常是难解的。实验发现,如此得到的A通常不满足USS条件。实际上,当DA≈1时,判定A是否满足USS条件亦是NPC问题[21]。
1.2 基于SSP的半陷门单向函数
可基于SSP的难解和易解性来设计半陷门单向函数。为此引入“半超递增背包向量”的定义如下:

显然,对于半超递增背包向量,可快速求出其SSP解的后半部,且易证如下定理:
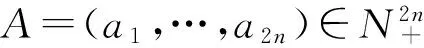
(1)A中SSP易解当且仅当A[1,n]中SSP易解。
(2)A为USS背包当且仅当A[1,n]为USS背包。
(3)若A[1,n]中SSP是难解的,则求解A中SSP的前半部亦是困难的。
基于半超递增背包向量,可得半陷门单向函数ft:{0,1}2n→N的设计方案如下:
(1)选择安全参数n;
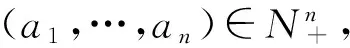
(4)随机选取M,W∈N+,其中:

(5)随机选取(1,2,…,2n)的置换π,并用(π,M,W)对A模乘变换得B=(b1,b2,…,b2n),其中bπ(i)=Wai(modM);
(6)以t=(A,π,M,W-1)为陷门(A不用全保存,仅保存A[n+1,2n]即可),并将B公开;
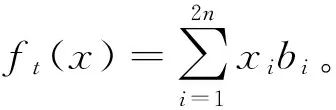
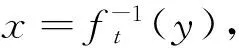
1.3 ft的安全性分析


(1)
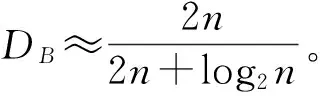
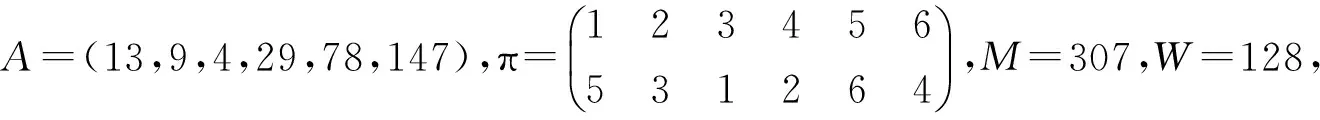
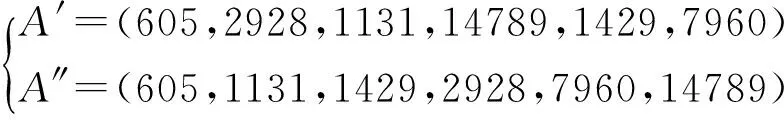
(2)


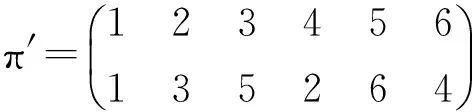
式中:m为满足1 (3) 由式(3)可得等价的陷门t′=(A″,π′,M′,U),从而完全破解ft,其中: 由于B是直接由A经模乘变换所得,故可基于Lenstra关于固定变元数量的整数规划问题可在多项式时间内求解,以及A的“半超递增”性来破解(M′,U)[14,22]。而ft在该攻击下是不安全的。 与MOOC融合的路径选择,是国内外图书馆界开展理论探讨与实践探索的重点内容。智力支持、技术支持、信息资源支持、实体空间支持,是图书馆与MOOC融合的4条主要路径。从已有研究内容看,国内图书馆界主要侧重论述通过开展版权服务、信息素养教育、嵌入课程辅导等提供智力支持,通过开展课程制作协助、学习者行为搜集分析与研判、MOOC平台技术优化等提供技术支持来与MOOC进行融合。然而,目前国内支持MOOC发展的相关政策及法律环境尚不完善,图书馆现有智力资源、技术力量与MOOC的发展需要尚不匹配,图书馆所能提供的智力支持和技术支持与国内现阶段MOOC发展的实际需求之间相差较远。 改进思路是使(xπ(n+1),…,xπ(2n))不是由(xπ(n+1),…,xπ(2n))∈{0,1}n直接经模乘变换得到,而是由无明显特征的背包向量经模乘变换得到,如此可使上述攻击无效,改进方案如下: (1)选择安全参数n。 (5)随机选取Δ=(δ1,δ2,…,δ2n)∈{-1,0,1}2n,ω∈ZM;并用(M,Δ,ω)对A进行变换得C=(c1,c2,…,c2n)=A+Δ·ω(modM),即: ci=(ai+δiω)(modM)(i=1,2,…,2n)。 (6)随机选取(1,2,…,2n)的置换π,并用(π,M,W)对C模乘变换得B=(b1,b2,…,b2n),即:bπ(i)=Wci(modM) (i=1,2,…,2n)。 (2)Fork=-n2Ton1Do S:=(SC-kω)(modM); Fori=2nDownto (n+1) Do If(S≥ai) Then xπ(i):=1; S:=S-ai; Else xπ(i):=0; EndIf EndFor Xk:=(xπ(n+1),…,xπ(2n)); 输出Xk; EndIf EndFor (4) 由于半陷门单向函数不能单独用来构造公钥密码。所以我们的方案构思是:以(ft,g)为公钥,t为私钥。这里ft:X→Y是半陷门单向函数,而函数g:X→Z则应满足: (1)由g和x∈X,计算z=g(x)是容易的。 问题的关键是:对于给定的半陷门单向函数ft,如何构造满足上述条件的函数g。 基于上述思路,本文给出了一种新的公钥密码方案,即STOF_PKC。STOF_PKC是基于第1节所构造的半陷门单向函数ft,以及F2上一个n×2n矩阵G来实现的,方案由密钥生成、加密、解密三个算法构成,具体如下: 2.2.1 密钥生成算法: (1)选择安全参数n; (2)构造半陷门单向函数ft,其陷门t=(A,Δ,ω,π,M,W),输出参数为B; (5)以t为私钥,(B,G)为公钥。 2.2.2 加密算法: 明文消息为x=(x1,x2,…,x2n)∈{0,1}2n{0},发送方对x加密过程如下: (1)获得接收方的公钥(B,G); (3)将密文(y,z)发送给接收方。 2.2.3 解密算法: (2)Fori:=1 TomDo EndFor (3)算法结束,所输出者即为候选明文(集)。 由STOF_PKC的解密算法,易知: (1)若明密文之间是一对一的,则密文经解密后可唯一确定明文。 (2)若明密文之间是多对一的,则密文经解密后能得到一个明文集合,且该集合恰好包含与给定密文对应的所有明文。 (3)若密文不对应任何明文,则密文解密后得空集。 理想情形是每一个密文都仅对应唯一的明文,此时不仅可提高解密效率,还可保证解密的唯一性。令明文空间P={0,1}2n{0},则STOF_PKC满足解密唯一性的充要条件是:不存在x,x′∈P(x≠x′)使ft(x)=ft(x′)∧G·x=G·x′。 设B的所有22n-1种非零子集和共有n_ss种取值,其中只与唯一子集和对应的取值共有n_uss种,则n_uss≤n_ss,且B满足USS条件当且仅当n_uss=n_ss。显然,若B满足USS条件,则STOF_PKC必满足解密唯一性。但这是NPC问题,无有效的判定算法。所以通过实验来对此进行分析,实验对不同的n,独立生成10 000个ft实例,然后对DB、n_ss、n_uss计算平均值,并统计B满足USS条件的出现数量,结果见表2。 表2 实验结果 由实验结果,可以看出: (5) 首先给出Semi-SSP(半子集和问题)的定义: (1)1≤i1 SSP和Semi-SSP的区别在于,前者对每个背包分量都要精确判定其是否属于给定的“子集和”,而后者只需对一半背包分量进行精确判定。若SSP可解,则Semi-SSP必可解,反之亦然。即Semi-SSP也是NPC问题。关于STOF_PKC的安全性,有: 定理2 破解STOF_PKC等价于求解B中的Semi-SSP。 (6) (7) (8) 对于n>16,由 (9) k=16,…,n-1 可得: (10) (11) 本文引入了“半陷门单向函数”的概念,并给出了基于半陷门单向函数来构造公钥密码的思路。在此基础上,给出了一种新的背包密码方案STOF_PKC,并证明了破解STOF_PKC等价于求解B中的Semi-SSP。因此,若B中的Semi-SSP是难解的,则STOF_PKC便是安全的。但尚有一些新问题有待解决,比如是否存在其他实现半陷门单向函数的方法、是否存在其他基于半陷门单向函数的公实现签名等,需要进行更深入的探索。 [1] Diffie W,Hellman M E. New directions in cryptography[J]. IEEE Transactions on Information Theory, 1976, 22:644-654. [2] Merkle R C,Hellman M E. Hiding information and signatures in trapdoor knapsacks[J]. IEEE Transactions on Information Theory, 1978, 24:525-530. [3] Rivest R L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the Acm, 1983, 26:96-99. [4] Shor P W. In algorithms for quantum computation: Discrete logarithms and factoring, foundations of computer Science[C]∥Proceedings on Symposium,Murray Hill,NJ,USA, 1994:124-134. [5] Grover L K. A fast quantum mechanical algorithm for database search[C]∥Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing,Philade lphia,PA,USA, 1996:212-219. [6] Poulakis D. On the cryptographic long term security[J]. Journal of Applied Mathematics & Bioinformatics, 2013,3(1):1-15. [7] Courtois N, Finiasz M, Sendrier N. In how to achieve a mceliece-based digital signature scheme[C]∥ International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 2001: 157-174. [8] Porras J, Baena J, Ding J Zhfe.A new multivariate public key encryption scheme[Z].Post-Quantum Cryptogaphy,2014:229-245. [9] Dehornoy P. Using shifted conjugacy in braid-based cryptography[J]. Computer Science,2006,418:65-73. [10] Okamoto T,Tanaka K,Uchiyama S. Quantum public-key cryptosystems[J]. International Journal of Theoretical Physics, 2011, 51:912-924. [11] Elkies N D. An improved lower bound on the greatest element of a sum-distinct set of fixed order[J]. Journal of Combinatorial Theory, 1986, 41:89-94. [12] Guy R K. Unsolved Problems in Number Theory[M].New York-Berlin:Springer-Verlag,2001:17-35. [13] Kate A, Goldberg I. Generalizing cryptosystems based on the subset sum problem[J]. International Journal of Information Security,2011, 10:189-199. [14] Brickell E F. Breaking iterated knapsacks[C]∥Advances in Cryptology, Proceedings of CRYPTO’84, Santa Barbara, California, USA, 1984:342-358. [15] Coster M J,Joux A, Lamacchia B A, et al.Improved low-density subset sum algorithms[J]. Computational Complexity 1999, 2:111-128. [16] Joux A. A practical Attack Against Knapsack based Hash Functions (Extended )[M].Berlin Heidelberg:Springer,1994:58-66. [18] Impagliazzo R, Naor M. Efficient cryptographic schemes provably as secure as subset sum[J]. Journal of Cryptology,1996,9:199-216. [19] Schroeppel R, Shamir A. AT=O(2n/2),S=O(2n/4) algorithm for certain NP-complete problems[J]. Siam Journal on Computing, 1981,10(3): 456-464. [20] Li Qing-hua, Li Ken-li, Jiang Sheng-yi, et al. An optimal parallel algorithm for the knapsack problem[J]. Journal of Software, 2003, 14(14):891-896. [21] Christos H Papadimitriou. On the complexity of unique solutions[J]. Journal of the ACM, 1984, 31(2):392-400. [22] Shamir A. A polynomial time algorithm for breaking the basic Merkle-Hellman cryptosystem[J].IEEE Transactions on Information Theory,1984,30(5):699-704.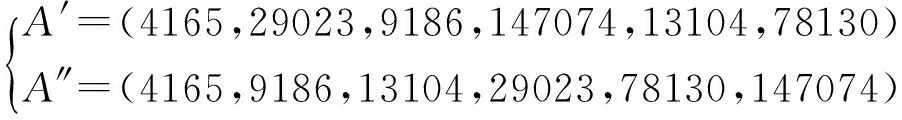
1.4 ft的改进方案

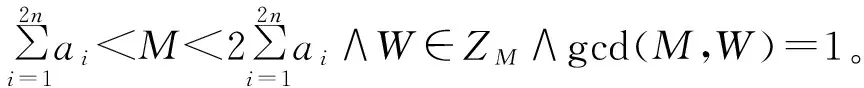
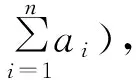

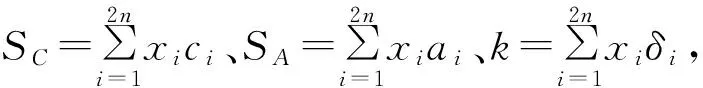


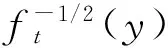
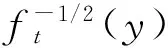
2 基于半陷门单向函数的公钥密码
2.1 方案构思
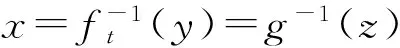

2.2 方案实现
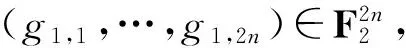

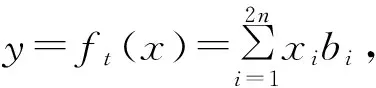
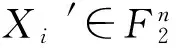
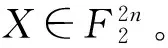
3 分析验证
3.1 STOF_PKC解密的正确性和唯一性分析
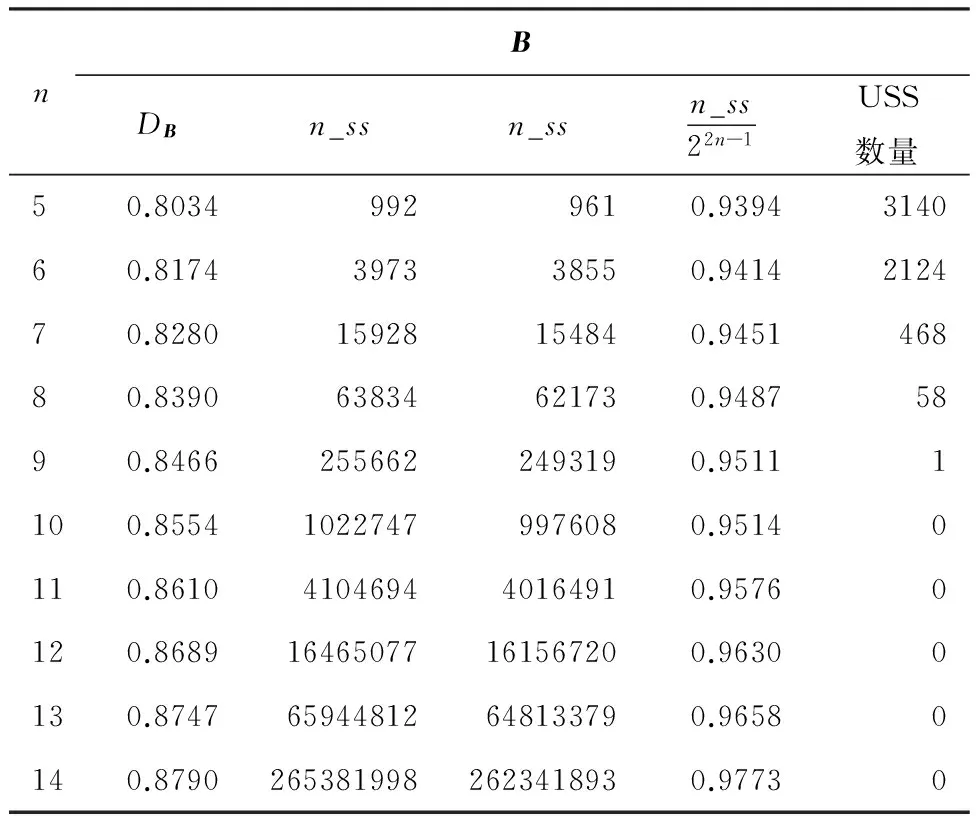

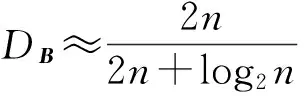
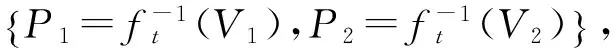
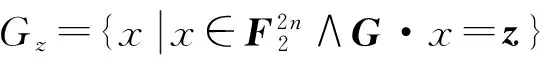

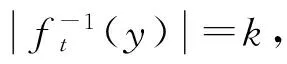


3.2 STOF_PKC的安全性分析


4 结束语

