基于倾角属性的三维地应力场分析方法*

熊晓军 崔泽飞 巫芙蓉 龚思宇 李 翔 刘 阳

(1.成都理工大学油气藏地质与开发工程国家重点实验室 四川成都 610059；2.中国石油川庆钻探工程公司地球物理勘探公司 四川成都 610213)

地层断裂带的发育与构造应力场关系密切，建立地层构造应力场可用于裂缝预测[1]。常规地应力场构建方法可以分为4类：第1类是基于经验关系式的方法，如贾立宏 等[2]提出的地应力场灰色模拟方法；第2类是进行应力场的数值模拟，如张帆 等[3]提出的构造应力场数值模拟方法；第3类是进行应力场的反演，如张国强 等[4]提出的基于神经网络结构分界的应力场反演方法；第4类是基于三维地震资料进行应力场的计算，如何英[5]提出的基于二维面曲率的应力场计算方法等。其中，第1类和第3类基于测井数据通过数学方法推算整个区域的地应力场，其结果缺乏准确性；第2类和第4类通过地质解释的构造信息计算地应力场，其结果分辨率较低。

为了克服上述4类方法的计算精度受目的层层位解释精度影响的缺陷，本文引入三维倾角属性对其进行改进。该方法首先采用基于离心窗扫描的倾角计算方法[6]，通过自动扫描地震数据获得地层倾角，进而计算地层曲率(相对于一般的中心窗和多窗扫描方法，离心窗扫描方法对地层细微构造的刻画更加精确[7])；然后再采用有限差分方法和Price(1990年)提出的“曲率-应变-应力”方程[8]计算地层构造应力场。渤海某工区花岗岩储层实际资料应用表明，本文方法的预测结果与测井解释的一致性较好，可以有效应用于研究区裂缝预测，并且具有一定的推广意义。

1 方法原理

1.1 基于地层倾角的地应力计算方法

地层曲率K是地层倾角Ψ关于弧长S的偏导数，即K=∂Ψ/∂s。当地层倾角Ψ较小时，Ψ≈tanΨ=∂z/∂x,z(x,y)表示地层曲面,弧长S≈x，则曲率可近似表达为K=∂2z/∂x2。为了方便后续的公式推导，在此定义变量Kxy，它的物理意义是地层的扭曲度。则地层在x方向(inline方向)和y方向(crossline方向)的曲率以及地层的扭曲度为

(1)

定义地层沿x和y轴方向的视倾角分别为p和q[9]。实际上p和q是地层在地震剖面上x和y方向的斜率[10],即曲面z(x,y)沿x和y方向的一阶偏导数

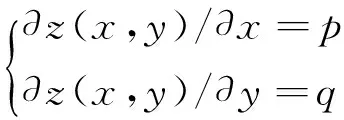
(2)

根据上述关系式可以推导出倾角表示的地层曲率方程为

(3)

因为p和q在剖面上是离散的，所以p和q对x和y的偏导数可以通过简单的显式有限差分方法[11]求出，即

(4)

(5)

其中，p1～p9在网格点[12]的位置如图1所示,q1～q9位置可参考图1。

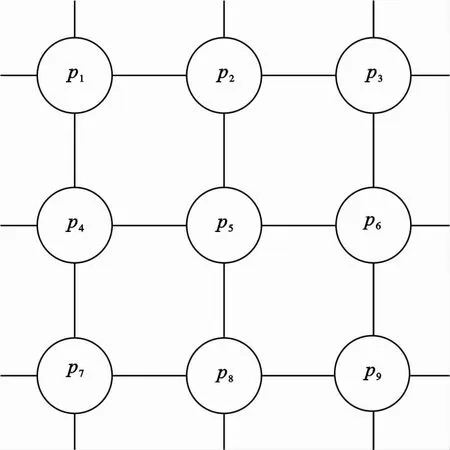
图1 离散数据点位置关系Fig .1 Location of discrete data points

在弹性力学中，根据变形几何方程和薄板假设理论，令曲面代表的地层时间厚度为0，则该地层在构造应力作用下的应变可以表示为

(6)

式(6)中：εx和εy分别表示x和y方向的应变;γxy表示剪应变;h表示地层厚度，在这里可以设为1。将式(3)代入式(6)中得应变与曲率的关系式为

(7)

由广义胡克定律，进一步得到应力与应变关系式

(8)

式(8)中:σx和σy分别表示x和y方向的应力;E代表杨氏模量;τxy表示剪应力；v代表泊松比。将式(7)代入式(8)可得曲率和应力的关系式为

(9)

至此在求得各方向的应力大小之后，可进一步求得目的层段的最大主应力大小及方向为

(10)

(11)

式(10)、(11)中：σmax为主应力;α为主应力与x轴的夹角。

因此，当我们计算得到目的层段的地层倾角p和q之后，可进一步基于曲率-应变-应力的关系得到地层倾角-应变-应力之间的关系，从而可以求得目的层段地层各个方向构造应力的大小，并进一步计算地层主应力的大小及方向。

1.2 基于离心窗倾角扫描的地层倾角计算方法

印兴耀 等[6]提出的离心窗扫描技术可以直接从地震资料中提取地层倾角，该方法将分析点周围的4个点依次作为中心点在x、y、t方向上开一个窗口扫描地震波形的相似性,扫描窗口在x、y、t方向上的延伸长度需要根据实际情况确定。离心窗扫描的计算方法如下：

Cij(t,p,q)=

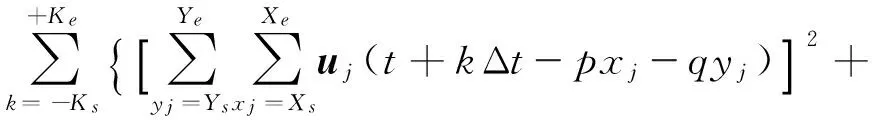
(12)

在确定了4个窗口在x、y、t方向上的延伸长度后，通过不断调整p和q的大小使相似性达到最大，这时的p和q即为该分析点的地层倾角。

1.3 基于倾角属性的地应力场计算流程

在通过弹性力学的变形几何方程和薄板假设理论推导出的地层地应力场方程即式(9)中，杨氏模量E和泊松比v可以利用地层的纵波速度(Vp)、横波速度(Vs)和密度(ρ)求解[13]，即

类似于叠后波阻抗反演中的速度建模方法[14]，选用多井层约束方法进行杨氏模量和泊松比的计算。

通过离心窗扫描获得地层倾角属性以及上述方法获得地层杨氏模量和泊松比，就可以计算地层的应力场，具体步骤如下：

1) 通过离心窗扫描目的层段的地震数据，计算地层倾角p和q;

2) 基于测井统计的纵、横波速度及密度参数，计算各井的杨氏模量和泊松比大小，并基于多井杨氏模量和泊松比参数进行目的层段的多井杨氏模量和泊松比建模;

3) 将研究区各点的倾角属性和杨氏模量代入倾角-应力方程即式(9)，计算目的层段各方向的构造应力大小，并进一步计算主应力的大小及方向；

4) 分析统计主应力大小及方向。

2 实例应用

将本文提出的基于倾角属性的三维地应力场分析方法应用于渤海某工区。该工区为大型花岗岩潜山油气藏区，风化壳储层在形成过程中受到区域构造应力的作用形成大量内幕小断层[15]，再由风化淋滤作用与风化剥蚀作用形成溶蚀缝和风化破碎带。裂缝系统是花岗岩潜山油气藏重要的油气运移通道[16]，所以研究地应力对该地区的油气开发具有重要意义。

图2为本文得到的研究区应力场方向示意图，每个小玫瑰图为剖分网格内的主应力发育方向，短线颜色代表方位角，蓝色代表低值，红色代表高值。图3为研究区测井方法得到的井点位置地应力玫瑰图。对比图2、3中井点位置处应力的大小与方向可以发现，除P2井外，2种方法结果一致。分析认为P2井位于工区边缘，可能受资料处理边缘效应的影响。 研究区裂缝发育与应力大小有密切关系，按照应力值的大小可以将工区分为3个区域：应力值在300～1 600 N/m2范围内为第1级强应力区，在0～300 N/m2范围内为第2级中应力区，在-300～0 N/m2范围内为第3级弱应力区。图4为本文方法得到的研究区应力场值分段统计分析结果，可以看出：强应力主要分布在工区西南部的2个条带状区域内；中应力为该研究区主要应力，呈条带状分布于整个区域；与强应力和中应力不同，弱应力连片分布于研究区若干个区域内，这也符合潜山沟谷的构造特征。研究区中有一些区域位于多方向应力交会的区域，这些地方应力场比较复杂，更容易发育裂缝。

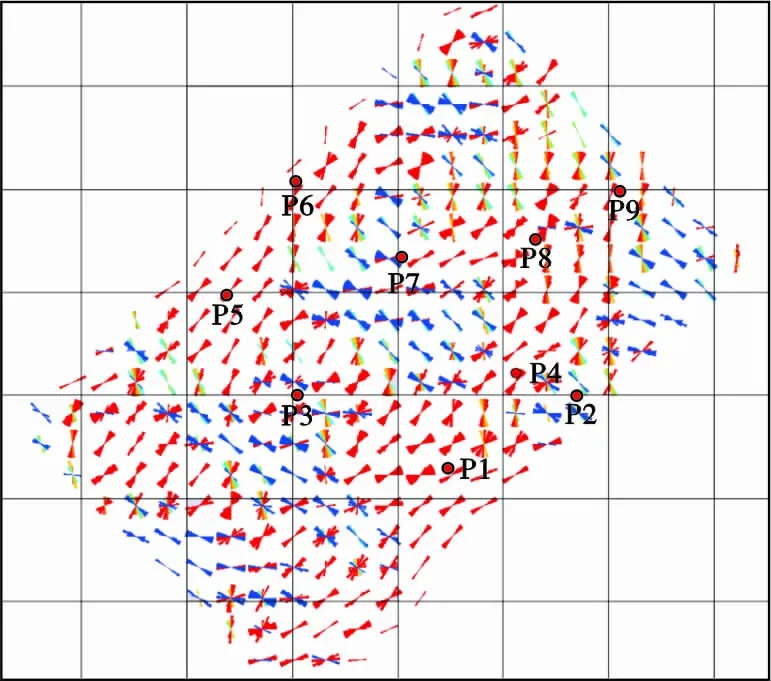
图2 本文方法得到的研究区应力场方向示意图Fig .2 Orientation diagram of stress field in the study area by the present approach

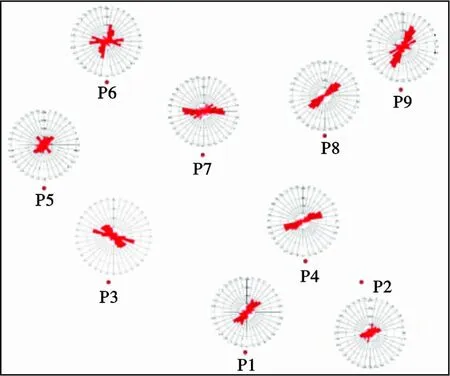
图3 研究区井点位置地应力玫瑰图Fig .3 Stress rose diagram of each well in the study area

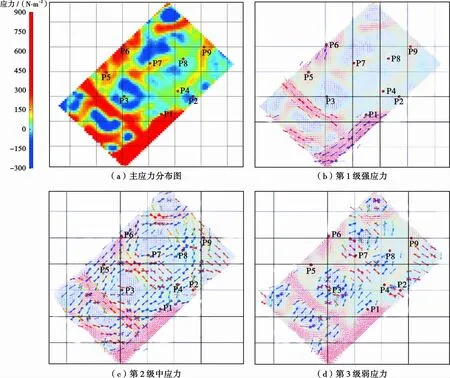
图4 本文方法得到的研究区应力场值分段统计分析结果Fig .4 Statistical analysis of different distribution of stress field in the study area by the present approach

3 结论

1) 本文方法根据地层倾角和曲率的关系，将曲率-应变-应力方程变形为倾角-应变-应力方程，实现了通过地层倾角计算地应力。

2) 本文方法借用了三维体曲率分析的思路，直接针对三维地震数据体进行计算，有效克服了常规方法受层位解释精度影响的缺陷，可以提高地应力场计算结果的准确性。

3) 渤海某工区花岗岩储层实际资料的计算结果表明，本文方法的预测结果与测井解释的一致性较好，能够较为准确地建立地层构造应力场，可以有效地应用于研究区的裂缝预测，并且具有一定的推广意义。

[1] 黄保纲,赵春明,杨庆红,等.等效应力场模拟与叠前弹性波阻抗反演综合预测锦州25-1南潜山裂缝储层[J].中国海上油气,2012,24(1):17-20.HUANG Baogang,ZHAO Chunming,YANG Qinghong,et al.Predicting fractured reservoirs in Jinzhou25-1S buried hill by comprehensively using equivalent stress-field simulation and pre-stack elastic impedance inversion [J].China Offshore Oil and Gas,2012,24(1):17-20.

[2] 贾立宏,李造鼎.地应力场灰色模拟方法研究[J].东北大学学报(自然科学版),1995,16(6):559-563.JIA Lihong,LI Zaoding.Methodical studies on grey simulation of In-Situ stress field [J].Journal of Northeastern University (Natural Science),1995,16(6):559-563.

[3] 张帆，贺振华，黄德济，等.预测裂隙发育带的构造应力场数值模拟技术[J].石油地球物理勘探,2000,35(2):154-163.ZHANG Fan,HE Zhenhua,HUANG Deji,et al.Structural stress field numerical simulation technique for fracture zone prediction [J].OGP,2000,35(2):154-163.

[4] 张国强，王桂萱.基于神经网络结构分界与FLAC的初始地应力场反演[J].大连大学学报，2007,28(6):43-47.ZHANG Guoqiang,WANG Guixuan.Back-analysis of initial ground stress field based on neural network ensemble and generation of the initial ground stress field by using FLAC [J].Journal of Dalian University,2007,28(6):43-47.

[5] 何英.高精度曲率分析及其在构造识别中的应用[D].成都：成都理工大学,2011.HE Ying.High precision curvature analysis and its application of structural identification [D].Chengdu:Chengdu University of Technology,2011.

[6] 印兴耀，高京华，宗兆云.基于离心窗倾角扫描的曲率属性提取[J].地球物理学报,2014,57(10)：3411-3421.YIN Xingyao,GAO Jinghua,ZONG Zhaoyun.Curvature attribute based on dip scan with eccentric window[J].Chinese Journal of Geophysics,2014,57(10):3411-3421.

[7] 杨威，贺振华，陈学华.三维体曲率属性在断层识别中的应用[J].地球物理学进展,2011,26(1):110-115.YANG Wei,HE Zhenhua,CHEN Xuehua.Application of three-dimensional volumetric curvature attributes to fault identification [J].Progress in Geophysics,2011,26(1):110-115.

[8] 黄炎.弹性薄板理论[M].北京:国防科技大学出版社,1992:10-50.

[9] MARFURT K J.Robust estimates of 3D reflector dip and azimuth[J].Geophysics,2006,71(4):29-40.

[10] Al-DOSSSARY S,MARFURT K J.3D volumetric multispectral estimates of reflector curvature and rotation [J].Geophysics,2006,71(5):41-51.

[11] ROBERT A.Curvature attributes and their application to 3D interpreted horizons [J].First Break,2001,19(2):85-100.

[12] COOKE D A,SCHNEIDER W A.Generalized linear inversion of reflection seismic data [J].Geophysics,1983,48(6):665-676.

[13] STEWART S A,WYNN T J.Mapping spatial variation in rock properties in relationship to scale-dependent structure using spectral curvature [J].Geology,2000,28(3):691-694.

[14] BERGBAUER S,MUKERJI T,HENNINGS P.Improving curvature analyses of deformed horizons using scale-dependent filtering techniques [J].AAPG Bulletin,2003,87(2):1255-1272.

[15] 谭成轩,王连捷,孙宝珊,等.含油气盆地三维构造应力场数值模拟方法[J].地质力学学报，1997，3(1)：71-79.TAN Chengxuan,WANG Lianjie,SUN Baoshan,et al.An approach to numerical simulation of 3-D tectonic stress field of the oil-gas-bearing basin [J].Journal of Geomechanics,1997,3(1):71-79.

[16] 王雷，陈海清，陈国文,等.应用曲率属性预测裂缝发育带及其产状[J].石油地球物理勘探，2010,45(6):885-889.WANG Lei,CHEN Haiqing,CHEN Guowen,et al.Application of curvature attributes in predicting fracture-developed zone and its orientation [J].OGP,2010,45(6):885-889.