液体晃动对TLP泥浆罐侧壁的影响分析

祖 巍 韩文秀 王晓梅 唐晓晴 杨肖龙 李彦丽

(1.中海油能源发展装备技术有限公司工程设计研发中心 天津 300452； 2.天津大学建筑工程学院 天津 300072)

泥浆罐是海洋平台液体循环系统的重要组成部分，用于承载井口至泥浆泵之间的液体循环，其内部液体的晃动不仅会对泥浆罐自身结构造成一定影响，还可能对整个平台结构的安全性能造成影响。屈博志 等[1]基于旅大PSP上部液体储罐，采用ANSYS软件模拟了储罐内液体晃动对储罐结构的影响；刘刚[2]针对胜利油田渤海海洋平台5 000 m3储油罐安全可靠性及优化问题，采用ANSYS软件建立了海洋平台储油罐桩土相互作用模型，对平台储罐进行了动力响应分析和地震时程分析，分析液体晃动对储油罐的影响；周国发 等[3]采用Fluent软件对罐式集装箱在运输过程中罐体内液体晃动问题进行研究，分析了在车辆加速过程中罐体围壁所受冲击力的变化及罐体静压强的变化。

目前，针对泥浆罐液体晃动的研究大多是基于固定式平台，而对于顺应式平台研究较少。张力腿平台(Tension Leg Platform,TLP)具有半刚性、半顺应性的特点，正是由于这一特点，平台在风、浪、流等环境载荷作用下产生的运动响应较固定式平台更为明显[4]，因此，有必要对其上部泥浆罐的液体晃动问题进行分析。本文针对某TLP的设计参数，采用SESAM软件建立湿表面模型和质量模型，计算TLP的加速度极值；采用ANSYS软件建立上部泥浆罐及其内部液体有限元模型，将平台加速度极值作为惯性载荷输入，分别从强度和刚度2个方面分析泥浆罐内液体晃动对泥浆罐各侧壁的影响，并与静水压下的结果进行对比，以期为TLP泥浆罐侧壁设计提供思路和设计依据。

1 TLP加速度极值计算

1.1 有限元模型

本文研究的平台为传统型TLP，主船体为正方形，在GeniE模块采用Panel单元建立TLP船体结构的湿表面模型，根据三维势流理论计算波浪力；采用张力腿单元模拟张力腿筋键；采用Morison单元模拟立管，根据Morison方程计算波浪力。TLP有限元模型如图1所示。

1.2 加速度极值的计算

将有限元计算模型导入Wadam模块进行水动力计算。由于该TLP结构对称，因此浪向区间取0～90°，步长45°。波浪谱采用P-M谱，其表达形式为[5]

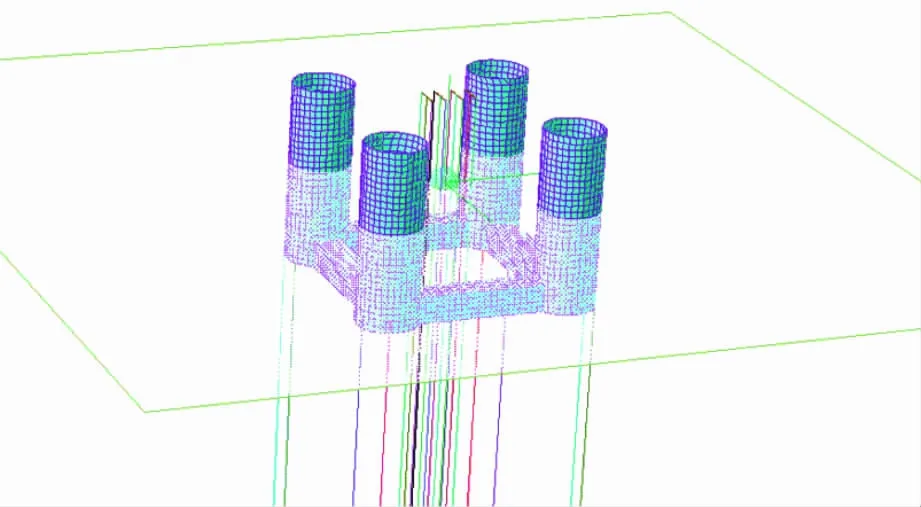
图1 TLP有限元模型Fig .1 Finite element model of TLP

(1)

式(1)中：HS为波浪有义波高， m；TZ为波浪平均跨零周期， s；ω为波浪频率， rad/s。

假设平台短期响应服从Rayleigh分布，则该分布的方差(σ2)可由平台响应谱得到[6]

(2)

式(2)中：Ha(ω|θ)为平台对应浪向下加速度RAO结果;Sa(ω|HS,TZ)为平台加速度响应谱；θ为波浪入射方向，(°)。

由此，可获得平台短期预报的各种统计值，包括均值、三一值、十一值等。本文采用SESAM软件，基于10年一遇正常作业工况(有义波高HS=6.5 m，谱峰周期TP=12.3 s)，取7%的升沉和横摇临界阻尼[7]，计算所得的TLP加速度极值如表1所示。

表1 TLP加速度响应极值Table 1 Extreme values of acceleration response of TLP

由表1可知：TLP的z方向加速度响应幅值远小于另外2个自由度的响应幅值，这是因为较大的预张力在极大程度上约束了平台的平面外运动，使平台的横摇、纵摇和垂荡3个自由度方向近似于刚性，而由于平台浮筒受到较大的水平方向波浪力，使得纵荡、横荡和首摇3个自由度方向近似于柔性。

2 泥浆罐有限元模型的建立

采用ANSYS建立泥浆罐有限元模型，其中泥浆罐各波纹板侧壁和底板采用shell63板单元模拟，底板支柱和梁结构采用beam188单元模拟，其内部泥浆液采用fluid80单元模拟。fluid80流体单元主要用来模拟无流速、盛装在容器中的流体，既适用于计算流体固体相互作用的静水压强问题，又可以考虑加速度效应来处理液体晃动问题，同时考虑了液体黏度和阻尼的影响。模拟中,液体密度取1.2 t/m3，黏度取1.2×10-6m2/s，杨氏模量取2.18×106kPa，泊松比取0.5。fluid80模拟泥浆罐液体晃动有限元模型如图2所示。

采用2种加载方式，其中模型1为静水压模型，即采用fluid80模拟液体静水压作用，共得到1种工况；模型2为液体晃动模型，即将TLP极值加速度作为惯性载荷，采用fluid80模拟泥浆罐内部80%液体，模型2计入8个波浪入射方向(0°、45°、90°、135°、180°、225°、270°和315°)的惯性载荷，共得到8种工况。模型的边界约束采用支柱最下端的固支约束，泥浆罐有限元模型如图3所示。

图2 fluid80单元模拟TLP泥浆罐液体晃动 有限元模型Fig .2 Fluid sloshing modeled by fluid80 of mud tank of TLP

图3 TLP泥浆罐有限元模型Fig .3 Finite element model of mud tank of TLP

3 液体晃动对泥浆罐侧壁的影响分析

将计算得到的平台各方向的加速度极值作为惯性载荷输入，对泥浆罐进行准静力分析计算，得到泥浆罐各侧壁的应力和变形。主要分析流程如图4所示。 取10年一遇正常作业环境条件作为计算工况，板材屈服极限为355 MPa[8]，提取2种模型各侧壁结构在不同工况下的最大应力和变形，对泥浆罐侧壁结构进行强度和刚度的校核。提取模型2在8个方向泥浆罐侧壁的最大应力、最大变形及最大值发生位置，提取模型1对应位置处的应力和变形值,如表2所示。由表2可知：

1) 波浪各入射角度下，泥浆罐侧壁强度和刚度均满足规范要求，最大应力为50.83 MPa，发生在模型2波浪90°入射方向，波纹板7中部位置;最大位移为8.60 mm，发生在模型2波浪180°入射方向，平板中部位置。

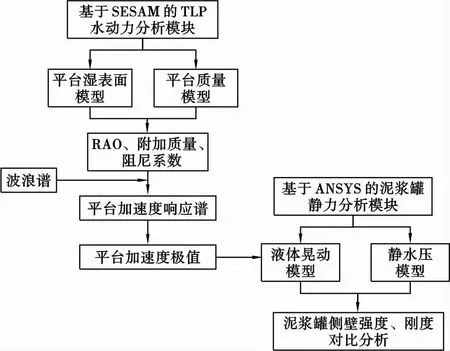
图4 TLP泥浆罐准静力分析流程Fig .4 Analysis process of mud tank of TLP表2 TLP泥浆罐侧壁校核结果Table 2 Checking results of mud tank wall of TLP

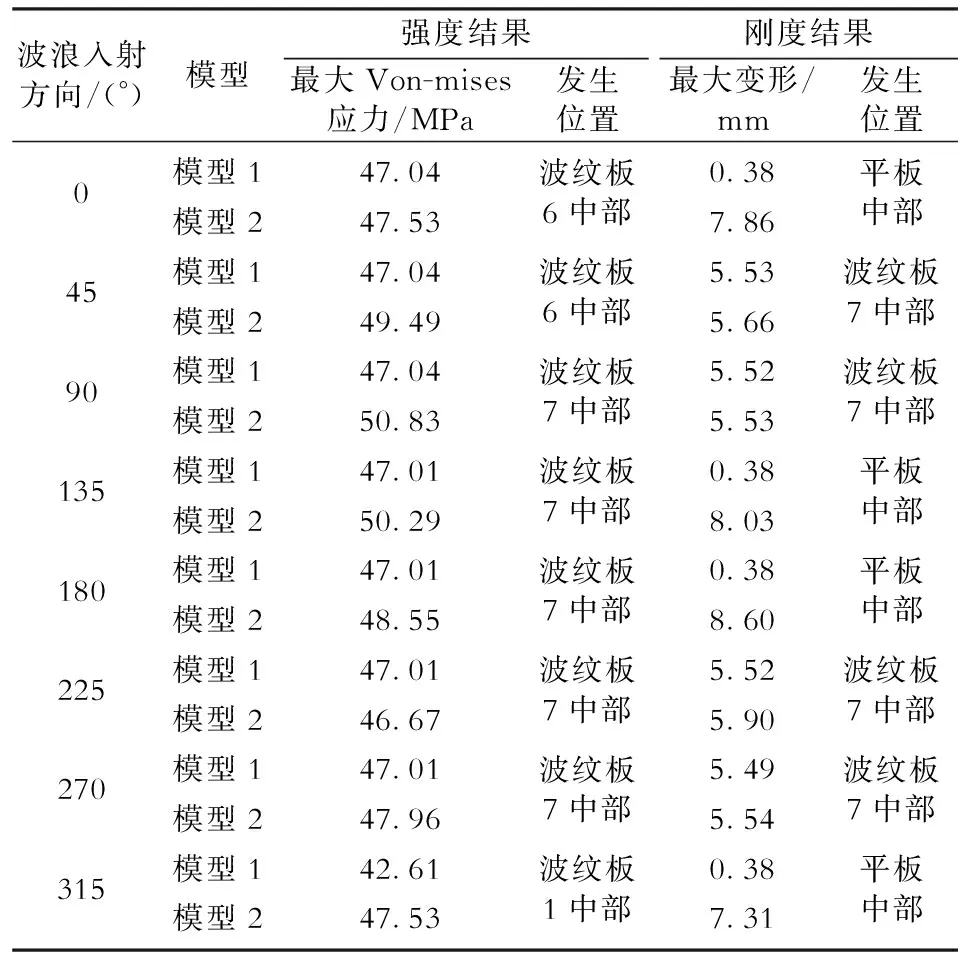
波浪入射方向/(°)模型强度结果刚度结果最大Von-mises应力/MPa发生位置最大变形/mm发生位置0模型147.04波纹板6中部0.38平板中部模型247.537.8645模型147.04波纹板6中部5.53波纹板7中部模型249.495.6690模型147.04波纹板7中部5.52波纹板7中部模型250.835.53135模型147.01波纹板7中部0.38平板中部模型250.298.03180模型147.01波纹板7中部0.38平板中部模型248.558.60225模型147.01波纹板7中部5.52波纹板7中部模型246.675.90270模型147.01波纹板7中部5.49波纹板7中部模型247.965.54315模型142.61波纹板1中部0.38平板中部模型247.537.31

2) 最大应力发生位置主要集中于波纹板1、6、7的中部位置，由于这3块波纹板较其他波纹板宽度较大，在液体静水压力和水平方向惯性载荷的联合作用下，波纹板中间位置承受较大弯矩，说明相同高度的波纹板随着跨距增加，垂直于波纹方向的抵抗面外弯曲能力有所下降[7]。

3) 从最大位移发生位置来看，2个模型最大位移均发生在宽度较大的波纹板7和平板中部位置，除了考虑平板抗弯刚度较小之外，还考虑到波纹板宽度对其抗弯刚度的影响，说明相同波高的波纹板随着跨距数增多，其抗失稳和破坏能力越弱。

4) 最大应力和最大位移均发生在泥浆罐侧壁的中部位置，说明侧壁在液体晃动作用下具有近似简支梁在均布载荷下的受力状态，即跨中位置处所受弯矩最大，这是进行泥浆罐侧壁设计分析中应重点关注的区域。

以最大Von-mises应力即波浪入射方向90°工况为例，模型1和模型2应力云图如图5所示。

为了定量分析并对比液体晃动对泥浆罐侧壁强度和刚度的影响，引入强度裕量削减系数和刚度裕量削减系数,即

图5 90°入射方向TLP泥浆罐侧壁Von-mises应力云图Fig .5 Von-mises stress contour plot of mud tank wall (90° wave direction) of TLP

(i=0°,45°,…,315°；j=1,2,…,10)

(3)

(i=0°,45°,…,315°；j=1,2,…,10)

(4)

式(3)、(4)中：γij为波浪入射方向为i时板j的强度裕量削减系数；σs为泥浆罐侧壁许用应力， MPa；σ1j为模型1中板j最大Von-mises应力， MPa；σ2ij为模型2在波浪入射方向为i时，板j最大Von-mises应力， MPa；ηij表示波浪入射方向为i时，板j的刚度裕量削减系数；ss为侧壁允许位移， mm；s1j为模型1中板j最大位移， mm；s2ij为模型2在波浪入射方向为i时板j最大位移， mm。s1j与s2ij的绝对值均在0～1之间，其绝对值反映液体晃动对泥浆罐侧壁应力和变形的影响，越接近于1说明影响越大，即泥浆罐侧壁对TLP 6个方向自由度的运动越敏感，反之则越不敏感。

计算8个方向、10个泥浆罐侧壁板材强度裕量削减系数如图6所示，刚度裕量削减系数如图7所示。

图6 TLP泥浆罐侧壁强度裕量削减系数Fig .6 Strength allowance reduction factor of mud tank wall of TLP

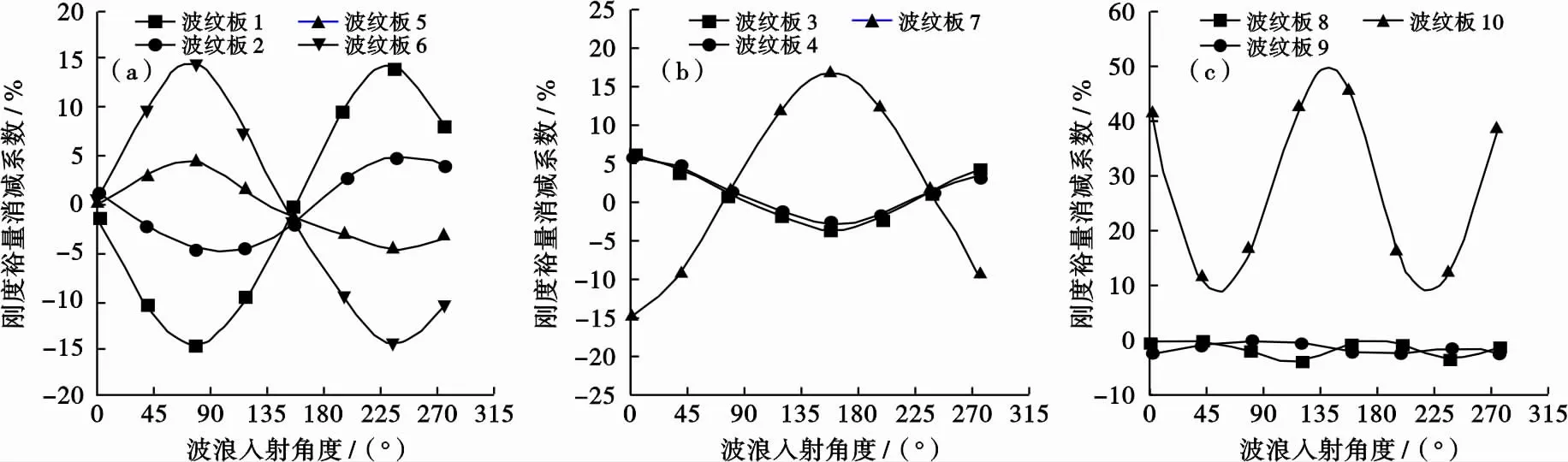
图7 TLP泥浆罐侧壁刚度裕量削减系数Fig .7 Stiffness allowance reduction factor of mud tank wall of TLP

由图6a、b可知：一方面，惯性载荷作用下使得泥浆罐外侧壁应力重新分布，不同方向的外侧壁板应力变化存在一定差异，同一方向的外侧壁板强度裕量削减系数随波浪入射角度呈周期性变化，波纹板法线方向与波浪入射方向夹角越小,垂直方向强度裕量削减系数绝对值越大，反之则越小，说明液体晃动对泥浆罐侧壁应力的影响受波浪方向的制约，因此，在进行TLP泥浆罐外壁板结构设计时，应根据平台所在海域波浪长期分布对各方向的外壁板进行综合统计分析；另一方面，各波浪入射角度下泥浆罐外壁波纹板强度裕量削减系数幅值均较小，宽度较大的波纹板1、6和7的强度裕量削减系数幅值大于其他波纹板，说明液体晃动对波纹板外壁应力影响很小，这是由于波纹板具有较强的抗弯刚度且抗弯刚度随波纹板跨距数的增大而减小[9]。由图6c可知，绝大部分波浪入射角度下的波纹板内壁强度裕量削减系数小于零，但平板内壁应力较静水压模型有所增加，说明在惯性载荷作用下泥浆罐波纹板内壁可以将应力有效地传递给波纹板外壁，使得内部波纹板侧壁应力反而小于静水压模型，而平板内壁不具有此性质。

由图7a、b可知：由于泥浆罐内部液体粘滞阻尼的影响[10]，不同方向的外侧壁板变形变化存在一定差异，泥浆罐外侧壁刚度裕量削减系数与强度裕量削减系数随波浪入射角度的变化趋势相似，但各角度下的刚度裕量削减系数幅值较强度裕量削减系数有明显增加，说明液体晃动对泥浆罐外壁位移影响更加明显。由图7c可知，各波浪入射角度下平板内壁刚度裕量削减系数均远大于波纹板且均为正值，说明液体晃动对平板侧壁变形影响较大，即平板变形对TLP六个自由度运动的运动极为敏感，因此，在进行TLP泥浆罐结构设计时应重点关注其内部平板侧壁，在不影响工艺的前提下可考虑对其进行优化。

4 结论与建议

1) 液体晃动下，TLP泥浆罐侧壁最大应力和最大变形均发生在板材中部位置，受力状态近似于均布载荷作用下的简支梁，因此在进行TLP泥浆罐结构设计时应重点关注该位置处的受力和变形。

2) TLP泥浆罐外侧壁刚度裕量削减系数与强度裕量削减系数随波浪入射角度均呈现相似的周期性变化，因此在进行TLP泥浆罐外壁板结构设计时应根据平台所在海域波浪长期分布对各方向的外壁板进行综合统计分析。

3) 液体晃动虽对TLP泥浆罐侧壁应力影响较小，但会极大程度增大内部平板的变形，因此在进行TLP泥浆罐侧壁结构设计时应考虑对其内部平板进行优化，在不影响内部工艺的条件下可考虑将其更换为波纹板。

[1] 屈博志,李玉田.生产储油平台储罐液体晃动分析[J].中国新技术新产品,2010(7):24-25.QU Bozhi,LI Yutian.Analysis of liquid sloshing of storage tank on production storage platform[J].China New Technologies and Products,2010(7):24-25.

[2] 刘刚.海洋平台储油罐安全可靠性及优化设计[D].青岛：中国石油大学(华东),2013.LIU Gang.Safety reliability research and optimization design of platform with oil storage tank[D].Qingdao:China University of Petroleum,2013.

[3] 周国发,孙丽娜.基于流固耦合作用的罐式集装箱强度分析[J].南昌大学学报(工科版),2012,34(2):111-114.ZHOU Guofa,SUN Lina.Strength analysis of tank truck based on fluid-structure interaction[J].Journal of Nanchang University (Engineering&Technology),2012,34(2):111-114.

[4] ELLIS N.A tension leg floating platform[R]∥Case Histories in Offshore Engineering.Springer Vienna,1985:167-205.

[5] TABESHPOUR M R,GOLAFSHANI A A,SEIF M S.Comprehensive study on the results of tension leg platform responses in random sea[J].Journal of Zhejiang University-Science A,2006,7(8):1305-1317.

[6] 黄祥鹿,陆鑫森.海洋工程流体力学及结构动力响应[M].上海：上海交通大学出版社,1992.

[7] HAVELOCK T H.The damping of the heaving and pitching motion of a ship[J].The London,Edinburgh,and Dublin Philosophical Magazine and Journal of Science,1942,33(224):666-673.

[8] American Petroleum Institute.Recommended practice for planning,designing and constructing fixed offshore platforms:working stress design:upstream segment[S].2012.

[9] 郭彦林,张庆林.波折腹板工形构件截面承载力设计方法[J].建筑科学与工程学报,2006,23(4):58-63.GUO Yanlin,ZHANG Qinglin.Design method of section bearing capacity of I type member of corrugated web[J].Journal of Architecture and Civil Engineering,2006,23(4):58-63.

[10] ZOU C F,WANG D Y,CAI Z H,et al.The effect of liquid viscosity on sloshing characteristics[J].Journal of Marine Science and Technology,2015,20(4):765-775.