基于Matlab/Simulink的汽车制动防抱死研究

蒙 柳 Meng Liu



基于Matlab/Simulink的汽车制动防抱死研究

蒙 柳 Meng Liu

（陕西法士特齿轮有限责任公司 实验中心，陕西 西安 710117）

汽车制动距离的大小主要与地面制动力、制动器制动力与附着力存在关系，而制动过程中控制滑移率在15%～20%时，车辆可获得较好的地面附着力，从而缩短并改善汽车在制动时出现的制动距离过长以及发生侧滑跑偏造成交通事故。利用Matlab/Simulink仿真软件模拟车辆在行驶过程中有无防抱死制动系统时的制动性能，验证利用ABS控制车辆制动时的滑移率在15%～20%具有较好的制动效果。

制动距离；侧滑跑偏；滑移率；Matlab/Simulink仿真

0 引 言

汽车制动性是汽车的主要性能之一，制动性直接关系到交通安全，重大交通事故往往与制动距离太长、紧急制动时发生侧滑等情况相关，因此汽车的制动性是汽车安全行驶的重要保障[1]。

根据地面制动力、制动器制动力与附着力之间的关系，汽车地面制动力首先取决于制动器制动力，同时又受到地面附着条件的限制，因此只有汽车具有足够的制动器制动力，同时地面又能提供高的附着力时，才能获得足够的地面制动力。

利用Matlab/Simulink仿真软件建立相应的防抱死ABS制动系统模型来验证汽车制动性能，在防抱死制动系统作用下制动距离、滑移率以及制动时间的仿真验证与不具有ABS制动系统模型相比对，具有ABS制动系统的汽车在制动过程中具有良好的制动效果。

1 车轮制动模型

不考虑空气阻力、车轮滚动阻力及加速阻力等因素，只考虑车体纵向运动和车轮转动，可得2自由度模型如式（1）～（3）[2]，车轮制动受力情况如图1所示。

车辆运动方程

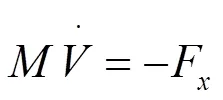
车轮纵向摩擦力

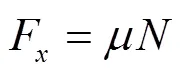
式中，M为汽车的质量，kg；V为汽车的速度，m/s；Fx为地面制动力，N；I为车轮转动惯量，kg×m2；w为车轮角速度，rad/s；r为车轮滚动半径，m；Tb为制动力矩，N×m；Tg为轮胎和地面的制动力矩，N×m；m为附着系数；N为车轮对地面法向反力，N。

2 构建制动仿真模型

2.1 车辆行驶滑移率

当车轮处于制动状态时，车轮受到摩擦片与制动器相互摩擦产生的制动器制动力并引起轮胎与路面摩擦产生地面制动力，车轮的轮速在不断下降，并出现滑移；随着制动压力的增加，车轮滑移的成分也在不断增加，当制动器制动力大于路面附着能力极限时，车轮会出现抱死并产生拖滑现象。

在地面制动力和制动器制动力矩的共同作用下，车轮的转速下降从而改变滑移率，滑移率的改变又导致地面制动力的变化[3]。经过试验得出，当车轮的滑移率或制动减速度在某个范围内变化时，汽车可获得良好的制动效果，有效防止发生侧滑现象以及缩短制动距离。

车轮制动时的滑移一般采用来描述[4-6]，滑移率和纵向附着系数以及侧向附着系数的关系如图2所示。

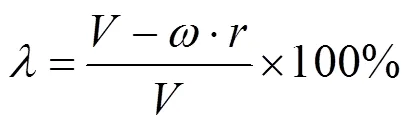
式中，l为车轮的滑移率；V为整车速度，m/s；w为车轮的转动角速度，rad/s。

2.2 防抱死制动系统建模

汽车未制动之前，车轮转动时的初始角速度应与车辆的速度相对应。仿真模型中采用2个模块来分别计算车轮角速度与车速。利用2个速度来计算滑移率，其由公式（5）来表示。

没有滑移时车轮角速度

式中，v为车轮半径划分的车辆角速度，rad/s；v为车辆线速度，m/s；r为车轮半径，m；w为车轮角速度，rad/s；为滑移率。

滑移率为0时，车轮速度与车速相等；当车轮抱死时滑移率为1。由图2知理想的滑移率应控制在15%～20%之间，即车轮转速在数值上等于0.8倍非制动条件下与其车速相同的车轮转速。从而最大限度地减少轮胎和路面之间的附着性，并最大限度地利用摩擦力矩减小制动距离。

轮胎与路面之间的摩擦系数u为滑移率的一个经验函数，即滑移率曲线。通过Matlab中变量使用Simulink框图建立滑移率曲线，该模型的摩擦力f为轮胎垂向作用力与摩擦系数u的乘积，作用于轮胎的周缘。滚动阻力除去车身质量得到车辆减速度，并通过积分获得车辆的速度[7]，防抱死制动系统车轮速度模型如图3所示。

该模型根据实际的滑移和所需的滑移之间的误差采用一个理想的鲁棒防抱死制动控制器，为使制动距离最小化则使滑移率的值控制在接近滑移率曲线的峰值，一般出现在滑移率为15%～20%。防抱死制动系统模型如图4所示。

图3 防抱死制动系统车轮速度模型

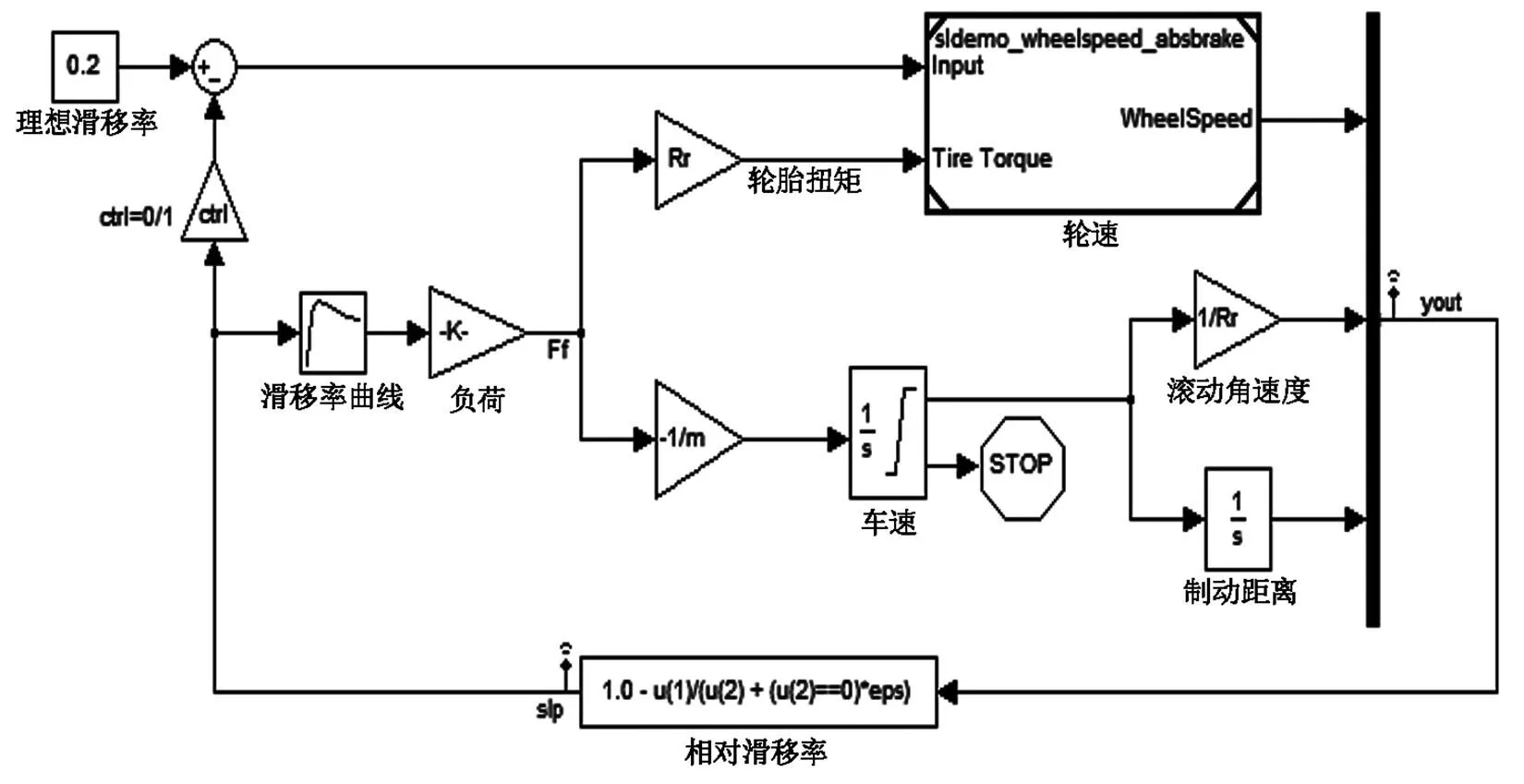
图4 防抱死制动系统模型

由于在实际车辆行驶过程中，滑移率是不能直接测量获得的，所以此控制几何算法是不实际的。

控制制动压力的变化率，模型从实际滑动减去期望滑动并将信号转化为Bang-Bang控制（+ 1或-1，取决于正负误差）；这个开/关速率通过1阶滞后表示与制动系统的液压管路相关联的延迟；该模型集成过滤率，以产生实际的制动压力，由此产生的信号乘以制动活塞面积和半径相对于车轮制动力矩系数。

3 仿真结果验证

3.1 具有防抱死制动系统的仿真

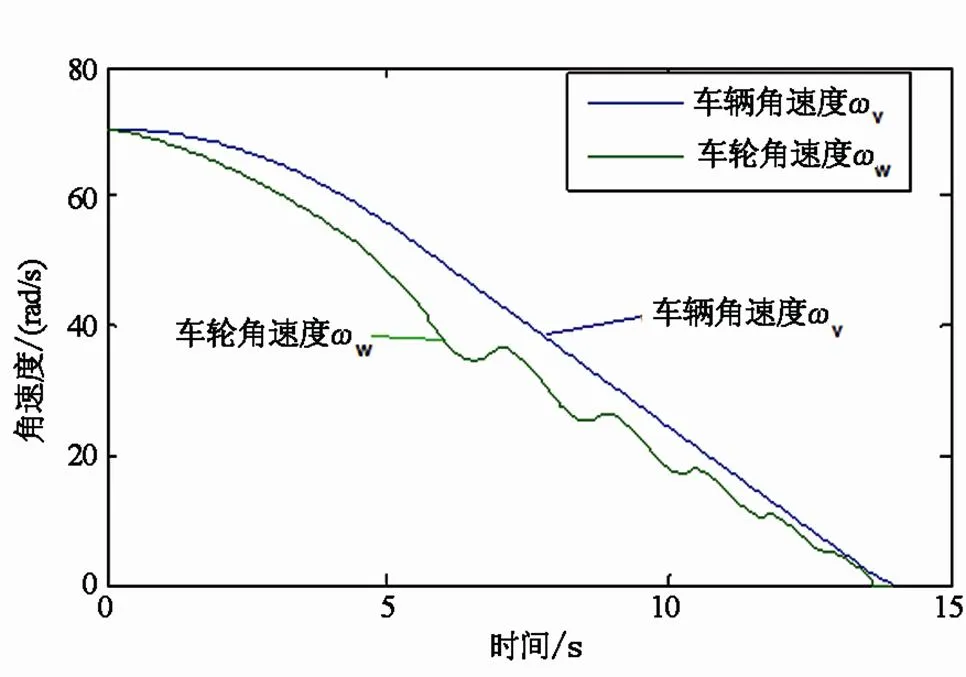
图5 具有防抱死制动系统的车辆与车轮速度

防抱死制动系统模型的仿真结果如图5～6所示，车轮角速度与车辆角速度对应，在车轮没有抱死制动的情况下车轮速度始终低于车身速度，车辆行驶速度由70 km/h降至0 km/h的时间低于15 s；并且在制动过程中滑移率能够保持在20%左右。

图6 具有防抱死制动系统的滑移率仿真结果

3.2 没有防抱死制动系统的仿真

图7 没有防抱死制动系统的车辆与车轮速度

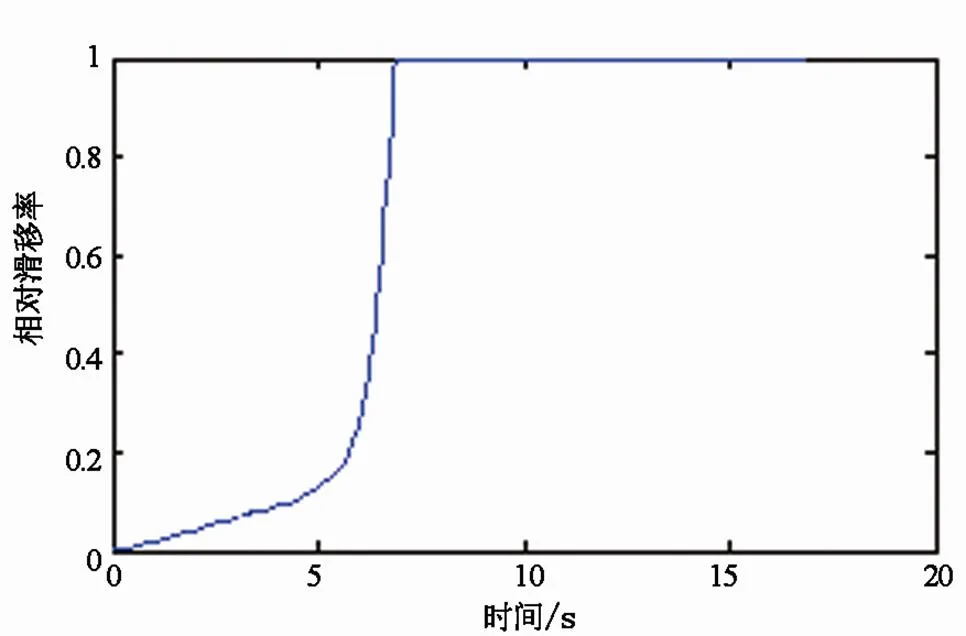
图8 没有防抱死制动系统的滑移率仿真结果

不具有防抱死制动系统的模型仿真结果如图7～8所示，车轮在第7 s左右抱死，当车轮抱死之后可以利用的地面附着力瞬间下降，车辆滑移率急剧变为1作纯滑动；车辆行驶速度由70 km/h降至0 km/h的时间超过16 s。

3.3 制动距离

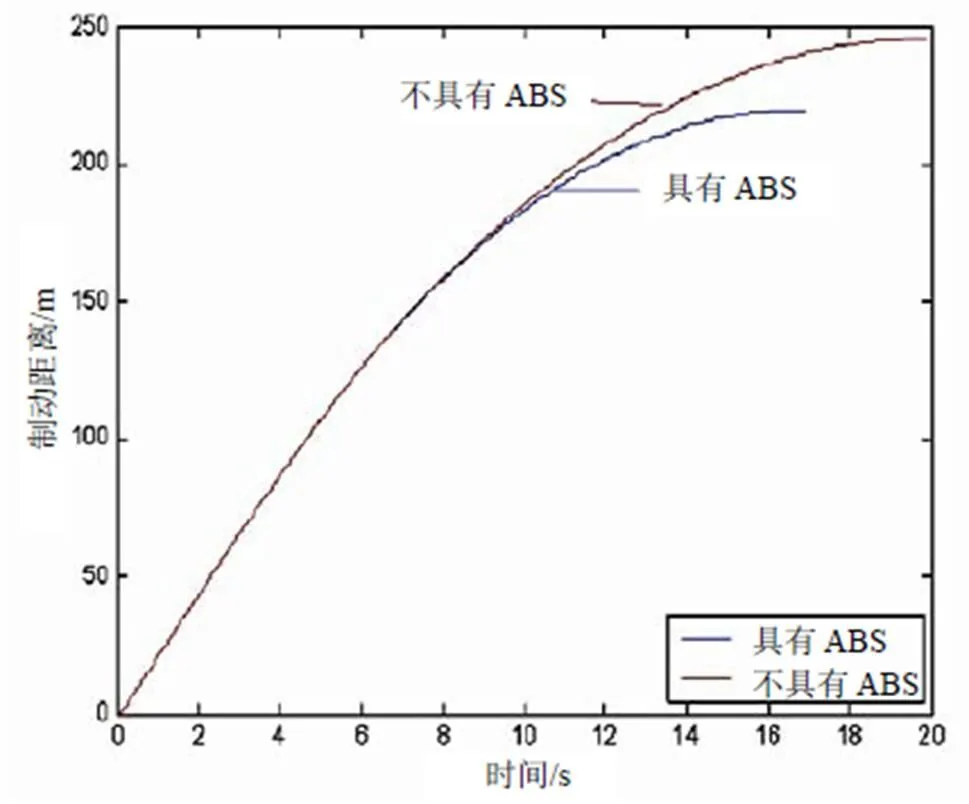
图9 车辆制动距离仿真结果

根据图9中车辆制动距离仿真结果显示，不具有ABS的车辆制动距离比具有ABS的车辆制动距离超出40 m左右，制动时间超出3 s。

4 结 论

1）基于Matlab/Simulink以及汽车动力学相关理论建立汽车纵向动力学模型，仿真得到车速及汽车前、后轴垂直力。

2）搭建与所得车速及前、后轴垂直力相应的轮胎模型，并详细阐述轮胎滑移速度模型、接触点滑移模型以及低速下滑移率修正模型等子模型。

3）汽车纵向动力学模型与轮胎模型相互关联，是整个汽车模型中的关键部分。通过Matlab/ Simulink建立的轮胎模型能够对不同状态下的轮胎滑移状态进行研究，具有一定的理论参考价值。

[1]余志生. 汽车理论[M]. 北京：机械工业出版社，2009.

[2] Thomas D. Gillespi. 车辆动力学基础[M]. 北京：清华大学出版社，2006.

[3]侯光钰. 车辆防抱死制动系统的控制技术研究[D]. 南京：东南大学，2005.

[4]许男. 复合工况下轮胎稳态模型研究[D]. 长春：吉林大学，2012.

[5]E. Bakker，H. B. Pacejka，L. Nyborg. Tyre Modeling for Use in Vehicle Dynamics Studies [J]. SAE paper，1987.

[6]H. J. Hong，H. Y. Jo. Prediction of Friction Between Tire and Road Using Powertrain Model [J]. Proc. Advanced Vehicle Control，1998：135-140.

[7] Chankyu Lee，Karl Hedrick，Kyongsu Yi. Real-time Slip-based Estimation of Maximum Tire-road Friction Coefficient [J]. IEEE/ASME Transactions On Mechatronics，1960，9（2）：454-458.

2017-11-02

U463.5：TP391.9

A

1002-4581（2018）01-0043-04

10.14175/j.issn.1002-4581.2018.01.012