渗透思想方法 提高数学素养——以“鸡兔同笼”问题的教学为例

安徽太和县第三小学（236600） 王国才

《义务教育数学课程标准》（实验稿）在总体目标中指出：“通过义务教育阶段的数学学习，使学生能够获得适应未来社会生活和进一步发展所必需的数学知识以及基本的数学思想方法和必要的技能。”《义务教育数学课程标准（2011年版）》将数学思想方法作为“四基”之一，充分说明了在数学教学中渗透数学思想方法的重要性。因此，教师只有领悟教材中蕴含的数学思想，才能从整体上、本质上理解教材，才能科学、灵活地设计教学方案，提高学生的数学素养。如果说数学知识是写在教材上的一条明线，那么数学思想方法就是隐含其中的一条暗线。明线容易理解，暗线不易看清。正是由于数学思想方法具有内隐的特性，导致许多教师在平时的教学中常忽视它的存在。

一、忽视渗透数学思想方法的原因

1.认识模糊

东北师范大学资深教授史宁中说：“数学教学的最终目标，是要让学习者会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。”数学的眼光对应抽象，数学的思维对应推理，数学的语言对应模型，它们是数学思想方法的三个要素。可见，数学思想方法在整个小学数学学习阶段是非常重要的。但是通过调查发现，部分教师从未在课堂教学中渗透过数学思想方法，尤其是年龄较大的教师，他们对数学思想方法的认识不深，只注重知识与技能的传授，忽视数学思想方法的渗透，这是一种强制性的“给予”。

2.能力欠佳

美国颇有影响力的教师雷夫说：“我不是教课的，我是教人的。”也就是说，要从课程的深处、从教材的背后、从教学的背后，看到学生的存在，关注学生的素养。有些教师独立钻研教材的能力不强，挖掘教材中隐含的数学思想方法的能力欠佳，因而忽略了其中蕴含的数学思想方法。长此以往，将导致学生所学的数学知识呈现孤立的、零散的状态，不利于学生构建知识体系，同时也不利于学生内化数学思想方法，阻碍了学生数学素养的提升。

3.引领不够

部分教师参加学习培训的机会不是很多，最关键的是教师学习的自觉性不高。此外，有的学校教研活动的开展流于形式，没有针对性和实效性，缺少专家或名师的指点，导致数学教师对新理念、新方法的认识不足。

二、探寻数学思想方法的渗透策略

多年的教学实践使我深刻地认识到，数学教学不应该仅仅是数学知识的教学，还应该是渗透数学思想、培养思维能力的教学。教师的作用在于帮助学生通过一系列的活动去“做数学”，实现数学的“再创造”。作为小学数学教师，不仅要教给学生数学知识，还要向学生渗透知识中蕴含的思想方法。如果将数学思想方法置于与知识技能同等的地位，那么培养学生的核心素养才不会是一句空话。为此，我对“鸡兔同笼”一课进行了细致的分析，旨在挖掘教材中隐含的数学思想方法。

1.课前思考

“鸡兔同笼”问题，单从知识的角度、从实际的生活中去探究并没有重要的意义，有谁会把鸡和兔子放在一个笼子里养呢？生活中很少有这样的事例，那为什么还要研究它呢？这就要求教师形成清晰的认知：本节课主要是以“鸡兔同笼”问题为载体，让学生初步体会运用假设的数学思想方法解决问题的过程，同时为七年级学习利用一元一次方程中的代入消元法、加减消元法将两个未知数转化成一个未知数做铺垫。

2.教学环节

（1）故事导入，渗透转化思想

师：同学们，你们知道《曹冲称象》的故事吗？谁愿意讲给大家听呢？

（学生讲故事）

师：在这个故事中，曹冲不但聪明，而且非常勇敢。他在遇到难题时善于开动脑筋，想到把称大象的重量转化成称石头的重量，并在那么多人的面前勇敢地提出自己与众不同的想法，这种精神值得大家学习。转化在数学中的应用有很多，今天老师就带领大家学习运用转化的方法来解决问题。

以历史故事引入，既激发了学生的学习欲望和学习积极性，又为转化思想方法的教学做了铺垫。

（2）化难为易，渗透简化思想

师（出示教材《孙子算经》中的趣题：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”）：你能说一说这道题是什么意思吗？

（学生尝试解释题目的意思）

师：这道题的意思是，有若干只鸡和兔放在同一个笼子里，从上面数，有35个头；从下面数，有94只脚，请问笼中各有鸡和兔几只？

师：为了方便同学们研究问题，我们先来研究一个数据较小的“鸡兔同笼”问题。笼子里有若干只鸡和兔，从上面数，有9个头，从下面数，有26只脚，求鸡和兔各有几只。

简化问题，先研究小的方面，然后以小见大，能使学生的思考方向更明确、思路更清晰。这种设计既给数学课堂带来了浓厚的文化气息，又渗透了简化的思想方法，易于学生从简单入手、化难为易、发现规律，从而获得解决问题的方法。

（3）画图或逐一列表，渗透数形结合思想

师：我们画圆当作动物的头，画线段当作动物的腿。先画出9个圆。假设这9只动物全是鸡，并给每只鸡画上2条腿（如下图所示）。

师：画完后数一数，发现只有18条腿，和题目中说的26条腿相差8条，这是因为我们把兔子都看作了鸡。这时把剩下的8条腿2条2条地添到刚刚画出的“鸡”上（如下图），一共可以添4只，说明笼子中有一共有4只兔子。

师：所以鸡有5只，兔有4只。

师：这个问题还可以用逐一列表法来解答。先假设有1只鸡、8只兔，那么腿一共有34条，比26条多，不符合条件，接着假设有2只鸡、7只兔，腿一共有32条，也不符合条件，那么继续假设，直到找到符合条件的答案为止。

（发放表格；学生填表，教师巡视，对学习有困难的学生给予帮助）

生：

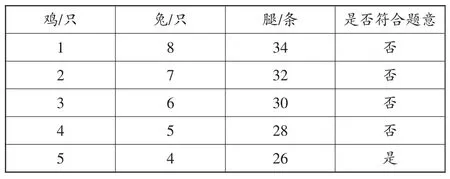
著名数学家华罗庚指出:“数无形时少直观，形无数时难入微。”在这一教学环节中我借助数形结合思想中的图形直观手段，巧妙地运用画图法、列表法，为学生提供非常直观的数学素材，把抽象的鸡兔同笼问题转化成学生易于理解的问题，既拓宽了学生的思路、留给学生思考的空间，又让学生在解决问题的过程中发现列表的作用，为建构新知奠定基础。这样不仅使学生能非常清楚地明白“鸡兔各有几只”的复杂问题，而且让学生通过观察图形和表格，获得解题的思路和方法，从而掌握其中的数学思想。

（4）列表法，渗透优化的数学思想方法

师：刚才我们用逐一列表的方法解决了“鸡兔同笼”问题，但是逐一列举只适用解决数量较小的“鸡兔同笼”问题，如果鸡和兔的数量很大，用这种方法解决就会非常慢且麻烦，对此我们不妨探究“跳跃列表”和“折中列表”两种方法。

师：根据第一次假设的数据与实际数据的差距，可“跳跃”着选择数据。这种方法在一定程度上能加快寻找答案的速度。

师：先假设中间的数据，再根据结果判断是向前还是向后寻找。

运用多种方法解决“鸡兔同笼”问题，目的是让学生了解算法的多样性，启迪学生的发散思维和创造性思维，让学生在探究解法的过程中，经历“猜测—验证—调整—再验证—再调整”的过程，在不断调整数据中发现快速寻找答案的方法。这些过程均渗透了“优化”的数学思想方法。

教学实践证明，所学到的知识在进入社会后经过一段时间也许就会被学生遗忘，然而那些铭刻于头脑中的思想方法却长期地在他们的生活和工作中发挥着作用。由此可见思想方法是知识的灵魂和精髓，掌握数学思想方法对提升学生的思维品质，乃至对学生的终身发展都具有十分重要的意义。因此，在教学设计中，教师要追本溯源，让学生亲身经历知识的探索过程，并运用观察与实验、抽象与概括、类比、归纳、转化等方法，逐步渗透数形结合、分类讨论、化归与转化、优化与简化等数学思想，让学生学到具有生命力和生长性的知识。古语有云：“授之以鱼不如授之以渔。”一个掌握了研究方法的人，比一个纯粹的“知识的集大成者”更会学习、更享受学习，也更能适应未来学习型社会的发展需要。在教学过程中不断向学生渗透数学思想方法，拓宽学生的思维通道，才能促进学生数学素养的不断提升。