全捷联激光制导弹药双透镜滚转角测量方法

刘振亚,高 敏

(陆军工程大学导弹工程系,河北 石家庄 050003)

1 引 言

激光制导弹药是指利用激光探测得到目标信息以及弹体运动信息,形成制导指令,使控制系统实时调整弹体的飞行弹道,直至准确命中目标的一种精确打击武器[1]。相比于俯仰角以及偏航角在弹丸飞行过程中的变化,滚转角变化显著；并且其在判断执行机构空间位置,确定执行机构起控时刻以及全捷联弹目视线角解耦等制导控制环节都起到了至关重要的作用。因此,滚转角也是弹丸姿态测量中最为重要的信息[2]。

滚转角测量方法有许多,但为满足制导弹药抗高过载、低成本、小型化的作战需求,目前主要应用的有太阳方位传感器法、微机电系统(MEMS)陀螺仪、卫星定位、地磁测量以及组合导航等方法[3-6]。其中,太阳方位传感器法易受外界干扰,MEMS陀螺仪精度受环境影响较大且具有积累误差,卫星定位系统所需空间较大,地磁测量精度不高。针对原有滚转角探测方法的不足以及局限性,国内外专家学者提出了利用探测器接收信息作为基准对弹体滚转角进行精确测量:卜彦龙等[7]通过分析目标相对于导引头的成像规律,推导出图像反旋公式,实现了自选角速度的实时跟踪。Han等[8]在单体周围均匀布置多个激光敏感器,利用激光束照射得到滚转角。李兴隆等[9]将滚转角零位测得的体视线角作为惯性基准,利用弹载GPS组件结合捷联探测器量测信息得到弹丸滚转角。

上述利用探测器接受信息对弹丸滚转角测量的方法虽然具有一定的干扰能力且精度较高,但多个敏感器或GPS接收装置不仅增加了导引头体积,并且成本较高。本文针对上述问题,将滚转角零位测得的体视线角作为惯性基准,设计了一种全捷联激光半主动弹药双透镜滚转角测量方法。

2 导引头数学模型建立

激光半主动制导技术是应用激光发射器向目标发射一定频率的激光,光线经目标漫反射后由制导弹药导引头内的激光探测器接收,根据接收光斑坐标解算得到弹目相对运动信息,导引头数学模型如图1所示。

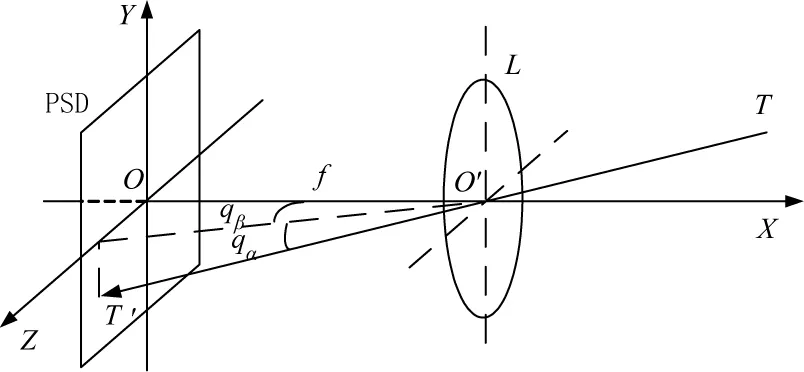
图1 导引头模型

其中,坐标系O-XYZ为弹体坐标系,O为激光位移敏感探测器中心,且位于透镜的焦点处以保证得到清晰的光斑。OX轴沿弹轴方向,OYZ平面为PSD平面,OY轴在弹体纵向对称面且与弹体轴向垂直,OZ轴根据右手法则与平面OXY平面垂直指向右方。L为光学透镜,其中心O′与弹轴重合,焦距为f。由于透镜中心距离弹体质心位置相对于弹目距离可以忽略,因此,设透镜中心位置为弹体质心位置,其在惯性系下的坐标为(xg,yg,zg)。T为目标点,设其在惯性系下的坐标为(xt,yt,zt),T′为目标点经激光反射在PSD上形成的光斑,设其在弹体坐标系下的坐标为(0,ya,za)。TT′为弹目视线,其与弹轴夹角在OXZ平面的夹角为体视线倾角qα,在OXZ平面的投影为体视线偏角qβ。

弹目视线TT′在惯性系下的坐标为(xg-xt,yg-yt,zg-zt),设其在弹体系下的坐标为(x1,y1,z1),根据坐标系转换关系可得到弹目视线在惯性系下与弹体系下的坐标转换关系:

(1)

其中,φ为弹体俯仰角;ψ为弹体偏航角;γ为弹体滚转角。根据弹体系下TT′的坐标,可得到体视线倾角与体视线偏角:

(2)

如图1所示,根据激光在PSD上成像原理,可以得到光斑在PSD内的坐标:

(3)

利用PSD上接收到的激光光斑信号,根据上述建立的导引头模型即可得到目标点相对于弹体的位置信息。

3 双透镜滚转角测量原理

双透镜测量系统主要由两个相同的光学透镜与激光探测器组成,其中由于双透镜测量方法需要在探测器平面形成两个光斑,而单光敏面PSD器件只能探测单个光斑,因此选择二维PSD阵列作为激光探测器,其原理如图2所示。透镜L1中心与弹轴重合,且其焦点在PSD平面上；透镜L2的焦点也在PSD平面上,其中心与L1中心连线l与OZ轴平行且沿其轴正向。制导弹药导引头所接收的为激光照射目标所形成的漫反射光束,由于透镜间距离l相对于弹目距离可以忽略不计,因此两透镜所接收的光束可近似看作平行光束。一般旋转稳定弹药的滚转角速度相对于俯仰、偏航角速度以及弹目视线角速度较大,在一个滚转周期内可近似看作弹体只绕OX轴做滚转运动。当弹体绕OX轴滚转时,由于弹目视线近似不动,而PSD与弹体固连,透镜L1在PSD形成绕O点做圆周运动的光斑轨迹；而由于透镜L2与PSD按照相同的滚转角速度绕OX轴运动,因此透过透镜L2的光束在PSD平面上形成的光斑始终为固定点B。下面证明此固定点即为滚转角为0°时,弹目视线在PSD上形成的坐标点。

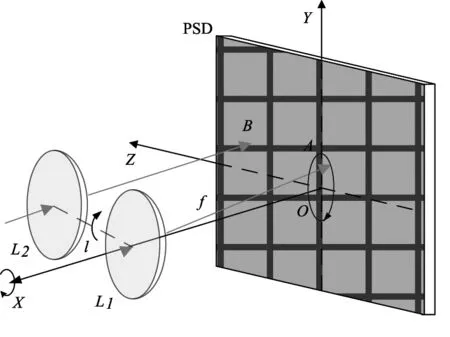
图2 双透镜测角结构

通过上述讨论可知,平行光束经过透镜形成的光斑坐标B与滚转角度不相关,可得过L2光束在弹体系下的坐标(x2,y2,z2)的表达式:

(4)

对比式(1)和式(4),当透镜L2位于OZ轴正向时,过L2的光束在弹体系下的坐标B始终为滚转角0°延L1L2方向平移l的坐标。而这时影响平行光束在PSD上形成的光斑坐标A与B相对位置的因素仅由滚转角γ决定,即坐标A相对于B在单位时间内转过的角度为Δγ。利用B为滚转角0°时弹目视线在PSD上坐标的特点,可将其作为空中姿态对准基准,利用A与B的相对位置关系得到弹体滚转角:

γ=α2-α1

(5)

其中,α1和α2分别为过两透镜L1、L2平行光线在PSD平面投影与Z轴的夹角。

4 精度影响因素分析

4.1 测量原理误差

在进行推导滚转角测量方法时,由于弹目相对距离较远,将导引头接收的激光束视为平行光。但在弹丸实际飞行过程中,导引头内经过透镜L1与L2的激光束相对位置如图3所示。

图3 实际光束相对位置

其中,激光束过透镜L1在PSD 平面形成光斑A,平行光束过透镜L2在PSD上形成光斑B,实际弹体接收光束在PSD上形成光斑B′,两束光线夹角为δ。当两光束夹角增大时,利用光斑坐标求解滚转角的误差也随之增大。利用两不平行光束矢量及余弦定理可得δ的表达式:

L2B′=L2B+l(sinφcosψsinγ+sinψcosγ-

cosφsinγ-sinφsinψsinγ+cosψcosγ

(6)

其中,L2B与L2B′分别为不平行两光束在惯性系下的矢量。由式(6)可以看出,影响两光束平行度的因素为透镜间距离l以及弹体姿态角,而弹体姿态角不可改变。因此,设计导引头时,在满足视场要求的前提下,尽可能地减小两透镜间的距离,从而增加经过两透镜光束间的平行度,减小滚转角测量误差。

4.2 PSD量测误差

PSD量测误差主要是指PSD输出光斑坐标点与真实光斑坐标点之间的偏移程度,其主要是由PSD输出电信号与实际位置之间的线性关系程度决定,而PSD中央区域的线性程度要远比边缘区域的高[10]。因此,为保证PSD能够准确地测量光斑位置,需尽量将入射光照射到PSD中央区域。

4.3 PSD安装误差

4.3.1 PSD轴向安装误差

PSD探测器安装在透镜焦平面时产生的主要为角度误差ε与位置误差Δd,如图4所示。角度误差会导致入射光线不能在焦平面上汇聚,但由于PSD探测器输出光斑坐标与光强大小无关,只与光束中心位置有关,因此轴向安装产生的角度误差对于光斑位置没有影响。而实际PSD相对于理想位置产生的位移误差导致光斑在焦平面坐标系中也会产生一定的位移偏差,因此轴向安装位置误差对光斑坐标会产生误差影响。

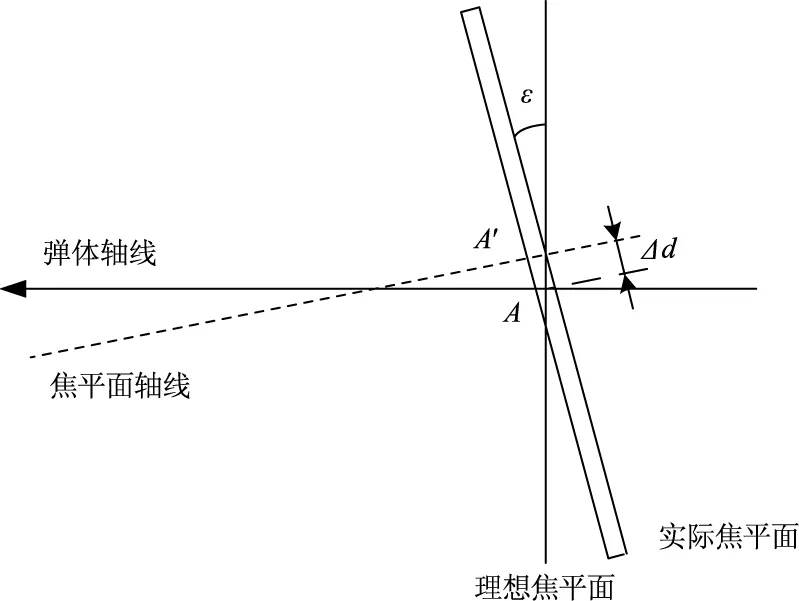
图4 轴向安装误差

4.3.2 PSD圆周方向误差

PSD圆周方向安装误差如图5所示,其中实际PSD平面绕弹轴具有安装角度误差Δγ,假设透镜L2安装无误差,则过L2光束的实际坐标相对于无圆周方向误差的坐标具有了Δγ的角度误差。因此,PSD圆周方向安装误差对滚转角测量值产生了Δγ的偏差。

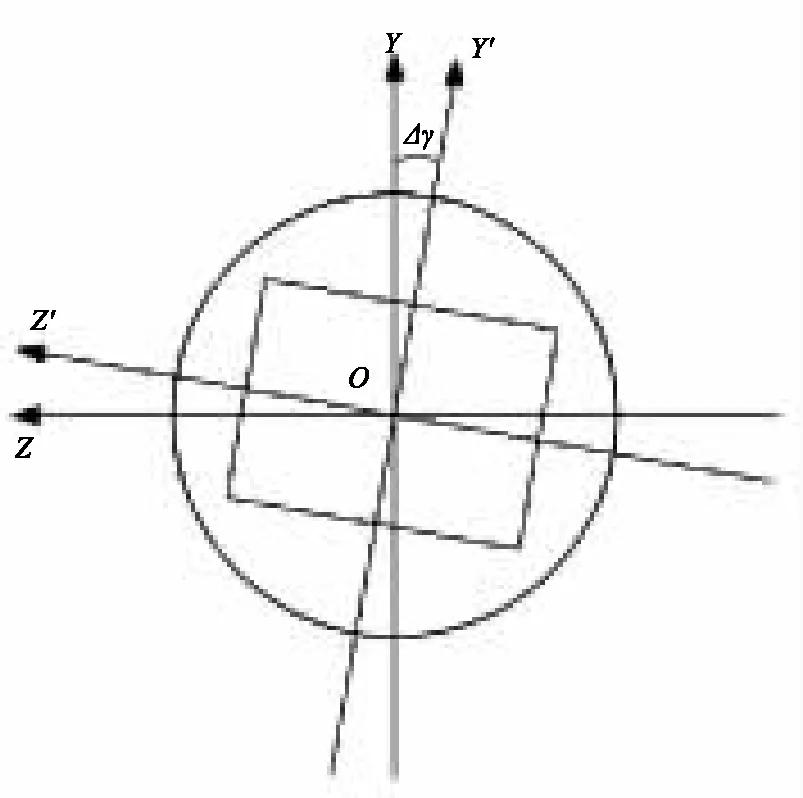
图5 圆周方向误差

5 仿真实验与分析

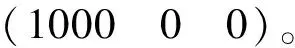
迫弹在弹道末段速度约为200 m/s,激光导引头探测距离约为2 km,因此设定导引头工作时间为10 s,实验条件如表1所示,其中,Δv/(m/s)表示初速偏差,Δangle/°表示射角偏差,Δwind表示风速偏差,ΔAwind/°表示风向偏差。利用设计好的滚转角测量方法,即可测量得到弹丸实时滚转角度,实验结果如图6与表2所示。

表1 实验扰动条件

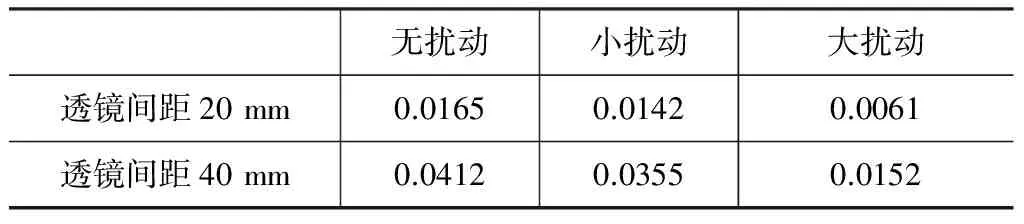
表2 不同实验环境下最大测量误差

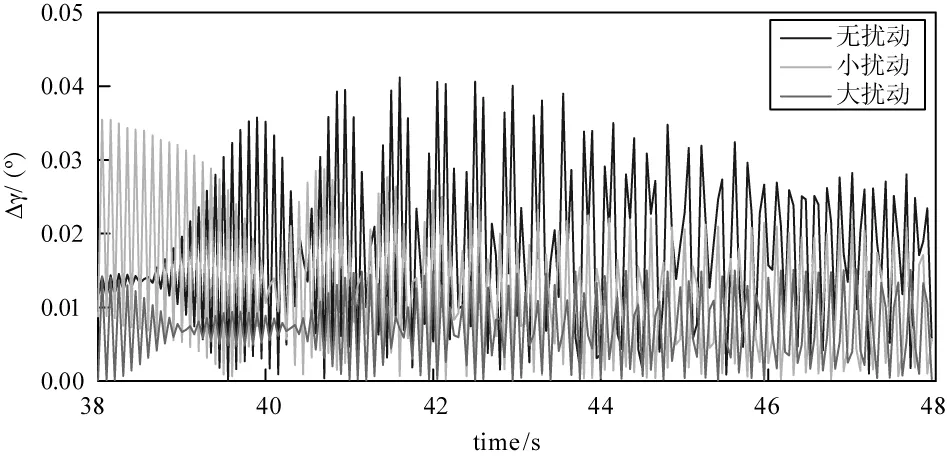
图6 滚转角绝对误差

根据实验结果可以看出,利用双透镜方法可以得到高精度弹体滚转角测量值,其精度可达到0.05°以内。在透镜间距不变时,滚转角测量误差随着扰动条件的增大而减小；在扰动条件不变时,滚转角测量误差随着透镜间距的增加而增加。通过4.1节讨论可知,双透镜测量方法原理误差是由弹体姿态角及透镜间距决定。当扰动条件增加时,导致弹丸在飞行过程中姿态角产生变化,从而导致滚转角误差产生偏差；而随着透镜间距离增加,经过两透镜光束的平行度减小,从而导致滚转角误差增大。由公式(6)可以看出,无论弹体姿态角偏差多大,透镜间距离相对于弹目距离都几乎可以忽略,因此在利用双透镜结构对弹丸滚转角可以达到高精度的测量值,从而满足弹药制导与控制的需求。

6 结 论

提出了一种利用双透镜结合PSD探测器结构的激光半主动制导弹药弹体滚转角测量方法,将滚转角为0°得到的PSD光斑位置作为基准,利用光束经过两透镜形成光斑的相对位置解算得到弹体滚转角。通过建立弹体六自由度模型对该方法进行仿真验证,表明该方法具高精度的测量值,在不同实验条件下滚转角测量最大误差在0.05°内。该方法结构简单,计算量小且精度高,为激光半主动制导弹药小型化、低成本化设计过程中提供了一定的理论依据。

[1] LIU Xuepeng.Review of semi-active laser-guided munitions homing current situation and development[J].Infrared and Laser Engineering,2010,39(S):415-419.(in Chinese)

刘学鹏.激光半主动寻的制导弹药现状与发展综述[J].红外与激光工程,2010,39(增):415-419.

[2] Shi G X,Yang S X,Su Z.Afast solution of roll angle based on single-axis MEMS gyro and geomagnetic information[C]// Control Conference(ASCC),2011 8th Asian，IEEE，2011:761-764.

[3] Leach R K.Solar reference flit roll position sensor,US,USH000746[P].1990.

[4] DONG Jinlong,MO Bo.Observerbility analysis of rocket MEMS-INS/GNSS integrated navigation system attitude in classic trajectories[J].Acta Armamentar,2014,35(6):850-856.(in Chinese)

董进龙,莫波.典型弹道下的火箭弹MEM-INS/GNSS组合导航姿态误差可观性分析[J].兵工学报,2014,35(6):850-856.

[5] WANG Chao,WANG Yongji,HUO Pengfei.Projectile roll angle measurement based on gyroscope and satellite[J].Journal of Detection & Control,2016,38(1):95-98.(in Chinese)

王超,王永骥,霍鹏飞.基于陀螺和卫星定位组合的滚转角测量方法[J].探测与控制学报,2016,38(1):95-98.

[6] Xiang C,Bu X Z,Yang B.Three different attitude measurements of spinning projectile based on magnetic sensors[J].Measurement,2014,47(1):331-340.

[7] BU Yanlong,NIU Yifeng,SHEN Lincheng.New approach to decoupling problem of imaging rotation in single channel-controlled air defense missile[J].Journal of System Simulation,2006,18(5):1164-1168.(in Chinese)

卜彦龙,牛轶峰,沈林成.单通道防空导弹导引头图像的弹旋解耦新方法[J].系统仿真学报,2006,18(5):1164-1168.

[8] HAN Yongxuan,YU Jianqiao,MEI Yuesong,et al.Roll Angle Measurement System of Guided Projectile Based on Scanning Laser Beam[C]// 2013 32ndChinese Control Conference，Xi′an，IEEE,2013:5059-5064.

[9] LI Xinglong,YAO Wenjin,ZHU Likun.Projectile roll angle measurement method of a combination of strapdown laser detactor and GPS measurement for semi-active laser terminal correction[J].Acta Armamentar,2016,37(2):279-286.(in Chinese)

李兴隆,姚文进,朱立坤,等.捷联激光探测器组合GPS测量弹丸滚转角方法[J].兵工学报,2016,37(2):279-286.

[10] SHUAI Hongjun,ZHANG Shuai,SONG Jiantao,et al.Error correction for position sensitive detector based on speckle tracking system[J].Infrared and Laser Engineering,2016,45(4):1-6.(in Chinese)

帅红俊,张帅,宋建涛,等.基于光斑跟踪系统的位敏传感器误差修正[J].红外与激光工程,2016,45(4):1-6.