欲借围棋之境 更现“指对”运算力量——从2017年北京市数学高考文理科第8题的答案之争谈起

●

(浙江师范大学教师教育学院，浙江 金华 321004)

●侯 伟

(河南师范大学附属中学，河南 新乡 453002)

欲借围棋之境更现“指对”运算力量
——从2017年北京市数学高考文理科第8题的答案之争谈起

●李怀军

(浙江师范大学教师教育学院，浙江 金华 321004)

●侯伟

(河南师范大学附属中学，河南 新乡 453002)

试题研究有利于教师探明试题本质、优化试题与促进教学.文章对2017年一道有争议的高考试题，从数学概念入手，通过解法、命题背景与意图分析，提出优化试题的方法，也从这道试题的争鸣中提出此类试题命制需要关注的角度.

试题研究；指数函数；估算；命题意图

教育部考试中心于2016年10月公布的《关于2017年普通高考考试大纲修订内容的通知》要求：“增加中华优秀传统文化的考核内容，积极培育和践行社会主义核心价值观，充分发挥高考命题的育人功能和积极导向作用.”2017年北京市数学高考文理科试题第8题就体现了这一命题思想，以中华优秀传统文化中极具代表性的围棋为背景.不过，该试题因其表述与参考答案引发了一些疑问和争议：有人认为“正确答案”应该是C；也有人认为题中“接近”一词需要严格界定；还有人提出比较尖锐的批评：要解决“最接近”的问题，所给“参考数据：lg 3≈0.48”用不上且有误导作用.这道高考试题为什么会引起诸多争议？命题者的意图是什么，以及在多大程度上能够达到？这些争议又会对以后的命题和教学有什么启示？本文尝试对这些问题进行初步探讨.

1 原题再现

( )

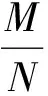
A.1038B.1053C.1073D.1093

(2017年北京市数学高考文理科试题第8题)

2 试题研究

2.1 概念界定

数学教育家波利亚曾说过：“对你所不理解的题目做出答复是愚蠢的.”这说明注意题目中的语言表述、理解题意是求解的其中一步，因此对本题中“接近”这一术语的正确理解显得尤为重要.“接近”为动词，有“靠近”与“相距不远”之意，也即是两个事物或对象之间的距离比较近[1].具体到两个实数，其“接近”程度即指二者之间的距离小或近似程度高，因此对于两个(或两个以上)正实数的“接近”程度，可以用作差或作商的方式进行表征和判断.

2.2 解法之辩

“围棋状态空间复杂度”与“宇宙中的普通物质”这两个背景元素，在表述上看似与学生的知识背景存在一定距离，但并不影响学生的理解和求解.而且，该题信息量不大，主要有“接近”和“参考数据lg 3≈0.48”两个关键信息，解题方向也比较明确.笔者对其所在学校的高中教师和部分高三学生进行访谈获知，被访谈者最常用的是解法1.

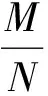
故选D.

分析2解法2对“接近”这一术语的理解和表征是正确的，而且推理形式正确，但仍然得出存在争议的答案D.分析上述的求解过程，发现解法2直接运用参考数据“lg 3≈0.48”，而没有推敲其严格性.

其实，lg 3更为精确的估计是0.477 121 25,按照这一估计，计算发现

|1092.240 771 2-1093|<|1092.240 771 2-1073|.

比如1<3<4，|3-4|<|3-1|，但是103更接近101而不是104，因为

|103-101|=990<9 000=|103-104|.

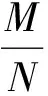
首先证明不等式

3361<5·10172.

(1)

由39=19 683,得

104<39<2·104,

(2)

从而 3360=(39)40<(2·104)40=240·10160,

所以不等式(1)可证.

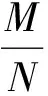
3361>(39)40>(104)40>10153,

从而

由不等式(1)可知

3361<5·10172<10173，

从而

下面作差比较：由不等式(1)可知

2·3361<10173，

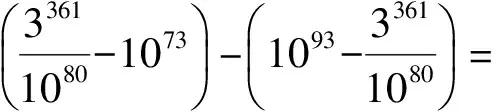
即

亦即

故选C.

分析3解法3沿用了解法2对“接近”术语的正确理解，推理过程严密，逻辑严谨，也没有使用参考数据“lg 3≈0.48”，所推导出的选项C应是正确答案.对比解法1和解法2推导出的选项D，究其原因是限制条件lg 3≈0.48的设置是否足够精确.

2.3 命题分析

因为本题是选择题，并没有呈现解答过程，所以只能根据参考答案以及上述主要的3种解法来揣测命题者的意图及其达成程度，并简要分析试题存在争议的原因.

本题命题意图主要有两个：1)以中华传统文化中极具代表性的符号为背景，从数学的视角欣赏和理解优秀传统文化的博大精深，强化爱国主义精神和民族自豪感.深入发掘中国文化内涵，讲好中国故事.2)考查学生数学阅读能力、关于对数与大数的运算能力以及估算能力.

不过，本道题中的“围棋”和“宇宙中普通物质”这两个背景元素与已知数据及求解过程没有必然联系，因此很难说第一个命题意图达成.另外，由于高考为限时考试，时间比较紧张，对于这道选择题，绝大多数考生会循着试题导向，直接使用条件lg 3≈0.48(或93.28≈93)，运用解法1(或解法2)来完成.因此，从广大考生所处的高考真实场景这一角度看，第二个命题意图在一定程度上达成.

另外，针对本题的上述争议，笔者认为：由于该题给出了确定的参考数据，因而其答案是无须争议的.但对比3种解法的求解过程可知：试题的表述与限制条件的精确性是有争议的.首先，“接近”一词是关键信息，但本题题目并没有对此作出清晰和明确的界定；其次，无论是以0.48,0.477 121 25，或其他数作为lg 3的近似值，都不应该影响试题的答案.再次，解法1先后进行了两次估算lg 3≈0.48，93.28≈93，估算前后的数值虽然相差都不大，但还原成指数幂之后，却发生了惊人的质的变化.正如解法2所呈现的：92.240 771 2仅比93小0.759 228 8，但比73大19.240 771 2，而1092.240 771 2却更接近1073.引发以上质变的根本原因是“指数”运算具有爆炸性的“放大”作用，能将细微的差别放大成显著的差异；而与此相对应的“对数”运算，却具有截然相反的缓慢性的“缩小”作用，可将上述显著的差异缩小到细微的、甚至是难以察觉的程度.

2.4 试题优化

由以上分析可知，完善本道试题可以从以下两个方面着手：1)概念的明确化与清晰化,比如借鉴2010年上海市数学高考理科试题第22题关于“远离”一词的定义，来界定本题中“接近”一词的内涵；2)进一步精确限制条件，比如给出lg 3≈0.477，或者将4个选项设置成区间的形式.

3 总结与启示

2017年北京市数学高考文理科试题第8题欲借“围棋”之境，传扬中华优秀传统文化.不过，深入探究此题，感受更多的是“指对”运算的力量.因此，对此题的相关概念进行澄清与界定，对试题进行分析和优化，有助于争论者在一定程度上消解对本道试题的疑惑与争议，也希望对数学试题命制、数学教学有一定的启发作用.

3.1 从命题者的角度看

试题表述和概念界定明确、准确、严密、不存在争议是命题之重.要想做到这一点，既要考虑日常用语通俗易懂的优点，又要发挥数学语言简洁抽象的长处，更需要注重语言表述的内在逻辑.为了简便运算，常有规定性或限制性条件的设置，但要合情合理，不能出现前后表述、题目的表层与内含信息互相“打架”的现象.另外，对“估算”的考查，最好出现在解题的最后一步或几步，即使是出现在解题过程中，也要谨慎考虑各种近似对后续运算以及解题结果的影响.

3.2 从高中数学教学的角度看

首先，要培养学生数学阅读的能力.数学是一种语言，“数学教学也就是数学语言的教学”[3].而语言的学习离不开阅读.实施数学阅读的教学，既要示范和引导学生正确感知和认读文字、数学符号、术语、公式、图表等语言符号，也要通过同化或顺应教学，将新概念纳入或重构学生的认知结构.当然，更需要与不断假设、证明、想象、推理等系列积极能动的认知过程相连贯,从而在上述阅读过程、记忆、思考等细节中提升学生的数学理解能力.

其次，树立对估算的正确认识.在教学中适时、适量渗透估算.传统对估算持有一种错误的认识，“人们在估算能力的获得上有最后时期和个体有相似的估算能力”[3].一部分中学数学教师也持有类似观点：估算能力的获得应在小学阶段完成.其实，中学阶段也需要估算，只不过这种估算是高阶的、更为复杂和抽象的，正如本道题中所体现的.估算教学应充分利用估算能力在高中时期的自然发展，同时鼓励学生在实际的数学情景中多运用估算，以尽量消除简单化和“死记硬背”的倾向.

最后，借助数学史和数学现实，促进概念教学走向知识本质.数学概念反映出数学对象的本质属性，数学研究的对象是现实世界的数量关系和空间形式，不过是被舍去具体的物质属性和关系而抽取出来的量的关系和形式构造.因此，数学概念的教学就要指向这种量的关系或形式构造的本质，借助数学史和数学现实就是两条有效的实施途径.比如，上述试题中所体现的指数与对数运算的“力量”，可以从“对数”史和“指数”的数学现实中强烈地感受到：对数运算是苏格兰数学家纳皮尔在研究天文学的过程中，为了简化其中对大数的计算而“发明”的.对数的“发明”可以将幂运算在内的乘除运算转化为加减运算，大大减小了运算量，从而缩短运算时间，使得“天文学家的寿命延长了一倍”.又可以从细胞分裂、人口增长等问题中强烈体会到，“指数爆炸”是对指数运算这一特性的形象刻画.

[1] 中国社会科学院语言研究所词典编辑室.现代汉语词典[Z].6版.北京:商务印书馆,2012.

[2] 斯托利亚尔.数学教育学[M].丁尔陞,译.北京:人民教育出版社,1984.

[3] 司继伟,张庆林.估算:来自心理学的声音[J].心理科学,2002(2):240-241.

收文日期：2017-11-22；

2017-12-24

河南省中小学学科数学教育教学研究基地资助项目

李怀军(1981-)，男，河南新乡人，博士研究生.研究方向：数学教育.

O122.6

A

1003-6407(2018)03-0024-03