水轮机活动导叶端面间隙磨蚀形态演变预测
韩 伟,陈 雨,刘 宜,魏三则,李光贤,金俊俊
水轮机活动导叶端面间隙磨蚀形态演变预测
韩 伟1,2,陈 雨1,刘 宜1,2※,魏三则3,李光贤1,金俊俊1
(1. 兰州理工大学能源与动力工程学院,兰州 730050;2. 甘肃省流体机械及系统重点实验室,兰州 730050;3. 酒泉市三元水电开发有限公司,酒泉 735000)
恒定边界条件下的磨蚀预测方法不能反映过流壁面磨蚀后流体动力学参数的变化,导致现有的磨蚀预测结果很难与实际一致。该文基于磨蚀微分求积的思想,构造了主要磨蚀壁面几何形态的近似表达,通过RNG-湍流模型和离散相模型(discrete phase model, DPM),对水轮机活动导叶端面间隙挟沙水流进行了非定常数值计算,得到了不同磨蚀阶段主要磨蚀面的平均磨损率分布,建立了过流壁面磨蚀深度变化量关于平均磨损率和磨蚀时间的数学模型和近似求解方法,预测了过流壁面的渐变磨蚀形态,分析了导叶端面和台阶面磨蚀形态逆流向演变的流动机理。数值预测结果与机组实际运行时间对应磨蚀面的磨蚀深度基本一致,平均误差在10.2%以内,验证了该预测方法的有效性。该研究可为流体机械的磨蚀预测提供参考。
计算机仿真;模型;磨蚀;水轮机活动导叶;端面间隙流;时空演变
0 引 言
水轮机内挟沙水流对活动导叶端面间隙会造成严重的磨蚀破坏,使得活动导叶间隙增大,漏水量增加,造成水轮机效率下降,机组出力减少以及水轮机在停机活动导叶关闭后转速过高而无法投入制动,水轮机检修周期缩短,电站经济损失巨大等危害[1-4]。针对上述危害,诸多研究者分析并提出了相应的解决措施[5-6]。
随着多相内流理论和数值模拟技术的发展,CFD技术已经成为研究水力机械过流部件含沙水磨损的重要手段[7-8]。近年来,国内外研究人员对水轮机机组间隙流动和磨蚀问题从试验和数值[9]计算两方面进行了研究。肖微等[10-12]研究了水轮机间隙内的流动特性。胡全友等[13-14]基于Mixtrue模型对混流式水轮机内泥沙磨损进行数值模拟。李远余[15]采用CFX软件模拟了水轮机内部含沙水流动。张广等[16-17]研究了泥沙介质在水轮机转轮中的分布规律以及对转轮压力场的影响。廖伟丽等[18]采用N-S方程和标准紊流模型比较了活动导叶有无间隙2种情况下的水轮机活动导叶水动力学特性。谭伦慧等[19]基于Reynolds平均法的Realizable模型对大流量工况、最优工况下不同高度端面间隙进行内部流场分析。Koirala等[20]在挟沙水条件下,通过对涡轮机的活动导叶叶片各主要面的侵蚀问题进行了研究,进而得出引起间隙处的横流,后缘处的尖端泄漏和表面上的高摩擦的原因。Thapa等[21]研究了5种不同尺寸间隙的情况,得出了泄漏速度及其影响最大的临界间隙尺寸的存在。国内外对磨蚀问题研究较多,但是对磨蚀演变过程的分析研究较少。
本文将水轮机活动导叶端面间隙流简化为圆柱绕流(活动导叶转轴)和台阶流动。在其磨蚀问题方面,邓丽颖[22]采用大涡模拟,对后台阶流的瞬时流场进行数值模拟,研究得到再附点的位置、平均速度场及均方根速度场。闰洁等[23]采用Lagrangian方法追踪了颗粒在圆柱近壁区的运动,利用非弹性碰撞模型的壁面磨蚀量经验公式,研究分析不同粒径的颗粒与壁面的碰撞磨蚀情况。姚军[24]分析圆柱绕流颗粒粒径对颗粒扩散分布的影响。魏治强等[25]采用Mixture多相流模型,数值计算得出泥沙颗粒在圆柱前端及后台阶区域内较为集中。邱晓等[26]采取欧拉-拉格朗日耦合算法对后台阶分离流动中颗粒扩散运动进行数值研究。Scharnowski等[27]采用平面和立体声粒子图像测速测量,研究了后台阶流产生的涡结构。
现有的磨蚀预测大多是基于流动边界条件不变的前提下进行的,然而过流表面磨蚀后,流动边界的变化使流体动力学参数也随之发生改变,导致现有的磨蚀预测很难与实际一致。本文基于磨蚀微分求积的思想,构造了主要磨蚀壁面几何形态的近似表达。本文以水轮机活动导叶端面固液两相间隙流为研究对象,基于离散相模型(discrete phase model, DPM),通过非定常数值模拟,得到主要磨蚀壁面的平均磨损率,再根据磨蚀微分求积法得到不同阶段的过流壁面的磨蚀形态,分析一个磨蚀周期内过流壁面的磨蚀形态的时空演变过程,为流体机械磨蚀破坏的有效预测提供参考。
1 计算模型
1.1 基本假设
以挟沙水流为介质,水轮机活动导叶端面间隙流动可以简化为圆柱绕流和后台阶流动,假设如下:1)固液两相挟沙水流不可压缩,沙粒为粒径均匀的球体;2)间隙流动进口固液两相没有速度滑移,并且入流方向一致。
1.2 几何模型及网格划分
1.2.1 磨蚀初期数值计算几何模型
水轮机活动导叶端面间隙流动区域简化几何模型如图1所示,该间隙是指在活动导叶瓣体端面与顶盖、底环过流面间的间隙。其中圆柱绕流为流体绕活动导叶转轴流动,上下台阶为活动导叶和顶盖台阶面。水轮机实际运行过程中,活动导叶头部端面、转轴迎流面及转轴中线之前的其他区域磨蚀破坏较轻,因此本文主要侧重于转轴背面、台阶面和活动导叶尾缘端面磨蚀形态演变过程的研究。
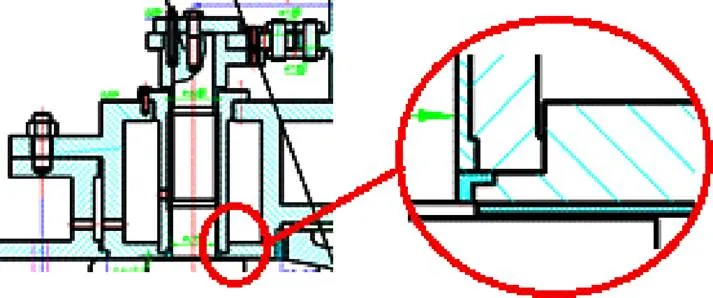
图1 水轮机活动导叶间隙流动区域简化几何模型
图2为水轮机活动导叶端面间隙流域初始简化模型正/俯视图。模型的主要几何参数及尺寸见表1。
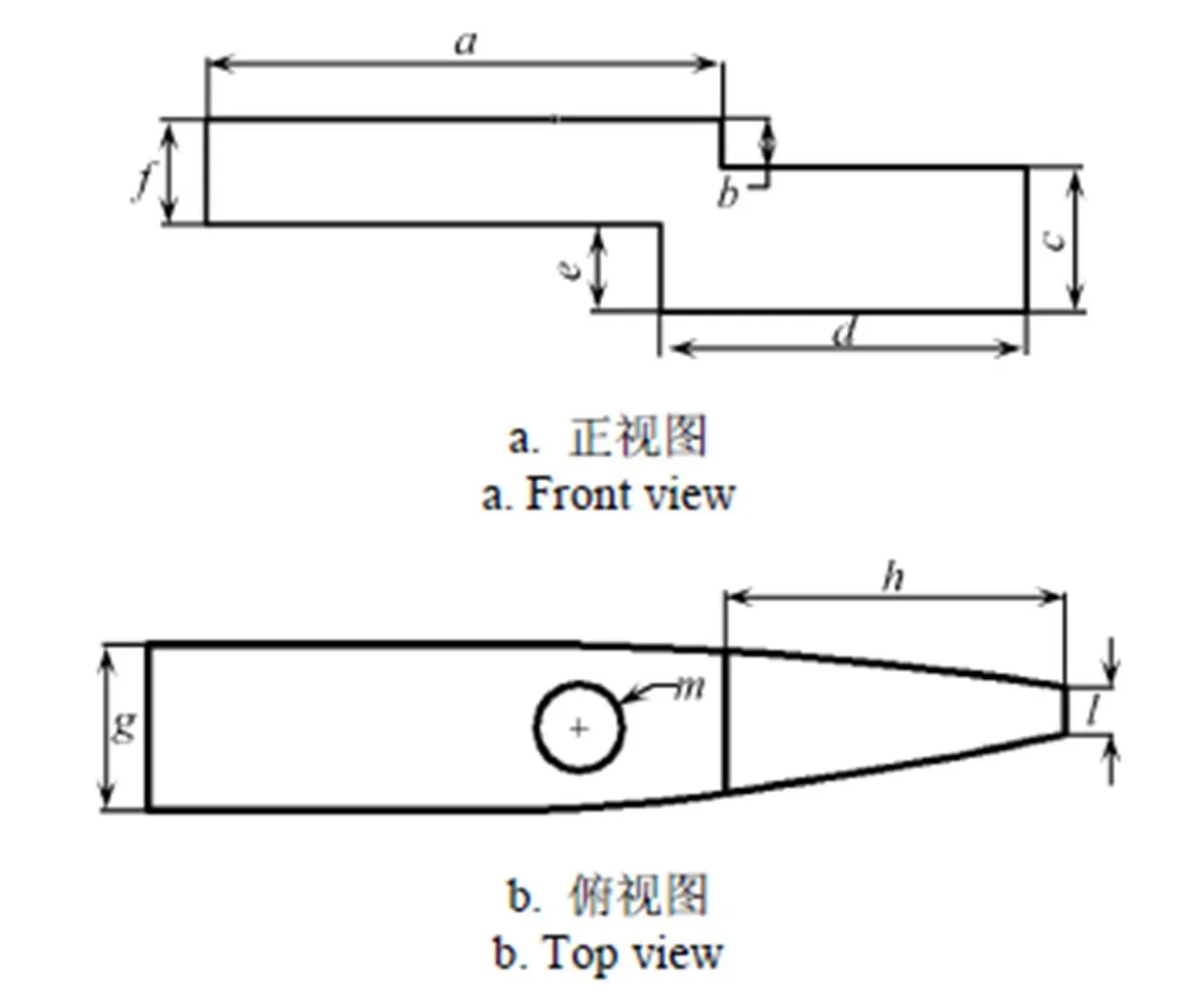
注: 模型的主要几何参数及尺寸见表1。
1.2.2 流动区域网格划分
活动导叶端面间隙流几何模型采用结构化六面体网格划分,由于磨蚀到一定程度之后,微元面Part上的磨蚀深度变化很不规律,所以间隙流磨蚀模型后几个阶段采用非结构网格进行划分。初始时刻,间隙流磨蚀模型磨损初期网格划分如图3所示。为了减少网格数量对计算结果的影响,选择不同的网格尺度,以出口压力变化量小于5%为网格无关性检验标准,进行了网格无关性检验,得出当网格数量大于60万后,间隙流模型的出口压力变化在5%以内。最终确定计算周期0、0.2、0.4、0.6、0.8和时刻间隙流几何模型的网格单元总数分别为642 784,899 358,1 404 345,652 793和624 595个。图3为间隙流模型磨蚀初始的计算域网格。

表1 模型A的主要几何参数
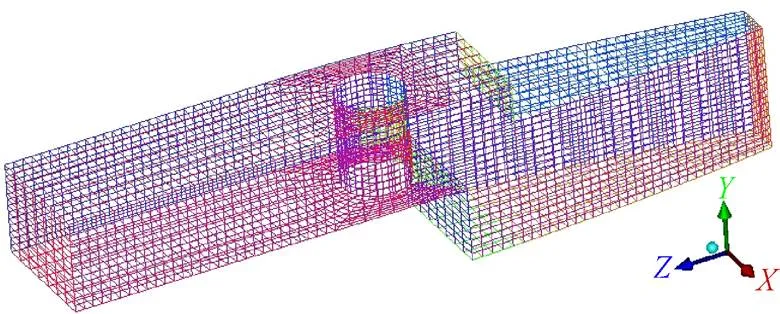
图3 初始时刻几何模型网格划分
1.3 数值计算方法
采用RNG-湍流模型和离散相模型来计算间隙流(含圆柱绕流和台阶流)的非定常三维流场,使用有限体积法和半隐式SIMPLE算法对流动控制方程进行离散和求解。非定常计算时间步长为0.000 1 s,间隙流特征时间为0.922 s,故设置每10 000步为一个计算周期Δ(1 s)。
离散相模型将固体颗粒相视为离散介质,通过积分拉氏坐标系下的颗粒运动方程来求解离散相颗粒的轨道[28-30]。颗粒运动方程在笛卡尔坐标系下的形式为

式中v为颗粒速度,m/s;为流体速度,m/s;ρ为颗粒密度,为流体密度,kg/m3;F为单位质量颗粒所受到的阻力,N;为固体颗粒所受的其他外力的总合力。
1.4 边界条件和初始条件
根据三元水电公司对该型水轮机的测试和全流场数值计算结果,水轮机活动导叶端面间隙流入口边界采用速度进口,进口速度为10 m/s,入口面压力Patch为1.9 MPa;出口边界采用自由出流。清水相密度为998.2 kg/m3,黏度为0.001 003 kg/(m·s);考虑重力的影响,重力加速度取9.81 m/s2;沙粒平均密度取2 650 kg/m3,中值粒径取0.05 mm,颗粒体积相含率取7%。活动导叶端面材料为ZGO4Cr13Ni5Mo,材料密度为7 790 kg/m3。入口处设置为固相入射面源,且颗粒均匀分布。壁面边界采用无滑移边界条件,间隙流壁面采用反射边界,颗粒在此壁面处反弹并发生动量变化,出口采用逃逸边界。
1.5 壁面磨蚀计算模型
实践表明,挟沙水流对水轮机活动导叶端面间隙表面以及活动导叶轴的磨蚀是一个非均态的逆流向发展过程。为了比较准确的描述该间隙磨蚀发展演变的物理真实,本文采用磨蚀微分求积法,在需要考虑的磨蚀面上创建尽可能多的微元面,构造其表面形态的渐近几何表达,然后根据数值计算结果所求得各微元面Part上的平均磨损深度微量Δδ来改变间隙流模型磨蚀后的表面形态,通过微分求积的思想得出这一问题的数值近似解。

式中为一个磨蚀计算周期;()为某一时刻的磨蚀深度,mm;为某一磨蚀时刻;为第个磨蚀时段;δ为某一时段的磨蚀深度,mm。由非定常数值模拟一个计算周期Δ内的计算结果,得到每个微元面Part的平均磨损率I。平均磨损率定义为[31-32]

式中I单位面积上壁面的磨损速率,kg/(m2·s);为单元面积上碰撞的颗粒数目;m为碰撞颗粒的质量流率,kg/s;(d)为与颗粒粒径相关的函数;d为颗粒中值直径,mm;为颗粒对壁面的冲击角;()为此相对速度的函数,取1;为颗粒相对于壁面的速度,m/s;face为壁面计算单元面积,m2。
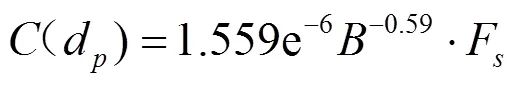
式中F为颗粒形状因子,颗粒为球形取0.2;为布氏硬度。冲击角函数可通过分段性函数拟合得到。
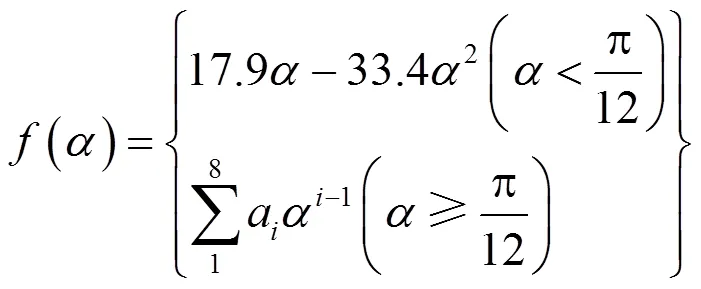
式中()冲击角函数;为冲击角;a为常数。
利用平均磨损率与磨蚀深度的关系,得到时间段间隙表面几何形态的磨蚀深度变化量Δδ,直到间隙表面几何形态与实际运行中磨蚀程度近似一致截止。令Δδ为局部磨蚀深度,则壁面磨蚀深度的渐变模型为
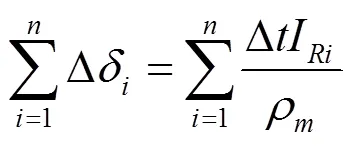
式中I为微元面对应的平均磨损率,kg/(m2·s);Δ为磨蚀时间,s;ρ为过流壁面的材料密度,kg/m3;δ为微元面对应的磨蚀深度,m。
2 磨蚀计算结果与分析
2.1 顶盖台阶面和端面平均磨蚀率变化及分析
图4为一个磨蚀周期内不同时段顶盖台阶面和端面平均磨蚀率分布图。由图4可知,在初始阶段,绕流活动导叶转轴的流体,由于过流段面面积急剧减少,在台阶面中心为卡门涡,两侧为高速下冲流体。台阶面两侧表现为冲击磨蚀,中间为卡门涡磨蚀,故顶盖台阶面两侧和中间平均磨蚀率均较大,形成“w”型初始磨蚀坑。随着磨蚀坑的形成,卡门涡对顶盖台阶面磨蚀的影响相对变小,使得顶盖两侧冲击磨蚀成为磨蚀的主要因素。
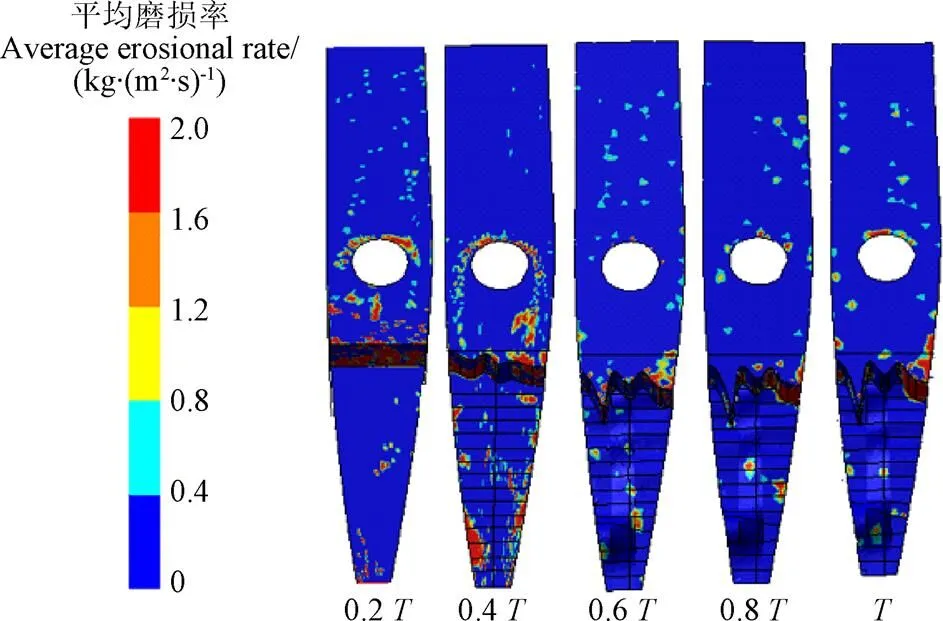
注:T为一个磨蚀周期。
顶盖端面在初始阶段,由于回流涡的产生,颗粒较少的碰撞和摩擦过流壁面,因此平均磨蚀率较小。顶盖端面下游由于活动导叶翼型产生渐缩流道及上冲流,使得平均磨蚀率增大,在磨蚀0.6后,由于活动导叶端面形成较大磨蚀坑,上冲流的影响减小,使得顶盖端面下游的平均磨蚀率又重现减小的趋势。
2.2 活动导叶台阶面和端面平均磨蚀率变化及分析
图5为不同时空域下活动导叶台阶面和端面平均磨蚀率分布图。从图中5可以看出,活动导叶台阶面由于非对称翼型的原因,使得台阶回流涡在活动导叶台阶面一侧发展较充分,圆盘切割效应使一侧平均磨蚀率较大,并逐渐形成蜂窝状磨蚀坑,随着磨蚀坑发展,颗粒圆盘切割效应逆流向台阶内发展。
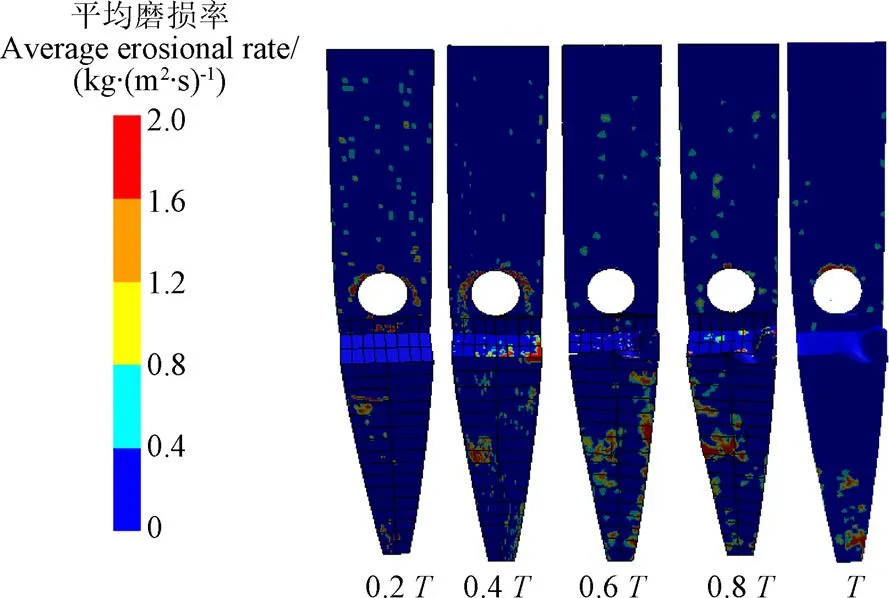
图5 不同时空域下活动导叶台阶面和端面平均磨蚀率
活动导叶端面由于台阶涡后下冲流的冲击磨蚀,在活动导叶端面流体再附点附近形成最大磨蚀率,从而形成初始的磨蚀带。随着带状磨蚀坑的发展和再附点后移,使得活动导叶端面的最大磨蚀率的位置逐渐后移。
2.3 活动导叶转轴背面平均磨蚀率变化及分析
图6为不同时空域下转轴背面磨蚀率分布图。由于圆柱绕流,转轴背面出现较对称排列的卡门涡街,圆盘切割效应造成转轴背面出现了几乎对称的2个磨蚀坑。在0.4时刻,转轴背面对称位置上的磨蚀率出现最大值。在转轴背面几何形态磨蚀到一定程度后,其磨蚀率逐渐趋于稳定。
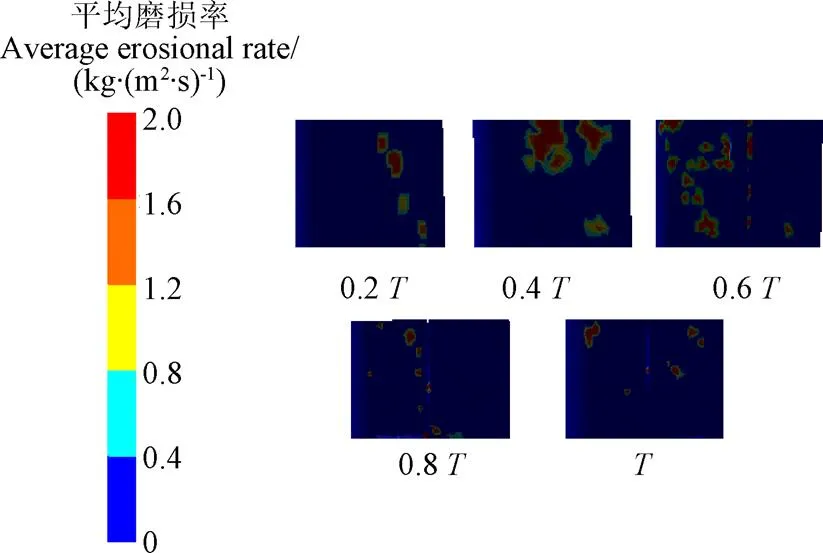
图6 不同时空域转轴背面平均磨蚀率
2.4 活动导叶端面间隙磨蚀形态变化预测
图7为0~时刻水轮机活动导叶端面间隙表面几何形态变化过程。在0.2时刻顶盖台阶面、顶盖端面和活动导叶端面由于磨蚀表面已经开始出现不规则的磨蚀坑。在0.2~0.4时刻,活动导叶端面间隙主要过流壁面的形态变化最为剧烈。由于非对称渐缩翼型的影响,在0.4、0.6、0.8和磨蚀坑深度比较高的区域都在间隙流右侧(从进口方向看),如顶盖台阶面右侧和活动导叶台阶面右侧。从0.2到时刻,回流涡的产生,使得涡的外缘处沙粒不断侵蚀活动导叶台阶面,磨蚀深度加深,再附点区域的磨蚀深度和面积也在逐渐加大并随着回流涡向上游移动而移动。
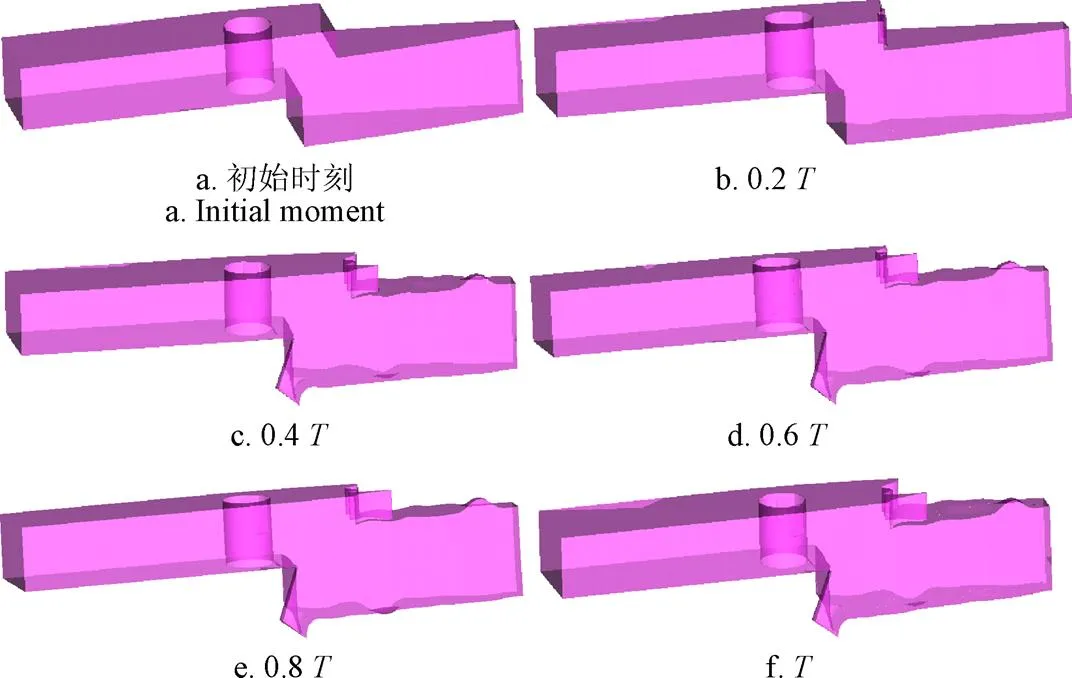
图7 不同时刻下间隙流表面形态
3 活动导叶端面间隙磨蚀形态的验证与分析
根据甘肃酒泉三元水电开发有限公司水轮机活动导叶间隙磨蚀的数据,以过流壁面预测磨蚀形态与实际磨蚀形态基本一致为一个磨蚀周期,将一个磨蚀形态变化周期分为5个时间阶段(如表2所示),每个磨蚀阶段机组实际运行1 361 h,对应数值计算磨蚀时间为4.9×106s;整个磨蚀周期机组运行6 805 h,对应数值计算磨蚀时间24.5×106s。
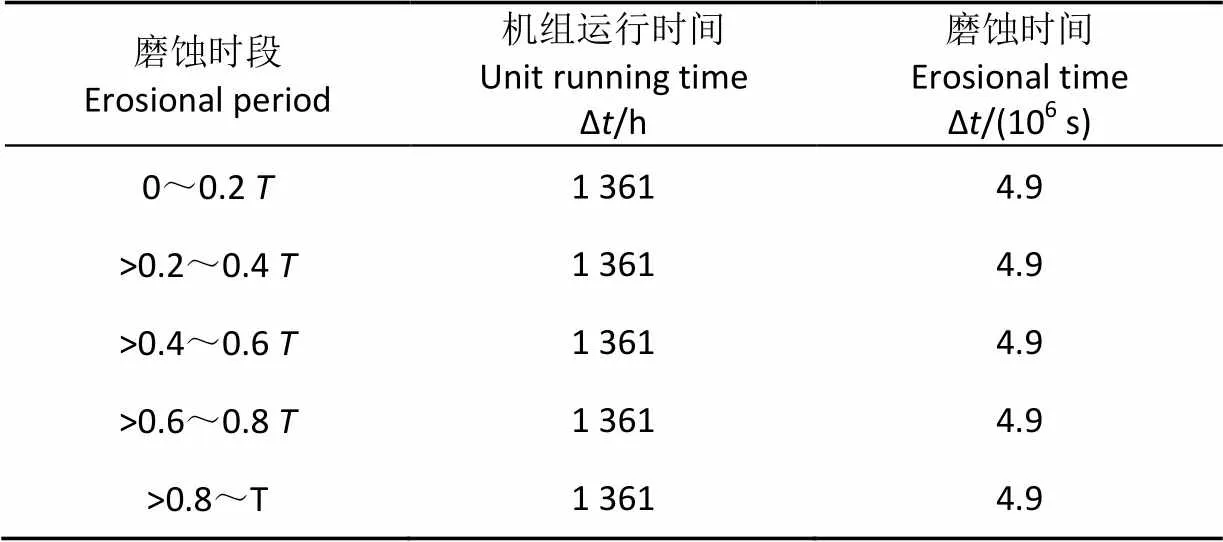
表2 机组运行时间与磨蚀量预测时间对比
将水轮机活动导叶机组实际运行6 805 h后,活动导叶端面间隙流的磨蚀情况与数值模拟结果进行磨蚀位置和深度的对比分析。图8为顶盖下表面磨蚀位置的数值模拟结果与实际磨蚀情况的对比图。由图8可知,数值模拟所得到的顶盖下表面的磨蚀位置为顶盖台阶面以及顶盖端面,顶盖端面出现带状和块状磨蚀区域,顶盖台阶面出现块状磨蚀带,与实际磨蚀位置一致,这些位置的平均磨蚀率主要分布在1.6~2.0 kg/(m2·s)。

图8 顶盖下表面磨蚀位置的数值模拟结果与实际对比图
图9为顶盖下表面磨蚀监测点的设置示意图。其中图9a、图9b分别表示时刻活动导叶间隙流模型顶盖下表面的实际磨蚀几何形态,在顶盖端面设置8个监测点,顶盖台阶面设置13个监测点,图9c为实际磨蚀情况图片。顶盖端面的8个点分别等距布置在顶盖端面磨蚀较重的区域,顶盖台阶面的13个监测点等距布置在活动导叶台阶面处磨蚀较深的区域,计算模型上的监测点按比例与实际布置点相同。由数值模拟结果图9a可知在2,3,4,5,6监测点上磨蚀较深,图9b在3,4,5,9,13监测点上磨蚀较深。与实际磨蚀情况图9c进行比较,结果基本一致。
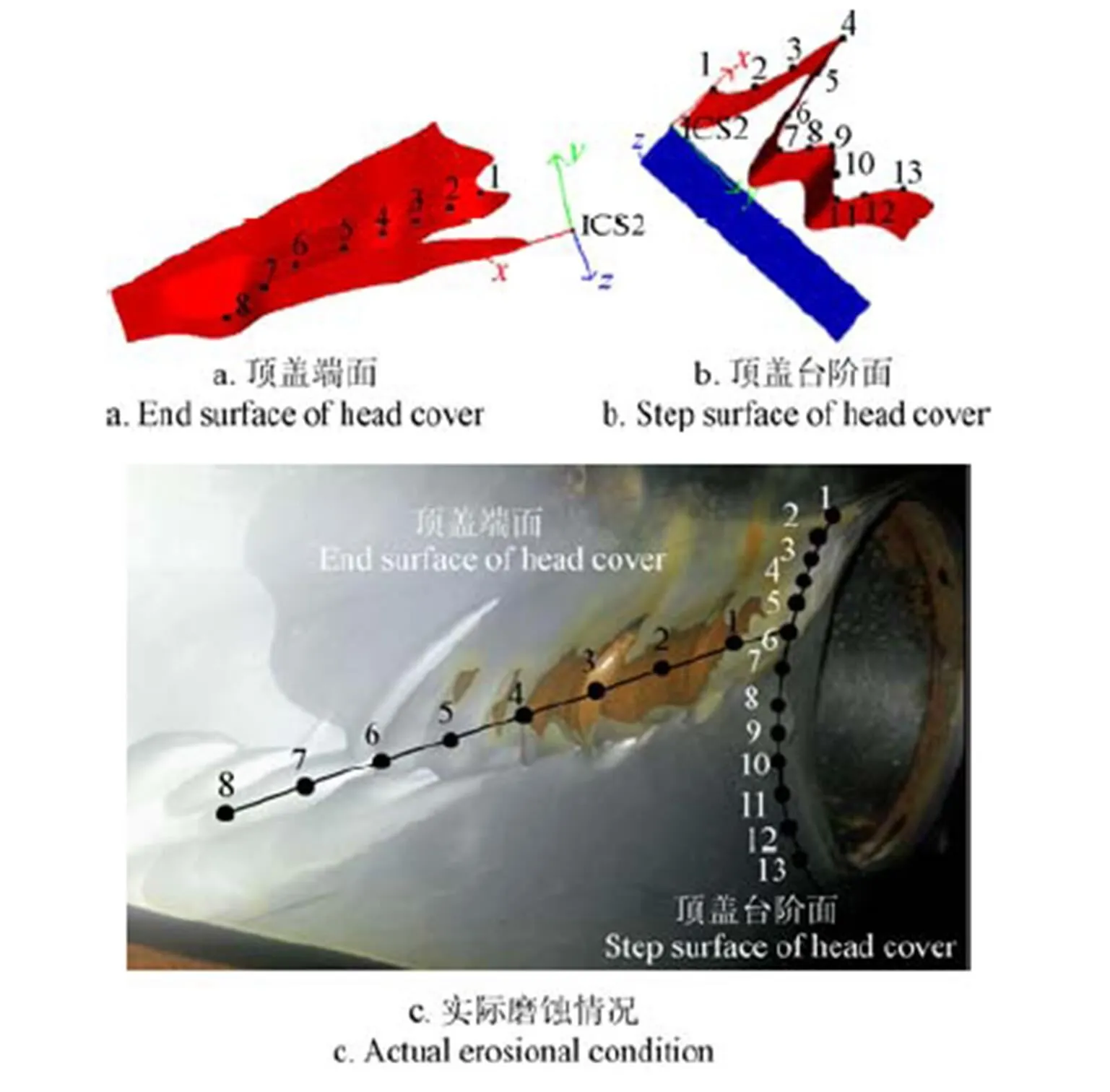
图9 顶盖下表面磨蚀监测点
图10为顶盖下表面所设监测点深度与实际磨蚀相应位置磨蚀深度对比。由图10可知,计算结果和实际磨蚀深度大致吻合,顶盖台阶面磨蚀深度平均误差为6%;顶盖端面磨蚀深度平均误差为7.8%,说明简化流动模型和磨蚀预测计算模型可较准确的预测活动导叶端面间隙流的磨蚀情况。
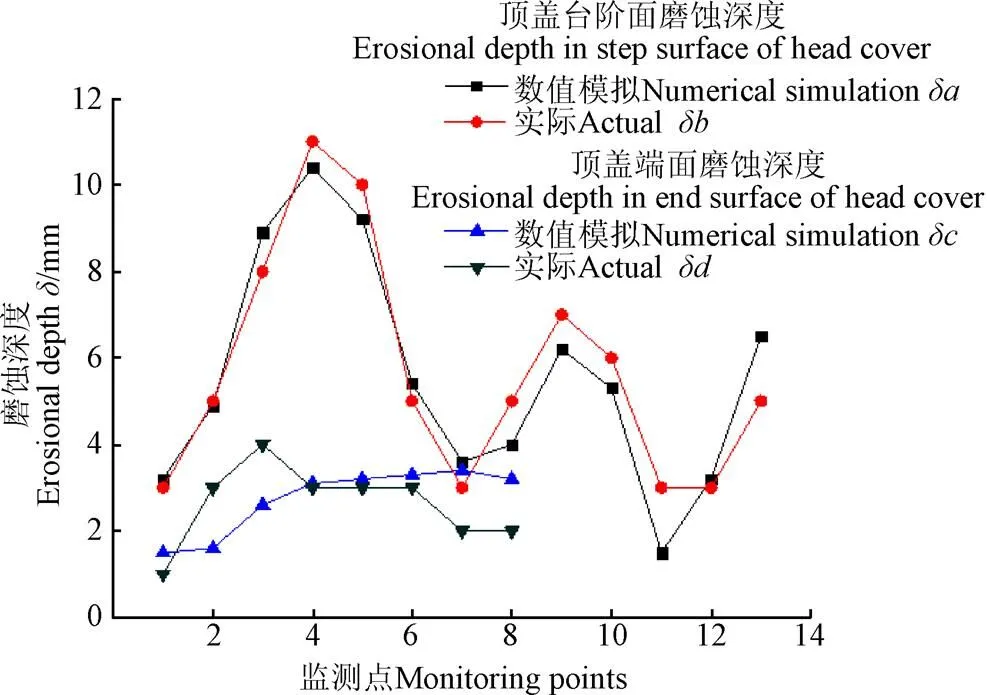
图10 顶盖下表面监测点磨蚀深度
图11为活动导叶上表面磨蚀数值模拟结果与实际磨蚀情况对比图。由图11可以看出,数值模拟得到的活动导叶上表面的磨蚀位置与实际磨蚀位置一致,主要为活动导叶转轴背面、活动导叶台阶面以及活动导叶端面。磨蚀具体区域和形状与实际图片吻合,即活动导叶转轴背面的磨蚀主要集中在紧靠顶盖下表面的区域,磨蚀形状为2个几乎对称的块状磨蚀坑;活动导叶台阶面的磨蚀集中在以进口为正方向的左侧的块状磨蚀坑;活动导叶端面的磨蚀形状为带状磨蚀坑。
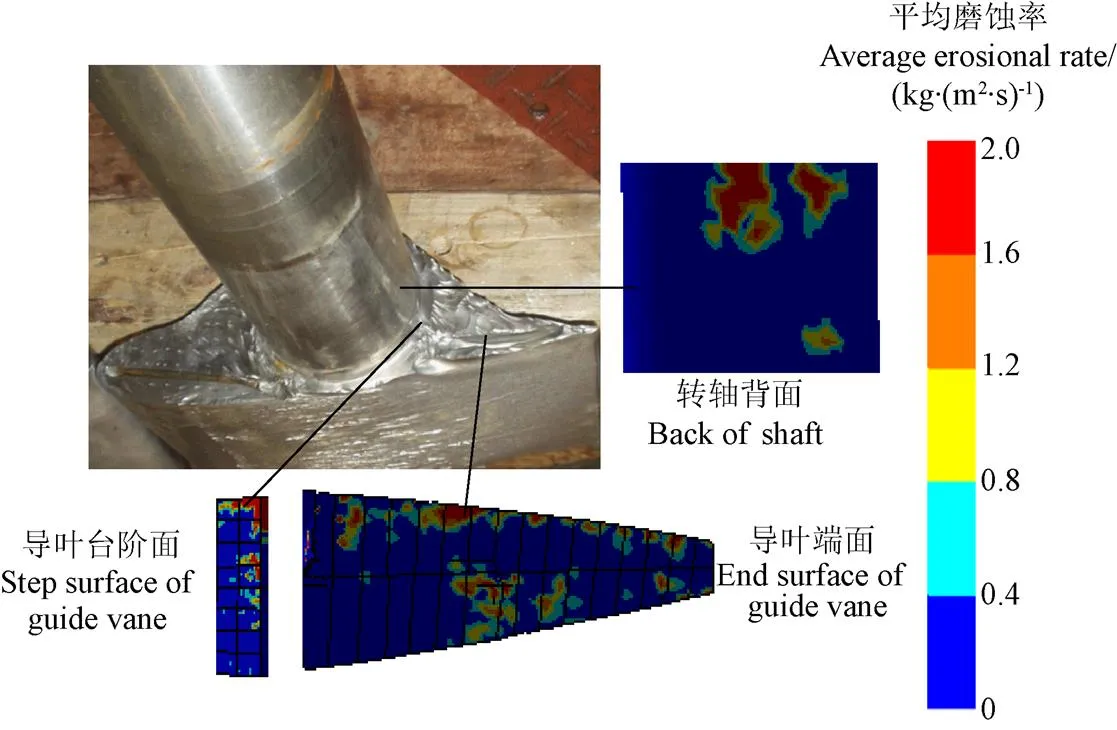
图11 活动导叶上表面磨蚀的数值模拟结果与实际对比图
图12为活动导叶上表面磨蚀监测点的设置示意图。图12a、图12b分别表示时刻活动导叶间隙流模型活动导叶上表面的磨蚀几何形态,在活动导叶端面和活动导叶台阶面分别设置8个监测点,图12c为实际磨蚀情况图片。顶盖端面的8个点分别等距布置在活动导叶端面磨蚀较重的区域,顶盖台阶面的8个监测点等距布置在活动导叶台阶面处磨蚀较深的区域,计算模型上的监测点按比例与实际布置点相同。由数值模拟结果图a可知在1,2,3监测点上磨蚀较深,图b在1,2,4监测点上磨蚀较深。与实际磨蚀情况图c进行比较,结果基本一致。

图12 活动导叶上表面磨蚀监测点
图13为活动导叶台阶面和端面所设监测点磨蚀深度与实际相应位置磨蚀深度对比。由图可以看出,计算结果和实际磨蚀深度大致吻合,活动导叶台阶面磨蚀深度平均误差为8%;活动导叶端面磨蚀深度平均误差为10.2%,说明简化流动模型和磨蚀预测计算模型可以比较准确的预测活动导叶端面间隙流的磨蚀问题。

图13 活动导叶台阶面和端面监测点磨蚀深度
4 结 论
本文在离散相模型的框架内,建立了水轮机活动导叶间隙泥沙流动数值计算模型,分析了挟沙水在活动导叶间隙内部速度以及磨蚀分布情况,主要结论如下:
1)活动导叶转轴背面尾迹中出现交错排列的完全卡门涡街,转轴背面出现对称的磨蚀坑。
2)高速度的流体冲击顶盖台阶面造成磨蚀,下台阶下游再附点向下游移动;活动导叶上表面的回流区磨蚀少,颗粒集中在涡的外缘,此处磨蚀增加;随着活动导叶台阶处回流涡外缘处颗粒不断地侵蚀壁面,此处出现较深磨蚀坑,回流涡向上游移动,活动导叶端面再附点也随着逆流动方向向上游迁移,导致活动导叶端面的磨蚀坑出现逆流动的向上游壁面区域的磨蚀面积明显增加;由于活动导叶翼型为不对称渐缩翼型,磨蚀在右侧(从入口方向看)的磨蚀较严重。
3)从0.2到0.4(为一个磨蚀周期)时刻,水轮机活动导叶磨蚀形态变化最剧烈。
4)数值模拟结果与实际磨蚀测量数据表明磨蚀位置和深度基本一致,平均误差在10.2%以内,说明模型简化的合理性,计算模型选择和数值模拟结果是有效的。本文可对流体机械过流部件表面磨蚀预测方法提供参考。
致谢:感谢甘肃省酒泉市三元水电开发有限公司为本文提供水轮机活动导叶端面、转轴以及顶盖端面的磨蚀测量数据。
[1] 赵当. 水轮机导水机构漏水影响原因分析及处理[J]. 科技风,2013(23):13.
Zhao Dang. The analysis and treatment of water leakage in hydraulic turbine water diversion mechanism[J]. Science and Technology, 2013(23): 13. (in Chinese with English abstract)
[2] 顾四行,贾瑞旗,张弋扬,等. 水轮机磨蚀与防治[J]. 水利水电工程设计,2011(1):39-43.
Gu Sixing, Jia Ruiqi, Zhang Yiyang, et al. Erotion and prevention of hydraulic turbine[J]. Design of Water Resources and Hydropower Engineering, 2011(1): 39-43. (in Chinese with English abstract)
[3] 王韧. 水轮机磨蚀与防治措施[J]. 科技创新与应用,2017(2):157.
Wang Ren. Turbine erosional and control measures[J]. Science and Technology Innovation and Application, 2017(2): 157. (in Chinese with English abstract)
[4] 许迎萍. 水电站水轮机磨损与防护[J]. 科技风,2014(5):9.
Xu Yingping. Erosional and protection of hydropower station[J]. Science and Technology, 2014(5): 9. (in Chinese with English abstract)
[5] Koirala R, Zhu B, Neopane H P. Effect of guide vane clearance gap on francis turbine performance[J]. Energies, 2016, 9(4): 275.
[6] 王轩,白刚. 锦屏一级水电站水轮机导叶端面间隙调整及影响因素分析[J]. 中国水能及电气化,2015(12):37-41.
Wang Xuan, Bai Gang. Analysis on turbine guide vane end clearance adjustment and influence factors in Jinping first cascade hydropower station[J]. Water and Electrification of China, 2015(12): 37-41. (in Chinese with English abstract)
[7] 高忠信,陆力. CFD技术在水力机械研究中的应用[J]. 中国水利,2008(21):76-78,82. Gao Zhongxin, Lu Li. Application of CFD technology in Hydro-machinery studies[J]. China Water Resources, 2008(21): 76-78,82. (in Chinese with English abstract)
[8] 乔文涛. 基于CFD的混流式水轮机内流场计算与分析[D]. 郑州:华北水利水电大学,2016.
Qiao Wentao. Financial Field Calculation and Analysis of Francis Turbine based on CFD[D]. Zhengzhou: North China Institute of Water Conservancy and Hydropower, 2016. (in Chinese with English abstract)
[9] 易艳林,陆力. 水轮机泥沙磨损研究进展[J]. 水利水电技术,2014,45(4):160-163.
Yi Yanlin, Lu Li. Progress of research on silt abrasive erosion of hydraulic turbine[J]. China Academy of Water Resources and Hydropower, 2014, 45(4): 160-163. (in Chinese with English abstract)
[10] 肖微. 轴流转桨式水轮机含间隙的内部流动数值研究与分析[D]. 西安:西安理工大学,2007.
Xiao Wei. Numerical Study and Analysis of Inner Flow Field Including the Flange Clearance Region of Kaplan Turbine[D]. Xi’an: Xi’an University of Technology, 2007. (in Chinese with English abstract)
[11] 王文全,尹锐,闫妍. 不同雷诺数下混流式水轮机密封间隙通道内流动特征分析[J]. 排灌机械工程学报,2014,32(7):611-616.
Wang Wenquan, Yin Rui, Yan Yan. Analysis of flow in side chamber and path of comb-labyrinth seal in francis turbine at different Reynolds numbers[J]. Journal of Drainage and Irrigation Machinery Engin, 2014, 32(7): 611-616. (in Chinese with English abstract)
[12] 冯建军,罗兴锜,吴广宽,等. 间隙流动对混流式水轮机效率预测的影响[J]. 农业工程学报,2015,31(5):53-58. Feng Jianjun, Luo Xingqi, Wu Guangkuan, et al. Influence of clearance flow on efficiency prediction of francis turbines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(5): 53-58. (in Chinese with English abstract)
[13] 胡全友,刘小兵,赵琴. 基于两相流动理论的混流式水轮机叶轮内泥沙磨损的数值模拟[J]. 水电能源科学,2016,34(7):183-186.
Hu Quanyou, Liu Xiaobing, Zhao Qin. Numerical simulation of sediment wear in francis turbine impeller based on two-phase flow theory[J]. Journal of Hydroelectric Energy Science, 2016, 34(7): 183-186. (in Chinese with English abstract)
[14] 黄剑峰,张立翔,姚激,等. 水轮机泥沙磨损两相湍流场数值模拟[J]. 排灌机械工程学报,2016,34(2):145-150.
Huang Jianfeng, Zhang Lixiang, Yao Ji, et al. Numerical simulation of two-phase turbulent flow in turbine sediment Wear[J]. Journal of Hydraulic Engineering and Engineering, 2016, 34(2): 145-150. (in Chinese with English abstract)
[15] 李远余. 高比速混流式水轮机固液两相数值模拟[D]. 哈尔滨:哈尔滨工业大学,2014.
Li Yuanyu. High-speed Mixed-Flow Turbines Solid-Liquid Two-Phase Numerical Simulation[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese with English abstract)
[16] 张广,魏显著. 泥沙浓度及粒径对水轮机转轮内部流动影响的数值分析[J]. 农业工程学报,2014,30(23):94-100.
Zhang Guang, Wei Xianzhu. Numerical analysis for effects of concentration and diameter of sediment on solid-liquid two-phase flow in hydraulic turbine runner[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(23): 94-100. (in Chinese with English abstract)
[17] 张广,魏显著,宋德强. 活动导叶端面间隙泥沙磨蚀数值预测研究[J]. 大电机技术,2017(3):64-68.
Zhang Guang, Wei Xianzhu, Song Deqiang. Study on numerical prediction of sediment wear in end face of guide vane[J]. Large Electric Machine Technology, 2017(3): 64-68. (in Chinese with English abstract)
[18] 廖伟丽,李建中. 水轮机活动导叶含端面间隙的水动力学研究[J]. 水利学报,2003(2):43-47,54.
Liao Weili, Li Jianzhong. Study on hydrodynamics of turbine guide vanes with end face clearances[J]. Chinese Journal of Water Resources, 2003(2): 43-47, 54. (in Chinese with English abstract)
[19] 谭伦慧,李彦瑞. 径向式导水机构活动导叶端面间隙流场数值模拟分析[J]. 能源视界,2015(12):253-254.
Tan Lunhui, Li Yanrui. Numerical simulation for hydro- turbine guide vanes including end clearance[J]. Science& Technology Vision, 2015(12): 253-254. (in Chinese with English abstract)
[20] Koirala Ravi, Thapa Bhola. A review on flow and sediment erosion in guide vanes of Francis turbines[J]. Renewable & Sustainable Energy Reviews, 2017, 75: 1054-1065.
[21] Thapa Biraj Singh, Dahlhaug Ole Gunnar. Sediment erosion induced leakage flow from guide vane clearance gap in a low specific speed Francis turbine[J]. Renewable Energy, 2017, 107: 253-261.
[22] 邓丽颖. 复杂流动下泥沙起动机理的研究[D]. 长沙:湖南大学,2009.
Deng Liying. The Sediment’s Incipience Mechanism under Complex Flow[D]. Changsha: Hunan University, 2009. (in Chinese with English abstract)
[23] 闰洁,李文春,樊建人,等. 绕流中颗粒与柱体碰撞和磨蚀的直接数值模拟[J]. 浙江大学学报,2007,41(4):589-593.
Yan Jie, Li Wenchun, Fan Jianren, et al. Direct numerical simulation of collisions and erosions between particles and cylinder in circular cylinder wake[J]. Journal of Zhejiang University, 2007, 41(4): 589-593. (in Chinese with English abstract)
[24] 姚军. 气固两相圆柱绕流的直接数值模拟研究和肋条弯管抗磨机理的数值试验研究[D]. 杭州:浙江大学,2002.
Yao Jun. Direct Numerical Simulation of Particle Dispersion in the Temporal Wake of a Circular Cylinder& Numerical Investigation of a New Method for Protecting Bends from Erosion in Gas-Particle Flows[D]. Hangzhou: Zhejiang University, 2002. (in Chinese with English abstract)
[25] 魏治强,郝晓青. 浅析基于Mixture模型的固液两相流[C]// 第十三届沈阳科学学术年会论文集,2016:743-747
Wei Zhiqiang, He Xiaoqing. Analysis of solid - liquid two- phase flow based on mixture model[C]//The Proceedings of the 13th Shenyang Science Academic Conference, 2016: 743-747. (in Chinese with English abstract)
[26] 邱晓,丁珏,王忠杰,等. 湍流分离流中颗粒的扩散机制[J]. 上海大学学报,2016,22(5):586-596.
Qiu Xiao, Ding Jue, Wang Zhongjie, et al. Particles diffusion mechanism in turbulent separation flow[J]. Journal of Shanghai University, 2016, 22(5): 586-596. (in Chinese with English abstract)
[27] Scharnowski Sven, Bolgar Istvan. Characterization of turbulent structures in a transonic backward-facing step flow[J]. Flow Turbulence and Combustion, 2017, 98(4): 947-967.
[28] Fluent Ansys. Theory Guide[M]. US: ANSYS Inc, 2009.
[29] Ge W, Li J. Macro-scale phenomena reproduced in microscopic systems-pseudo-particle modeling of Fluidization[J]. Chemical Engineering Science, 2003, 58(8): 1565-1585.
[30] Sun Q H, Li J H. A novel pseudo-particle model for gas-solid two-phase flow[J]. Engineering Chemistry and Metallurgy, 1999, 3: 19.
[31] Quamrul H, Mazumder. Prediction of erosion due to solid particle impact in single-phase and multiphase flows[C]// ASME International Mechanical Engineering Congress and Exposition, Orlando, Florida, USA, 2005: 775-786.
[32] Mclaury B S. A Model to Predict Solid Particle Erosion in Oilfield Geometries[D]. Tulsa:University of Tulsa, 1993.
Prediction of erosional shape evolution in end-surface clearance of turbine guide vane
Han Wei1,2, Chen Yu1, Liu Yi1,2※, Wei Sanze3, Li Guangxian1, Jin Junjun1
(1.730050; 2.730050; 3.735000)
Most of the existing erosional prediction is based on the premise of constant flow boundary conditions. However, when the flow surfaces are corroded, the hydrodynamic parameters changed with the change of the flow boundary. Thus, the existing erosional prediction approach is difficult to be consistent with the reality. The practice shows that the end clearance surface and the shaft of the turbine guide vane are corroded by sand-laden water, which is a development process of non-homogeneous and backward. The generation of erosional damage has a negative impact on the normal operation of the unit and the safety of production. In order to accurately describe the physical reality of the erosional shape evolution of the end clearance surface,in this article, we proposed erosional differential quadrature concept. The approximate expression of the geometric shape in the main erosional surface was constructed by creating as much surfaces. The numerical simulation methods combined RNG(Re- normalization group) turbulence model with DPM (discrete phase model) was applied. According to the test and numerical results of the full flow field for San-yuan hydropower company, the calculated boundary conditions and initial conditions were set. The model inflow boundary could be assumed to be velocity inlet and outflow. The inlet speed was 10 m/s, and the pressure of inlet was 1.9 MPa. The model of the end clearance flow of turbine guide vane under sand-laden water was simplified as the flow around a circular cylinder and a step, and then the three-dimensional unsteady numerical calculation was carried out. The average erosional rate distributions were obtained on the main erosional surface at different stage. The main erosional surfaces include the back of shaft as well as the step surface of the guide vane and the head cover. The mathematical model and approximate solution method of average erosional rate and erosional time related to erosional depth variation on flow surface were established. The surface morphology of the clearance flow model was changed according to the amount of erosional depth variation. When the geometrical form of the clearance flow surface was approximately the same as the degree of erosion in the actual operation, the geometrical form of model was no longer changed. Thereby, the gradual erosional shape of the flow surface was predicted. The temporal and spatial evolution of the erosional morphology on the flow wall during the period of erosion was analyzed, and then the flow evolution mechanism of the backflow on the end surface and the step surface of the turbine guide vane was analyzed. As the particles at the outer edge of the vortex in the step surface of the guide vane continually to erode the surfaces, where the deep erosional pits appeared, the vortex developed backwards, the reattachment position on the guide vane surface was also migrated upstream, and then the erosional area had a significant increase and also migrated upstream. In addition, the main reason for the erosion behind the shaft was the generation of the Karman Vortex Street. Due to the airfoil of guide vane was the asymmetric reduction, the erosion on the right side (observing from the entrance direction) was more serious. When the period was from 0.2to 0.4, the change degree of erosional morphology on turbine guide vanes were the most intense. The numerical results were approximately similar to the erosional depth on the erosional surface under the actual running time of the unit, which verified the validity of the method. This paper provides a reference for effective prediction of the erosional condition of fluid machinery. In addition, it also provides a theoretical reference for structural design, erosional protection and material selection in the end clearance surface of turbine guide vane.
computer simulation; models; erosion; turbine guide vane; end-surface clearance flow; spatiotemporal evolution
2017-08-06
2018-01-04
国家自然科学基金资助项目(51669012);西华大学重点实验室开放基金项目(szjj2017-092)
韩 伟,副教授,博士,主要从事水力机械内部固液两相流动理论研究。Email:hanwei@lut.cn
刘 宜,教授级高工,主要从事水力机械流动理论及优化设计方法研究。Email:18811212509@163.com
10.11975/j.issn.1002-6819.2018.04.012
TK730
A
1002-6819(2018)-04-0100-08
韩 伟,陈 雨,刘 宜,魏三则,李光贤,金俊俊. 水轮机活动导叶端面间隙磨蚀形态演变预测[J]. 农业工程学报,2018,34(4):100-107.doi:10.11975/j.issn.1002-6819.2018.04.012 http://www.tcsae.org
Han Wei, Chen Yu, Liu Yi, Wei Sanze, Li Guangxian, Jin Junjun. Prediction of erosional shape evolution in end-surface clearance of turbine guide vane[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 100-107. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2018.04.012 http://www.tcsae.org

