新常态下货币供给对工业经济的非对称冲击
——兼论冲击路径的情景设计与分析
刘 汉,黄卫挺,贺彦飞
(1. 吉林大学数量经济研究中心、商学院,吉林 长春 130012;2. 国家发改委宏观经济研究院,北京 100038;3. 辽宁省沈阳市统计局,辽宁 沈阳 110013)
1 引言
货币政策与产出和价格之间的关系一直以来都是经济学理论和实证研究的重点和热点问题,这不仅有助于理解货币政策的作用方式和传导机制等经济理论问题,还对宏观调控,尤其是货币政策调控的方向、力度和节奏具有重要的实际参考价值[1]。然而,实证研究随着研究的对象、所处的经济阶段和研究方法的不同,结论表现出很大的差异。传统研究方法是通过建立VAR模型系统来分析各变量对货币供给冲击的脉冲响应[2-7]。但是,人们在研究中发现货币政策在经济衰退阶段对经济行为的作用效果要比其在扩张阶段的作用效果更强[3],实际产出对反向货币冲击的响应要比对正向货币冲击的响应更为灵敏[8-9],这些脉冲响应的研究说明货币供给冲击对产出和价格的影响具有非线性和非对称性。事实上,Sims[10]在提出VAR模型计算脉冲响应时暗含一些假设,如:① 对称性,即正向和负向冲击的响应是互为镜像;② 冲击形态的不变性,即不同大小的冲击成比例;③ 历史独立性,即冲击的形态是独立于局部历史条件;④ 多维性,即脉冲响应是参数估计值的高维非线性函数[11]。显然,上述VAR模型隐含的假设条件并不符合现实经济情况,而且在多变量的VAR建模中,VAR模型容易出现模型误设和难以计算的问题。
针对VAR模型在计算脉冲响应函数时的缺陷,Koop等[12]和Potter[13]定义了广义脉冲响应函数,释放VAR模型在估计脉冲响应函数过程中的线性假设,随后出现了大量使用非线性计量方法来估计模型并计算其广义脉冲响应及其影响的研究,如Weise[14]运用平滑迁移门限向量自回归模型 (LSTVAR);Assenmacher-Wesche[15]使用马尔可夫机制转移模型;Lütkepohl等[16],Christopoulos和Leon-Ledesma[17]采用LSTR (logistic STR) 模型。国内也存在大量的类似研究,如冯春平[18]使用滚动VAR方法;赵进文和闵捷[19],以及赵进文和黄彦[20]使用LSTR模型;刘金全和郑挺国[21]运用马尔可夫转移模型,彭方平和王少平[22]应用非线性光滑转换面板数据模型,郑挺国和刘金全[23]使用平滑迁移向量误差修正(STVECM)模型;刘金全等[24]利用平滑迁移向量自回归 (LSTVAR) 模型等等。这些非线性模型的出现,大大丰富了货币政策作用机制的研究和发展,但是以上研究均没有脱离VAR模型的范畴,无论是线性还是非线性模型,其基本前提条件是VAR模型能够匹配其数据生成过程,若设定的VAR模型无法准确描述数据生成过程,其所计算出的脉冲响应和相应的结论将会遭到质疑,而Jorda[11],刘汉和刘金全[25]采用的投影方法对模型设定所出现的误差并不敏感,其条件置信水平也能够解决脉冲响应的序列相关问题,此外该方法还能够很便捷地对脉冲响应的冲击路径进行约束,从而在情景设计下进行政策作用效果的模拟和分析,目前已经被广泛应用于各个领域。
实证研究中很少有将工业产出和价格分离出来,研究其对货币供给冲击的影响。仅在数据量要求较大 (如多区制的MS-VAR),或需要在月度频率上进行分析时,才会采用工业增加值来代表产出[26-27]。但是,工业作为我国经济增长的主要驱动力[28],其运行情况对货币政策传导有着重要的影响[29],而货币政策的调整可以影响信贷供求,进而对工业经济产生影响[30]。因此,直接分析工业产出和价格对货币供给冲击的影响对经济发展新常态下货币政策的制定和实施,以及在不同情形下工业产出增长对货币供给冲击的响应机制都具有非常重要的现实意义。下文将采用局部投影的方法计算非线性脉冲响应函数,并在工业产出增长、价格变化和货币供给变化的不同区制下,研究我国工业产出和价格在各种不同情形下对货币供给冲击的作用机制,并在此基础上分析新常态前后的货币供给冲击对工业产出和价格的影响,最后根据实证研究结果和相关经济理论进行工业价格对货币供给冲击的情景设计,并给出情景设计下工业产出对货币供给冲击的响应。
2 基于局部投影的冲击模型与置信区间
下文介绍Jorda[11]提出的局部投影方法来计算脉冲响应函数,该方法在计算非线性和非对称脉冲响应方面具有显著优势。
2.1 广义脉冲响应和线性局部投影
脉冲响应函数通常是将诸如VAR模型的线性多变量模型进行Wold分解,并对模型进行估计,然后利用估计值去求得脉冲响应,但前提条件是该模型能够准确表述模型中的数据生成过程,这样求得的脉冲响应才能真实地反映冲击的响应。Koop等[12]和Potter[13]认为脉冲响应函数即使在数据生成过程未知,Wold分解不存在的情况下,依然可以定义成如下的形式:
Φ(t,h,di)=E(yt+h|vt=dt;Xt)-E(yt+h|vt=0;Xt)
(1)
其中,h=0,1,2,…H表示脉冲响应期数;E(.|.)代表最优均方误差;yt是n×1的随机向量;Xt≡(yt-1,yt-2,…)′;0是n×1的零向量;vt是n×1维简化式扰动项;D是n×n的矩阵,其中列向量di表示冲击的大小。一般来说,时间能反映yt中变量动态因果关系的纵向联系,却不能识别同期横向的因果关系。因此,VAR类模型常常对yt中的元素设定一个Wold顺序来对简化式模型残差的方差协方差矩阵进行三角分解,即Ω=PP′。因此,可以定义一个实验矩阵D=P-1,其中矩阵D中的列向量di表示对yt中的第i个元素的结构式冲击。
方程 (1) 计算脉冲响应的统计目标是获取多步最小均方预测误差,当模型能正确表述其数据生成过程时,这个目标可以通过对估计模型的递归迭代来实现。多步预测可以通过对每个预测期的直接预测来实现,因此可以考虑将yt+h投影到由(yt-1,yt-2,…,yt-p)′产生的线性空间中,即:
(2)

(3)
2.2 脉冲响应函数的置信区间
将上述n个时间序列向量yt的所有h=1,2,…,H期的脉冲响应堆叠成一个矩阵,可表示为:
(4)
其中,Φ(1,H)是nH×n的矩阵,且第i个变量对第j个变量的第h期脉冲响应就是n×n矩阵Φh的第(i,j)元素。在简化式中,Φ0=In是非随机的;而在结构识别系统中,Φ0表示yt中元素的同期对应关系,且可以通过设定一定的条件来实现和Φh(h=1,2,…,H) 正交。因此,在不失一般性的假设下,下文不考虑Φ0,仅使用Φ(1,H)表示所有的脉冲响应。
2.2.1 边际置信区间

(5)

(6)
其相应的t比值统计量为:
(7)
在给定假设(5)的情形下,上述统计量可以看作是渐近标准正态分布的。其中,zα/2表示标准正态分布在100(1-α)%的置信水平下的临界值,上述统计量也可以检验如下的原假设,即:
H0:φh(i,j)=0
(8)
因此,在假设(5)正确的前提条件下,式(6)中所表述的边际置信区间是可以用来检验式(8)中零假设是否正确。
2.2.2 Scheffé联合置信区间
在使用脉冲响应时,通常更加注重其冲击路径的形态,而不是仅仅关注某个脉冲响应系数的特定值。因此,可以采用如下原假设来检验脉冲响应函数形态,即:
H0:g(Φ(i,j))=g0
(9)
其中φ(i,j)表示第(i,j)个元素的第1到第H期的脉冲响应函数;g0是一个k×1的可能脉冲响应路径向量,g(.)是在H→k(k≤H)上的1阶可微函数,且其H×k可逆Jacobian矩阵为G(.)。
因此,在式(5)中的高斯假设下,式(9)的原假设可以通过如下的统计量来检验,即:
(10)

(11)

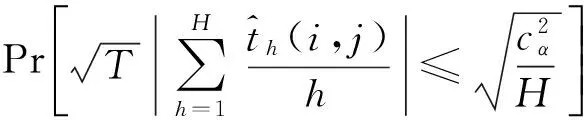
(12)

2.2.3 条件置信区间

(13)
其中,Aij是主对角线元素均为1的下三角矩阵,Dij是对角矩阵。因此,在脉冲响应函数存在序列相关的情形下,检验原假设(8)的Wald统计量在Cholesky分解的基础上可以表示为:
(14)
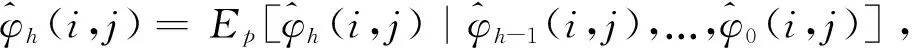
(15)
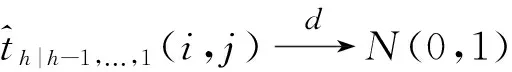
(16)
其中iH是H×1维数值均为1的向量。Scheffé置信区间可以通过式(16)和Cholesky分解计算得到,但是由于脉冲响应存在序列相关,Scheffé置信区间所包含的脉冲响应轨迹可能小于置信水平α,因此扇形概率图表示置信水平会更好些。
最后,每个脉冲响应系数的条件不确定性可以通过构建如下的边界来刻画每个脉冲响应系数的条件不确定性,即条件置信区间可以表示为:
(17)
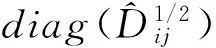
3 新常态下货币供给对我国工业产出和价格冲击的实证研究
下文的实证研究中,首先根据工业产出增长率、工业价格增长率和货币供给增长率序列的门限值,在其高低不同的区制内分析货币供给冲击对工业产出和价格变化的影响;然后分析新常态前后货币供给冲击的影响有怎样的差异;最后,根据我国工业经济的走势和上述分析中货币供给冲击在不同区制和新常态前后的表现,给出新常态下货币供给对工业价格冲击的可能路径,并在此基础上分析经济新常态下,工业产出增长率对货币供给冲击的可能响应,并进行反事实检验。
本文选取1996年10月至2016年5月,共236个样本点的规模以上工业企业增加值 (IP) 当月同比实际增速、工业生产者出厂价格指数 (PPI),以及货币供给和准货币 (M2) 的期末同比增速来分别表示我国工业产出增长率、工业价格增长率 (PPI-100) 和货币供给增长率,如图1所示。
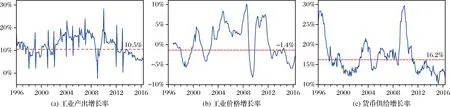
图1 工业产出增长率、工业价格增长率与货币供给增长率的时间序列图数据来源:中经网统计数据库 (http://db.cei.gov.cn/)。
表1给出了三个变量的描述性统计和单位根检验结果,从表中首先可以看出工业产出和价格虽然均值相比货币供给增长率要小,但是最大值和最小值,以及标准差所显示出的波动幅度都大于货币供给增长率。其次,偏度、峰度和J-B统计量显示我国工业产出增长率序列是一个接近于正态分布的序列,而工业价格增长率和货币供给增长率都不是正态分布,其中货币供给增长表现出较为明显的尖峰和右偏的特征。最后,三个序列的单位根检验都很显著,说明三个变量均是平稳的时间序列。
3.1 货币供给冲击的脉冲响应
使用传统VAR模型计算脉冲响应函数时,需选用Akaike的AIC准则、Schwarz的SIC准则和修正的AIC准则 (下面用AICc表示) 来确定线性VAR(p) 模型的滞后阶数,其中AICc准则是Hurvich和Tsai[33]为确定VAR模型的滞后阶数而对AIC准则进行的修订,其在确定VAR模型的滞后阶数方面,具有比AIC和SIC更为稳定和可靠的优势。当选定最大滞后阶数为12个月时,AIC和AICc的结果均表明VAR模型应该选取滞后阶p=4,而SIC的结果表明VAR模型应该选取滞后阶p=2;若将最大滞后数设定为24个月,AICc准则和SIC准则所选择的最优滞后阶数的结果保持不变,认为VAR模型仍分别选取p=4和p=2的滞后阶数,而AIC准则的结果都表明VAR模型应该选取p=13的滞后阶数。若将最大滞后阶数分别设定为36和48时,根据AICc准则确定的滞后阶数均是p=4,SIC准则选取滞后阶p=2,而AIC准则倾向于选择所设定的最大滞后阶数。综合以上结果,本文最终确定滞后阶数为p=4。此外,文中还使用了标准的Cholesky分解,且分解顺序为yt、πt和mt,采用VAR模型和局部投影方法计算工业产出和价格对1倍标准差的货币供给冲击的脉冲响应如图2所示。

表1 序列统计描述和单位根检验
注:"***",“**”,“*”分别表示在1%、5%和10%的显著性水平下显著。
数据来源:作者利用EViews软件计算。

图2 局部投影和VAR模型计算的货币供给冲击下的脉冲响应数据来源:作者绘制。
首先,从图2中可以看出局部投影方法计算出的脉冲响应函数比VAR模型的结果更加敏感,虽然货币供给冲击的脉冲响应具有大致相同的变化趋势,但是局部投影方法计算得到的脉冲响应的大小和波动幅度均显著大于VAR模型,这主要是因为局部投影的方法是对每期脉冲响应都进行不同的估计,得出不同的系数,其脉冲响应函数出现较大的波动也是应有之意。而且从三种不同的置信区间来看,Scheffe置信区间最大,边际置信区间次之,条件置信区间最小,且工业产出对货币供给冲击响应的边际置信区间和条件置信区间相差不大,说明该脉冲响应的序列相关较小。鉴于序列相关对置信区间的显著影响,下文仅给出脉冲响应的条件置信区间。
其次,从局部投影方法的脉冲响应及其条件置信区间来看,工业产出对货币供给冲击的响应在大部分时间内都是显著不为零的,且在第11、13和24期的脉冲响应有显著增大的趋势,这表明工业产出在年初岁尾对货币供给冲击有更为显著的响应,这与我国因节假日而导致的工业产出季节性变化有关,但是总体趋势的先升后降与冯春平认为货币政策冲击在短期会对实体经济部门产生影响,但在长期不会对实体经济部门产生影响的结论基本一致[18];而货币供给冲击对工业价格的影响及其条件置信区间显示,货币供给冲击对工业价格变化有显著的正向冲击,且与VAR模型所得的结果不同,局部投影得到的结果在货币供给冲击1年后非但没有下降,而且还出现了显著的上升,说明局部投影所测度的货币供给冲击对工业产出价格的影响具有较长的持续性,货币供给与工业价格增长率趋势之间存在长期的正向相关关系,不存在货币冲击在短期造成价格反向运动的“价格之迷”的现象,这与刘金全等[34]和陈望远等[35]的结论基本吻合。
最后,图中还给出了根据式(10)对式(9)进行的联合检验和累计检验,其中联合检验的原假设是所有H期脉冲响应的值均为零,累计检验的原假设是H期累计的脉冲响应为零。从检验结果来看,不能拒绝所有H期脉冲响应的值均为零的联合假设,而累计检验认为货币供给对工业产出和价格的累计冲击显著不为零,说明货币供给总的冲击是有效的,但是具体到每个时期其作用效果却存在不确定性。
3.2 货币供给冲击的门限效应
为了研究货币供给政策冲击非对称性,利用Hansen[36]的门限效应检验方法分别确定工业产出增长率、工业价格增长率和货币供给增长率的门限值,并分析在不同区制下,工业产出和价格对货币供给冲击的非线性和非对称响应。具体地,检验变量门限效应的回归方程如下:
(18)

本文参照Jorda[11]的处理方法,利用单个解释变量测度门限变量的门限值,再从结果中挑选出显著性最高的变量,然后将其平均得到门限变量的最终门限值,如在检验工业产出增长率的门限值时,从解释变量工业产出增长率中没有得出明显的门限值,从工业价格增长率这个解释变量中得出最显著的门限值为10.06%,从货币供给增长率这个解释变量中得出最显著的门限值为11%,则最终获取工业产出增长率的门限值为10.5%;同理,可得到工业价格增长率的门限值为-1.4%,货币供给增长率的门限值为16.2%。图1中已经标注出相应的门限值,低于门限值的区域为“低区制”,高于门限值的区域为“高区制”。限于文章篇幅所限,文中没有给出门限效应的检验结果,感兴趣的读者可向作者索取。
3.2.1 工业产出增长不同区制下货币冲击对工业产出和价格影响
确定了工业产出增长率、工业价格增长率和货币供给增长率的门限值后,本文将依据某一变量的门限值将三组数据划分为高、低两个区制,并在不同区制下,分别计算工业产出和价格对货币冲击的响应。
首先,本文将所有变量按照工业产出增长率的门限值δ=10.5%,将数据分成高、低两个区制,并利用局部投影的方法计算工业产出增长率在全样本、高区制和低区制的情形下,工业产出和价格对货币供给冲击的响应,图3给出了三种情形下局部投影计算出的脉冲响应函数,其中两条虚线表示在全样本情形下脉冲响应函数的条件置信区间。
图3显示在工业产出高增长区制,货币供给冲击对工业产出和工业价格的影响与全样本情形下的影响基本趋势一致,但是在大小上还存在一定的差异。具体地,图3(a)显示在工业产出高增长区制下,工业产出对货币供给冲击的响应是正向的,且有逐渐减弱和不显著的趋势,但是累计响应的检验还是显著的,说明在工业产出高增长区制下,货币供给冲击对工业产出总体上存在正向影响;图3(b)中则显示在工业产出高增长率区制内,货币供给冲击对工业产出价格的影响先逐步上升到第8期的0.4,然后下降至第9期的0左右,再上升到第24期的1左右,且累计检验的P值表明累计脉冲响应显著不为零,说明在工业产出高增长率区制内,货币供给冲击对工业价格具有显著的持续影响,宽松的货币供给政策会造成工业价格的显著上升。
从图3还可以看出,在工业产出低增长区制,无论是工业产出,还是工业价格,对货币供给冲击的响应均相对较小,且都是围绕着零值上下波动。该区制下的联合检验和累计检验(图中括号内的数值所示低增长区制下的检验P值,下文类同) 均没有拒绝单个脉冲响应和累计脉冲响应为零的原假设,说明在工业产出低增长的区制内,货币供给冲击对我国工业产出和价格的影响较小,且不显著。此时采用宽松货币供给政策刺激工业经济将不会收到较为理想的效果,因此在工业经济增速下滑的工业经济新常态下,采用货币供给政策刺激工业经济的效果可能不太明显,应当着重从技术进步和产业结构升级等方面挖掘工业经济供给侧的新动力[28]。

图3 工业产出和价格增长率对货币供给冲击的脉冲响应 (门限变量:工业产出增长率)数据来源:作者绘制。
3.2.2 工业价格增长不同区制下货币冲击对工业产出和价格影响
同样,将数据按照工业价格增长率的门限值δ=-1.4%分成高、低工业价格增长率两个区制,并利用局部投影的方法计算工业产出和价格在全样本、高区制和低区制的情形下对货币供给冲击的响应,图4给出了三种情形下局部投影计算出的脉冲响应函数。
从图4中可以看出,在工业价格高增长区制下,工业产出对货币冲击的脉冲响应出现显著的先升后降的态势,这说明在工业价格高增长区制下,货币供给冲击对工业产出仅有短期影响,且累计检验显示这种影响不存在长期性。但是,工业价格对货币供给冲击的脉冲响应则显示出较为稳定的特征,虽然在形态上呈现出周期性波动,但是总体上来说,工业价格在其高增长区制下对货币供给冲击的累计响应是显著不为零的。图4中还显示在工业价格增长率的不同区制下,尤其是在工业价格低增长的区制下,货币供给对工业产出和价格增长率的冲击相对较小,均在零值上下变化,且无论是联合检验还是累计检验的P值均不显著,即接受在工业价格低增长率的区制下货币供给冲击无效的假说。因此,图1(b) 的结果表明当前工业价格出现通缩的情形下[37],不适宜采取货币供给冲击来刺激工业经济,而事实上我国宏观政策也确实是这么调控的,货币供给一直处于低水平增长,如图1(c) 所示。

图4 工业产出和价格增长率对货币供给冲击的脉冲响应 (门限变量:工业价格增长率)
3.3 新常态前后工业经济对货币供给冲击的非对称响应
当前,我国经济正处于从“旧常态”向“新常态”过度的深度调整期[38],工业增速和增长动力都发生着重大转变。刘伟和蔡志洲[39]认为我国工业经济在2010年前后步入了工业化后期;赵昌文等[40]认为自2012年前后我国经济进入工业化后期,经济发展进入新常态;金碚[41]认为我国经济基本面自2011年开始发生历史性的实质变化,经济发展进入新常态,这说明我国工业经济进入新常态没有一个确切的时间。实际上,从图1(a) 可以看出我国工业产出增长率自2010年开始就出现了急速下滑的趋势,虽然在2012和2013年的年初岁尾出现了反复,但是仍然改变不了这个趋势。根据金碚[41]的表述和文中门限值的结果,将2011年作为我国工业经济新常态的分界点,并据此将样本数据划分为旧常态和新常态两个区间,并采用局部投影分别计算新常态前后工业产出和价格对货币供给冲击的脉冲响应如图5所示。
从图5(a) 中工业产出在新常态前后对货币供给冲击的响应可以看出,旧常态时期的脉冲响应比全样本所得到的脉冲响应要小,但基本形态类似。但是在新常态下的脉冲响应的波动幅度是最大的,而且在形态上与全样本和旧常态下的脉冲响应有较大差异,不仅在多处出现了负值,而且变化幅度也在逐步加大,这说明在经济发展新常态初期,我国工业经济增长率正从一个高速增长阶段向中高速增长阶段进行转变,此时货币供给政策作用的效果存在显著的不确定性,此时需要谨慎使用货币供给政策来刺激经济的增长,保持现有的稳健性货币供给政策不失为一个好的选择。图5(b)中工业价格在新常态前后对货币供给冲击的响应存在显著不同,与图5(a)类似,旧常态下的工业价格增长率对货币供给冲击的响应与全样本情形下的脉冲响应有基本相同的走势,但是响应的系数要小;而在新常态下,工业价格增长率对货币供给冲击的响应在前10个季度出现大幅上扬,随后逐渐回落至零左右,这说明新常态下货币供给政策作用的短期效果特别明显,长期作用效果基本趋于零,从脉冲响应系数的显著性检验结果看 (括号里面是新常态下的检验结果,括号外面是旧常态下的检验结果),仅在10%的显著性水平和新常态下,货币供给对工业价格增长率的累计冲击显著不为零。以上结果说明经济发展新常态下,增加货币供给的货币政策冲击有助于刺激工业经济的活性 (工业产出波动剧烈,工业价格短期大幅上扬),但是若将其作为一种拉动工业经济增长的主要手段,其长期作用效果却得不到保证,这对我国经济新常态下货币供给政策制定和实施具有重要的参考意义。
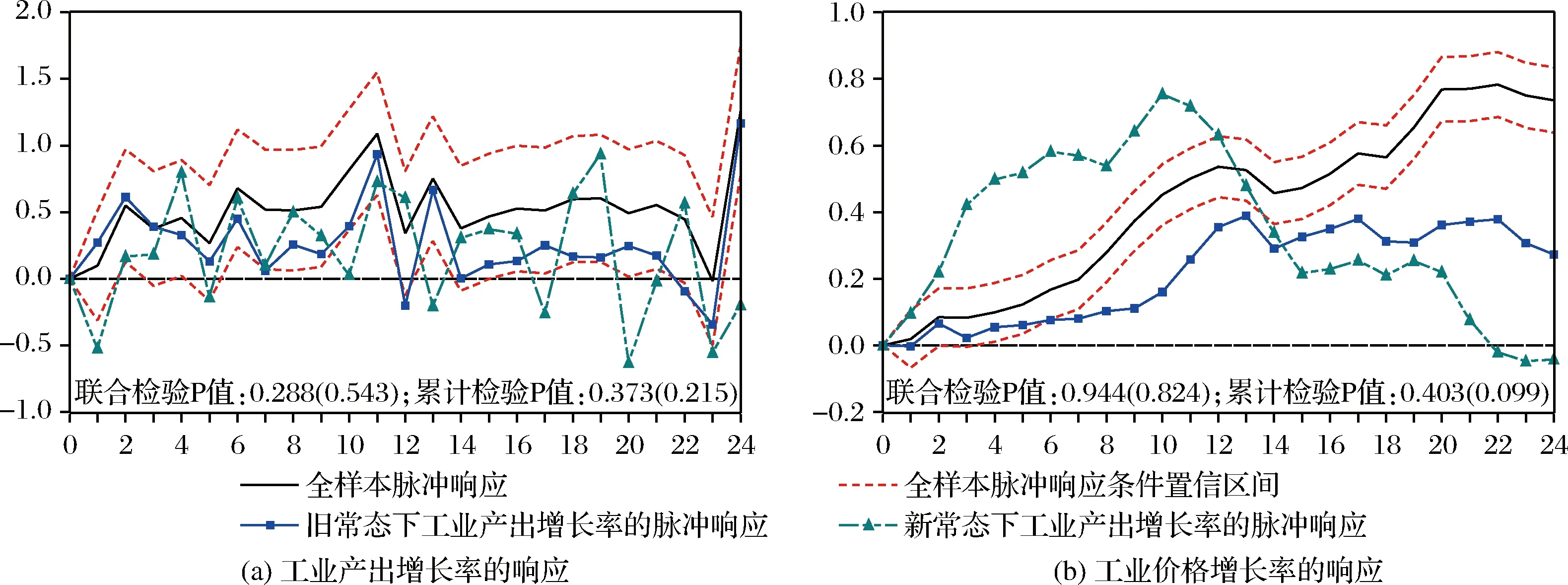
图5 新常态前后工业产出和价格增长率对货币供给冲击的脉冲响应数据来源:作者绘制。
3.4 经济发展新常态下的情景设计与反事实检验
虽然上述分析已经给出了货币供给冲击对工业产出和价格增长率影响的非对称性和阶段性的重要启示,但是本文更加关注在新常态下,工业产出将会对货币供给冲击产生怎样的一种影响。因此本文将在工业价格对货币供给冲击的响应路径上,施加一种路径约束进行情景设计,分析情境设计下的工业产出对货币供给冲击的响应,并进行反事实检验分析情景设计的真实性[25, 32]。
根据经济理论和实证研究,可以针对某一脉冲响应路径进行情景设计,如将变量k对变量l的冲击路径约束为φc(k,l),则在(5)式的假设条件下,所有其他脉冲响应φ(i,j) (i,j∈{1,...,n},i≠k,j≠l) 在情景设计下的局部投影值可表示为:
(19)
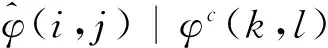
由于上式中右边第二项是一个半正定的矩阵,因此情景设计下的协方差矩阵的迹比原来的要小,这主要是因为使用了一个已知的冲击路径φc(k,l)代替了原来的未知冲击路径φ(k,l)。
因此,可以采用标准的Wald统计量来检验情景设计的真实性,即原假设为H0:φ(k,l)=φc(k,l)的反事实检验可表示为:
(21)
基于上述思想和前文所做的实证分析,本文设计两种可能情景,其中第一种情景是基于货币供给冲击对工业价格有长期影响而设计的;第二种情景是基于货币供给冲击对工业价格仅有短期影响,而无长期影响进行设计的,具体情景设计和分析结果如下文所示。
3.4.1 情景一:工业经济持续低迷,工业价格对货币供给冲击的响应减半
从图1(a)中可以看出我国工业产出增长率从后金融危机时期就开始进入了下滑趋势的通道中,门限效应结果显示其自2012年就处于低增长区制,此时我国经济发展也进入新常态。而图1(b)也显示此时我国工业价格处于低增长区制。此外,从图3(b)和图4(b)中货币供给冲击对工业价格的影响可以看出,若工业经济持续低迷,工业价格对货币供给冲击响应将如图6(b)一样大小减半,该情景设计的反事实检验P值为0.998,即不能拒绝情景设计下的脉冲响应路径与实际脉冲响应路径相等的原假设,说明情景设计是可能产生的。在此情景下,货币供给冲击虽然仍旧对工业产出有着长期持续的影响,但是其影响程度要小得多;工业产出对货币供给冲击的响应和原始脉冲响应有着相同的趋势,但是脉冲响应的幅度要小,且不是原始脉冲响应的简单减半。譬如:在脉冲响应开始时,其响应幅度和原来脉冲响应相差不多,随后却又呈现出慢慢扩大的趋势,但是在第11、13和第24期这种差距又相对较小,且这几期的响应系数均显著。这说明在经济新常态下,若工业经济 (包括价格和产出) 持续低迷,货币供给冲击对工业价格影响减半的情形下,工业产出对货币供给冲击的响应仍旧为正,且有所降低,但却不是简单的减半,采用货币供给刺激经济增长没有显著效果。

图6 情景一下工业产出和价格对货币供给冲击的脉冲响应
3.4.2 情景二:基于实证分析结果,工业价格对货币供给冲击的响应先升后降
从图5(b) 中新常态下工业价格对货币供给冲击的响应路径来看,均呈现一种先升降的趋势,即表明货币供给冲击对工业价格的短期影响逐渐上升,但在长期影响却逐渐下降。据此,本文设计如图6(b) 所示的情景二,即工业价格对货币供给冲击的响应呈现先升再缓降的形态。从情景二的反事实检验P值为0.768可以看出情景二的设计是较为合理的,有现实根据和未来出现的可能。在此情景下,货币供给冲击对工业产出的影响在最初7期,基本上与无情景设计下的脉冲响应没有太大的区别,且从其条件置信区间可以看出这些期脉冲响应系数的显著性有了些许提高。但是从第8期开始,工业产出对货币供给冲击的响应比无情景设计时要小,且有扩大的趋势。这说明我国新常态下货币供给冲击对工业产出的影响短期内不会发生变化,但是长期影响和累计响应都将发生重大变化,货币供给冲击的长期效应减弱,甚至是无效用都是很有可能发生的。情景二说明经济新常态下,采用货币供给政策刺激工业经济增长的作用效果在短期有一定的作用,但是从长期来看,其作用效果将显著减弱且不显著。

图7 情景二下工业产出和价格对货币供给冲击的脉冲响应
4 结语
本文采用局部投影的方法计算货币供给冲击在工业产出增长率、工业价格增长率和货币供给增长率的不同区制下,以及新常态前后对工业产出和价格的非对称影响,并在上述实证和相关理论的基础上提出了新常态下货币供给冲击对工业价格影响的两种情景设计方案,并在情景中分析了货币供给冲击对工业产出的影响。通过以上分析,本文得出了以下几点结论:
第一,局部投影方法计算的脉冲响应函数与传统VAR模型计算的脉冲响应函数相比,该模型改进了对模型正确设定的过度依赖,即VAR模型无法正确反映数据生成过程时,其所计算的脉冲响应的误差会越来越大的问题,这对因VAR模型设定偏误所造成的脉冲响应路径的偏差是个非常重要的改进,但是由于局部投影对每期参数值进行估计,其脉冲响应的结果和传统VAR模型相比,必然会有较大的波动。此外,局部投影的条件置信区间改进了传统的脉冲响应函数中因序列相关而造成置信区间估计不合理的问题,Sheffee置信区间能够包含各期投影脉冲响应的未来所有可能路径,这对脉冲响应的置信区间是个重要的改进。
第二,在工业产出增长率,工业价格增长率和货币供给增长率的不同区制下,使用局部投影的方法研究货币供给冲击对工业产出和工业价格的非对称影响,本文发现货币供给冲击对工业产出的影响无论是在高增长区制,还是在低增长区制,其影响都存在较大的不确定性,仅在脉冲响应的个别期存在显著的正向影响,脉冲响应的各期影响均为零的联合检验和累计影响为零的累计检验均不能够拒绝原假设,说明货币供给对工业产出增长率的总体影响和累计影响不显著,即货币供给冲击对工业产出的长期影响表现出中性的特征。然而,货币供给冲击对工业价格不仅表现出显著的正向影响,还体现出了明显的非对称特征,其中在工业产出和价格高增长区制内,以及货币供给低增长区制内,货币供给冲击对工业价格的影响要显著大些,且其联合检验和累计检验的结果均更为显著,表现出明显正向影响和非对称特征。
第三,文中将样本划分为新常态和旧常态,并在两个样本区间内比较分析货币供给冲击对工业产出和价格的影响。研究表明,新常态前后货币供给冲击对工业产出的影响与门限效应下的货币供给冲击的影响类似,均是在个别响应期显著,在整体和累计冲击上表现出中性的特征;而货币供给冲击对工业价格的影响在新常态前后则表现出明显的差异和非对称性特征,尤其是在新常态下货币供给冲击出现先升后降的特征,体现出了货币供给冲击对工业价格的影响短期有效,长期无效的特征,而且联合检验不显著,累计检验显著的结果也证实了上述结论。
第四,根据货币供给冲击在工业产出和价格增长率的不同区制下,对工业价格的影响,本文设计了工业经济持续低迷下,工业价格对货币供给冲击响应减半的情景一;根据货币供给增长率不同区制下和新常态前后,货币供给冲击对工业价格增长率影响的实证结果,设计了工业价格对货币供给冲击的响应呈现先升后降的情景二。基于上述两种工业价格对货币供给冲击的响应路径的情景设计分析结果,可以看出新常态下我国货币供给冲击对工业产出的影响主要表现在短期,且影响具有不确定性。但是从长期来看,这种影响会逐渐降低,甚至会出现负增长。这说明,在经济发展新常态下和工业经济低迷的情形下,应该从工业内生动力机制的改善上来谋求工业经济增长,而依赖诸如货币供给增长的外在冲击的拉动,工业产出增长只能获得短期的效果,无法获得持续的动力,反而会导致工业价格的剧烈变化,工业经济将出现更加不可预料的后果。
总之,局部投影方法的脉冲响应分析认为货币供给冲击对工业产出的影响具有不确定性的特征,仅在个别期的脉冲响应显著,总体上表现为中性特征,情景分析也证实了上述结论。而货币供给冲击对工业价格的影响则相对较大,不仅表现出门限效应下的非对称性,还在新常态前后表现出显著的差异性,总体表现为短期有效,长期无效的特征。因此,在工业经济新常态和工业经济持续低迷的情形下,采用货币供给政策来刺激工业经济是不可取的,其对工业产出增长的影响具有非常大的不确定性,但是却对工业价格增长率产生积极的正向影响,即有可能出现工业产出停滞不前,而工业价格急剧飙升的工业滞胀的情形出现。因此,需要从工业产业升级,工业技术的创新等工业供给侧理顺工业内生动力机制,寻求工业经济新的增长点。
[1] 程方楠, 孟卫东. 宏观审慎政策与货币政策的协调搭配——基于贝叶斯估计的DSGE模型[J]. 中国管理科学,2017,25(1):11-20.
[2] Bagliano F C, Favero C A. Measuring monetary policy with VAR models: An evaluation[J]. European Economic Review,1998,42(6):1069-1112.
[3] Ball L, Mankiw N G. Asymmetric price adjustment and economic fluctuations[J]. The Economic Journal,1994,104(423):247-261.
[4] Christiano L J, Eichenbaum M, Evans C L. Identification and the effects of monetary policy shocks[M]// Blejer M I, Eckstein Z, Hercowitz Z, et al. Financial factors in economic stabilization and growth. Cambridge: Cambridge University Press,1996:36-74.
[5] Evans C L, Marshall D A. Monetary policy and the term structure of nominal interest rates: Evidence and theory[J]. Carnegie-Rochester Conference Series on Public Policy,1998,49:53-111.
[6] Sims C A. Interpreting the macroeconomic time series facts[J]. European Economic Review,1992,36(5):975-1000.
[7] 刘斌. 货币政策冲击的识别及我国货币政策有效性的实证分析[J]. 金融研究,2001,(7):1-9.
[8] Karras G. Are the output effects of monetary policy asymmetric? Evidence from a sample of European countries[J]. Oxford Bulletin of Economics and Statistics,1996,58(2):267-278.
[9] Senda T. Asymmetric effects of money supply shocks and trend inflation[J]. Journal of Money, Credit and Banking, 2001, 33(1): 65-89.
[10] Sims C A. Macroeconomics and reality[J]. Econometrica, 1980, 48(1): 1-48.
[11] Jorda O. Estimation and inference of impulse responses by local projections[J]. The American Economic Review, 2005, 95(1): 161-182.
[12] Koop G, Pesaran M H, Potter S M. Impulse response analysis in nonlinear multivariate models[J]. Journal of Econometrics, 1996, 74(1): 119-147.
[13] Potter S M. Nonlinear impulse response functions[J]. Journal of Economic Dynamics and Control, 2000, 24(10): 1425-1446.
[14] Weise C L. The asymmetric effects of monetary policy: A nonlinear vector autoregression approach[J]. Journal of Money, Credit and Banking, 1999, 31(1): 85-108.
[15] Assenmacher-Wesche K. Estimating central banks’ preferences from a time-varying empirical reaction function[J]. European Economic Review, 2006, 50(8): 1951-1974.
[16] Lütkepohl H, Teräsvirta T, Wolters J. Investigating stability and linearity of a german M1 money demand function[J]. Journal of Applied Econometrics, 1999, 14(5): 511-525.
[17] Christopoulos D K, Leon-Ledesma M A. A long-run non-linear approach to the Fisher effect[J]. Journal of Money, Credit and Banking, 2007, 39(2-3): 543-559.
[18] 冯春平. 货币供给对产出与价格影响的变动性[J]. 金融研究, 2002, (7): 18-25.
[19] 赵进文, 闵捷. 央行货币政策操作效果非对称性实证研究[J]. 经济研究, 2005, (2): 26-34+53.
[20] 赵进文, 黄彦. 中国货币政策与通货膨胀关系的模型实证研究[J]. 中国社会科学, 2006, (2): 45-54+205-206.
[21] 刘金全, 郑挺国. 我国货币政策冲击对实际产出周期波动的非对称影响分析[J]. 数量经济技术经济研究, 2006, (10): 3-14.
[22] 彭方平, 王少平. 我国货币政策的微观效应——基于非线性光滑转换面板模型的实证研究[J]. 金融研究, 2007, (9): 31-41.
[23] 郑挺国, 刘金全. 我国货币—产出非对称影响关系的实证研究[J]. 经济研究, 2008, (1): 33-45.
[24] 刘金全, 隋建利, 李楠. 基于非线性VaR模型对我国货币政策非对称作用效应的实证检验[J]. 中国管理科学, 2009,17(3):47-55.
[25] 刘汉, 刘金全. 中国宏观经济情境设计与路径预测[J]. 中国管理科学, 2013,21(1): 47-56.
[26] 刘金全, 隋建利, 闫超. 中国实际产出增长率及其不确定性中的长期记忆性和相关性测度[J]. 社会科学战线, 2010,21(1):47-55.
[27] 汤丹. 基干svar模型的中国核心通货膨胀估计及预测评价研究[J]. 宏观经济研究, 2015, (1): 109-115.
[28] 黄群慧. “新常态”、工业化后期与工业增长新动力[J]. 中国工业经济, 2014, (10): 5-19.
[29] 田奇. 从工业经济运行看货币政策传导衰减成因[J]. 当代经济, 2000, (8): 30-31.
[30] 刘海英, 何彬. 工业增长、信贷供求和货币政策调整[J]. 中国工业经济, 2009, (7): 5-15.
[31] Scheffe H. A method for judging all contrasts in the analysis of variance[J]. Biometrika, 1953, 40(1-2): 87-110.
[32] Jorda O. Simultaneous confidence regions for impulse responses[J]. Review of Economics and Statistics, 2009, 91(3): 629-647.
[33] Hurvich C M, Tsai C-L. A corrected Akaike information criterion for vector autoregressive model selection[J]. Journal of Time Series Analysis, 1993, 14(3): 271-279.
[34] 刘金全, 张文刚, 刘兆波. 货币供给增长率与通货膨胀率之间的短期波动影响和长期均衡关系分析[J]. 中国软科学, 2004, (7): 39-44.
[35] 陈望远, 李仲飞, 黄金波. “中国货币之谜”:事实还是假象[J]. 中国经济问题, 2012, (4): 32-41.
[36] Hansen B E. Sample splitting and threshold estimation[J]. Econometrica, 2000, 68(3): 575-603.
[37] 龙少波, 胡国良, 王继源. 国际大宗商品价格波动、投资驱动、货币供给与PPT低迷——基于TVP-VAR-SV模型的动态分析[J]. 国际金融研究, 2016, (5): 3-14.
[38] 黄群慧, 原磊. 步入“新常态”的工业经济运行:发展特征与未来趋势[J]. 区域经济评论, 2015, (3): 24-33.
[39] 刘伟, 蔡志洲. 我国工业化进程中产业结构升级与新常态下的经济增长[J]. 北京大学学报:哲学社会科学版, 2015, 52(3): 5-19.
[40] 赵昌文, 许召元, 朱鸿鸣. 工业化后期的中国经济增长新动力[J]. 中国工业经济, 2015, (6): 44-54.
[41] 金碚. 中国经济发展新常态研究[J]. 中国工业经济, 2015, (1): 5-18.

