基于顾客不公平规避的服务定价研究

刘 健，赵洪款，刘思峰

(1.南京理工大学经济管理学院，江苏 南京 210094； 2. 南京航空航天大学经济管理学院，江苏 南京 211106)

1 引言

近年来，现代服务业快速发展。2015年，我国服务业继续保持较快增长，服务业增加值占国内生产总值的比重达到50.5%，目前服务业已成为国民经济第一大产业[1]。排队问题的研究对于服务质量的提升至关重要，排队源于短时间内供给与需求的不匹配，因而根据相关排队问题设计有效的排队机制可以辅助服务资源的有效配置。排队问题涉及医疗机构[2]、呼叫和通信中心[3]、计算机网络[4]、银行排队服务[5]、集装箱集卡预约[6]、维修排队系统[7]等领域。由于顾客的异质性(即：顾客的时间成本不同)，为了提高排队效率和顾客满意度，需要对顾客的异质性进行有效区分[8]。目前服务商通常采用在服务系统中设置优先权(贵宾席)的方式对顾客进行分类服务来实现对顾客异质性的区分。

分类服务的实质是对顾客等待时间的重新分配，大量的实践调研和研究发现，当服务系统中的普通顾客察觉或感知到部分顾客因为支付优先服务费用而减少等待时间，心里上会产生不公平感[9]，(顾客的不公平来源于感知与较)。普通顾客的不公平感会引起不同类型服务队列之间的顾客流动或转移，从而影响企业收益和社会成本。其中，企业收益(如：游乐场所、餐饮等)是营利性企业关注的优化目标，社会成本主要是非营利性企业(如：社会福利部门等)关注的优化目标。

本文针对顾客不公平规避偏好行为对于企业收益和社会成本的影响进行研究。接下来从顾客分类(优先权设置)和顾客行为偏好(顾客对于等待时间的偏好和顾客对于公平性的偏好)两个方面进行文献综述。在优先权设置方面，Stanford[10]研究了单服务台系统(M/M/1)中顾客优先服务级别存在多个层次，顾客到达率分别服从泊松分布和一般分布时的顾客等待时间和离开时间。Gavirneni和Kulkarni[11-12]同样以M/M/1为例，基于顾客等待时间为收益函数分布、均匀分布和指数分布，针对顾客不能离开系统和能离开系统两种情形，对企业收益和社会成本优化目标进行研究。Wang Jianfu等[13]分析服从抢占式规则的存在高低两类优先权的M/M/C排队模型，并且重点关注低优先权的排队性能指标。Yang Luyi等[14]研究优先权拍卖的最优的时间交易机制，既可以辅助社会规划者提高系统效率，也可以辅助提高企业收益。上述研究多是集中在顾客理性的和直接可见的排队性能指标上，对于顾客行为因素造成的排队性能指标隐性变化(顾客效用)缺乏考虑，这些变化同样会影响到顾客选择和企业效益。

在排队公平方面，Avi-Itzhak等[18]指出排队公平和广义社会公平的差异以及量化排队公平基本原则：量化指标需符合广义社会公平的概念，粒度，具有直觉感官上的说服力和理性。Raz等[19]基于资源分配排队公平度量模型，提出度量排队系统不公平的新指标：类别歧视。Sandmann[20]指出服务质量评估中顾客感知公平性的重要性，并对用来量化不公平性的歧视频率进行改进。闫崇军等[21]考虑公平性约束问题对优化医院排队系统中预约调度问题的影响，利用各个预约时段平均等待时间的差值描述了患者感知的公平性差异。Geng Xin等[22]针对不同性质服务台的内生公平性问题，定义了两个服务台基于比较的不公平函数、自身忙期负效用函数以及总的负效用函数。以上文献考虑排队过程中对比所造成的公平性问题，但是多集中于公平的量化表示，对比所引发的公平性问题对企业效益的影响研究不够深入。

现有文献针对排队问题中顾客行为的研究，主要集中两个方面：①等待时间价值高的顾客(优先权顾客)具有不耐烦性；②不同服务台之间的繁忙程度不同而引起的服务器(或工作人员)之间的不公平；而对于排队系统中顾客的不公平规避偏好并没有给予足够关注，同时也没有关注顾客不公平规避偏好对服务系统的影响。

本文创新之处：围绕垄断型服务系统(某些地区服务产品市场竞争力不强或产品的替代性较弱)中普通顾客的不公平规避心理偏好对企业收益和社会成本的影响进行分析。基于顾客时间价值均匀分布，针对优先权顾客最优比例，获取优先权服务最优定价值，企业最大收益值与社会成本最小值等进行研究，在此基础上，进一步分析上述最优解与顾客不公平规避参数之间的关系。

本文的主要架构：首先，构建顾客存在不公规避情形下新的效用模型，分析顾客效用选择和优先服务支付费用；其次，对企业收益目标函数进行优化分析；然后，对社会成本目标函数进行优化分析；接下来，通过案例利用数值分析和理论推导，进一步对不公规避参数与企业收益与社会成本最优解之间的性质关系进行分析验证；最后，对本文所做的主要工作进行归纳总结，并指出未来的研究方向。

2 模型构建

假设顾客进入服务系统的到达率为λ(泊松分布)，系统的服务率为μ(当λ≥μ，服务系统中的队列长度趋于无穷大，企业收益和社会成本无限大，本文仅考虑λ<μ情形)。假设商家对进入服务系统的顾客收取固定费用c，并同时给出一个选择，如果顾客愿意支付额外的费用K，可以加入一个具有优先权的群体，即：总支付费用为K+c的顾客，相对于仅支付费用为c的顾客具有优先权。优先权的设置使得服务系统中优先权顾客的期望等待时间W1小于(或等于)普通顾客的期望等待时间W2(W2≥W1)。与此同时，普通顾客与优先权顾客之间的等待时间差别会引发普通顾客心里的不公平感。本文将顾客心理上的不公平感觉用参数α表示，显然α≥0。

Larson[23]指出先到先服务(Fist in Fist out, FIFO)是排队机制中最公平的社会判定规则，在排队过程中违背该规则的排队机制会引发顾客的不公平感。基于上述原理与顾客在分类服务排队过程中的对比和感知性，本文利用不同队列之间的期望时间之差W2-W1与顾客的不公规避参数α将普通顾客不公平规避心理引起的负效用表示为α(W2-W1)。显然，当排队系统为FIFO类型时W2=W1=W(此时顾客的不公平规避心理将不再产生负心理效用)。

2.1 效用模型

这里与传统研究的不同之处是，顾客选择进入普通队列后所获得的服务效用不是R'-H·W2-c，因为本文考虑到普通顾客不公平心理引起的负效用，这也是本文的创新之处。

顾客进入服务系统选择成为优先权顾客还是普通顾客，取决于通过两种服务所获得的总体效用大小。从这个角度出发，我们首先考虑其期望等待时间的表达，为了简化模型，本文假设服务系统为垄断型(顾客不能选择离开)，那么优先权与普通顾客等待时间分别[24]为：

(2)

(3)

2.2 效用选择

顾客进入服务系统后，选择进入优先权还是普通队列，是由其进入不同队列获得的总体效用决定的。选择进入优先权队列应满足U1≥U2。

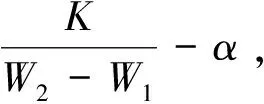
根据上述分析可知不同队列顾客到达率与顾客等待时间价值之间的关系式如下所示：

(4)

其中：λ1为优先权队列顾客的到达率，λ2为普通队列顾客的到达率。按照上面的分析，本文接下来从营利性企业与非营利企业，即：收益最大与社会成本最小两个目标出发分别进行优化分析。

3 营利性企业(企业收益最大化)

根据公式(4)，可得：

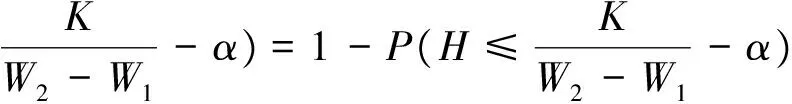
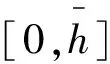
(5)

假设R(θ)(α)为优先权顾客比例为θ，不公规避参数为α时的收益函数，其表达式如(6)所示：

R(θ)(α)=λθ(K(θ)(α)+c)+λ(1-θ)c

(6)

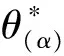
(7)

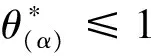
(8)

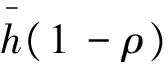
(9)

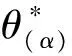
(3)当不考虑顾客的不公平规避偏好，即α=0时，优先权顾客的最优比例、优先服务最优定价值以及企业的最大收益值如式(10)所示：

(10)

针对上面的三种情形，存在下面关系式，

因此服务提供商考虑顾客的不公平规避偏好可以获得更大收益。在垄断型服务系统中，企业应将优先权顾客服务窗口与普通顾客服务窗口设置在互相之间可以看到的位置(Visual-Service System，如登机口)，通过刺激顾客的不公平规避心理，并进一步提高获取优先权服务的费用，来获得更大收益。随着顾客不公平规避偏好的增大，接受优先服务的顾客比例也越大，同时服务提供商可收取更高的优先权服务费用。

接下来将针对非营利性企业，从社会成本最小化角度出发对顾客分类的服务定价进行研究。

4 非营利企业(社会成本最小化)

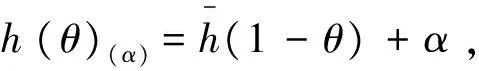
假设C(θ)(α)为优先权顾客比例为θ，不公平规避参数为α时的社会成本函数，其表达式如(11)所示[11]：

(11)

其中：P′(H)表示时间价值H的概率密度，从而可得C(θ)(α)如式(12)所示：

(12)

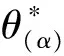
(13)

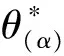
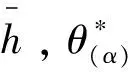
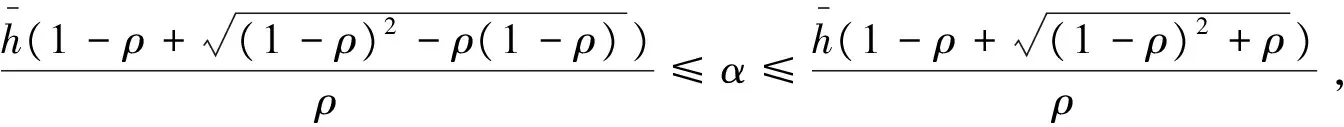
(1)当不公规避参数满足

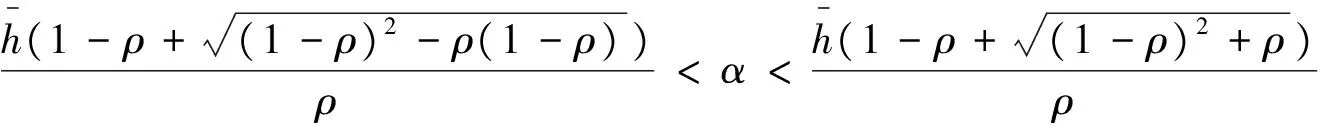
此时进入优先权队列的最优费用(优先服务最优定价值)与社会成本最小值分别为：

(14)

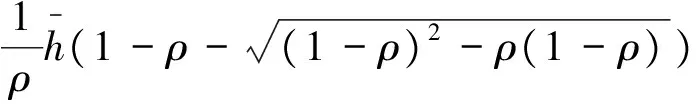
(15)

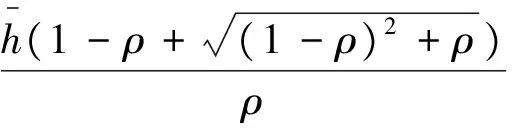
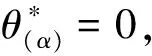
(16)

(4)若不考虑顾客的不公平规避偏好，即α=0时，优先权顾客的最优比例、优先服务最优定价值以及社会成本最小值分别为：

(17)

当顾客的不公平规避偏好较小时，可适当增加优先权顾客比例，当顾客不公平规避偏好较大时，应减少优先权顾客比例或取消顾客分类服务，来减少服务系统产生的社会成本。

接下来我们将对第3和第4部分最优解与顾客公平偏好之间的关系进行分析。

5 最优解性质分析

5.1 营利性企业性质分析

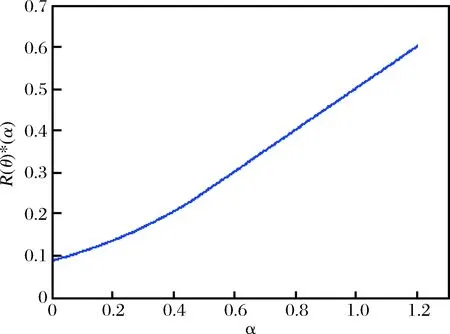
图1 企业最优收益与不公平规避偏好关系

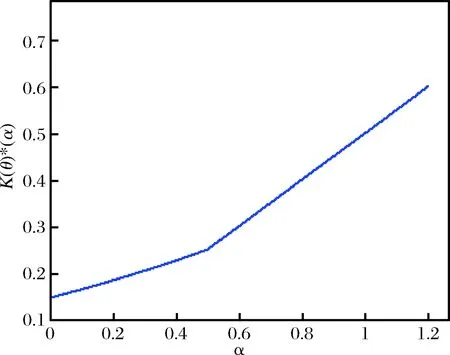
图2 优先服务最优定价值与不公平规避偏好关系

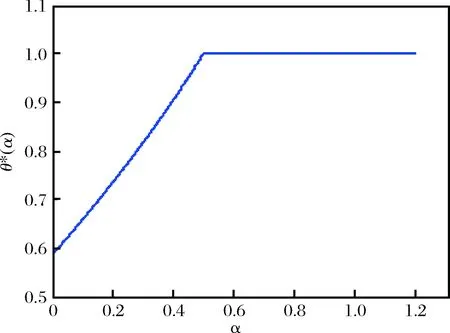
图3 优先权顾客最优比例与不公平规避偏好关系

5.2 非营利性企业性质分析

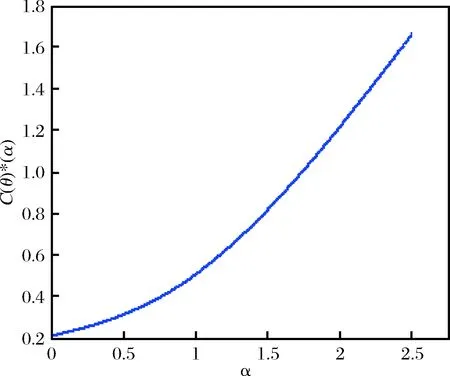
图4 社会最小成本与不公平规避偏好关系

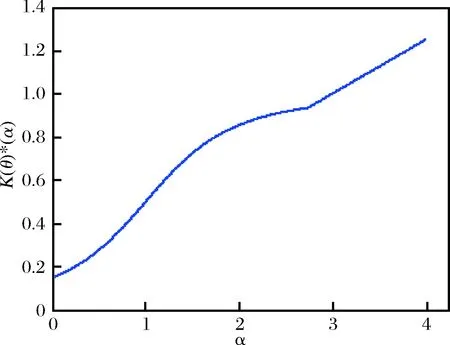
图5 优先服务最优定价值与不公平规避偏好关系

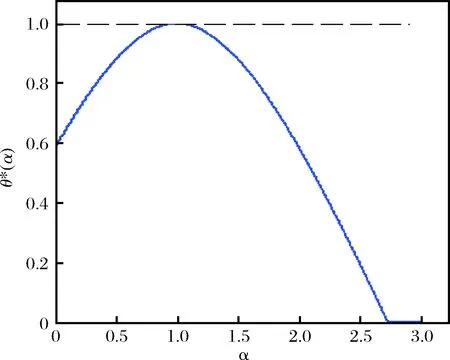
图6 优先权顾客最优比例与不公平规避偏好关系

5.3 性质分析

通过对第3部分和第4部分的最优解进行求导分析可以进一步对相关性质进行讨论：

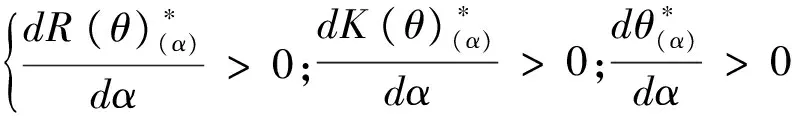
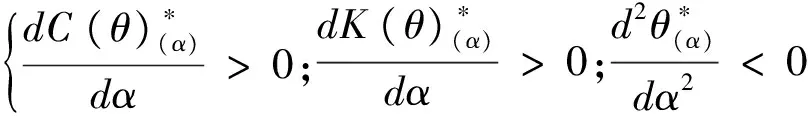
综上所述，针对垄断型服务系统，从社会成本最小或企业收益最大两个目标出发，在考虑顾客公平偏好时，当所有顾客都进入优先权队列，服务商仍然可对顾客收取优先服务费用。从理论上而言，当顾客公平参数α非常大时，顾客优先服务费用可趋于无穷大。

6 结语

本文针对普通顾客排队过程中的不公规避心理对企业收益和社会成本的影响进行研究，通过研究得到了一些有价值的结果。本文主要做了三个方面的工作：①企业收益最大化视角的优先权顾客比例、顾客优先服务费用和企业最大收益值的分析与求解；②社会成本最小化视角的优先权顾客比例、顾客优先服务费用和社会成本最小值的分析与求解；③最优解与顾客不公平规避参数α之间的关系分析。本文研究指出当顾客不公平规避偏好较弱(小)时，从社会成本和企业收益两个视角服务提供商都应对顾客进行分类服务。当顾客不公平规避偏好较强(大)时，从企业收益最大的角度应仅保留优先权顾客，从社会成本最小的角度应取消顾客分类仅保留普通顾客。

针对营利性企业(收益最大化为优化目标)，服务商应该通过收取优先服务费用对顾客进行分类服务，并且将优先权顾客服务窗口设置在普通顾客能够看到的位置以刺激顾客不公规避心理，从而使得更多的顾客通过支付更高的优先权费用获取优先权服务，进而获得更大收益(如普通顾客与VIP顾客登机口排队)。针对非营利性企业(社会成本最小化为优化目标)，当顾客的不公平规避偏好较弱时，服务商应该提供分类服务(收取优先服务费用)并且将优先权顾客服务窗口设置在普通顾客无法看到的位置以减少对于顾客不公规避心理的刺激。这样既可以对顾客异质性进行有效区分提高服务满意度，又可以实现整体社会成本的最优化，医院通常采取这种服务机制；当顾客的不公规避偏好较强时，服务提供商应取消分类服务(只收取普通服务费用，取消优先服务费用)实现整体社会成本的最优化。

本文针对顾客不能离开服务系统的垄断型服务系统进行研究具有一定的应用局限性，现实生活中多数情形顾客可以自由选择离开服务系统，同时也没有考虑服务系统优先权顾客的公平心理对企业收益和社会成本的影响，这些都是我们进一步的研究工作。

[1] 许剑毅. 2015年服务业引领国民经济稳步发展 [EB/OL].[2016-03-10].http://www.gov.cn/xinwen/2016-03/10/content_5051710.htm.

[2] 陈妍,周文慧,华中生,等. 面向延时敏感患者的转诊系统定价与能力规划[J].管理科学学报,2015,18(4):74-83.

[3] Ibrahim R, Armony M, Bassamboo A. Does the past predict the future? The case of delay announcements in service systems[J].Management Science, 2016,63(6):1762-1780.

[4] 程春玲,王颖，张登银. 云计算中基于动态阈值的服务器唤醒策略[J].系统工程与电子技术, 2015,37(6):1438-1445.

[5] 程元军, 罗利. 基于排队论和整数规划的银行柜员弹性排班模型[J]. 管理学报, 2010, 07(10):1558-1565.

[6] 曾庆成, 陈文浩, 胡祥培,等. 集装箱码头外部集卡预约优化模型与算法[J].中国管理科学, 2015, 23(10):125-130.

[7] 徐立, 李庆民, 阮旻智. 具备有限维修能力的舰船编队保障方案优化[J].系统工程与电子技术, 2014, 36(11):2226-2232.

[8] 周文慧, 黄伟祥, 吴永忠,等. 提高顾客等待满意度的两类排队管理策略[J]. 管理科学学报, 2014, 17(4):1-10.

[9] Rafaeli A,Kedmi E,Vashdi D,et al. Queues and fairness: A multiple study experimental investigation[R].(Technical Report) Technion-Israel Institute of Technology, 2005.

[10] Stanford D A. Waiting and interdeparture times in priority queues with poisson and general-arrival streams[J]. Operations Research,1995,45(5):725-735.

[11] Gavirneni S,Kulkarni V G. Self-selecting priority queues with burr distributed waiting costs[J].Production and Operations Management, 2016, 25(6): 979-992.

[12] Gavirneni S,Kulkarni V. Concierge medicine applying rational economicsto health care queuing[J].Cornell Hospitality Quarterly, 2014,55(3):314-325.

[13] Wang Jianfu, Baron O, Scheller-Wolf A. M/M/c queue with two priority classes[J].Operations Research, 2015, 63(3): 733-749.

[14] Yang Luyi., Debo L G, Gupta V. Trading time in a congested environment[J].Management Science, 2016, 63(7):2377-2395.

[15] Kleinrock L. Optimum bribing for queue position[J]. Operations Research,1967,15(2):304-318.

[17] Garton A, Daly J H. How do delay announcements shape customer behavior? An empirical study[J]. Management Science, 2016,6(4):195-200.

[18] Avi-Itzhak B,Levy H,Raz D. Quantifying fairness in queuing systems: Principles, approaches, and applicability[J]. Probability in the Engineeringand Information Sciences,2008,22(4):495-517.

[19] Raz D,Levy H,Avi-Itzhak B. Class prioritization and server dedication in queueing systems: Discrimination and fairness aspects[J]. Performance Evalution,2010,67(4):235-247.

[20] Sandmann W. Quantitative fairness for assessing perceived service quality in queues[J]. Operational Research, 2013,13(2):153-186.

[21] 阎崇军,唐加福,姜博文,等. 考虑患者选择和公平性的序列预约调度方法[J].系统工程学报,2014,29(1):105-112.

[22] Geng Xin,Huh W T,Nagarajan M. Fairness among servers when capacity decisions are endogenous[J]. Production and Operations Management, 2015,24(6):961-974.

[23] Larson R C. Perspectives on queues: Social justice and the psychology of queueing[J].Operations Research，1987，35(6)：895-905.

[24] Gross D,Harris C M. Fundamentals of queueing theory(Third Edition)[M]. New York：Wiley, 2008.