基于分布式光纤技术的古建木结构变形监测策略

吴铭昊,唐伟杰,姜绍飞,沈 圣

(福州大学土木工程学院,福建 福州 350116)

0 引言

古建筑倒塌失效具有突发性[1]和灾难性等特点,建立古建筑实时监测预警系统,对失效过程进行监控预防十分重要. 结构变形监控是监测中直接而有效的手段,分为宏观变形和微观变形(微应变对应裂缝观测)监控. 常见的宏观变形包括柱架倾斜变形、 梁坊挠度变形和脱榫[2]等. 我国规范[3]规定应对建筑物的宏观和微观变形进行定期观测.

国外较早开展对古建筑的监测工作[4-6]. 国内古建监测起步较晚,但也逐渐得到重视. 江南某宋代木构架[7]、 应县木塔[8]和宁波保国寺[9]均布设监测系统,为古建筑状态评价和预警提供科学参考. 虽然一些古建筑布设监测系统,但仍存在一些弊端. 由于每个传感器后端需要独立的数据线和控制器相连接,每种类型的传感器所配置的控制器类型也各有不同,这导致系统后端的通道线和终端控制器数量十分庞大,长期监测需要耗费较多人力来维护信号线畅通和系统正常运营.

基于分布式光纤技术的变形监测策略[10]可实现传感元件串联和通道共用,简化系统构成,可解决上述问题. 目前光纤技术仅应用于木结构应变监测[11-13],还未应用于木结构挠度和倾斜等宏观变形量监测. 而基于应变的桥梁和隧道挠度测量方法研究虽然已取得一定成果[10, 14],但古建木结构有其自身的特点,如： 榫卯半刚性支座条件,木梁跨高比较桥梁结构小,树木生长出现“根部较粗、 顶部较细截面不规则现象”,所以应用于桥梁隧道的挠度测量方法在古建木梁中是否适用还有待研究. 因此,研发适用于古建木结构的监测方法、 确定方法的适用性和仪器布设策略对保护传统建筑意义重大.

以共轭梁理论和空间几何关系为理论基础,在分析古建木结构变形机理的基础上推导梁柱应变分布和其宏观变形之间的关系. 通过仿真和理论分析探讨上述关系在古建木结构中的适用性,提出基于分布式光纤技术的古建木结构变形监测策略. 进行木梁静力和木柱推覆试验对所提策略的有效性进行验证. 由于篇幅有限,榫卯节点松动和结构沉降监测不在本研究讨论范围.

1 分布式光纤应变传感技术监测策略

采用光纤应变传感器(FBG)串联黏贴在待测梁柱表面监测应变. 基于间接方法将测得的应变换算得到梁柱宏观变形量,实现古建木结构的内力分布和梁柱宏观变形的监测.

1.1 基于分布式应变测量的木梁挠度变形监测方法

1.1.1 基于应变测量的古建木梁挠度计算方法

根据欧拉梁理论,简支纯弯梁梁体挠度ω(x)同应变Δε(x)和梁高Δz(x)的关系如下式所示：

(1)

古建木梁两端为榫卯半刚性连接[15], 不同于简支梁,当受到外部荷载和沉降时支座会产生弯矩引起梁体应变分布的改变,对式(1)挠度计算产生影响. 如图1所示,榫卯支座可等效为一简支梁叠加上端部附加弯矩M的形式,由于简支梁支座沉降并不引起梁体应变变化,因此带榫卯节点木梁总应变Δε分为简支梁由荷载F产生的应变ΔεF及半刚性支座等效附加弯矩M产生的应变ΔεM,如下式：

Δε(x)=ΔεF(x)+ΔεM(x)

(2)

式中：Δε为总应变；ΔεM为半刚性支座等效附加弯矩产生的应变；ΔεF为简支梁由荷载所产生的应变.

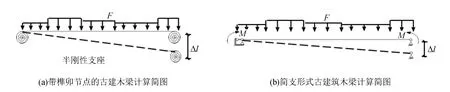
图1 古建木梁的计算简图Fig.1 Analytical diagram of ancient timber beam

从图1(b)可看出,梁体在等效弯矩作用下所附加的应变分布ΔεM仍满足式(1)的形式,假定ΔεF和ΔεM所对应的梁体挠度值分别为ΔωF和ΔωM,将ΔεF和ΔεM叠加并代入式(1)中进行积分：

(3)

可见,式(1)对于受到支座沉降和外部荷载作用下带榫卯节点的古建木梁挠度计算同样适用.

对简支梁而言支座沉降值ωv不引起梁体应变变化. 由于式(3)已考虑支座等效弯矩对梁体应变的影响,因此考虑支座沉降因素的古木梁挠度值ωs可按比例叠加左右端沉降值sl和sr在式(3)上：

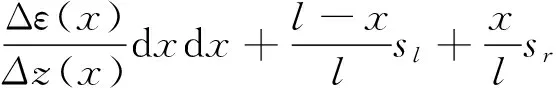
(4)

式中： sl和sr为左右两支座的沉降大小； l为梁长； x为测点与梁左边界的距离.

将式(1)单元化,通过共轭梁理论[16]结合式(1)和式(4)求得木梁挠度计算公式：

(5)

式中：ωp为p和p+1单元分界点处的挠度变形值；n为所要计算木梁单元的总个数；εi为木梁各单元上表面和下表面的平均应变差值；z为木梁截面高度； Δl为各单元长度.

式(5)中已包含了截面计算高度z,原木梁截面不规则已在算法中得到体现. 另外有以下两个因素影响算法精度： 1)跨高比,即剪切变形的影响； 2)单元划分数量,也即传感器数量.

1.1.2 挠度监测方法的适用范围探讨

将FBG按等间距布设于梁各单元表面测量该单元应变,配合其他测量方法得到梁端沉降值并由式(5)求得木梁挠度值. 取木梁跨高比k范围为20～40[17],取跨度范围3～7m的木梁进行划分单元数量的探讨[18]. 采用Ansys建立单跨透榫木框架仿真模型,对比不同跨高比和划分单元数量对计算的影响. 梁截面尺寸取高宽度比为3∶2[17]. 采用Solid45单元建模,榫卯节点采用Contan174和Target170建立接触对,摩擦系数取0.4[19],柱底铰接连接,模型材性参数见表1,计算结果误差如图2所示.

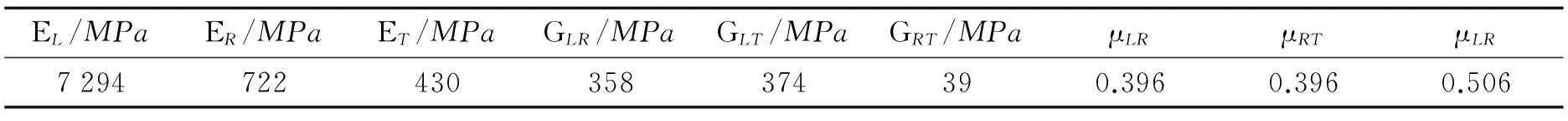
表1 福建杉木材性Tab.1 Material properties of Chinese fir in Fujian

注： 表中L, R, T代表顺纹,径向和弦向.

图2 不同跨高比的梁挠度计算结果Fig.2 Analytical result of timber beams under different span-depth ratios and spans

图2(a)为当l=7 m,跨高比k=20和划分单元数量n为6时的计算结果. 对k、n和梁长度l进行参数分析得到计算误差见图2(b)-(f). 可以看出： 1)k=20时,l<5 m的木梁需8～10个测点才能有较好的精度； 2)k=25时,l<5 m的木梁需6个测点其最大误差在3%左右,l>5 m的木梁需8～10个测点才能获得较好的精度； 3)k≥ 30时,所有木梁仅需6个测点其误差能控制在4%以内,且5 m以下的木梁误差全都在3%以内. 可见计算误差随测点n的增加而降低,k越大计算精度越好. 因此建议： 1) 跨高比k在30及以上的木梁,需布设6个测点； 2) 跨高比k在25～30之间的木梁,需布设8个测点； 3) 对于跨高比k介于20～25的木梁,跨度大于5 m时布设10个测点,跨度小于5 m时布设8个测点.

1.2 古建木柱倾斜变形监测方法

1.2.1 基于光纤应变的古建木柱倾斜变形方法

古建木结构中柱脚和柱础的连接做法为柱脚平搁放置于柱础石上,即如图3(a)所示的柱础分离式,本文假定推覆过程中柱架本身弯曲变形可以忽略,该假定将在第3节得到验证.

如图3(b)所示定义O点为柱底部圆心,O’点为柱础石圆心,当柱绕点D点转动时,倾角θ的数值大小为：

(6)

由于柱础和柱脚的缝隙通常非常小,缝隙距离lO无法通过放置仪器直接测量得到. 采用几何关系推导lO： 在柱础平面和柱脚平面建立空间四边形如图3(c)所示,容易求得Q3B的长度d1、Q2B长度d2和BO’长度d3,则AB长度lA可由P2Q2长度l2和P3Q3长度l3按等比关系求得：

(7)

观察图3(c)中的梯形ABQ1P1,则lO可由AB长度lAB和P1Q1长度l1按等比关系计算,如下式：

(8)

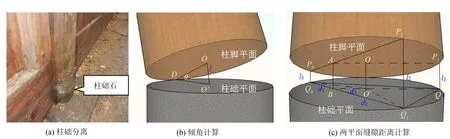
图3 古建木柱倾斜计算示意图Fig.3 Analytical sketch of angle

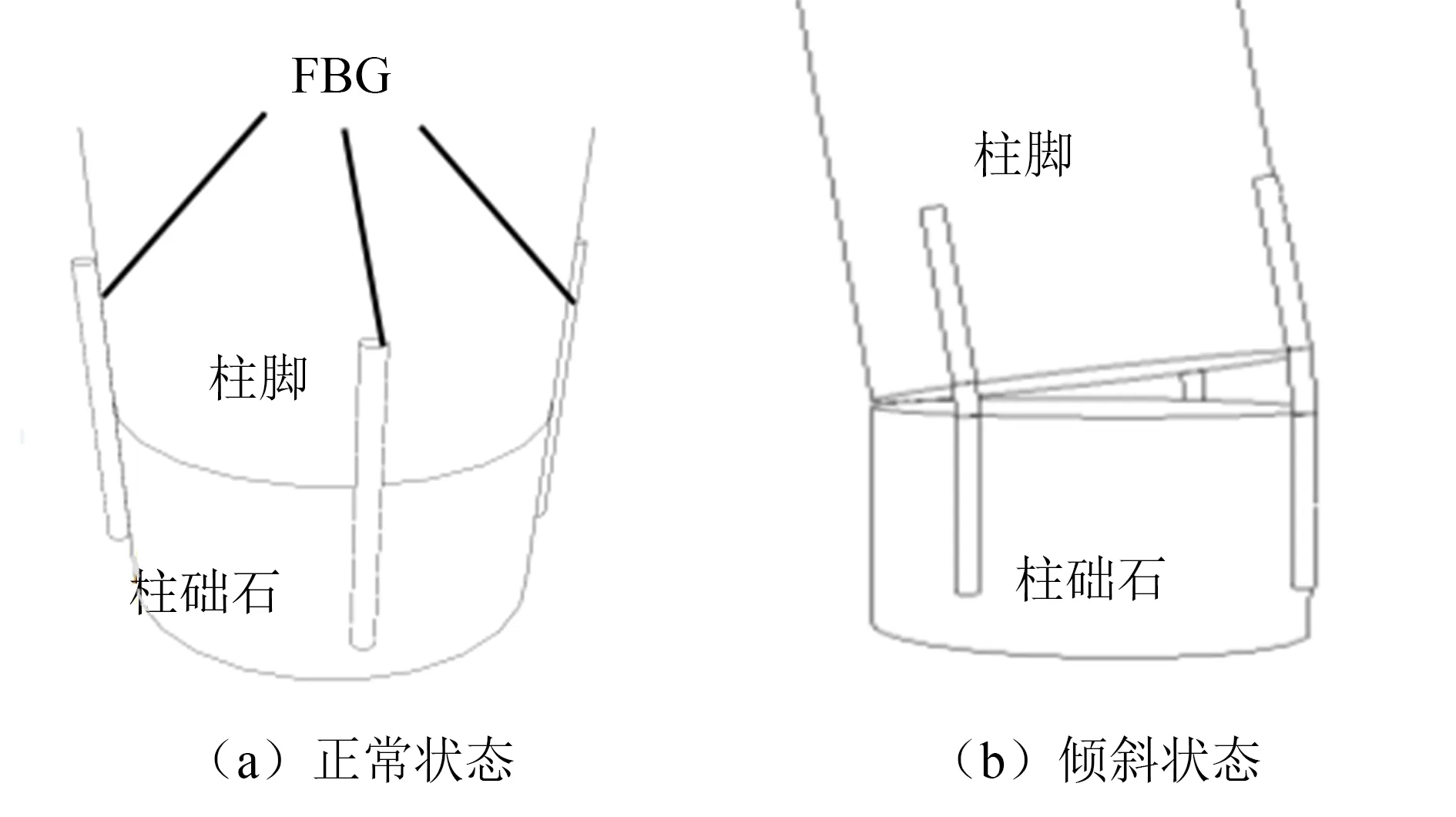
图4 传感器布设示意图Fig.4 Layout of sensors

将式(8)代入式(6)中即可得到倾角θ的数值大小. l1、 l2和l3可由结构外表面的仪器量得.

采用FBG应变传感器按图4所示来布设测量其数值大小. 在柱脚和柱础石边界上选取3个测点安装FBG. 当柱身倾斜时l1、 l2和l3可由FBG传感器所测得的应变ε和传感器标距λ乘积来求得.

1.2.2 特殊性和适用性探讨

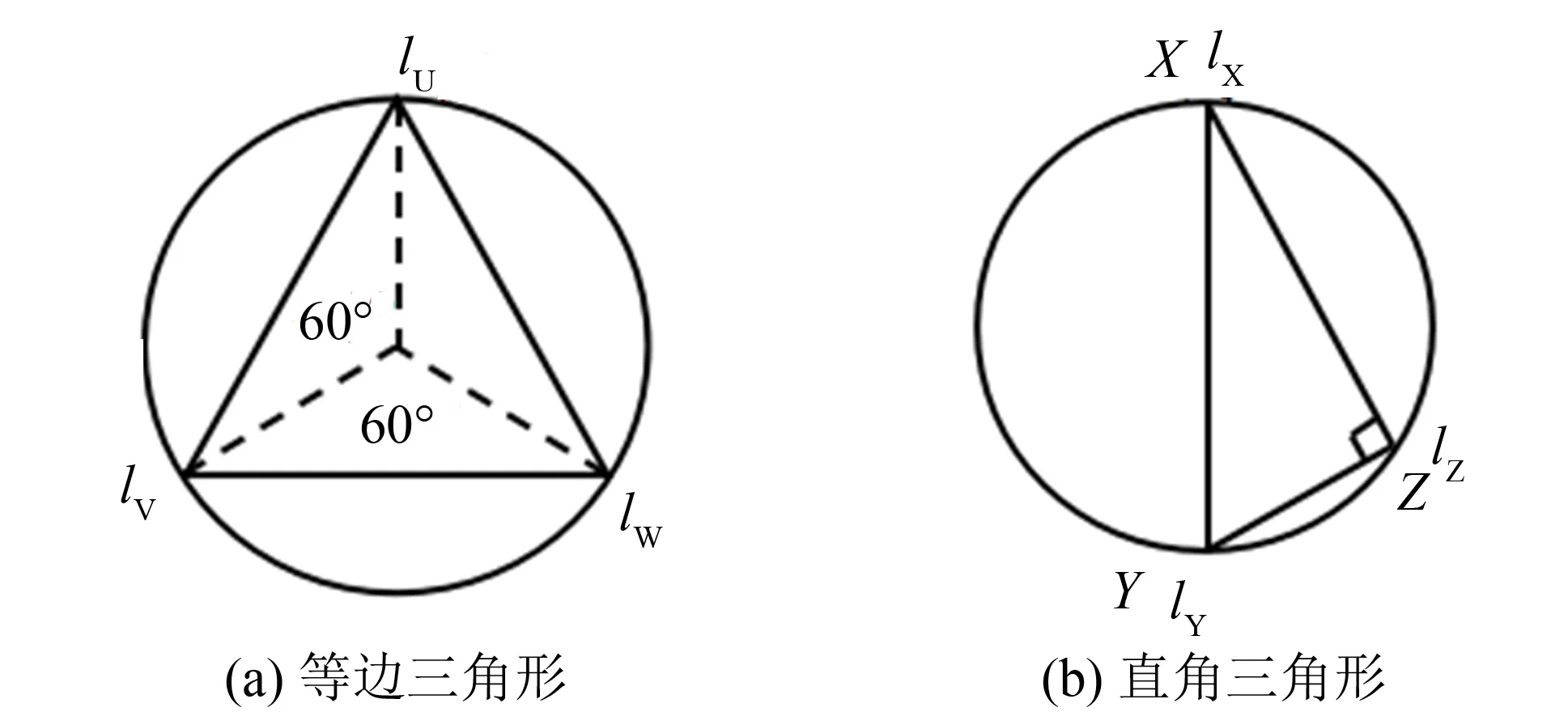
图5 测点特殊布设Fig.5 Layout of measure point for special condition

图5为二种较为特殊的布置方法,即3个测点呈等边和直角三角形, 假定lU、 lV和lW为图5(a)中等边三角形3个测点在倾斜前后的伸长量,lX、 lY和lZ为图5(b)中直角三角形3个测点X、 Y和Z在倾斜前后的伸长量. 则式(8)可变形为：

(9)

(10)

这样计算更为简便. 当3测点围成直角三角形时,若柱子倾斜方向与3测点与圆心的连线相平行,则该方向受拉传感器应变增长速率较其余工况快,造成其最先到达量程,在应用时应避免此方式. 古建木结构整体倾斜最大限值为θ>1/120[3],可知最大倾角限值为0.48°. 当3测点围成直角三角形且柱子倾斜方向和某测点与圆心连线平行时会使传感器产生最大拉应变,则式(10)可变形如下式：

(11)

将式(11)代入到式(6)可得到：

(12)

式中： λ为传感器标距； lm和εm为伸长量和应变,假定传感器所在测点与圆心连线与柱子倾斜方向一致.

由上式可知传感器标距λ越长,可测得倾斜范围也越大. 现有工艺允许FBG最大拉向微应变约为7 000 ,可求得传感器标距λ和待测柱子半径r之间对应关系如表2所示.

表2 不同标距对应的柱半径最大值

Tab.2 Maximum radius of column with different gauge length

(mm)

λ1002003004005006007008001000r42.0084.00125.33167.11208.89250.67292.45334.23417.78

可以看出正常柱径范围内所需要的传感器标距通常在100 mm以上,考虑FBG传感器的标距可以长达100～1 000 mm,因此完全可以胜任表2中正常柱径范围内的倾斜监测. 在实际监测中,当确定待测柱子的半径后,可根据表2选择合适的FBG传感器的标距λ来满足实际测量中的倾角测量要求.

2 木框架梁挠度变形监测方法试验验证

2.1 静力试验概述

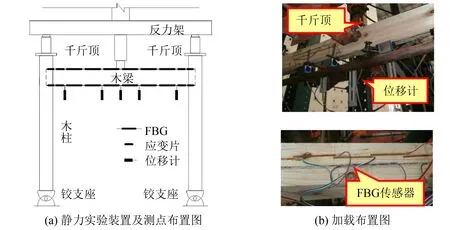
图6 试验装置和测点布置图Fig.6 Test setup and layout of sensors

为验证所提古建木结构梁坊扰度变形监测策略的有效性,选用殿堂二等材[18]按缩尺比例1∶3.52制作透榫木框架模型,如图6所示,梁长l=2.4 m,柱高H=1.8 m,梁高z为120 mm. 梁跨中和两侧柱头采用千斤顶加载10 kN模拟上部屋面荷载. 木梁共均分8个单元,每个单元长300 mm. 在各单元上下表面中部将FBG传感器锚固端两侧粘贴固定于木梁表面,在梁底跨中和边支座位置安装位移计来测量梁体的挠度变形值. 试验过程中各单元边界点各级挠度值通过FBG测得的应变数值代入式(5)中得到.

2.2 试验过程及结果分析

表3列出了各级荷载作用下木梁两端支座测得的沉降值,各单元FBG传感器在跨中荷载F作用下的上下表面测得的应变差值ε绝对值如表4示. 以跨中挠度值为例来说明计算过程,梁高z=120 mm,梁长l=2 400 mm,跨中处单元下标i=4,则式(5)中可变形如下式：

(13)表3 各级荷载作用下框架梁端沉降值Tab.3 Settlement values at beam ends of timber frame model under different load levels

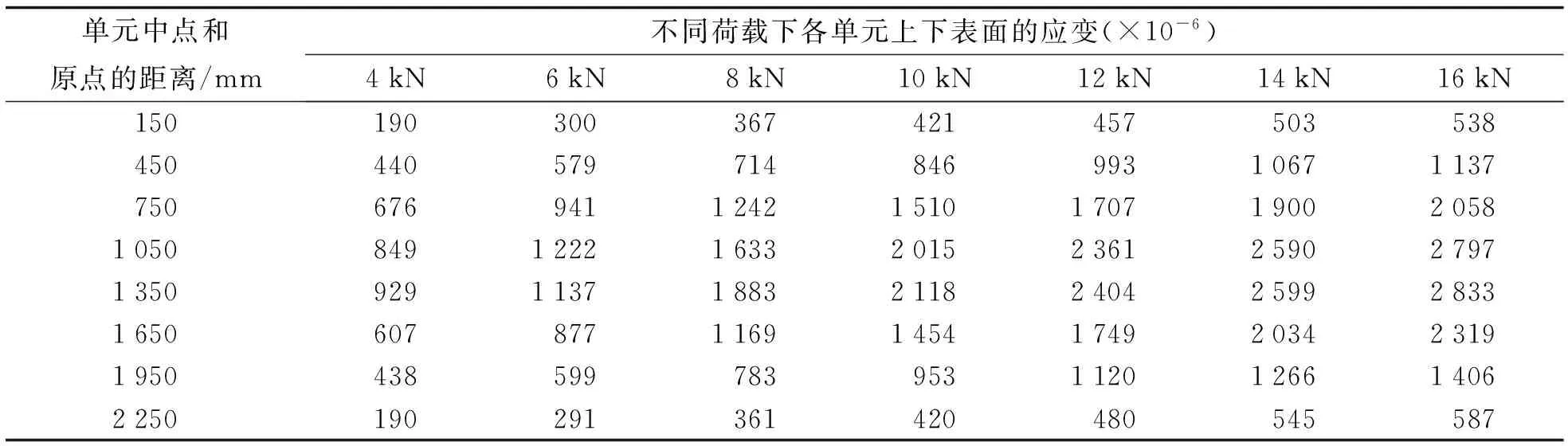
表4 各单元上下表面平均应变差值Tab.4 Difference of strain of each element on the upper and lower surface

图7为通过式(3)计算得到的静力试验结果. CV代表通过应变计算得到的挠度值,MV表示位移计实测得到的挠度值. 可以看出加载初期误差较大,随着加载级数的增加CV与MV趋于一致,当跨中挠度为13 mm时误差为5.7%,说明该监测方法具有较高精度. 分析误差原因为： 欧拉梁理论未考虑剪切变形对应变的影响,而梁跨高比越大则剪切变形的影响也越小,该算法精度也越高. 本文所设计的梁跨高比k约为20,目前大多在役古建承重木梁跨高比k范围约在20～40之间[18],可见该方法能够适用于现役古建木梁的挠度变形监测.

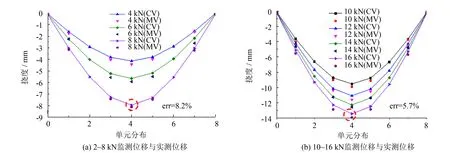
图7 静力试验结果Fig.7 Result of statistic load test

3 木柱倾斜变形监测方法试验验证

3.1 试验概述

为验证所提古建木结构柱倾斜变形监测方法的有效性,制作单柱模型进行推覆试验, 如图8所示,柱直径200 mm,柱高2 000 mm. 通过6根带弹簧钢丝绳施加柱顶轴力来保持柱身稳定,每根钢丝绳连接力传感器以查看钢丝绳张拉力大小,加载前预先对6根钢丝绳扭动弹簧施加预紧力来模拟柱顶轴力并稳定柱身. 施加预紧力后,将3个标距为300 mm的FBG传感器按等边三角形粘贴在柱础石和柱脚连接处.

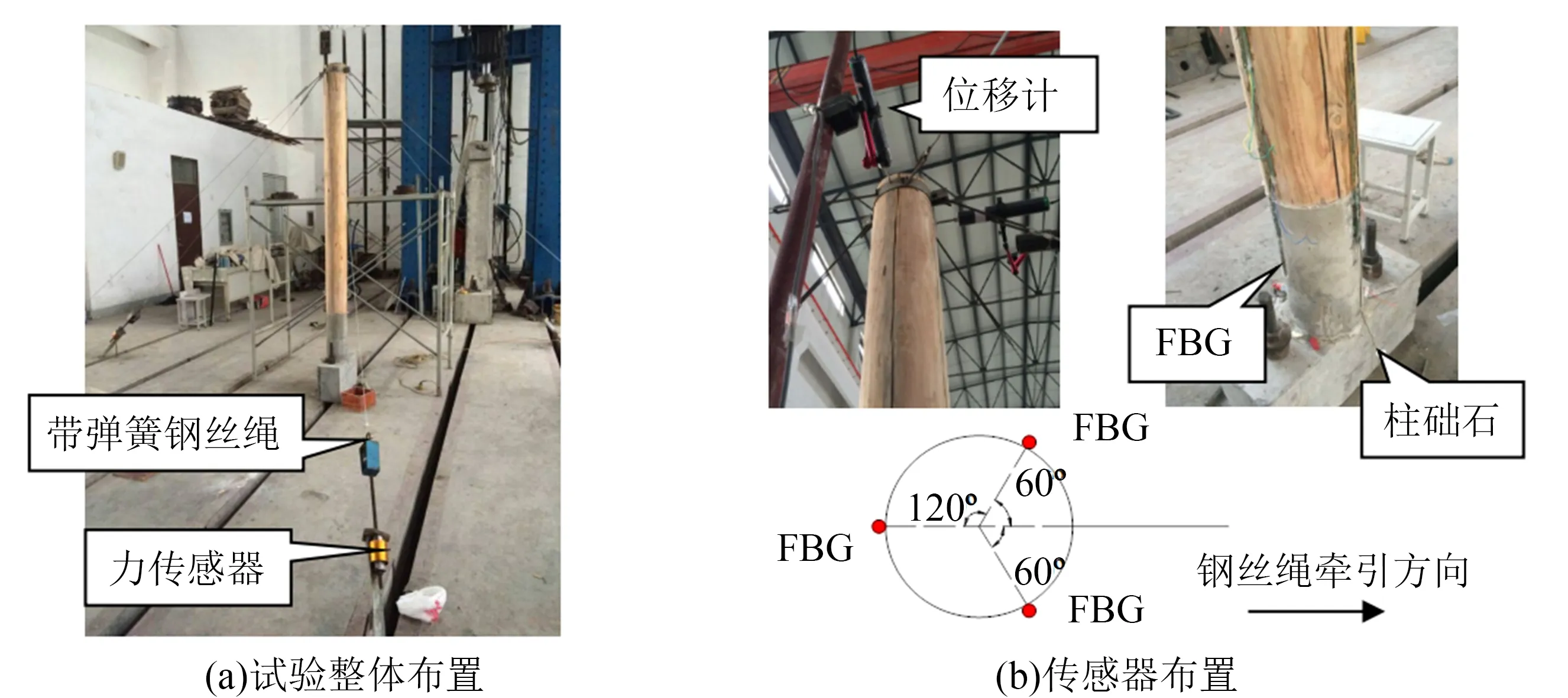
图8 倾斜试验装置图Fig.8 Test setup of tilt test

加载时在需倾斜方向牵引一根钢丝绳让柱子缓慢倾斜,为保护传感器当拉应变接近6×10-3时停止试验. 沿柱身两侧隔40 cm黏贴应变片分析柱身变形. 在柱头和柱中表面沿倾斜的平行和垂直方向各安装一个位移计来测量水平位移,将两方向水平位移加权平均再除以柱身长度得到柱身倾斜角度.

3.2 倾斜试验过程和结果分析

试验分加载和卸载阶段,以FBG传感器拉应变幅值约5×10-4为一级,为保护传感器当拉应变达到6×10-3时即进入卸载阶段. 表5和表6给出了试验阶段FBG所测得的应变大小. 3个传感器同圆心连线呈120°,将表5～6中的应变值代入式(9)求得lO,再代入式(6)可求得倾角θ, 见图9.

表5 加载时FBG传感器应变数值Tab.5 Strain values of FBG sensors at the stage of loading

表6 卸载时FBG传感器应变数值Tab.6 Strain values of FBG sensors at the stage of unloading

图9(a)和9(b)为试验倾角曲线和计算误差. 可看出位移计在柱头和柱中所测得的倾角基本一致,说明柱子主要呈刚体转动. 试验整体误差在5%左右,说明该方法具有较好的精度. 误差原因是因本次试验为小变形测量,位移计在测量小变形的情况下存在误差. 另外当FBG处于其极限应变前(6×10-3)柱子倾斜量程已达到残损限值0.48°,说明该监测方法能够满足实际工程中测量需求.

图10为应变片测得的柱身应变值. 可看出最大应变不超过正负4×10-5,柱子本身变形很小,这与文献[19]的研究结果相一致. 表7为文献[20]中一木框架推覆过程中柱头水平位移为180 mm时的柱身挠曲变形,可以看出柱身挠曲变形只为柱头水平侧移的1/1 000,木框架在倾斜过程中柱接近于刚体转动.

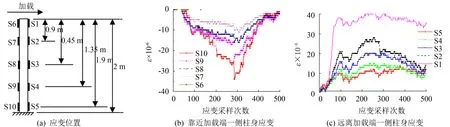
图10 柱身应变数数值Fig.10 Strain values on the column表7 木构架柱子挠曲位移Tab.7 Flexure deformation of timbercolumn

(mm)

注： 测点1～7表示文献[20]中木框架柱身上挠曲变形的测点编号,一共布置了7个测点来全面反映柱身的挠曲变形.

4 结语

1) 仿真和理论分析表明,基于分布式光纤技术的古建木梁变形监测方法适用于跨高比大于20以上的木梁. 对于5 m以下的木梁需6个传感器可满足精度要求,对于大于5 m的古建木梁需8个及以上的传感器才能满足精度需求. 在实际布设时建议将3个测点围成等腰、 等边或直角三角形进行布设,传感器的标距长度可根据待测柱子的直径并参照表2进行选取.

2) 试验结果表明,所提变形监测方法具有较高精度,梁挠度变形监测最大误差为8.2%,柱子倾斜变形监测最大误差为8%,且可以满足实际工程监测中最大测量范围的要求.

3) 基于分布式光纤应变技术的古建木结构变形监测策略实现了采用单一传感器监测古建梁坊挠度、 柱倾斜和结构应变3种变形量,简化了系统构成,具有良好的工程应用前景.

虽然通过仿真和理论分析得到的传感器布设建议和适用范围能够对实际工程应用起到一定的借鉴作用,但其在实际工程中的精度还需要现场测试得到进一步的验证,而这也是本研究的不足之处. 后续研究将在实际工程上布设监测系统来验证所提方法的适用性.

[1] 姚侃, 赵鸿铁, 薛建阳, 等. 古建筑木构架的整体稳定性分析[J]. 世界地震工程, 2008, 24(1): 73-76.

[2] 陈国莹. 古建筑旧木材材质变化及影响建筑形变的研究[J]. 古建园林技术, 2003 (3): 49-60.

[3] 四川省建筑科学研究院. 古建筑木结构维护与加固技术规范: GB 50165-1992 [S]. 北京： 中国建筑工业出版社,1993.

[4] LORENZONI F, CASARIN F, MODENA C,etal. Structural health monitoring of the Roman Arena of Verona, Italy[J]. Journal of Civil Structural Health Monitoring, 2013, 3(4): 227-246.

[5] MIN K W, KIM J, PARK S A,etal. Ambient vibration testing for story stiffness estimation of a heritage timber building[J]. Scientific World Journal, 2013, 2013: 206-232.

[6] HU L, DOUDAK G, SMITH I,etal. Monitoring structural response of a wooden light-frame industrial shed building to environmental loads[J]. Journal of Structural Engineering, 2005, 131(5): 794-805.

[7] 路杨, 吕冰, 王剑斐. 木构文物建筑保护监测系统的设计与实施[J]. 河南大学学报(自然科学版), 2009, 39(3): 327-330.

[8]王林安,候卫东,永昕泉. 应县木塔结构监测与试验分析研究综述[J]. 中国文物科学研究,2012(3)： 62-67.

[9]余如龙. 构建科技监测体系, 加强文物建筑科学保护力度： 浅析浙江宁波保国寺大殿科技保护项目及应用[C]// 建筑历史与理论(第九辑).开封： 中国建筑学会建筑史学分会, 2008： 413-417.

[10] SHEN S, WU Z S, YANG C Q,etal. An improved conjugated beam method for deformation monitoring with a distribution sensitive fiber optical sensors [J]. Structure Health Monitoring, 2010, 9(4): 361-378.

[11] 任小芳, 贾栋, 赵辉, 等,基于光纤Bragg光栅的古建筑结构健康监测技术研究[J]. 传感技术学报, 2015, 28(1): 34-38.

[12] 王娟,杨娜,杨庆山,适用于遗产建筑的结构健康监测系统[J]. 北京交通大学学报,2010, 34(1): 100-104.

[13] DAI L, YANG N, ZHANG L,etal. Monitoring crowd load effect on typical ancient Tibetan building[J]. Structural Control and Health Monitoring, 2016, 23(7): 998-1014.

[14] 宋彦君, 刘寒冰, 谭国金,等. 基于应变计的梁式桥位移响应测试方法[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 198-201.

[15] 周乾, 闫维明, 周宏宇, 等. 钢构件加固古建筑榫卯节点抗震试验[J]. 应用基础与工程科学学报, 2012, 20(6): 1063-1071.

[16] 沈圣, 吴智深, 杨才千, 等. 基于分布式光纤应变传感技术的改进共轭梁法监测结构变形分布研究[J]. 土木工程学报, 2010, 43(7): 63-70.

[17] 梁思成. 营造法式注释[M]. 北京： 中国建筑工业出版社, 1983.

[18] 王天. 古代大木作静力初探[M]． 北京： 文物出版社,1992.

[19] 赵鸿铁, 张锡成, 薛建阳, 等. 中国木结构古建筑的概念设计思想[J]. 西安建筑科技大学学报(自然科学版), 2011, 43(4): 457-463.

[20] 林冬勇. 木结构变形监测与节点损伤识别研究[D]. 福州: 福州大学, 2014.