采用二阶Keystone变换的机动目标ISAR成像算法

杨 旭 皮亦鸣 李 晋 刘 通

(电子科技大学信息与通信工程学院，四川成都 611731)

1 引言

基于传统的距离多普勒成像原理的逆合成孔径雷达(Inverse Synthetic Aperture Radar，ISAR)能获取运动目标的高分辨雷达图像，进而被广泛地运用到运动目标的自动识别和分类[1]。通常情况下，ISAR成像的第一步是运动补偿，由距离对齐(平移与旋转引起的距离徙动校正)和相位校正两步构成。然后，目标在成像时间内做匀速旋转的条件下，传统的距离多普勒算法可获得清晰且聚焦的ISAR图像[2- 4]。然而，真实世界中的待成像目标(飞机和舰船等)在机动时通常具有复杂的运动分量(如：速度，加速度以及加速度速率等)[5- 6]。这些运动分量造成距离弯曲和多普勒频移的非线性，从而导致传统的距离多普勒成像算法对机动目标失效。

对具有复杂运动的机动目标进行ISAR成像，目前的解决方法大致分为时频分析方法[7-9]、相关算法[3- 4,10]和非相关算法三类[6,11-13]。时频分析方法假设目标在短时间内做匀速运动，然而，较短的积累时间导致方位向分辨率降低。相关算法存在交叉项干扰并且要求较高的信噪比。非相关算法尽管可以在低信噪比条件下获得高的抗噪声性能，但是较高的计算负荷而不适用于真实的成像场景。相关算法和非相关算法将目标回波近似为线性调频信号，然后通过参数搜索与估计的方法提取点目标位置，然而这些方法仅对具有有限个点目标的成像有效，对于面目标或者高分辨率成像雷达，这类算法将失效或者计算量大大增加。

Keystone变换是一种流行的运动补偿算法，该方法可消除任意的线性距离徙动而不需知道目标的运动参数[14]。针对具有复杂运动的机动目标在相干成像时间内产生的一阶距离徙动和二阶距离徙动的问题，本文提出了基于二阶Keystone变换的二维ISAR成像算法。文章首先结合去调频接收机技术，建立并分析了机动目标的回波信号模型，并对回波信号使用二阶Keystone变换以去除二阶距离徙动。然后，采用FrFT估计二阶Keystone变换后新生成的二次相位项的调频斜率，利用估计的调频斜率补偿新生成的二次相位项。对补偿后的回波信号再一次使用二阶Keystone变换去除一阶距离徙动。最后，对回波信号使用2D FFT获取机动目标的高分辨2D ISAR图像。数值仿真和实测数据表明，本文所提方法成像性能优于直接的距离多普勒算法。

2 信号模型

机动目标的ISAR成像几何如图1所示。雷达位于笛卡尔直角坐标系统(U,V)的原点，目标的几何中心视为直角坐标系(x,y)的原点。为描述目标的旋转运动，另构建一个参考坐标系统(X,Y)，该参考坐标系是雷达坐标系统的平移版本，且与目标坐标系统共原点o。 假设目标上的第i个点目标的坐标为p(xi,yi)，则点目标p与雷达的瞬时斜距可以表示为[8]：

RiP=[(TX+xicosθ-yisinθ)2+(TY+xisinθ+yicosθ)2]1/2=

R0+xicos(θ-α)-yisin(θ-α)

(1)

公式(1)中，R0为目标参考点，即点o与雷达的初始距离，θ为相对于参考坐标系的初始旋转角度，α为目标相对于雷达坐标系的方位角，TX与TY为参考坐标系(X,Y)相对与雷达坐标系(U,V)的平移量。

图1 机动目标ISAR成像几何Fig.1 ISAR imaging geometry of maneuvering targets

机动目标相对于雷达的运动可分解为平移运动和旋转运动。 旋转运动分量和平移运动分量可表示为：

(2)

(3)

公式(2) 中，Ω为目标旋转速度，β为目标角加速度。 公式(3) 中，Vr为目标的平移速度，a为目标平移加速度。 因此，机动目标与雷达的瞬时距离可以描述为：

RP(tm)=R(tm)+xicos [θ(tm)-α]-yisin [θ(tm)-α]

(4)

不失一般性，目标相对与雷达坐标系的初始方位向角度α的值设为π/2，即Y轴作为距离轴，则公式(4)可简化为：

RP(tm)=R(tm) +xisin [θ(tm)] +yicos [θ(tm)]

(5)

通常情况下，目标相对于雷达的旋转角度较小 (一般为3°～5°)，因此，sin[θ(tm)]≈Ωtm和cos[θ(tm)]≈1。将公式(2)和(3)代入公式(5)可得：

(6)

2.1 雷达信号回波模型

为兼顾发射功率和发射信号大带宽的要求，线性调频信号被广泛地运用于雷达与通信等领域。 假设雷达发射的信号为脉冲线性调频信号，则信号模型可描述为：

(7)

sR(t)=

式中，σp为点目标p的散射强度，τ=2Rp(tm)/c为回波双程时延，c为电磁波在真空中的传输速度。 为了降低对A/D转换器件采样速率的要求，去调频技术被广泛地运用到线性调频雷达中。 去调频后的基带信号可以表示为：

(9)

式中，Rs为参考距离。式 (9) 中的第二个指数项为去调频技术特有的剩余视频相位项 (RVP)，会引起多普勒发生变化，需要对进行补偿[15]。RVP被完全补偿之后，公式 (9) 被简化为：

(10)

为了简化符号描述，做以下的变量替换：

(11)

Kr)(R0-Rs+yi)]×exp{-j 2(Kc+

(12)

式中，BWk=2πTr/c为发射信号的波数域宽度。表1给出了公式 (12)中各相位项对成像的影响。对波数变量Kr做傅里叶反变换即可获得目标的距离维，该距离维是一个关于横向距离、角速度、径向加速度和慢时间的函数，即是一个瞬时函数。距离的漂移可以描述为：

(13)

式(13)表明：当距离漂移Δr大于距离分辨率时，会导致生成的图像模糊。因此，瞬时距离波数Kr与慢时间tm之间的耦合需要去除。

表1 相位项描述

2.2 ISAR成像算法

Keystone变换被广泛地运用到动目标的距离徙动校正，该方法的优势是不需要知道目标的运动参数[3-5]。为了去除式 (12) 中二次相位项造成的距离弯曲，对式 (12) 运用二阶Keystone变换以去除距离波数Kr与慢时间tm的耦合。二阶Keystone变换的公式为：

(14)

式中，um1为尺度变换后的时间。二阶Keystone变换之后，式 (12) 变成：

(15)

式中，η=aKc。从式(15)可以看出，与Kr相关的二次项已经被去除，但同时生成了与Kc相关的二次相位项，该二次项会导致图像在方位向上散焦，所以必须去除。

式(15)表明，对于一个给定的距离单元，方位向的相位是一个线性调频信号，该相位项为：

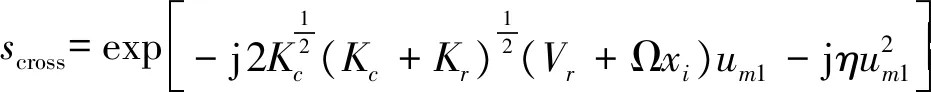
(16)

分数阶傅里叶变换 (FrFT) 被广泛地运用到线性调频信号的检测与估计[18]。 如图2所示，分数阶傅里叶变换是传统傅里叶变换的推广，可看成时频面上关于原点逆时针的旋转。

图2 chirp信号的时频分布及投影到傅里叶与分数阶傅里叶域Fig.2 Time-frequency distribution of a chirp signal and its projection onto Fourier and fractional Fourier domain

FrFT是一个一维线性变换，信号x(t)的FrFT可以描述为：

(17)

式中，q为FrFT的阶数，ρ=qπ/2，Fq{·}为FrFT运算符，Kρ(t,u)为FrFT的核，该核函数可表示为：

Kρ(t,u)=

(18)

该核函数具有以下性质：

(19)

因此，逆FrFT可以表示为：

(20)

式(20)表明信号x(t)为u域上chirp基函数的线性组合。如一个单分量chirp信号如式(21)所示：

x(t)=A0exp(jφ0+j 2πfc+πμt2),

-Δt/2≤t≤Δ/2

(21)

式中，A0、φ0、fc和μ为待估计的参数。由FrFT的定义可以看出，若chirp信号的时频分布以一个合适的角度ρ投影到旋转轴u上，则chirp信号的能量分布以最大幅度集中在一个最窄的区间。该性质可以被用来估计chirp信号的参数，通过在分布平面上搜索具有阈值的峰值实现参数估计。以公式(21)为例，相应的估计方法可以表示为：

(22)

(23)

为提升计算效率与精度，采用Ozaktals等人提出的处理算法[19]。

式(15)中的二次相位项被完全补偿完之后，式(15)变成

(24)

从式(24)可以看出瞬时距离波数Kr与慢时间um1存在耦合，为了去除该耦合，对式 (24)采用二阶Keystone变换。该二阶Keystone变换如式(25)所示。

(25)

二阶Keystone变换后的信号表示为：

Rs+yi)]×exp[-j 2Kr(R0-Rs+yi)]

exp[-j 2KcΩxium2]exp[-j 2KcVrum2]

(26)

式(26)中的第一个指数项是一个常数项，对ISAR成像没有影响，因此，该相位项可以忽略。第二个指数项与瞬时距离波数相关，对应的是目标的距离信息。第三项为目标的方位信息。第四项是目标在方位向上的整体平移，该相位项不会影响成像结果，可以通过质心估计去除。质心去除之后的信号变为：

Rs+yi)]exp[-j 2KcΩxium2]

(27)

式中，at=σpexp[-j 2Kc(R0-Rs+yi)]。

假设复杂目标由N个理想的点散射体构成，则接收到的回波信号可以表示为：

Rs+yi)]exp[-j 2KcΩxium2]

(28)

对式(28)做二维逆傅里叶变换可以获得目标的ISAR图像，ISAR图像的公式可以表述为：

(29)

式中，sinc=sin(πx)/(πx)，BWkx与BWky分别为方位和距离上的空间频率宽度，BWfx与BWfy分别为方位和距离上的时间频率宽度。本文提出的ISAR成像算法流程图如图3所示。

由图3所示，该成像算法需要进行两次Keystone变换、一次分数阶傅里叶变换，一次多普勒质心估计和一次二维逆傅里叶变换。由于Keystone变换可以通过CZT实现，而CZT变换的算法复杂度与快速傅里叶变换的算法复杂度一致。同时，分数阶傅里叶变换也可以通过快速傅里叶变换实现。此外，二维逆傅里叶变换的计算复杂度为一维快速傅里叶变换的两倍。假设成像所需的脉冲数量用Np表示，每个脉冲的距离单元数量为Nr，分数阶傅里叶变换的搜索角度数量用Na表示。因为一次Keystone变换的计算复杂度可以表示为O(NrNplog2Np)，所以两次Keystone变换的计算复杂度为O(2NrNplog2Np)。由于分数阶傅里叶变换可通过快速傅里叶变换实现，对每一个给定的搜索角，其计算复杂度为O(Nplog2Np)，则Na个搜索角的计算复杂度为O(NaNplog2Np)，二维逆傅里叶变换的计算复杂度为O(2NrNplog2Np)。因此本算法的计算复杂度为成像算法中所有计算步骤的算法复杂度之和，其计算复杂度大致为O(4NrNplog2Np+NaNplog2Np)。

图3 ISAR成像算法的流程图Fig.3 Flowchart of the proposed ISAR imaging algorithm

3 仿真与实测结果

为验证本文所提算法的有效性，本节分别通过数值仿真实验与实测数据进行验证。此外，为了验证本文所提算法的成像性能，与基于传统的二维FFT算法[20]的成像结果进行了对比实验分析。

3.1 仿真分析

图4 仿真目标及两种算法的成像结果Fig.4 Simulated point targets and imaging results using the direct 2D FFT and the proposed method

3.2 实测数据验证

为了验证本文所提方法对真实目标的成像能力，我们采用一套340 GHz的成像雷达系进行试验并成像。该系统采用脉冲线性调频机制[21-23]，工作带宽为28.8 GHz，采样频率为1.5625 MHz，雷达的脉冲重复频率为1 kHz，脉冲调频时间为300 ms，方位脉冲数目为1700。为了模仿真实的机动目标，本实验将两个边长为3 cm的角反射器放置于塑料泡沫之上，然后沿直线方向手动拖拽塑料泡沫。成像实验场景和目标如图5(a)所示。图5(b)为距离压缩后的成像结果，从图中可以看出随着慢时间的积累出现了距离徙动，该距离徙动由一阶距离走动和二阶距离弯曲组成，最后一个脉冲相对于第一个脉冲距离徙动单元数为21。图5(c)为第一次二阶Keystone后的成像结果，该结果表明距离弯曲被去除，剩余的距离走动量为12个距离单元。图5(d)为采用FrFT估计chirp信号调频斜率的结果，估计的chirp斜率为9.25。图5(e)为利用估计的chirp斜率去除新生成的二次相位项的结果。图5( f )为第二次采用二阶Keystone变换后的结果，从该图可以看出距离走动几乎完全被去除了。为了比较采用2D FFT和本文方法成像的性能，图5(g)给出了直接的2D FFT的成像结果，从该图可以明显看到慢时间与距离波数耦合造成的距离弯曲和距离走动，导致距离和方位的散焦。图5(h)为本论文提出的成像方法所得结果，可以看到两个角反射器的成像结果聚焦良好。

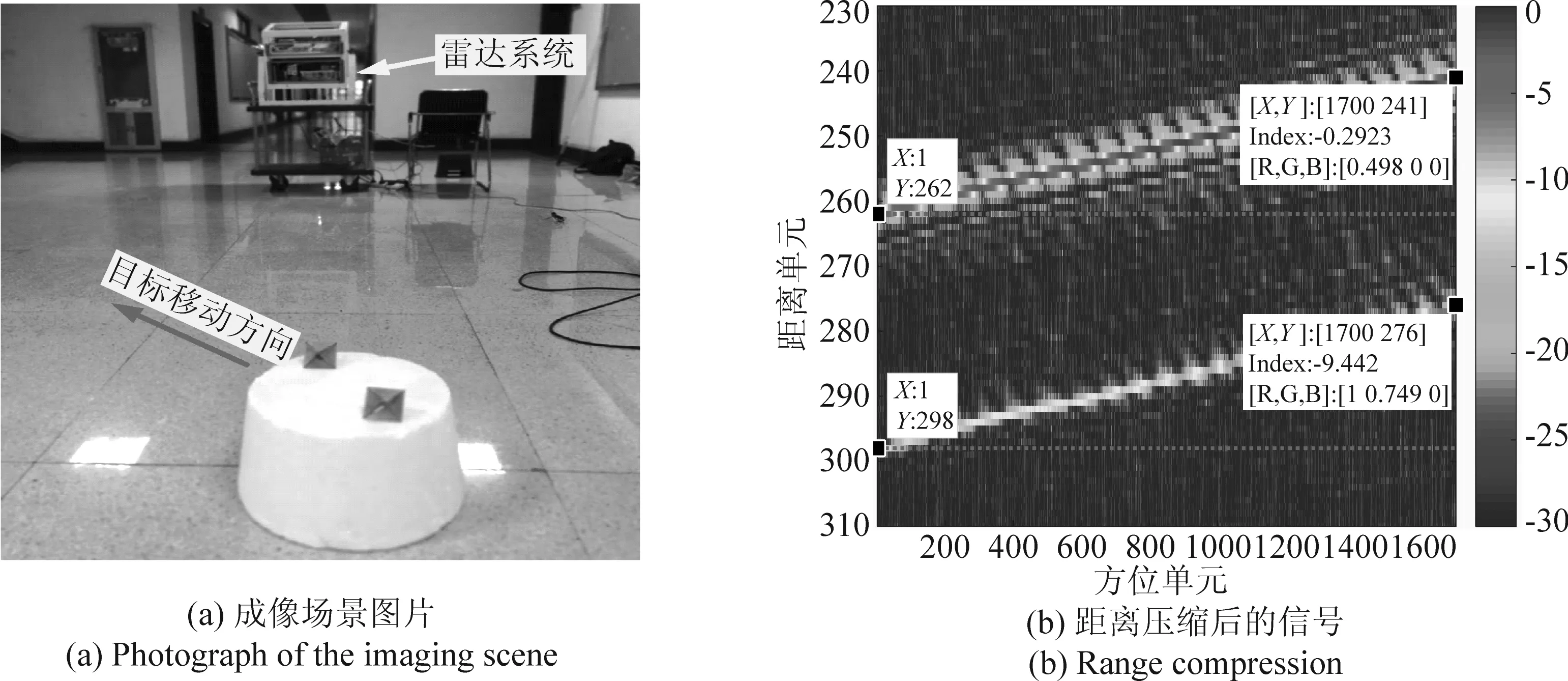
图5 实测数据成像结果Fig.5 Simulated point targets and imaging results using the direct 2D FFT and the proposed method

4 结论

本文提出了一种基于二阶Keystone变换的方法用于机动目标的ISAR成像。首先通过二阶Keystone变换对目标回波进行二次弯曲校正，但在校正二次弯曲的过程中产生新的二次相位项。该二次项与目标的加速度和雷达的载波频率有关，因此在每一个距离单元里是一个线性调频信号，本文采用FrFT估计该调频斜率，利用估计的线性调频斜率去除新生成的二次相位项。对去除二次相位项后的回波信号再一次采用二阶Keystone变换去除距离走动。最后通过2D FFT获取目标的二维ISAR图像。数值仿真实验和实测数据验证了本方法的有效性。该方法可以广泛地运用到具有低机动性的目标2D ISAR成像。