不同时长最大降雨量与河流最大洪峰流量关系研究
马惠群,王 勇
(山东电力工程咨询院有限公司,山东 济南 250013)
0 引 言
水利、电力工程设计应考虑防洪设计[1],推求设计洪水时须应让历史洪水参与其中,而历史洪水的获得一般需进行历史洪水调查,确定各次大洪水发生的时间及相应的重现期、洪水过程以及发生洪水时的雨情、水情和灾情等。在平原地区,历史洪水加成法是一种重要的设计洪水计算方法[2]。河道中的洪水由降雨引起,历史洪水加成法是采用历史最大洪水加上设计标准下的降雨量与当次洪水降雨量差值引起的流量变化值作为设计洪水的一种方法。但由于历史久远,被调查人员常常对于几日降雨引起洪峰流量模糊不清,而不同时长的降雨历时降雨量差别较大,从而引起计算洪峰流量加成差值较大,此时该如何选择降雨时长?本文采用水文分析中常用的Copula方法对此进行研究,以期为降雨和洪峰流量关系研究提供有效的途径。
1 Copula函数
Sklar[3]认为一个联合分布可以分解为k个边缘分布和一个Copula函数,这个Copula函数描述了变量间的相关性,它是把多个随机变量u1,u2,…,un的联合分布函数F(u1,u2,…,un)与各自的边缘分布函数Fu1(x1),Fu2(x2),…,Fun(xn)相联结,即联结函数C(u1,u2,…,un)使得
F(u1,u2,…,un)=C(Fu1(x1),Fu2(x2),…,Fun(xn))
(1)
等式成立。多元函数C(u1,u2,…,un)是存在的,它就是Copula函数,将多维分布与一维边缘分布联结在一起的函数。
2 Gumbel-Hougaard Copula函数
二维Gumbel-Hougaard Copula函数形式[4]如下:
C(u,v)=exp(-((-lnu)θ+(-lnv)θ)1/θ)
θ∈[1,+]
(2)
式中,φ(t)=(-lnt)θ,τ=1-θ-1。
若给定Y=y情况下,X的条件分布函数如下:
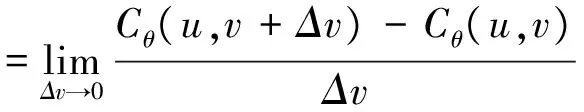
(3)
3 计算实例
小清河流域发源于济南诸泉群,南依泰山山脉,北界黄河,处于鲁中山区与华北平原的过渡地带,地形南高北低,自西南向东北倾斜,由南至北依次为山区、丘陵、平原、洼地。选用小清河黄台桥站的资料进行计算,黄台桥水文站[5]位于济南市二环东路小清河桥下游,建于1916年,是国家重点水文站,该站控制流域面积321 km2,主要观测项目有流量、水位、泥沙含量、水质等指标。现为自动观测设备,河道流量~水位关系稳定,冲淤基本平衡。为研究小清河降雨和洪峰流量关系,本研究共收集到其23年最大1日降雨量、最大15日降雨量和最大洪峰流量资料,统计特征值见表1。
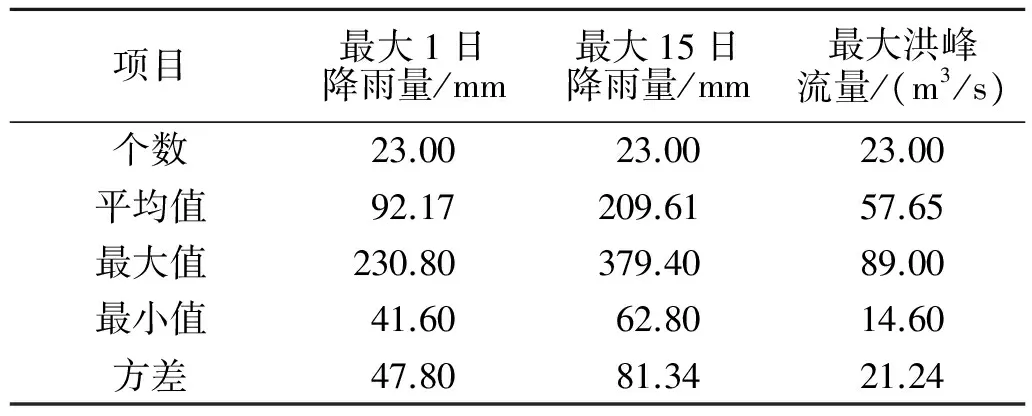
表1 不同变量统计特征值
三个变量之间的散点分布见图1。
边缘分布在正态分布、对数正态分布[6]、指数分布、威布尔分布[7]、最大极值分布、最小极值分布以及伽马分布中选取,以采用Gringorten position-plotting 公式计算经验频率[8,9],并以此作为基础计算均方误,其公式为:
(4)
式中,K表示数据序列升序排序序号;N表示样本总个数。
本研究采用均方误作为边缘分布拟合优劣的判断标准,均方误越小,说明采用此种边缘分布拟合越好。均方误采用下式进行计算:

图1 三个变量间相关图

(5)
式中,RMSE为均方误,也就是误方差的平方根;E为期望值,也就是平均值;N为样本总个数,在本研究中为23;Xc为不同频率分布公式的计算值;X0为观测值,在本文中以经验频率值表示观测值。均方误的计算结果见表2。

表2 均方误值
由表2可知,最大1日降雨量对数正态拟合最好,最大15日降雨量和最大洪峰流量正态分布拟合最好,边缘分布见图2。采用对数正态分布求得,100年一遇最大1日降雨量为240.32 mm;同理,采用正态分布求得100年一遇最大15日降雨量为398.84 mm,100年一遇洪峰流量为107.06 m3/s。
计算Copuala函数中的两个参数:肯德尔相关系数(Kendall τ)和联结参数(θ)值见表3和表4。
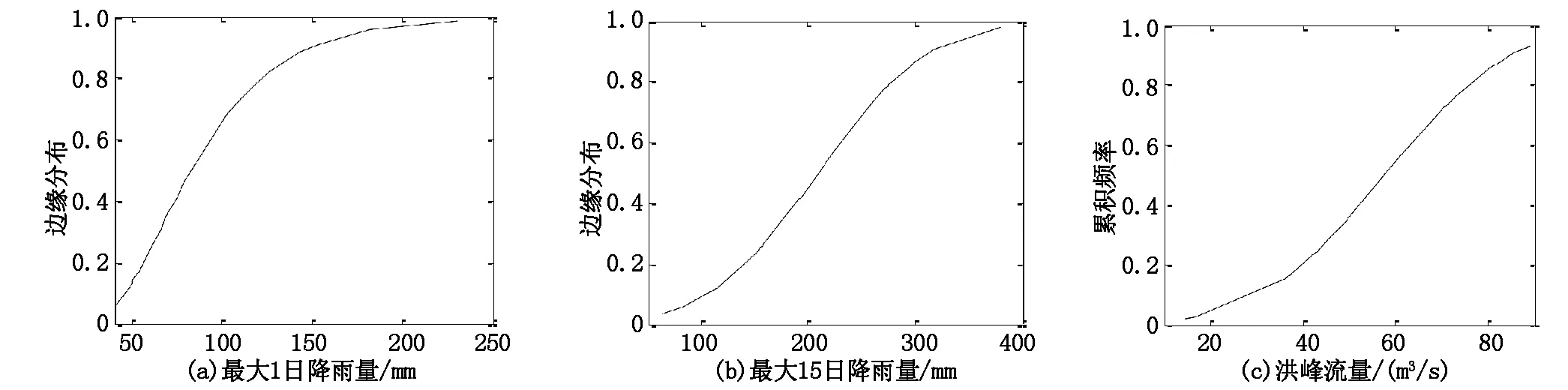
图2 变量边缘分布图

项目最大1日降雨量/最大15日降雨量最大1日降雨量/最大洪峰流量最大15日降雨量/最大洪峰流量肯德尔相关系数0.660.440.54

表4 联结参数值
根据公式(3)计算不同时长各种重现期的降雨量在历史最大和100年一遇洪水中的洪峰流量,见图3。
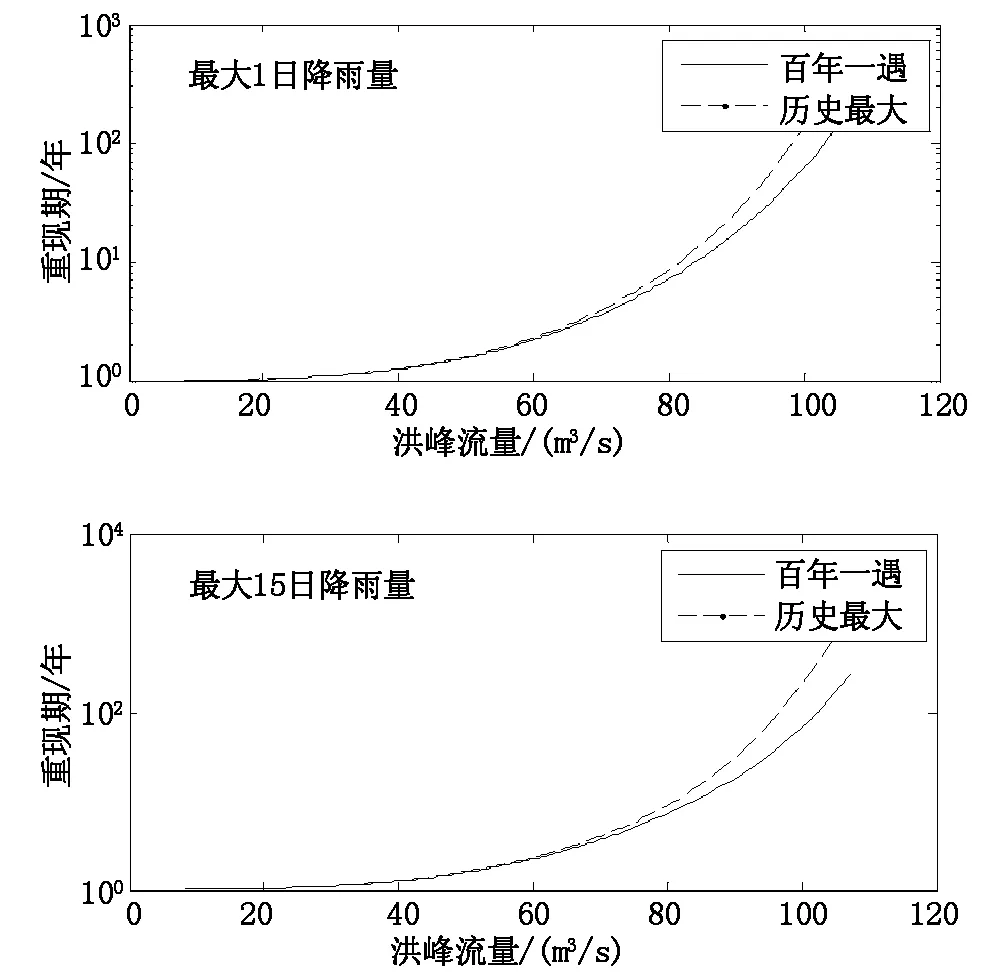
图3 不同条件下最大洪峰流量条件重现期图
4 结 语
正态分布以及对数正态分布较为适合小清河黄台桥洪峰流量以及降雨量分布拟合。
由计算可知,小清河黄台桥站最大洪峰流量与15日降雨量相关性较好,而且根据其得到的条件重现期差别也较大,因此,笔者建议在采用历史洪水加成法分析计算设计洪水时着重以15日降雨为主计算。
这种方法在进行频率分析计算时,考虑了与其相关的非线性因素,更加科学的反映了其相关关系。
[1] DL/T 508/2012电力工程水文技术规程[S].中国计划出版社,2012,北京.
[2] 谷洪钦,王起峰.历史洪水调查在推求设计洪水中的应用[J].山东电力技术,2001(6):50~52.
[3] Sklar,A.Fonctions de repartition a n dimensions et leurs marges[M].Paris:Publ.Inst.Statist.Univ.,1959.
[4] 李小奇,郑东健,鞠宜朋.基于Copula熵理论的大坝渗流统计模型因子优选[J].河海大学学报,2016,44(4):370~376.
[5] 孔祥瑞,陈淑芬,李梅,等.济南短历时暴雨强度公式研究[J].山东建筑大学学报,2013,28(5):445~448.
[6] 吴霞,吴津蓉,李巧,等.新疆汉水泉地区地下水环境背景值计算[J].人民黄河,2015,37(1):83~86.
[7] 张炯,叶琦.基于概率熵判据的大坝位移预警概型比较[J].江西水利科技,2015,6(12):405~409.
[8] Gringorten,I.I.A Plotting rule of extreme probability paper[J].Journal of Geophysystem Resources,1963,68(3),813~814.
[9] 黄华平,梁忠民.多调查期洪水频率计算及参数估计公式推导[J].水文,2016,36(3):1~5.

