基于马尔科夫链的平台生存任务模型与航路评估
李小兵,周新志,宁 芊
(1.四川大学 电子信息学院, 成都 610065; 2.中国电子科技集团公司第29研究所 电子信息控制重点实验室, 成都 610036)
0 引言
在雷达武器威胁环境里,飞行平台通常都需要执行一些任务,比如侦查敌方雷达部署情况,因此飞行平台不仅需要关注自身生存率,同时还要考虑能任务完成的概率。平台的生存率定义为无伤害返回的的概率[1],对于如何有效求解航路上飞行平台的生存率问题,目前的研究还较少,已有的方法主要是直接从平台与雷达武器的距离关系模型来建立生存模型,并在此基础上计算飞行平台的生存率[2-3]。这种方法只考虑了被发现和被打击两种状态,并且模型一旦建立就不容易扩展和修改,更重要的是忽略了状态之间随时间的依赖关系。在任务方面,目前的研究也主要集中在任务规划方面[4-5],在计算任务完成率方面,已有的方法也是使用飞行平台与任务中心的距离来建立任务模型,并在此基础上得到任务完成的概率。
传统方法没能有效刻画生存模型和任务模型,也没能将生存模型和任务模型有机地统一起来,并且无法直观地关注到平台能完成任务且无伤害返回的概率。另外传统方法不能有效地在生存和任务之间权衡,对航路的好坏进行有效评估。近年来,为了突破传统方法的制约,有些学者开始尝试从随机过程的角度来对飞行平台的生存和任务建立模型,其中最有效地便是使用马尔科夫链模型来建立飞行平台的生存模型。
基于马尔科夫链的方法,在最初只建立了来两个状态的生存模型[6],后来发展出了一种五状态的生存模型[7-8]。基于马尔科夫链的生存模型能直观地展现,航路上飞行平台的生存状态概率的变化。但是飞行平台在关注生存的同时还需要考虑完成任务的概率,并且还能关注到不同航路的好坏。为此本文在基于马尔科夫链的生存模型的基础上加入任务模型,并建立生存任务联合模型。在生存任务模型中,能得到无伤害完成任务的概率计算模型。为了度量航路的好坏,在生存任务联合模型的基础上,引入生存代价和任务奖励,从而得到航路的代价,并以此代价度量航路好坏。
1 生存任务模型
1.1 生存模型
为了既能体现飞行平台生存状态的真实性和完整性,又能使建模简单,在此选择5个生存状态。这5个状态分别是未被发现U、被发现D、被跟踪T、参与作战E、被打击H,通常未被发现状态U作为初始状态。H状态是吸收态,因为飞行平台被打击后会一直处于这个状态。生存状态之间是随时间相互依赖的,当平台被跟踪之前需先被雷达发现,平台从被跟踪到被武器击中这一过程中还需经历参与作战这一状态。飞行平台还可以逃离雷达和武器区,逃离时的状态也只能是依次进行,从参与作战状态到未被发现需要依次经历跟踪和被发现两个状态。
刻画生存状态之间的依赖关系,需要用时间连续状态离散的马尔科夫链{X(t)|t>0},其中X(t)代表平台在时刻t的生存状态。时间连续状态离散的马尔科夫链具有马尔科夫性,即过程的将来状态与过程的历史状态无关,只与过程的现在状态有关,其具体定义为式(1):
P[X(t+Δ)=j|X(t)=i]=λijΔ,
(1)
其中:i,j表示生存状态,P是转移概率,λij为转移强度,Δ为无限小时间。马尔科夫性与平台的前后状态转移关系保持了一致。由于马尔科夫性的存在,因此连续时间离散状态的马尔科夫链可充分刻画飞行平台生存状态之间的关系,具体模型如图1所示。在图1中,S表示雷达环境,W表示武器环境,O表示雷达武器之外的环境。
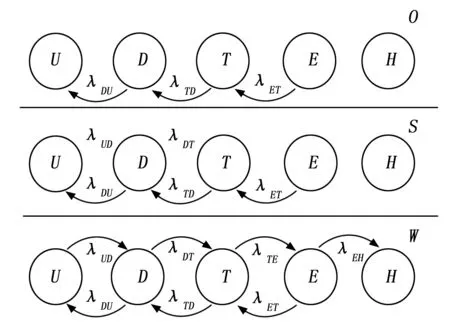
图1 五状态生存模型
1.2 生存任务联合模型
平台完成任务状态也是随机的,对于完成任务状态的模型如图2所示。在图2中,I表示平台还未完成任务,F表示平台完成任务。F是吸收态,因为平台一旦完成任务后就会一直在这个状态,因此不存在从F到I的转移强度。平台在任务执行区域M之外一般不可能完成任务,因此在任务执行区之外λIF=0。

图2 任务模型
为了能使平台关注到完成任务且无伤害返回的概率psm,为此需要将生存模型和任务模型联合起来,具体联合形式如图3所示。图3中包含了所有可能存在的联合状态及状态间的转移关系,总共包含十个状态,UI、DI、TI、EI和HI分别为未被发现、被发现、被跟踪、参与作战和被打击时还未完成任务的状态,同样UF、DF、TF、EF和HF表示为相应生存状态时已完成任务的状态。在联合模型中,状态UI一般作为起始状态。
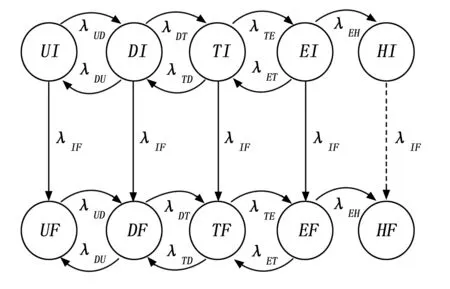
图3 生存-任务模型
在图3水平方向上,生存状态并不取决于是否完成任务,那么此方向的状态转移与生存模型里的状态转移保持一致。在垂直方向上,完成任务的概率并不取决于生存状态,那么此方向的状态转移与任务模型里的状态转移保持一致。当平台处于HI状态时仍有机会转移到HF状态,除非平台完全被击毁。于是在生存-任务模型里,平台完成任务且无伤害返回的概率可表达为式(2):
psm=pUF+pDF+pTF+pEF
(2)
1.3 转移强度与环境
生存任务模型中的转移关系由转移强度λ来刻画。转移强度由飞行平台所在的环境提供,未被标识的转移强度为0,表示此环境下状态转移不可能发生。不同的环境提供不同的转移强度。在环境O里λET>0,λTD>0,λDU>0,其他为0,表示离开雷达武器区域,朝着更安全的状态转移。在环境O的基础上,环境S里增加了λUD>0,λDT>0,表示有被雷达发现和跟踪的可能。环境W在环境S的基础上还提供了λTE>0,λEH>0,表示有参与作战和被打击的可能。
状态转移强度的大小可由1/τij来衡量。在生存模型中,τij反映了地面雷达武器系统的平均反应时间或状态切换时间。在任务模型中,τij表示完成任务所需的平均时间。雷达武器威胁环境,提供的转移强度模型使用三种模型[9]中的常数模型,实际具体的取值应由领域专家给出。
雷达、武器及任务的物理模型,可抽象为二维圆域或三维球域,这样不仅建模简洁,又不会失去对雷达武器主要性质的把握,更多关于雷达武器的模型可参考一些专家的建议[1]。武器通常被探测雷达包围,因为武器需要雷达来探测、跟踪及锁定飞行目标。当然雷达与雷达以及武器与武器之间还可以相互重叠,以表示雷达之间以及武器之间能相互合作,对于在重叠区域的转移强度的计算,可使用已有的方法[9]。另外飞行平台能执行任务的区域,通常被雷达武器包围着,这是符合实际情况的。
2 航路评估
2.1 状态概率计算
为了能评估航路上飞行平台每个状态概率随时间的变化,需要求解状态概率,连续时间离散状态的马尔科夫链框架为求解状态概率提供了解决思路。首先构造转移强度矩阵Λ(t),然后通过求解(3)式所示的微分方程,以此得到状态概率向量p(t)。
(3)
其中状态概率向量p(t)的第j个元素为状态j的概率pj(t),且状态概率向量的初始形式为:
若以Λij(t)来表示转移强度矩阵Λ(t)第i行第j列的元素,则Λij(t)的具体形式为:
由于飞行平台在不同时间可能处于不同的威胁环境里,因此整个飞行航路上的转移强度矩阵Λ(t)是随时间变化的。设威胁环境k里的转移强度矩阵为Λk,时间长度为tn,因而在航路上Λ(t)的取值为:
由于生存任务模型的状态只有十个,是有限数量的,而且Λ(t)在某一时间段里为常矩阵,因此(3)式可用式(4)方法来求解。
p(tn) =eΛn-1 T·(tn -tn-1 )p(tn-1)
(4)
在(4)式中需要求解矩阵指数,对于矩阵Λ的矩阵指数的求解方法为:
2.2 航路代价计算
在得到飞行平台状态概率的基础上,为了在生存和任务两方面度量航路的好坏,在此引入两类代价,一类是单位时间状态保持代价bi,一类是单位时间状态转移代价cij。用v(t)表示在时刻t飞行平台在航路上的期望累积代价,累积代价量化了航路对于飞行平台在生存和任务两方面的好坏。记x(t)=[p(t),v(t)]T,于是有关期望累积代价的微分方程如式(5)和式(6)所示:
(5)
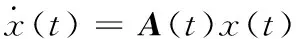
(6)
式(6)中A(t)是一个矩阵,其具体形式为:
求解式(6)使用式(7)所示的迭代方法。
x(tn) =eAn-1 ·(tn -tn-1 )x(tn-1)
(7)
代价参数bi是关于平台生存状态的代价。bH*=0,因为H是吸收态,当平台处于此状态便不再离开。当平台处于U状态时,这时对于平台来说是很安全的,因此bU*=0。当平台处于其他生存状态时,应当假定bE*≥bT*≥bD*≥0,因为平台处于状态D、T和E时,受到的威胁逐渐增强。代价参数cij是关于生存状态转移的代价参数,其中cE*,H*≥0,其他生存状态转移的代价为0,因为其他生存状态转移代价可归于状态代价。对于任务状态转移来说,平台从未完成任务转移到完成任务状态的过程,应当得到dF的奖励,dF的大小衡量了任务的重要性。于是航路评估就可以在生存和任务之间进行权衡,比如在任务区,即使生存率会很低,如果任务很重要,则可能dF>cE*,H*。代价参数具体描述如式(8)和式(9):
b=[0,bD*,bT*,bE*,0]
(8)
(9)
3 仿真设计与结果分析
3.1 场景设置与仿真结果
图4展示了一个二维场景,在此场景中放置了三个雷达和两个武器,并放置了两条航路和两个任务区,任务和武器都被雷达覆盖。两条航路的起点均为(0,0),终点均为(300,-25),航路2是由航路1通过改变有限个路标点的Y方向的值得到,并以两条航路中间的公共点作为分界点将航路分成前段和后段。
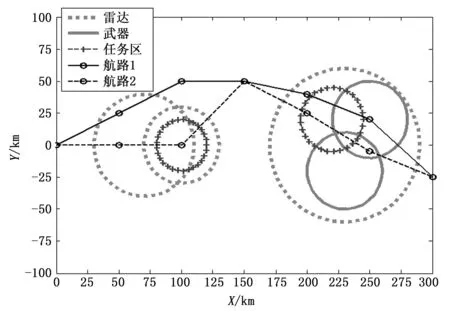
图4 包含航路、雷达武器及任务的场景
环境O、S、W及M中的转移强度设置如表1所示,平台生存代价参数的设置如表2所示。平台在0.3个单位时间(min)里以1.2 km的航程速度飞行。仿真结果中,图5至图8分别显示了平台在航路1和航路2上状态概率随时间的变化,图中的曲线代表状态概率面积图的外侧轮廓线。图9显示了两条航路上完成任务且无伤害返回概率的变化。图10显示了完成任务的奖励值dF分别取0、50、300和600时两条航路上的代价变化。
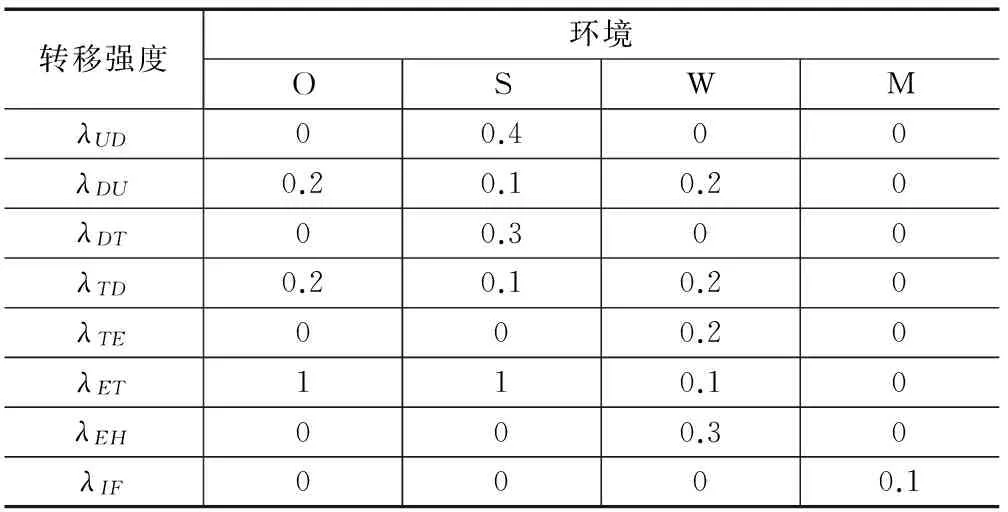
表1 转移强度设置

表2 生存代价参数设置

图5 航路1有关任务未完成状态的概率

图6 航路1有关任务完成状态的概率
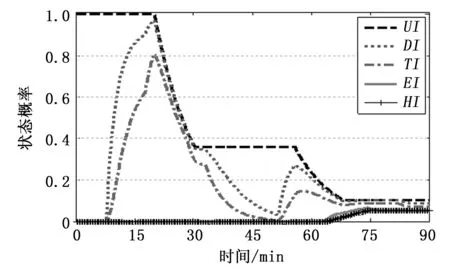
图7 航路2有关任务未完成状态的概率
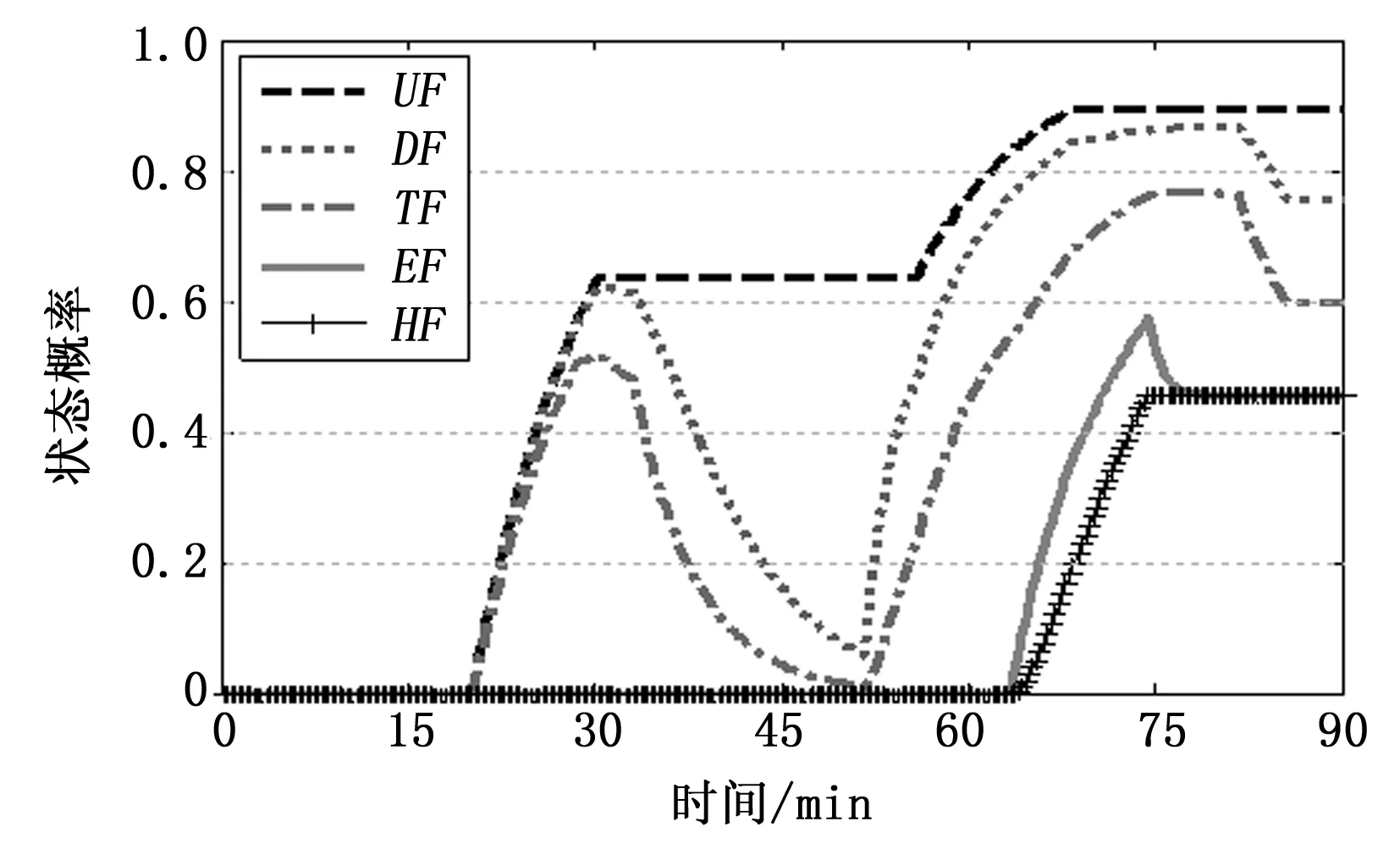
图8 航路2有关任务完成状态的概率
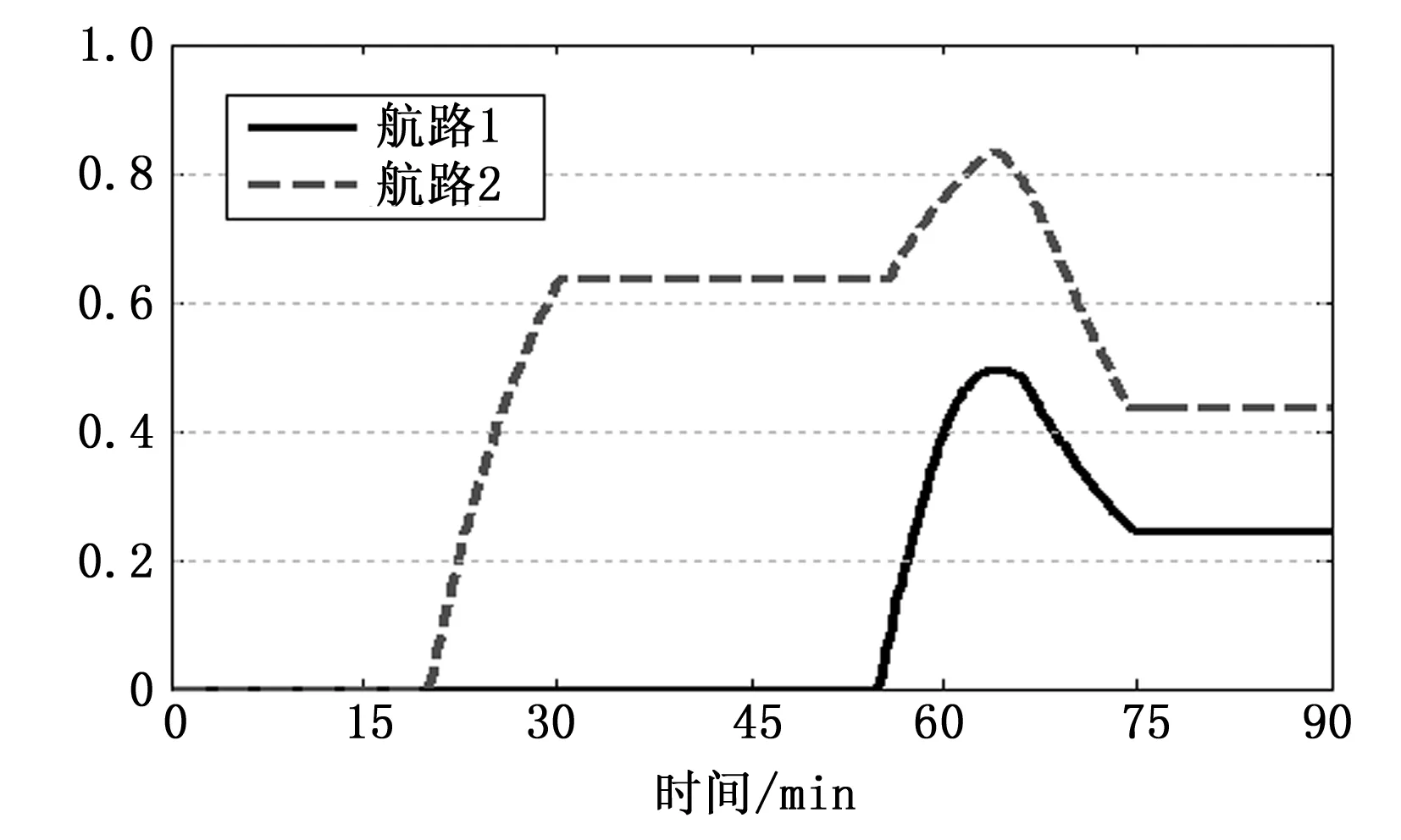
图9 完成任务且无伤害返回概率
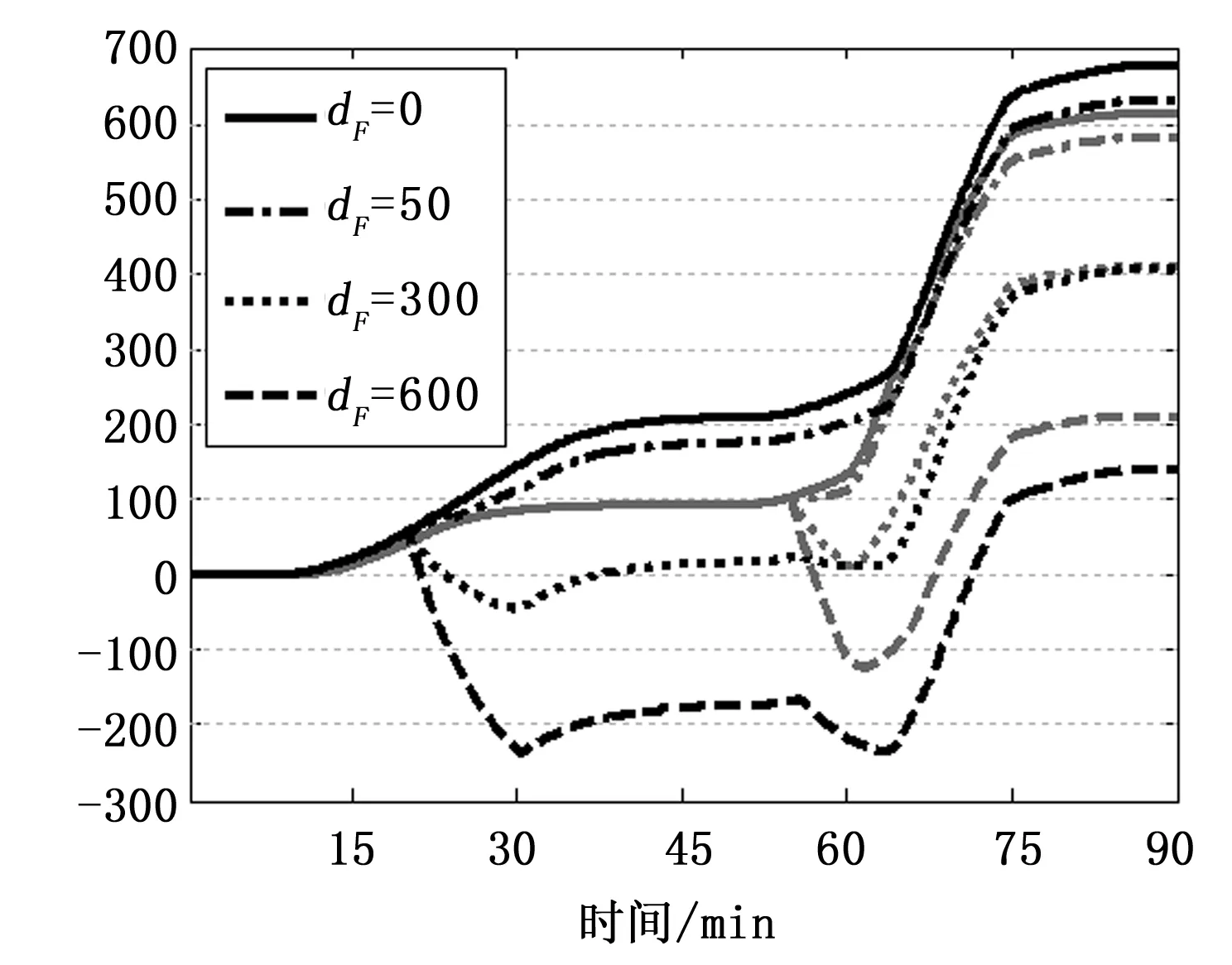
图10 不同dF值时航路1(黑色)和 航路2(灰色)的代价变化
3.2 结果分析
图5至图8的状态概率变化反映了两条航路所经过的环境。最开始平台处于环境O,这时只有UI状态,当飞行平台进入雷达环境S时,有关生存状态D和T的概率迅速增加,而关于作战E和被打击H状态只在平台进入武器环境W里发生。当平台经过任务区M时,关于完成任务F状态的概率开始增加。
在航路的前一段,航路2比航路1关于DI和TI的状态概率增加得更多。这与航路2的前段经过两雷达的重叠区相一致,因为在雷达重叠区具有更强发现和跟踪能力。在航路的后一段,虽然航路2经过了武器重叠区,但最终航路2与航路1的被打击时已完成任务HF状态概率相差不大,这与两条航路后段经过相同的任务区,且两武器区有相同的最好武器相一致。
从任务状态概率来看,在图6和图8中,航路2比航路1关于完成任务F的状态概率多一次增加的过程。这与航路2比航路1在前段多经过一个任务区相一致。从图9中的完成任务且无伤害返回的概率上看,航路2比航路1多一次上升过程,这与航路2的前半段经过了一个任务区区相一致。在终点时,航路2的psm明显大于航路1的psm,从这个角度来说,航路2好于航路1。如果平台很注重能完成任务且能无伤害返回,那么此时就可为飞行平台提供决策支持。
从psm的角度不能完全衡量航路的好坏,因为不能在任务和生存之间进行权衡。图10显示了不同dF值时两条航路累积代价的变化,其中较粗的黑实线是航路2的代价曲线,灰色曲线代表航路1的代价曲线。dF的不同取值衡量了任务相对生存的重要性。当不考虑任务只考虑生存时,航路2的累积代价更高,此时航路1优于航路2。当dF=50时,航路2与航路1的代价都有所降低,且它们之间的差距在缩小,但航路2的代价依然高于航路1的代价。当dF=300时,两条航路最终的代价几乎一样,此时两条航路无明显好坏。当dF=600时,航路2的代价明显比航路1的代价低,这时航路2反而比航路1更好。
4 结论
本文采用马尔科夫链的方法,将飞行平台的生存和任务看作是随机过程,并分别对生存和任务来建立模型,然后有效统一生存模型和任务模型。在生存任务模型的基础上,对计算航路代价,并以此代价有效地衡量了航路有关生存和任务两方面的好坏。基于马尔科夫链的方法能直观地展现了状态和航路代价随时间的变化,也展现了不同航路上能完成任务且无伤害返回的概率变化,并对航路进行有效评估。状态概率、航路代价都可为飞行平台在生存和任务两方面提供决策支持。
[1] Helldin T,Erlandsson T. Automation guidelines for introducing survivability analysis in future fighter aircraft[A]. Proceedings 28th Congress of International Council of the Aeronautical Sciences[C]. Brisbane,Australia:ICAS,2012:1-10.
[2] 郭凤娟,张 安,张耀中,等. 高空无人侦察机生存力仿真研究[J]. 西北工业大学学报,2009,27(6):827-832.
[3] 李寿安,宋笔锋,李东霞. 飞机在单个射弹打击下的生存概率分析[J].哈尔滨工业大学学报,2009,41(3):121-124.
[4] 蔡凌峰,傅爱萍,成海东. 无人机任务动态重规划方法[J].指挥信息系统与技术,2013,4(6):31-36,79.
[5] 罗 贺,秦英祥,王国强,等. 一种无人机侦察能力评估模型[J].火力与控制指挥,2016,41(2):7-12.
[6] Erlandsson T,Niklasson L. An air-to-ground combat survivability model[J]. Journal of Defense Modeling and Simulation: Applications,Methodology,Technology,2015,12(3):273-287.
[7] Erlandsson T,Niklasson L. Comparing Air Mission Routes from a Combat Survial Perspective[A]. Proceedings of the 26th International Florida Artificial Intelligence Research Society Conference[C]. Palo Alto,California:AAAI Press,2013:58-63.
[8] Erlandsson T,Niklasson L. Automatic evaluation of air mission routes with respect to combat survial[J]. Information Fusion,2014,20(11):88-98.

