转轨时期我国高铁定价的双层规划模型分析

高广阔+单永恒+肖刚

摘要：相较于市场化定价的公路和民航运营方式，高铁的定价方式是致使其处于亏损状态的最大原因。文章根据综合效用理论、广义出行费用，综合考虑高铁票价、乘客机会成本、运输方式舒适性与安全性，运用竞争性定价的理论，建立双层规划模型。以此分析我国高铁定价存在的问题，并通过对京沪线以及广深线的分析，给出转轨时期我國高铁票价制定的最优策略。

关键词：转轨时期；综合效用理；广义出行费用；双层规划模型

2013年国务院机构改革方案公布，决定撤销铁道部并拆分成国家铁路运输管理局和中国铁路总公司，这标志着我国铁路改革进入“政企分开、网运分离、客运与货运分离”的市场化转轨时期。然而现实并非如此，在我国交通运输领域，公路和民航已基本实现了市场化定价的运营，而影响力重大的高铁大多处于亏损状态，其定价机制仍然是严格执行政府定价，相关定价机制过于单一，尚未建立健全价格听证会制度。

实质上，仍然延续以往列车客运的垄断定价方式，不能体现市场化定价原则，也未能充分发挥高铁作为高效运输工具的社会价值，达到帕累托最优，因此高铁票价定价机制亟需完善。国内外学者对定价理论进行了很多研究：Hjoon Chang（2001）通过对不同运输方式供给、需求和节点约束的研究，构建了以时空网络结构为基础，以运输价格和时间价值为自变量的运输定价竞争模型，并通过实践估算出了韩国交通运输市场上高速铁路的市场占有率情况；Daniel V（2004）重点研究了泛欧长途客运体系中传统交通方式与高铁及民航的市场竞争关系，构建了多变量博弈定价模型；陈建华（2004）认为：铁路票价的制定要考虑来自竞争对手的竞争和旅客的选择行为等因素；Javier Campos（2009）分析了全球多个高铁发展状况，对影响定价的诸多因素（运营模式、维护成本、社会福利及高铁的外部性因素）进行了综合研究，并构建了基于空间网络平衡的定价模型；姜琪（2012）分析了高铁与高速公路的垄断竞争关系，提出了放开铁路价格约束政策建议；张旭（2012）分析了武广沿线自高铁开通运行以来与民航的竞争情况，运用Binary Logit模型对高铁与民航的竞争程度进行了量化测度，提出高铁与民航应该协调发展避免陷入恶性竞争；总体来看，国内外专家从市场竞争的角度分析了铁路的定价问题，但是大多都集中与单一竞争对手的分析，而对转轨时期高铁定价研究较少。目前在我国的高速客运领域，已经形成了高铁、航空和高速公路的市场竞争格局；高铁与航空、高速公路等的竞争日益激烈，这决定了转轨时期我国高铁定价需要考虑竞争对手的价格策略。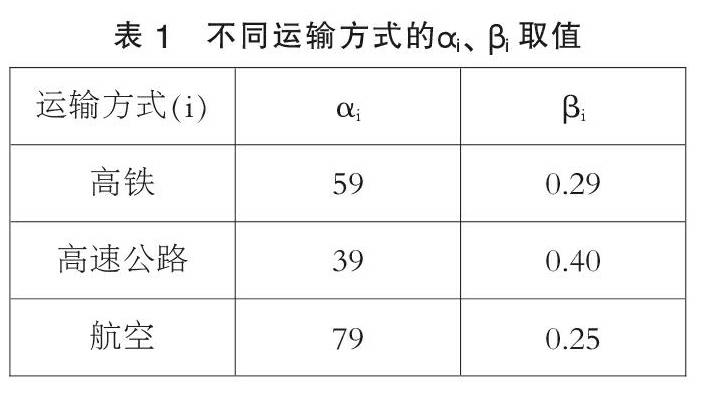

本文在阐述我国高速客运领域的市场发展现状和铁路转轨时期的特点基础上，综合考虑高铁运营企业自身的发展、民航和高速公路的博弈竞争态势以及旅客的选择效用，构建竞争性定价模型，并对高铁运营企业与民航、高速公路运营企业之间的价格博弈进行分析，得出转轨时期我国高铁票价的最优定价策略。

一、理论基础

（一）竞争性定价理论

竞争性定价就是运输企业根据自身在运输市场竞争格局中的定位，合理制定价格以实现利润最大化的目标。竞争性定价包括通行价格定价和排他型定价。通行价格定价是指根据市场通行的价格水平来制定企业票价，其出发点是谨慎保持与竞争者之间的价格关系，避免企业间的恶性竞争。排他型定价是把价格作为竞争的主要手段，期望利用合理价格战胜竞争对手，从而获取更大的市场份额。

（二）综合效用理论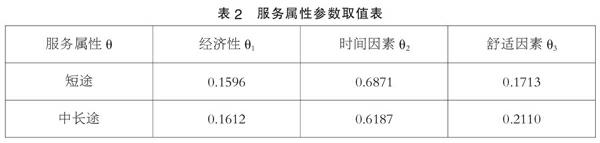

效用是用来衡量消费者在消费时获得的满足感。在交通运输领域，综合效用就是指旅客结合自身的预算、目的地和出行距离等因素做出选择后从所选的交通方式上获得的满足感。综合效用函数是基于票价、时间成本、舒适性、安全性等因素构建的。

1. 总票价

总票价J主要包括市内公交费用和主要交通运输工具的票价。由于市内公交费相较于其他费用较少，这里不作考虑。因此，旅客使用第i种主要运输工具的总票价为Ji。

2. 机会成本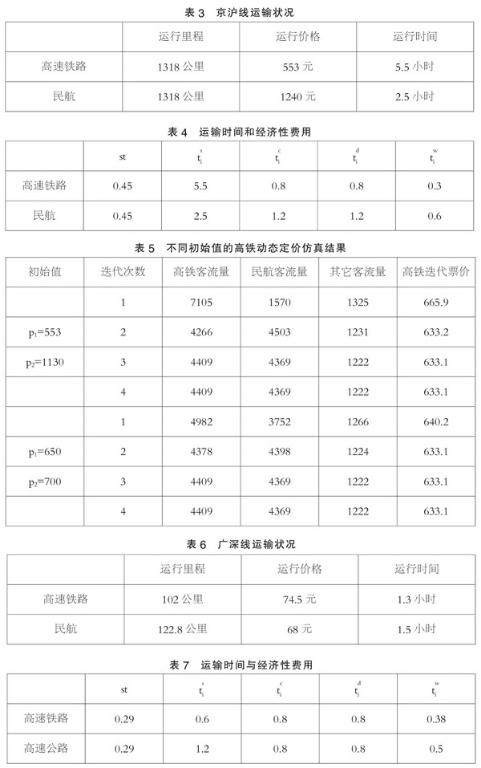

由于很多旅客都具有劳动力的属性，出行者在出行过程中的时间如果用来投入生产，可以产生一定的产出，因此其乘坐时间会产生机会成本，可以用如下公式表示：

其中 Ti—出行产生的总机会成本；

st—单位时间的机会成本；

t—交通工具i的运行时间；

t—出发地市内公交时间；

t—目的地市内公交所时间；

t—旅客在区间出发车站内的等候排队上车时间

st—单位出行时间的机会成本为，其计算公式如下：

其中， GDP表示地区生产总值；

N表示地区劳动力人数；

Ta表示特定区域劳动者每年的劳动时间。

通常在高铁的运营过程中，中途换乘的概率较低，因此本文在计算旅客单位出行时间机会成本时只考虑出发地与目的地两个城市的单位时间价值，求其平均值近似表示地区间旅客单位出行时间价值。

3. 舒适性

本文在舒适性与旅客的疲劳感之间建立函数关系，将舒适性转化成疲劳程度再转换成恢复疲劳所需的时间，然后用时间成本来测度舒适性。从人的生理角度来看，恢复疲劳所需的时间是有上限的，暂取24小时，同时恢复疲劳所需时间与旅行距离呈曲线关系，可用如下公式表示：

其中， T——第i种交通工具恢复疲劳所需要的时间；endprint

LT——恢复疲劳所需的时间极限，为24小时；

根据张铱莹，彭其渊（2006）的研究，不同运输方式的舒适性函数中αi、βi的取值如表1所示。

恢复疲劳所需的时间转换成可测量的成本：

4. 安全性

安全性在旅客选择运输方式的过程中具有较大的影响，但交通运输工具的安全性难以转换成实际成本。为此，我们采用乘法原则将安全性转化为系数纳入旅客的选择效用函数中，其中高铁为0.99，高速公路为0.95，民航为0.99。

至此，已经初步确定了影响效用函数的各参数测度的具体数量形式，为了进一步建立完整的效用函数，在兼顾加法原则与乘法原则优点的基础上将安全系数指标和费用测度指标综合起来形成效用函数。本文建立的费用函数形式如下：

其中， θ1、θ2、θ3表示不同运输方式的服务特性参数。本文参考了孙朝苑（2004）研究成果，计算出各种运输状态下各种服务的θ结果如表2所示。

（三）广义出行费用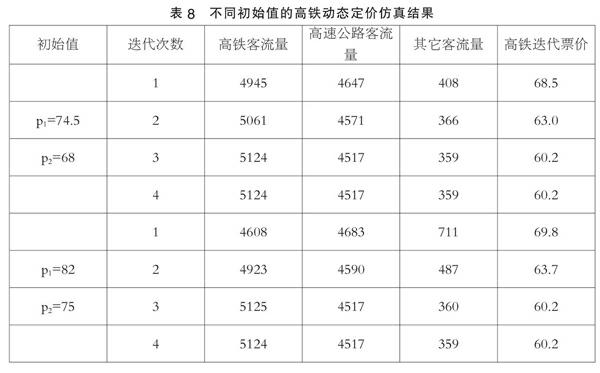

旅客在出行时有多种运输方式可以选择，除了考虑自身的出行性质和收入水平外，还会对各种运输方式的速度、客流量、时间、经济、方便以及舒适等因素进行综合权衡，这些因素带来的成本或者效用通常称为广义出行费用，一般广义出行费用函数可采用幂函数的形式来表示，在本文中。

二、模型建立

基于竞争性定价理论，本文拟构建双层规划模型分析转轨时期高铁的定价策略。双层规划模型最早由Bracken和McGil（1973）提出，通常是指具有上下两个不同层次约束条件的决策模型，先由处于领导地位的上层决策者作出决策，接着处于下层的决策者跟随做出相应的决策。而后经过反复进行决策方案的调整，直到上、下层都不愿意对其决策进行调整为止。此时模型就达到一个相对平衡的状态，而促使模型达到平衡状态的方案称为相对最优方案。

在上层规划（6）中，高铁运营企业在兼顾政府规制、成本和市场需求的条件下制定合理的票价方案，以保证自身的经济效益最大化。其中F代表高铁企业的利润函数，该函数与高铁运营企业的总收入p1×q1以及总成本c×q1有关。pmin，pmax分别表示高铁运营企业的边际成本和政府规制的最高票价，高铁客运企业在此票价区间进行价格决策。

下层规划（7）则体现了在多种高速客運交通方式竞争条件下，旅客对不同运输方式的选择，其目标是使每个出行者的广义出行费用最低。其中S（q）=a0q表示虚拟客流的阻抗函数，用来衡量除高铁和航空外其它运输方式对旅客选择行为的影响。fn（q）=aq-Vn表示旅客的广义出行费用函数，其中a，b为待定参数，该函数与客流量成正相关，与旅客在不同的客运方式中获得的效用Vn负相关。

通过上述模型的构建，求出在航空机票价格一定时高铁票价的最优解。同理也可建立当高铁票价固定时，航空客运的定价优化模型：

求解双层规划问题的关键在于找到连接上下层模型的反应函数q（p）的具体形式，本文将通过灵敏度分析方法的启发式算法来进行求解。灵敏度分析的核心在于通过Jacobian矩阵变换求解出客流需求对票价的导数关系，从而得到反应函数的一阶泰勒展开式：

将（10）式代入到上层目标函数中，上层规划模型就转换成了一个普通的非线性优化问题，通过现有的方法即可求解。另外，由于本文中构建了高铁和主要竞争对手的两个双层规划模型，在求出各自的最优解的同时还需要进行新一轮的博弈，直到得到博弈的均衡解。

三、仿真实验

考虑到不同距离的旅程，高铁面临的市场竞争对手是不一样的，本文选取了中国经济最发达的北京至上海、广州至深圳这两个区间的高铁进行研究，广深线距离较短，且广州到深圳没有民航运输，其主要竞争对手在于高速公路，而京沪线距离较长，其主要竞争对手来自于民航。此外，本文假定旅客的旅程都是直达的，不考虑中途换乘情况。

（一）京沪线

1. 经济性费用

京沪高铁二等坐票价格为553元，而京沪间民航经济舱的全额票价约为1240元，考虑到民航运输通常在网上会有一定的折扣，我们假定为0.68折，即为847元，同时参考已有研究，计算出高铁运营的平均成本为0.45元/公里，航空运营的平均成本为0.43元/公里。

2. 时间成本

由于各运输方式的出发具体地点不同，因此本文根据实际情况直接给出乘客出行过程中所使用的时间以及旅客出行单位时间机会成本：

根据（1）式可得，旅客乘坐高铁的时间机会成本为：T高铁为333元，旅客乘坐高速公路客运的机会成本T民航为247元。

根据上述数据，我们可以建立广深沿线高铁与高速公路的费用函数：

通过Maple和Lingo软件对模型进行编程求解，得到如下不同初始值的高铁和航空票价组合的运算结果，如表5所示。

从表5中的数值结果可以看到，在完全信息的条件下，如果让高铁与航空企业进行自由竞争，经过4次迭代，运算的结果收敛，高铁的最终的票价趋于均衡的稳态，稳态时的高铁票价收敛于633元，比目前票价高15%，同时高铁的客运量高于民航的客运量。

（二）广深线

1. 经济性费用

广深高铁D字头二等坐票价格为79.5元，G字头二等坐票价格为74.5元，在这里我们取较小的G字头票价74.5元作为广深高铁运输票价J，折合成每公里运价约为0.73元。广深之间直达的高速公路票价维持在68元左右，折合成每公里运价约为0.55元。

2. 时间成本

旅客出行过程中各种时间以及单位机会成本为：

按照公式（1）可得旅客乘坐高铁的时间机会成本为：T高铁为72.5元，旅客乘坐高速公路客运的机会成本T公路为95.7元。endprint

根据上述数据，可以建立广深沿线高铁与高速公路的费用函数：

通过Maple和Lingo软件对模型进行编程求解，得到不同初始值的高铁和高速公路票价组合的运算结果，如表8所示。

从表8中的数值结果可以看到，在短距离的广深线运输通道中，如果让高铁与高速公路客运进行自由竞争，经过4次迭代，运算的结果收敛，高铁的最终的票价趋于均衡的稳态，稳态时的高铁票价收敛于60.2元，平均每公里定价为0.58元/人，低于现行的每公里0.73元/人。广深高铁还存在这一定幅度的降价空间。

四、结论

本文以短距离的广深线和长距离的京沪线为例，对我国交通运输行业中高铁与其它运输方式之间的竞争问题进行了研究，运用综合效用函数和双层规划模型，最后得到了一个合理的高铁客运票价。

1. 对于短距离运输，高铁的主要竞争对手为高速公路，高铁的运输速度快，安全性高，高速公路运输灵活，乘坐方便。由于两者的票价相差不大，高铁与高速公路形成了非常激烈的竞争。同时在短途运输中，高铁的舒适性等优势难以得到很好的发挥，从影响旅客的出行选择因素来看，票价成为了首要的考虑因素，高铁要想吸引到更多的客流，就必须调整票价，对广深高铁来说，当高铁的运价下降一定幅度能够赢得与运输能力相匹配的客流量。

2. 对于中长距离的客运运输，高铁的主要竞争对手为民航。在与民航的竞争中高铁的安全性和便捷性等因素得到了很好的体现，但在快捷性等方面存在着一定的差距，由此给旅客带来的时间机会成本也较大，需要通过票价的调整来弥补旅客由此带来的时间成本，同时民航灵活的定价机制也对高铁客流量带来了很大的影响。

五、政策建议

1. 根据市场环境动态调整价格。高铁在短距离与长距离运行时面临的市场竞争环境是不一样的，针对不同的竞争主体，高铁需要及时的调整其定价策略。例如民航在中长距离运输领域是高铁的主要竞争对手，它的定价策略非常灵活，能够根据市场的需求情况及时的调整票价。高铁的定价也需要时时关注市场竞争对手票价的变化灵活的进行调整以增强同民航的竞争力，既可以避免高铁运输资源的浪费实现自身的盈利目标，同时又促进了全社会交通资源的优化配置，提高了社会总体福利水平，间接的实现了其公益性的目标。

2. 实行差异化定价。差异性定价主要体现在地域方面，由于我国幅员辽阔，区域经济发展长期不平衡，东部地区经济發达，交通网络密集，居民收入较高，居民出行的可选择运输方式多样，同时高铁的运营成本也相对较高。而对于欠发达地区，居民收入相对较低，交通网络相对较少，居民可供选择的交通运输工具相对较少，随着高铁的开通其它运输工具的减少，有些地区出现了“被高铁”的现象，针对不同区域的高铁运营线路，应允许根据具体的情况实行不同的定价方案。

参考文献：

[1]Hjoon Chang. A network-based model for market share estimation among competing transportation models in a regional corridor[D]. University of Maryland. 2001.

[2]Daniel van Vuuren. Optimal pricing in railway passenger transport： theory and practice in the Netherlands[J]. Transport Policy，2002（02）.

[3]陈建华，高自友.铁路票价制定策略和线路提速方案的优化分析[J].管理科学学报，2004（04）.

[4]Javier Campos，Gines de Rus.Some stylized facts about high-speed rail： A review of HSR experiences around the world[J].Transport Policy，2009（16）.

[5]姜琪.网络型产业的有效竞争研究[J].经济管理研究，2012（02）.

[6]张旭，栾维新，赵冰茹.基于非集计模型的武广高铁与民航竞争研究[J].交通运输系统工程与信息，2012（06）.

[7]张铱莹，彭其渊.客运专线对运输通道分担率的影响[J].铁道运输与经济，2006（28）.

[8]姜达.基于不同运输方式竞争的高速铁路票价定价方法研究[D].西南交通大学，2014.

[9]孙朝苑.客运专线对沿线城市铁路客运量分流问题的研究[J].铁道经济研究，2004（03）.

[10]Bracken J and McGill J T. Mathematical Programs with Optimization in the Constaints[J]. Operations Research，1973（21）.

[11]Bard J F. Practical Bilevel Optimization： Algorithms and Applications[M]. Dordrecht： Kluwer Academic，1998.

[12]Colson B， Marcotte P， Savard G. An Overview of Bilevel Optimization[J]. Ann Oper Res，2007（153）.

基金项目：国家社会科学基金项目“基于大数据关联分析的中国雾霾污染问题统计研究”（15BTJ017）。

（作者单位：上海理工大学管理学院）endprint