渐缩异径弯头展开放样新方法研究

翟英俊，陈承宪，刘 杉，王伟民

(中国电力工程顾问集团东北电力设计院有限公司，吉林 长春 130021)

1 概述

渐缩异径弯头是一种直径逐渐缩小的弯头，可用来连接不同管径的管道，渐缩异径弯头的特殊形式使得其在电厂中得到广泛应用。在水泵吸水管中常用其代替弯头及吸水喇叭口，在空冷塔中常用两个渐缩异径弯头做成Y型三通。实际上，在有弯头和变径管的组合处都可考虑应用渐缩异径弯头，这样不仅能减少一个管件，还会使水力条件变得更好。这种弯头结构相对复杂，是弯头放样中最难的一种。虽然已有相关文献和书籍对其展开图画法进行过介绍，但或多或少存在着操作困难、计算复杂、计算精度不够等缺点。经过对多个工程案例的比较和摸索，本文提出一种新的渐缩异径弯头展开图放样方法。一改以往建立几何关系的复杂方法，采用建立方程组解直线交点的准确计算方法来确定渐缩异径弯头的几何数据，并通过简单的Autolisp语言将渐缩异径弯头展开图在AutoCAD中自动绘制出来。

图1 渐缩异径弯头

2 技术背景

由于正圆锥被平面斜切后切口的形状为椭圆，所以当一个正圆锥被斜切成两半后，将其中的一半以原轴线为中心旋转180°仍然可以将这两半拼到一起。见图2，当锥形管被4个平面斜切后，将2、4号短管旋转180°就可将5个短管拼成见图1的渐缩异径弯头。

图2 正锥形管

当管径较小时我们可以通过切割圆锥管的方式制造渐缩异径弯头。但对于大管径渐缩异径弯头来说则存在着如下问题：

(1)一般大管径的弯头需要的圆锥管较长，可能会超出卷管机的最大宽度；

(2)一般标准钢板的宽度有限，需要多个钢板焊接拼成较长的锥形管，用拼接成的锥形管切割制造弯头可能会出现十字焊缝；

(3)大管径锥形管切割非常困难，不易操作也难以保证切割精度。

综上，探索渐缩异径弯头展开图做法是非常有必要的。

3 新的展开图计算方法

本文以90°渐缩异径弯头为例对新的展开图计算方法进行阐述。一个分成五瓣的90°渐缩异径弯头由两个端节和三个中间节组成。已知条件为转弯半径R，进出口半径r2，r1。由已知条件可推出切割面与端面的夹角γ为

切割面之间的夹角为2γ

端节轴线高度为h，中间节轴线高度为2h。

在知道这些条件的情况下，我们将图2中的正锥形管放入直角坐标系中(见图3)。将两个端面的圆周16等分，a4为端面A的一个等分点，过a4点做垂线交a1a9于c4点，过b4点做垂线交b1b9于d4点，连接c4d4交e1e9于e4点，c4e4为展开图(见图4)中f4h4在平面上的投影，下面主要阐述f4h4的求解过程。f4h4为空间直线，如果分别知道f4、h4的空间坐标，则可求得

c4、e4为f4、h4在xoy平面上的投影点，所以f4、h4和c4、e4的x，y坐标是相同的。

由图3可知，

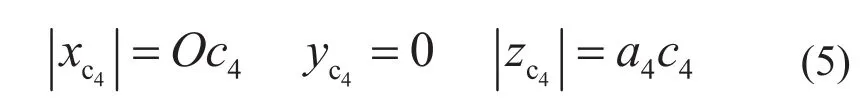
c4点的x，y，z坐标为

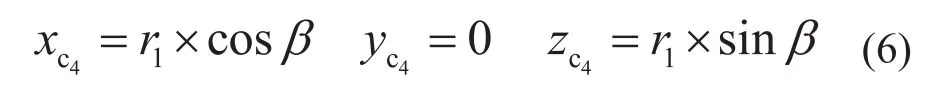
同理可知，d4点的x，y，z坐标为

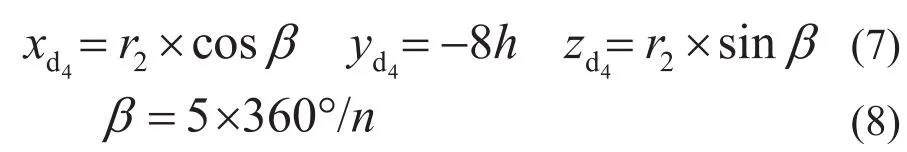
式中：n为展开图的等分数，本文中n=16。

e4点为直线e1e9与c4d4的交点，e1e9与c4d4

为直角坐标系中的两条直线，

其直线方程分别为：

通过(2)～(10)可以求出交点e4的x、y坐标分别为

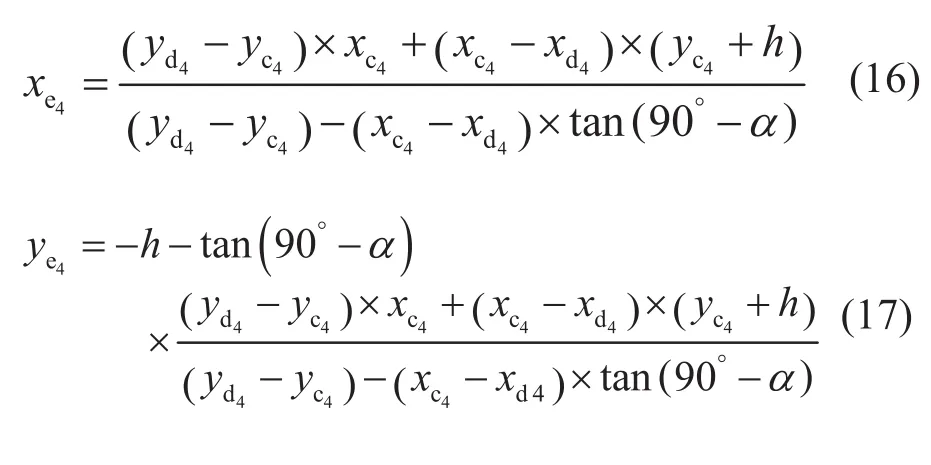
e4点的z坐标可通过半径为mm1的圆求得，而mm1的长度等于m1点x坐标的绝对值，所以只需将m1的y坐标代入直线a1b1的直线方程中便可求出m1的x坐标，进而可确定

mm1值。a1b1的直线方程为

因为m1的y坐标等于e4的y坐标，所以将ye4代入(8)可得

k0、p0的求取方法同k1、p1。

e4点的z坐标可通过下式求得

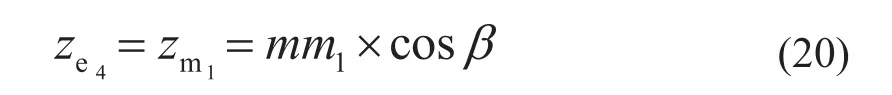
综上，我们得到了空间点f4，h4的坐标分别为(r1×cosβ，0，r1×sinβ)，(xe4，ye4，ze4)。将其代入式(4)便可求出空间直线f4h4。同理，可 求 出f1h1、f2h2……f9h9、f1i1、f2i2……f9i9……f1g1、f2g2……f9g9，从而也就确定了展开图中的h1i1、h2i2……h9i9、i1j1、i2j2……i9j9……n1g1、n2g2……n9g9的长度。

以上的计算过程通过Excel中的函数可以很方便的实现。在计算过程中可将渐缩异径弯头的角度、转弯半径、切割面个数、进出口半径以及圆周等分数作为变量，实现对任意渐缩异径弯头展开图的快速计算。

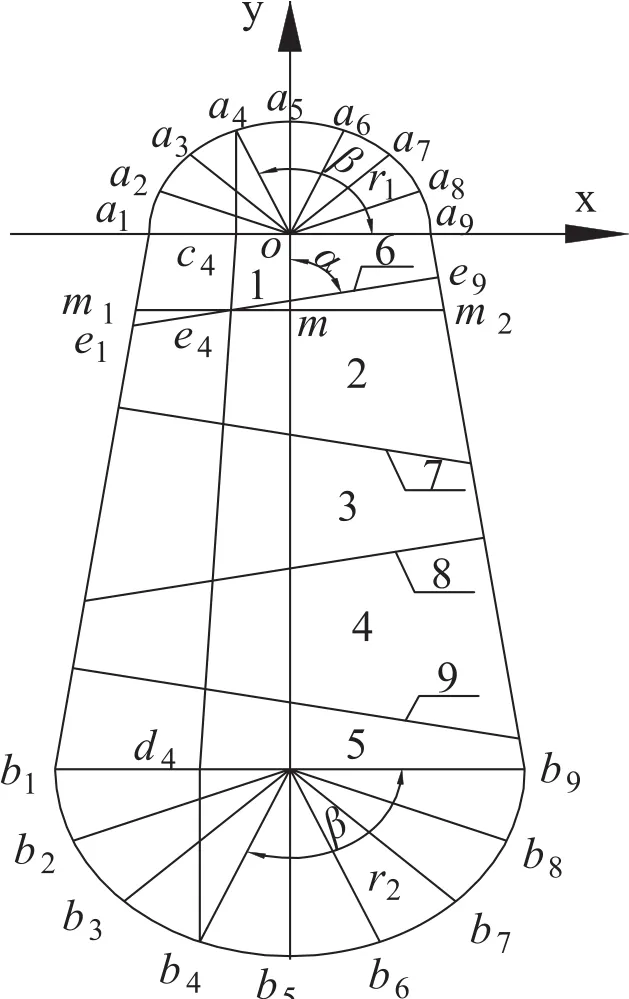
图3 直角坐标系中的锥形管

图4 渐缩异径弯头展开图

4 应用AutoCAD自动绘制展开图

在得到展开图的数据之后，可以应用简单的Autolisp程序将展开图绘制到AutoCAD中。下面以绘制h1h2……h9为例进行阐述。h1h2……h9上的点可以通过极坐标的形式表示，极坐标的表示形式是(x＜a)。h1点可表示为

f1h1在前面已经求得，R1为圆锥管顶点到小圆的母线长

ε为展开图顶角16等分后的角度

Autolisp程序有一定的格式要求，在输入的过程中可以通过Excel中的“concatenate”命令将括号、空格、双引号等与计算出来的数据结合到一起，这样可以大大减少输入量。绘制曲线h1h2……h9的程序如下：

将上面这段Autolisp程序加载到AutoCAD中后，在命令行输入“zhankaitu”，AutoCAD就会自动绘制出曲线h1h2……h9。按照同样的方法便可以将展开图中的曲线都绘制到AutoCAD中。

5 新方法的特点

有关书籍和论文所阐述的关于渐缩异径弯头的展开方法主要包含“绘图法”和“计算法”。“绘图法”大多存在着工作量大、操作困难、精度低等缺点。从以往的经验中可以知道当进出口管径相差较小时锥形管顶点到锥形管的距离较大，在绘图的过程中需要不断的缩小和放大图形，操作起来非常困难甚至会出现捕捉错误。当锥形管进出口圆周等分数超过32份时再用“绘图法”就更加困难，“绘图法“难以提高展开图的精度，对于大管径的展开图可能会产生较大的误差。

通过“计算法”来绘制展开图能够克服上述问题。常规的 “计算法”大多是建立空间线段与已知条件间的几何关系，过程相对复杂且通用性不强，仅适用于锥形管中间节的轴线长度相等并且等于端节轴线长度2倍的情况。如此，锥形管的长度被固定，导致渐缩异径弯头适用的灵活性变差。而本文介绍的计算方法是一种通过求取空间点坐标来计算空间线段长度的方法。按此方法，对锥形管的切割位置并无严格限制，从而提高计算方法的使用范围。与此同时，计算得到的数据还可被用于Autolisp程序中，实现在AutoCAD中自动绘图，使得展开图的绘制变得方便快捷。

6 结语

本文提出的展开图计算和Autolisp程序在AutoCAD中自动绘制展开图方法不仅克服了“绘图法”的一些缺点，也是对“计算法”的一种优化，可以提高展开图的精度，减小误差并实现自动绘图。本文所阐述的渐缩异径弯头展开图计算方法突破了传统计算思路，通过解方程求取交点确定空间线段的坐标进而求取长度，一改以往建立几何关系的复杂方法，使得展开图的绘制在理解上和计算上都更加容易，这对于改进其他类型管件展开图的计算方法有一定的启发意义。

[1] 刘萍华． 牛角弯头三维CAD展开放样[J]．现代制造工程，2008，(12)．

[2] 王力夫． 钣金工艺中渐缩管弯头的近似展开理论研究 [J]．锻压技术，2006，(5)．

[3] 翟洪绪． 钣金展开计算法[M]．北京：机械工业出版社，2005．