水电机组轴系电磁振动特性实测与仿真分析

王 宾,党晓强,徐 永,3

(1.四川水利职业技术学院羊马校区,四川 成都 611231; 2.四川大学水利水电学院,四川 成都 610065;3.西华大学流体及动力机械省部共建教育部重点实验室,四川 成都 610039)

电磁振动是电机相关领域比较重要的研究课题之一,对于水电机组轴系的振动特性有较大的影响,会加重轴系的振动摆度问题,甚至造成定、转子之间的碰磨,严重影响机组的安全稳定运行[1-4]。在众多电磁因素引起的振动激励中,最常见的是由电机磁路和电路的不对称引起的不平衡磁拉力。

为了仿真研究不平衡磁拉力对水电机组轴系电磁振动特性的影响,通常需要建立计算模型[5]。计算模型主要分为机组轴系模型和不平衡磁拉力分析方法两部分,目前不平衡磁拉力的分析方法大致可以分为3类:①简化为一个负刚度系数[6],即认为不平衡磁拉力与转子偏心率呈线性关系;②利用简化分析方法,考虑不平衡磁拉力与转子偏心率等影响因素的非线性关系[7-8];③利用有限元方法计算磁场区域获得不平衡磁拉力[9]。第一类方法主要适用于机组设计阶段时对磁拉力的估算,但不能考虑励磁工况变化对磁拉力大小的影响;第二类方法从宏观角度出发,考察不平衡磁拉力与转子偏心率等因素的非线性变化关系,对于研究电磁力影响下的机组振动特性目前具有较大的优势;第三类方法从微观角度出发,能够考虑包括励磁工况变化在内的众多影响因素对磁拉力的影响,其不足之处是计算量过大,若以考察电磁力引起的机组振动响应为研究目标,则该类方法因为在计算的实时性方面要求过高而难以适用。对于机组轴系模型的建立,由于Jeffcott转子模型易于分析,考察不平衡磁拉力影响时,多数学者以此模拟机组轴系[7-8],但这种模型由于过于简化而无法正确反映真实机组的振动特性。目前机组轴系模型中,应用广泛且行之有效的是有限元转子模型[10-11]。

以往对于水电机组轴系电磁振动的研究主要集中在理论计算分析方面,而与实测分析相关的研究较少。本文通过某水电站125 MW半伞式两导轴承轴流转桨式水电机组(以下简称研究机组)现场变励磁试验数据的详细分析,总结了由电磁因素引起的振动特性变化规律，再利用仿真分析方法对电磁力引起的振动特性变化的原因进行了分析。

图1 现场变励磁试验振动状态过程

1 现场变励磁实测数据分析

为了排查水电机组轴系的振动是否主要由电磁因素引起,一般需要对机组进行变励磁试验。通过改变励磁工况(励磁电流)的方式,考察机组振动对励磁工况的改变是否敏感,据此判断振动原因是否为电磁因素。

水电机组的变励磁试验一般使机组运行在未加励磁、加100%励磁或加50%励磁的工况下。未加励磁时,发电机为空转工况,此时机组不受磁拉力的作用。通入励磁电流而定子绕组开路时为机组的空载工况,此时发电机中只有励磁电流产生的励磁磁场,励磁电流的大小决定了励磁磁场的强度,从而决定交界面上磁应力的大小。定、转子的相对偏心会引起不平衡磁拉力,正常运行工况下,越大的励磁电流将引起越强的不平衡磁拉力;而该不平衡磁拉力反过来作用于转子,对轴系的振动特性产生影响。这类振动问题对励磁工况的变化敏感,正是利用这一特性,可以通过变励磁试验的方法排查是否为电磁因素引起的机组振动。

通过分析变励磁试验时的现场振动数据,可以对比机组在有无不平衡磁拉力影响下的振动特性,从而识别由不平衡磁拉力引起的振动特性变化。图1所示为研究机组变励磁试验时的现场振动数据[12],该电站的在线监测系统在上导、水导两轴承处设置了振动位移传感器。由于整个试验过程在空载工况下进行,有功功率始终为零。从图1可以看出,在励磁电流发生变化时,上导轴承y方向摆度峰峰值及上机架水平振动y方向摆度峰峰值的变化明显(x方向上的情况与此类似,图1中列出)。励磁电流的增大将明显增大上导轴承处的振动摆度。而水导轴承处受励磁电流改变的影响并不显著,甚至有略微减小的趋势。

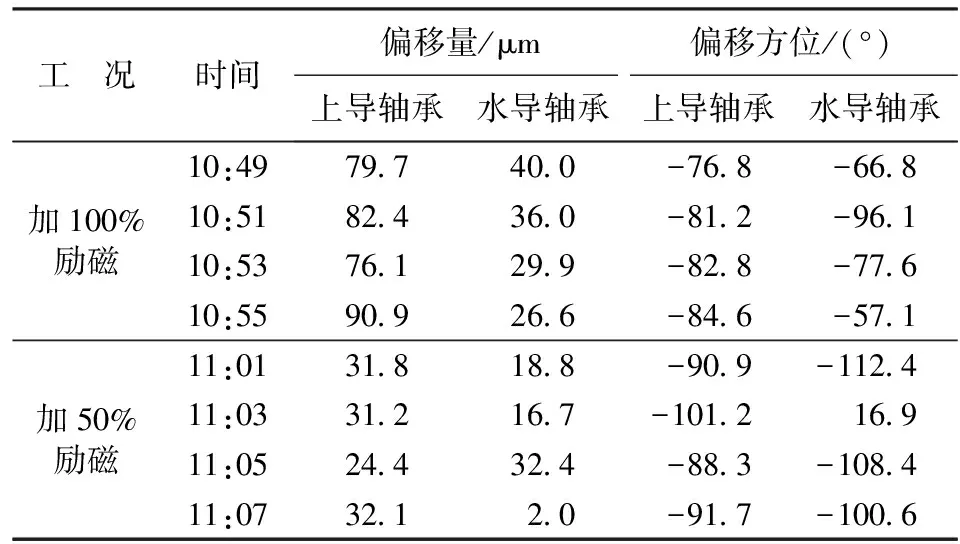
以未加励磁时的轴心轨迹中心作为参考中心,图2为加100%励磁后某时刻的大轴姿态及相应时间段的轴心轨迹。可以看出,加100%励磁后,轴心轨迹中心发生了明显的偏移,其中上导轴承处的偏移量更大。为了判断这种轴心轨迹中心的偏移是否具有规律性,统计图1所示的变励磁试验过程中不同励磁条件下轴心轨迹中心偏移的大小及方位如表1所示(其中加100%励磁时的统计数据取自10:48—10:57,加50%励磁时的统计数据取自11:00—11:08)。由表1可以看出,在同一励磁工况下,上导轴承处的轴心偏移量及偏移方位相对比较稳定,不同时刻的轴心偏移量及偏移方位基本保持一致,而水导轴承处则没有明显的规律。此外,轴心轨迹中心的偏移量随励磁电流的增大而增大,而偏移方位也会发生微小变化。

图2 加100%励磁后的大轴姿态及轴心轨迹

工 况时间偏移量/μm偏移方位/(°)上导轴承水导轴承上导轴承水导轴承加100%励磁加50%励磁10：49797400-768-66810：51824360-812-96110：53761299-828-77610：55909266-846-57111：01318188-909-112411：03312167-101216911：05244324-883-108411：0732120-917-1006

由以上分析结果,可推断不平衡磁拉力对水电机组轴系电磁振动特性的影响:①上导轴承处的振动摆度峰峰值明显增大;②轴心轨迹中心向某一方位发生偏移;③偏移量与不平衡磁拉力大小成正比。

2 仿真模型的建立

2.1 不平衡磁拉力分析模型

转子匝间短路、铁磁材料磁化不均匀以及定、转子相对偏心等都会导致定、转子间气隙磁场的不对称,从而引起不平衡磁拉力。当定、转子中心存在大小为e、方位为γ的偏心时(图3),转子圆周上气隙厚度δ为空间角度α的函数:

δ=δ0-ecos(α-γ)

(1)

式中δ0为均匀气隙厚度。忽略铁磁材料磁阻影响时,气隙磁密Bδ的分布与气隙厚度有如下关系

(2)

式中:μ0为空气磁导率:Fδ为发电机气隙的基波合成磁势。由式(1)可知,最小气隙厚度出现在转子偏心方位上。而由式(2)可知,气隙厚度越小,气隙磁密越大,由于Fδ是一个行波方程,气隙磁密Bδ在转子圆周上的分布也是一个行波方程。

图3 定、转子偏心示意图

在定、转子间气隙与铁磁材料交界面上,单位面积上的磁应力T的计算公式为

(3)

对式(3)在整个气隙圆周上积分得

(4)

式中:Fump为转子圆周上所有磁应力的总和;R为转子半径;L为定子铁芯有效长度。气隙均匀的情况下,因为转子的对称性,Fump为零。当Fump不为零时,即为不平衡磁拉力。

气隙磁密的差异是导致不平衡磁拉力的主要原因,确定气隙磁密分布是计算不平衡磁拉力的关键。当考虑饱和效应的影响时,必须考虑铁磁材料的磁化特性,在这种情况下,很难得到如式(2)的解析表达式。一般退而求其次的分析方法是通过曲线拟合及磁路简化计算等方法对磁回路中所有铁磁材料的磁化特性进行分析,从而考虑饱和效应影响[13-14]。本文利用发电机空载特性曲线分析计算不平衡磁拉力。由于励磁电流与气隙磁密具有一一对应关系,利用空载特性曲线信息能够得到励磁电流If与气隙磁密Bδ的N次多项式拟合函数关系[11]:

(p0-If)=0

(5)

式中:N为拟合多项式幂次;p0、p1、…、pN为拟合多项式的系数。求解不同气隙厚度和励磁电流时的多项式方程,可求得相应情况下的气隙磁密大小,代入不平衡磁拉力计算公式(式(4))即可求解此时的不平衡磁拉力大小。该分析方法既简化了分析过程,又能够考虑励磁电流变化对不平衡磁拉力的影响,计算精度和效率也都能满足轴系响应分析的需求。

图4为研究机组在图3所示相对偏心情况下的气隙厚度分布与某时刻气隙磁密分布情况。水电机组一般为凸极转子,这里为了简化分析,忽略了凸极磁极之间的间隙引起的气隙厚度突变。气隙磁密分布在整个转子圆周上的周期数与磁极对数相同,最大气隙磁密与最小气隙厚度相对应。

图4 相对偏心下气隙厚度与气隙磁密分布

2.2 机组轴系模型

对于水电机组轴系动力特性而言,不平衡磁拉力作为边界激励力作用在发电机转子处。为了研究其对水电机组振动特性的影响,需建立机组轴系模型。图5为研究机组的轴系计算模型示意图,对其沿轴线进行有限单元离散化,利用Lagrange方程或Hamilton原理导出单元的运动方程,再将单元运动方程按节点坐标关系叠加,即可组成整体机组轴系的运动微分方程组,这里每个节点包括2径向位移自由度及2角位移自由度共4个自由度。数学微分方程可表示为

(6)

式中:M、C、K分别为系统质量矩阵、阻尼矩阵和刚度矩阵;q为包含所有自由度的广义坐标向量;Fu为作用于转子节点的不平衡磁拉力向量;F0为不平衡磁拉力以外的其他受力向量,包括轴承力、质量不平衡力等。质量不平衡力的计算公式比较成熟,轴承力一般简化为常刚度阻尼系数,这种处理方法过于简化。本文采用文献[10]所述的轴承力处理方法,能够考虑轴承力在响应计算过程中的变化,更加符合实际的振动响应规律。式(6)所描述的轴系动力学模型可通过Wilson-θ等数值积分方法进行求解。

图5 机组的轴系计算模型示意图

在仿真分析中,F0作为在仿真计算过程中总是存在的受力施加于机组轴系相应节点上,而前述能够考虑励磁电流变化的不平衡磁拉力Fump在仿真分析中根据仿真需要进行相应的变化,以考察电磁因素变化对机组轴系电磁振动响应的影响。

3 仿真验证

图3所示定、转子偏心为静态偏心形式,一般是指由制造缺陷导致的定子内圆和转子外圆不正以及安装不当等因素引起的定、转子间不同心。而在机组旋转运动过程中,由于转子质量偏心的存在,质量不平衡力会使得转子在运转中偏离其理想中心,这种偏心形式称为动态偏心。两种偏心形式在水电机组的实际运行中是同时存在的。为了考察两种偏心形式对机组轴系电磁振动特性的影响,本文利用仿真计算模型分别分析动态偏心、静态偏心及两者共同作用情况下,不平衡磁拉力对机组轴系电磁振动特性的影响。

3.1 只考虑定、转子动态偏心

首先假设定、转子间仅存在动态偏心,此时转子轴系在质量不平衡力的作用下绕其理想中心涡动,上导轴承及水导轴承处的轴心轨迹如图6所示(图中“*”为参考中心,“o”为仿真工况下的轴心轨迹中心。图7、图8同)。转子的涡动会导致定、转子间最小气隙厚度发生变化,进而导致不平衡磁拉力发生变化。图6(b)为额定励磁工况下仅考虑动态偏心时的上导轴承振动响应轴心轨迹，可以看出,励磁工况下上导轴承处的摆度幅值有所增加,而水导轴承处未见明显变化(图6(d)),两导轴承处的轴心轨迹中心均未发生偏移。

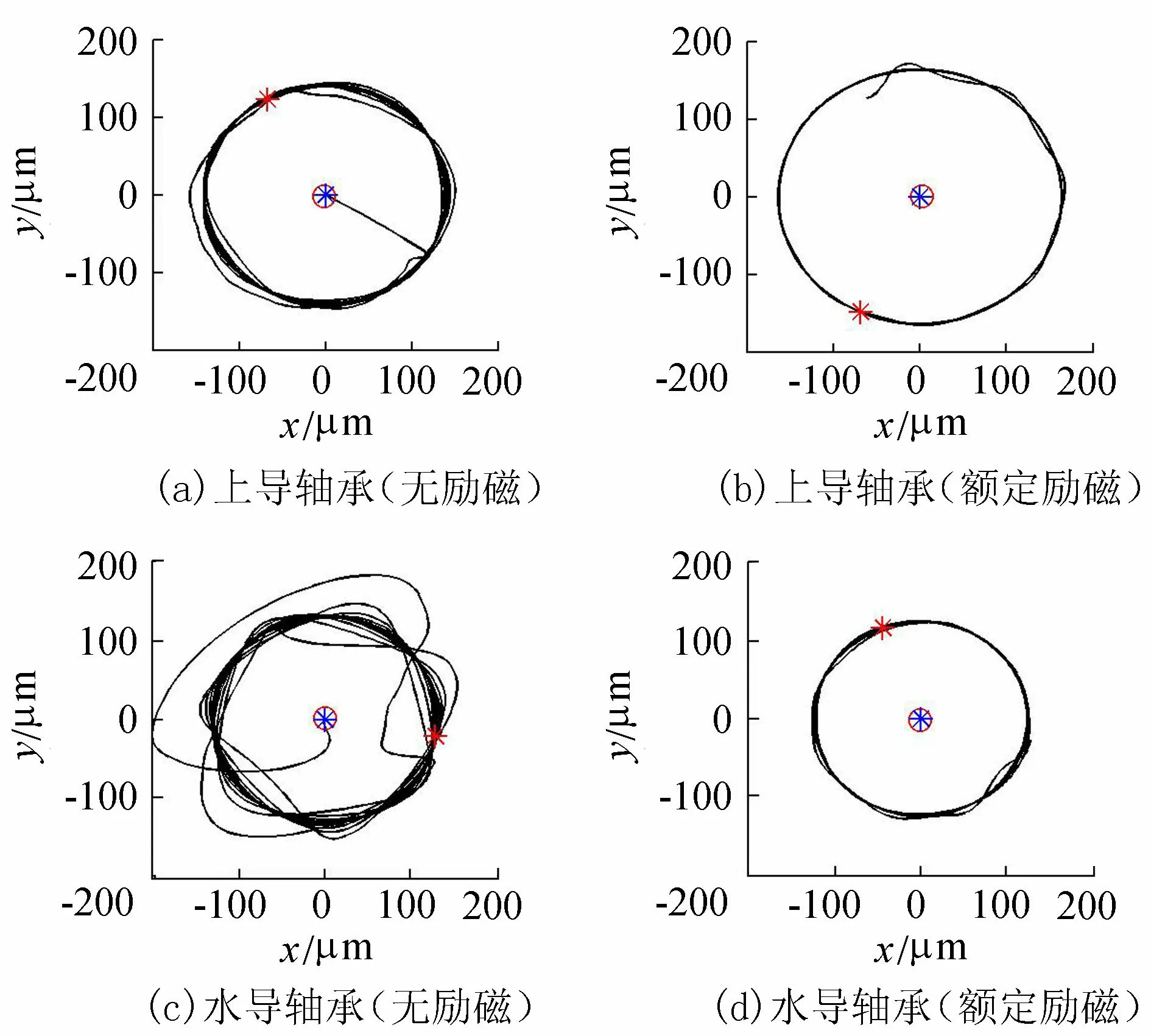
图6 只考虑动态偏心时的轴心轨迹变化

3.2 只考虑定、转子静态偏心

若只考虑定、转子间的静态偏心,则由此引起的最小气隙厚度在固定的方位,此时不平衡磁拉力的方向固定。参照表1的统计分析结果,假定存在静态偏心值为0.2 mm,方位为-80°,图7所示为只考虑定、转子间静态偏心时,不平衡磁拉力对轴心轨迹影响的仿真结果,与图1所示实际变励磁试验的工况变化一致。可以看出,受不平衡磁拉力的影响,轴心轨迹向静态偏心方位发生了偏移,该偏移量大小与加励磁大小成正比,即励磁电流越大,轴心轨迹中心的偏移量越大。水导轴承处轴心轨迹的变化规律与上导轴承处相似,也发生了一定轴心轨迹中心的偏移。

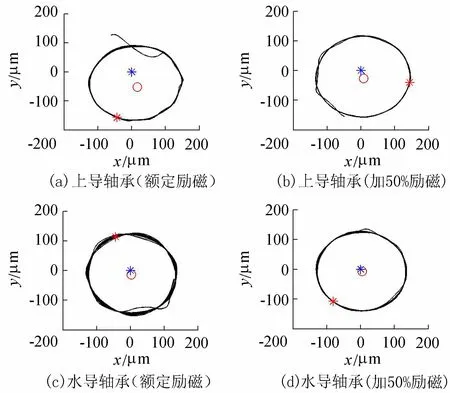
图7 只考虑静态偏心时的轴心轨迹变化

3.3 同时考虑两种偏心形式

若同时考虑两种偏心形式的一般情况,则两种偏心形式共同决定了定、转子间气隙的分布情况,从而决定该情形下不平衡磁拉力的变化规律。图8所示为同时考虑两种偏心形式时不平衡磁拉力对轴心轨迹影响的仿真结果,也与图1所示实际变励磁试验的工况变化一致,这里也分别考虑了额定励磁和加50%励磁两种工况条件下的仿真分析结果。从图8可以看到,对比图6(a)和图6(c)的结果,同时考虑两种偏心形式的仿真结果综合了分别考虑两种偏心形式时的振动特性,即上导轴承处的摆度幅值增大,而两导轴承处的轴心轨迹中心均发生朝某一特定方位的偏移,偏移量的大小与励磁电流大小成正比。

图8 同时考虑两种偏心形式时的轴心轨迹变化

利用仿真计算模型,可以仿真模拟图1所示的实际变励磁试验,仿真计算结果在两导轴承节点处的振动摆度峰峰值变化规律如图9所示,仿真试验的励磁电流工况与现场变励磁试验相同,依次为无励磁、加100%励磁和加50%励磁,每个工况下仿真时间为16 s。仿真计算结果的摆度峰峰值变化趋势与现场数据吻合得很好。上导轴承处的摆度峰峰值随励磁电流增大而明显增大,而水导轴承处的摆度峰峰值并无明显变化,甚至有略微的减小。

图9 变励磁试验仿真

从以上仿真分析结果可知,电磁因素对水电机组振动特性有明显的影响。其中由定、转子间的动态偏心引起的不平衡磁拉力导致机组上导轴承处的摆度增大,而由静态偏心形式引起的不平衡磁拉力将导致机组轴心轨迹中心发生偏移。定、转子间动态偏心的主要作用是增大了电磁振动增幅值,而静态偏心的贡献在于使转子轴系发生朝某一特定方位的轴心偏移。这一振动规律与研究机组轴系两导轴承布置的结构形式相关,但可以推断,定、转子间的两种偏心形式对电磁振动特性的影响规律具有一般性。

4 结 语

本文从实测变励磁试验数据分析和仿真计算两个角度讨论了水电机组轴系电磁振动特性的变化规律。实测变励磁试验数据分析显示,电磁因素对研究机组轴系电磁振动特性的影响主要有:上导轴承处的摆度增大,轴心轨迹中心朝某一方位发生偏移且偏移量随不平衡磁拉力的增大而增加;水导轴承处的轴心轨迹中心偏移方位与上导轴承处相似,但偏移量较小,且其摆度并未增大,反而有略微减小的趋势;由于布置得离发电机转子较远且受水力因素影响较大,不平衡磁拉力引起的水导轴承处振动特性变化相对较小。

仿真计算分析发现,上导轴承处摆度的增大是由定、转子动态偏心引起的不平衡磁拉力造成的,而轴心的偏移是由静态偏心引起的不平衡磁拉力造成的。实际机组工作过程中同时存在静态偏心及动态偏心两种偏心形式,所以加励磁后同时出现上导轴承处摆度增大及轴心偏移的现象。水导轴承处的摆度略有减小的振动特性变化也与现场数据吻合,这一特定变化规律与研究机组的轴系结构特性有关。仿真计算分析结果与实测数据分析结果吻合较好,验证了实测变励磁试验数据分析中统计发现的振动特性规律,并找出了相应的激振原因,较好地揭示了水电机组轴系电磁振动现象产生的原因。

[1] 白晖宇,荆建平,孟光.电机不平衡磁拉力研究现状与展望[J].噪声与振动控制,2009,29(6):5-7.(BAI Huiyu,JING Jianping,MENG Guang.Survey and outlook on the research of the unbalanced magnetic pull in the motors[J].Noise and Vibration Control,2009,29(6):5-7.(in Chinese))

[2] 张礼达,任腊春.水电机组状态监测与故障诊断技术研究现状与发展[J].水利水电科技进展,2007,27(5):85-89. (ZHANG Lida,REN Lachun.Current research and develpment of state monitoring and fault diagnosis of hydropower units [J].Advances in Science and Technology of Water Resources,2007,27(5):85-89.(in Chinese))

[3] 张志诚,陈广洲.三峡工程左岸电站机组调试动力响应分析[J].水利水电科技进展,2005,25(3):55-57.(ZHANG Zhicheng,CHEN Guangzhou.Dynamic response analysis of start-up operation for unit regulation of left bank power station of Three Gorges Project[J].Advances in Science and Technology of Water Resources,2005,25(3):55-57.(in Chinese))

[4] 张思青,沈东,王晓萍,等.水力机组轴向振动机理分析研究[J].水利水电科技进展,2004,24(1):40-43.(ZHANG Siqing,SHEN Dong,WANG Xiaoping,et al.Study on mechanism of axial vibration of water-turbine generator units[J].Advances in Science and Technology of Water Resources,2004,24(1):40-43.(in Chinese))

[5] PENNACCHI P.Computational model for calculating the dynamical behaviour of generators caused by unbalanced magnetic pull and experimental validation [J].Journal of Sound and Vibration,2008,312(1/2):332-353.

[6] BETTIG B P,HAN R.Modeling the lateral vibration of hydraulic turbine generator rotors [J].Journal of Vibration and Acoustics-Transactions of the ASME,1999,121(3):322-327.

[7] 张雷克,马震岳,宋兵伟.水轮发电机组在不平衡磁拉力及密封力下振动特性分析[J].水电能源科学,2010,28(9):117-120.(ZHANG Leike,MA Zhengyue,SONG Bingwei.Characteristics analysis of hydroelectric generating set under unbalanced magnetic pull and sealing force of runner [J].International Journal Hydroelectric Energy,2010,28(9): 117-120.(in Chinese))

[8] 宋志强,马震岳.考虑不平衡电磁拉力的偏心转子非线性振动分析[J].振动与冲击,2010,29(8):169-173.(SONG Zhiqiang,MA Zhenyue.Nonlinear vibration analysis of an eccentric rotor with unbalance magnetic pull [J].Journal of Vibration and Shock,2010,29(8):169-173.(in Chinese))

[9] LUNDSTRÖM L,GUSTAVSSON R,AIDANPJ O,et al.Influence on the stability of generator rotors due to radial and tangential magnetic pull force[J].IET Electric Power Applications,2007,1(1):1-8.

[10] XU Y,LI Z H,LAI X D.Simulation model of radial vibration for a large hydro-turbine generator unit and its application[C]//IEEE Power Engineering and Automation Conference.New York:IEEE,2012:191-195.

[11] 徐永,李朝晖.利用发电机空载特性曲线的不平衡磁拉力分析方法[J].大电机技术,2012(2):1-5.(XU Yong,LI Zhaohui.Analytical method of the unbalanced magnetic pull taking advantages of the open-circuit characteristic of a generator [J].Large Electric Machine and Hydraulic Turbine,2012(2):1-5.(in Chinese))

[12] LI Z H,AI Y Z,SHI H X.Optimal maintenance information system of gezhouba hydro power plant[C]//IEEE Power Engineering Society General Meeting. New York:IEEE, 2007: 1-5.

[13] PERERS R,LUNDIN U,LEIJON M.Saturation effects on unbalanced magnetic pull in a hydroelectric generator with an eccentric rotor [J].IEEE Transactions on Magnetics,2007,43(10):3884-3890.

[14] OHISHI H,SAKABE S,TSUMAGARI K.Radial magnetic pull in salient pole machines with eccentric rotors [J].IEEE Transactions on Energy Conversion,1987,2(3):439-443.