土石山区山坡降雨入渗产流模型
甘永德,刘 欢,贾仰文,顾金普,仇亚琴,司曼菲
(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京 100038;2.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100; 3.天津科技大学海洋与环境学院,天津 300222)
山坡是流域水文响应的基本单元,是水文过程发生的重要场所。探索和认识山坡上的降雨入渗产流过程是进行流域分布式水文模拟的基础,对指导流域水资源评价、管理和水土保持建设具有重要意义。受到气候和下垫面条件等多种因素的影响,山坡降雨入渗产流过程十分复杂,基于物理实验,使用数学模型对这一过程进行模拟分析,是研究山坡降雨入渗产流机理的有效手段[1-2]。Philip[3]假定山坡为由均质土壤组成的平面斜坡,改进了其在1957年提出的入渗模型。Troch等[4]提出了山坡蓄量Boussinesq方程,Hilberts等[5]将一维山坡蓄量Boussinesq方程与一维Richards方程相耦合,进一步提高了山坡壤中流模拟效果。Chen等[6]将Green-Ampt方程扩展到了山坡尺度,量化分析了坡度对入渗产流的影响。Hopp等[7]开发了一个简化的宏观感知模型,探究了山坡降雨产流的阈值问题。Liao等[8]利用基于物理机制的山坡水文模型HYDRUS-2D,模拟评估了山坡产流对降雨、土壤物理性质和土地利用类型的敏感性。国内方面,胡堃等[9]使用Horton模型模拟入渗和地表产流过程,用水箱模型模拟壤中流过程,分析了华北石质山区的坡地产流特征。穆天亮等[10]基于长历时Philip积水入渗公式,建立了黄土坡面降雨入渗产流模型。刘贤赵等[11]分析了黄土坡面降雨入渗产流中的滞后机制,建立了考虑滞后作用的入渗产流模型。陶汪海等[12]通过联立Green-Ampt方程、运动波方程及泥沙输运方程,利用数值求解的方法模拟了坡地的产流产沙过程。刘昌明等[13]基于Green-Ampt模型提出了GAF降雨产流模型。然而,目前大多数山坡降雨入渗产流模型将山坡土壤看作均质土壤,没有考虑土壤中碎石的存在对山坡入渗产流过程的影响。另外,在模型模拟中,山坡基岩层多被处理为不能储水的斜面层。因此,这些山坡降雨入渗产流模型在土石山区的适用性有所不足。
本文基于对土石山区山坡下垫面特性的认识,一方面引入碎石体积比例系数Rv量化土壤中碎石的存在对山坡土层入渗产流的影响,另一方面,考虑山坡基岩凹凸面及封闭裂隙的储留,加入了基岩凹凸面及封闭裂隙储留计算模型,构建了土石山区山坡降雨入渗产流模型,并验证了模型的合理性和有效性。
1 土石山区山坡降雨入渗产流模型构建
1.1 模型分析
1.1.1 土石山区山坡下垫面特性
在土石山区,山坡下垫面从上到下由枯枝落叶层、土壤层和基岩裂隙层组成。其中,根据土壤中含有的碎石含量及风化程度等的不同,土壤层进一步分为均质土壤层、土石二元混合介质层和风化碎石层。从土层持水性和导水率来看,枯枝落叶层导水率较大,且有一定持水能力,其持水能力与枯枝落叶干物质有关;均质土壤层导水率相对较小,但土壤持水性相对较大;土石二元混合介质层中,由于土壤含有大量碎石,这些碎石被认为是非透水区,并占据了土壤大量有效孔隙,导致土壤持水性降低,导水率减小。土壤持水性和导水率的减小量与碎石含量及粒径有关;风化碎石层砾石间孔隙较大,导致其导水率极大,而持水性极小;基岩层上广泛分布有裂隙,其中部分裂隙与外界有水量交换,部分无任何水量交换。另外,基岩表面凹凸不平,可以储存部分水量。
1.1.2 模型垂向结构
以等高带为基本计算单元,根据山坡植被、土壤和岩石特性,每个计算单元自上而下可分为4层:植被冠层截留层、地表储留层、土壤层和基岩储留层,其中植被截留层包括高植被截留层(乔木冠层)和矮植被储留层(灌木林地、草地、裸地),地表储留层包括枯枝落叶储留层和洼地储留层,基岩储留层包括基岩凹凸面储留和封闭裂隙储留。计算单元内状态变量包括:植被冠层截留量、洼地储留量、枯枝落叶储留量、土壤含水量、基岩凹凸面及封闭裂隙储留量等,主要参数有植被最大截留深、洼地最大储留深、枯枝落叶干重、土壤饱和导水系数、土壤饱和含水率、土壤田间持水率、湿润锋吸力、土壤厚度、土壤层碎石体积比例系数、基岩凹凸面及封闭裂隙储留深、坡面糙率等。
1.2 模型计算过程
1.2.1 植被截留计算
忽略降雨期间土壤蒸散发,植被截留量的计算公式为
(1)

Wrmax=0.2VegLAI
式中:Veg为植被的面积占计算单元的面积比例,%;Wr表示植被截留水量,mm;Wrmax为最大植被截留水量,mm;P为降雨量,mm;Rr为植被冠层流出水量,即超出最大植被截留水量的部分,mm;LAI为叶面积指数。
1.2.2 洼地储留计算
忽略降雨期间土壤蒸散发,地表储留量采用下式计算:
(2)

式中:Hu2为地表储留深;Hu2max为土壤表层最大储留深;Ru2为土壤表面径流;f为入渗率。
地表储留量由洼地储留量和枯枝落叶储留量构成,枯枝落叶储留量消耗于后期蒸散发过程,而洼地储留消耗于土壤入渗。枯枝落叶储留深Humax采用下式计算:
Humax=ξmaxG
(3)
式中:G为枯枝落叶干质量;ζ为枯枝落叶最大持水系数。
1.2.3 基岩凹凸面及封闭裂隙储留计算
忽略降雨期间土壤蒸散发,基岩凹凸面及封闭裂隙储留计算公式如下:
(4)

式中:Hu1为基岩凹凸面及封闭裂隙储留深;Hu1max为基岩凹凸面最大储留深;Ks为土石介质饱和导水系数;Ru1为基岩表面径流;L为计算单元长度;q为上层土壤下边界水分通量。
降雨期间,基岩面上方下渗水分首先填充基岩凹凸面及封闭裂隙,然后产生基岩面壤中流;非降雨期,基岩凹凸面及封闭裂隙储留主要消耗于植被蒸腾过程。
1.2.4 土壤入渗计算
山坡土壤层较薄(通常为1 m左右),垂向分层方式表现为细(均质土壤)、粗(土石二元介质)和更粗(风化碎石)。土壤入渗初期,土壤含水量较小,土壤入渗以垂向一维入渗为主。随着入渗的进行,当湿润锋接触基岩后,由于基岩裂隙层只有部分裂隙可以导水,大部分基岩层不透水,导致大部分入渗水分聚集在基岩层。聚集的水分首先补给凹凸面及封闭裂隙储留层,当达到最大储留深后,继续入渗的水分将产生侧向壤中流。此时,土壤水分运动由一维为主转变为二维。
降雨期土壤入渗过程采用Green-Ampt模型分层模拟土壤累积入渗量、湿润锋距离随时间变化关系。所述的土壤积水入渗过程计算包括:
湿润锋在第1层时,土壤积水入渗计算式为
(5)
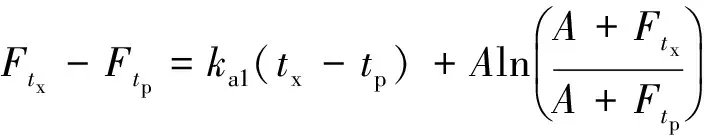
(6)
其中A=SW1Δθ1
Δθ1=θst1-θ0t1
式中:fpt为土壤入渗率;k为土壤饱和导水系数;Ftx为土壤tx时刻累积入渗量;Ftp为积水发生时刻tp土壤累计入渗量;ks1为第1层的饱和导水系数;SW1为第1层中湿润锋处的土壤水吸力;A为参数;Δθ1为第1层土壤含水变化量;θst1为湿润区第1层土石介质饱和含水量,θ0t1为第1层初始土壤含水量。
湿润锋在第m(2≤m≤n)层时,积水入渗计算式为
(7)
Ftx-Fm-1=kam(tx-tm-1)+

(8)
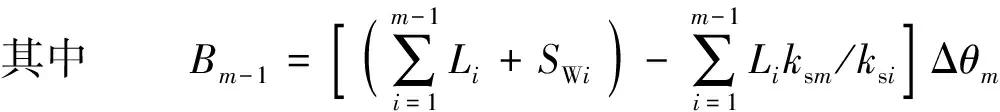
Δθi=θsti-θ0ti
式中:ksm为第m层土壤的饱和导水系数;Bm-1、Cm-1为参数;Fm-1为m-1层以上的土壤累积入渗量;tm-1为湿润锋进入m-1和m层界面时的时间;SWi为第i层中湿润锋处的土壤水吸力;Li为第i层土壤的厚度;θsti为湿润区第i层土石介质饱和含水量;θ0ti为第i层土石介质初始含水量。
在此计算过程中,引入碎石体积比例系数Rv定量描述碎石对各层土壤含水量的影响和土壤饱和导水系数的影响:
θsti=(1-Rv)θsi
(9)
θ0sti=(1-Rv)θ0si
(10)
Ksti=(1-Rv)Ksi
(11)
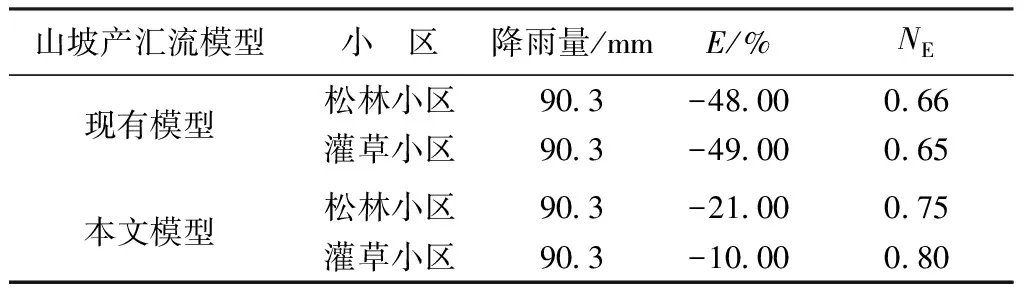
式中:θsi、θsti分别为第i层均质土壤和土石混合介质的饱和含水量;θ0si、θ0sti分别为第i层均质土壤和土石混合介质的初始含水量;Ksi、Ksti分别为第i层均质土壤和土石混合介质饱和导水系数;i为土壤层,i=1代表均质土壤层,此时Rv=0,而i=2、3分别代表土石二元混合介质层和风化碎石层,此时0 1.2.5 壤中流计算 当土壤含水量超过田间持水量后,土壤开始产生壤中流,土壤壤中流采用Darcy定理计算: (12) 式中:q为水流通量;Ks为饱和导水系数,其大小等于壤中流产生层土石介质饱和导水系数;H为土壤水压力水头。 1.2.6 坡面汇流计算 采用运动波方程进行坡面汇流模拟,公式如下: (13) Sf=S0 (14) (15) 式中:Q为断面流量;A为过流断面面积;qL为单宽入流量;Sf为摩擦坡降;S0为计算单元平均地面坡降;R为过流断面水力半径;n为Manning糙率系数。 为充分验证模型模拟效果,选择2个径流小区开展天然降雨产汇流试验,小区内植被分别以人工油松林和荆条为主。其中,人工油松林小区(以下简称松林小区)坡度12°,有油松15株,平均高7.4m,胸径10.4 cm,郁闭度43%。林下有槐树、荆条、酸枣等灌木以及白草、羊胡子草等草本植被,枯落物较少,植被覆盖度在80%以上。次生灌草小区(以下简称灌草小区)坡度18°,坡面植被以荆条为主,高度约为1.5 m,其次还有酸枣等灌木以及白草、羊胡子草等,总覆盖度95%以上。两个小区位于同一山坡,相距大约50 m,坡向,降雨特性,基岩等相同。此外,两小区大小均为5 m×15 m(沿坡向),土层厚度均为20 cm左右,四周用混凝土隔水墙砌至基岩。 表1 土石山坡降雨入渗产流模型中土壤属性参数 径流小区监测了天然降雨过程、土壤含水量动态过程、土壤基质势变化过程及出流过程。在每个径流小区均布置有翻斗式自计雨量计,由HOBO计数器进行实时监测和记录降雨过程;在坡面上下2个断面(各自距径流小区的上、下边界5 m)各选择4个深度(10 cm、20 cm、30 cm、50 cm)埋设土壤湿度传感器(SWR)和负压计,其中SWR的数据为自动采集,而负压计由专人负责每天早晚各读取一次读数。 径流小区坡面下端分坡面流、壤中流两层,分别接入薄壁三角堰箱(堰角30°),并用投入式自计水位计每1 min采集一次堰箱水位。各层的产流量分别用集水桶收集,每次降雨出流后,人工测量每层出流的总量。通过水力学计算推导,可以得出次降雨的径流过程,并与实测值进行比对校正。 正常情况下,取出流结束后的稳定水位为零值水位,先计算水头: h=hi-h0 (16) 式中:h为三角堰出流水头;hi为出流时的实时水位;h0为零值水位。 出流过程采用下式计算: (17) 式中:g为重力加速度;θ为三角堰堰角,其中坡面流的三角堰堰角为30°,壤中流三角堰堰角为20°。 模型采用2009年7月13日次降雨入渗产流过程,模型输入的土壤属性参数见表1。 模型主要参数包括叶面积指数、最大洼地储留深、枯枝落叶量、最大基岩凹凸面及封闭裂隙储留深和碎石含量等。当模型应用于小区、山坡等单元时,由于下垫面条件复杂,空间分布差异很大,导致这些模型参数在研究区各点有较大差别。因此,在模型实际应用时,为确定研究区模型参数,一般通过选择代表性位置开展小区试验进行参数测定,将测定值作为模型参数的参考值,随后根据流域产汇流过程模拟进行率定。其中,代表性位置的选择需要基于对研究区地质地貌特征的全面、整体考察。 在小区试验中,这些参数通过相关仪器和手段可以确定,如叶面积指数可以采用冠层分析仪测定;洼地凹凸面大小可以通过近景摄影测量技术测定;单位面积枯枝落叶量可以通过烘干法测定;基岩凹凸面可以通过开挖剖面,并配以近景摄影测量技术测定。剖面开挖尺度应视基岩类型而定,通过开挖一系列不同尺度的剖面,逐一测定其基岩凹凸面大小,当测定值稳定时的剖面开挖尺度作为试验尺度;封闭裂隙储水量大小可以采用注水法测定;碎石比例可以通过筛分法测定(过2 mm筛)。 研究区洼地储留深均为2.5 mm,枯枝落叶较少,均不予考虑;松林小区和灌草小区冠层最大截留深分别为2.5 mm和1.0 mm,叶面积指数分别为2.5和1.0;基岩凹凸面及封闭裂隙总储留深均为10 mm,初始水量为2 mm。 模型模拟输出为地表径流强度和土壤入渗率,结合松林小区和灌草小区降雨产汇流试验结果,采用模拟值与实测值间的相对误差E和Nash-Sutcliffe效率系数NE对模型模拟结果进行评价。计算公式如下: (18) (19) 2.3.1 地表径流强度模拟结果分析 针对现有山坡降雨入渗产流模型和本文构建的模型(以下简称本文模型),松林小区和灌草小区降雨产汇流试验得到的地表径流强度实测值与两模型模拟值间的相对误差与Nash-Sutcliffe效率系数见表2。从表2可知,本文模型模拟效果得到了较大提高,松林小区E由-48%升至-21%,NE由0.66升至0.75;灌草小区E由-49%升至-10%,NE由0.65升至0.80。可见本文模型模拟的地表径流过程与实测过程比较吻合(图1),能够用于估计土石山区山坡地表径流强度。 表2 地表径流强度模拟误差分析 图1 地表径流强度实测与模拟过程 2.3.2 土壤入渗率模拟结果分析 两个小区的土壤入渗率模拟情况如表3所示。从表3可知,相对于现有模型,本文模型模拟效果有明显提高,松林小区E由42%降至25%,NE由0.66升至0.75;灌草小区E由33%降至28%,NE由0.44升至0.75。进一步对比土壤入渗率实测与模拟过程(图2)发现,在雨强较小时(≤2.0 mm/min),本文模型模拟值与实测值吻合较好,而在强降雨期(>2.0 mm/min)模型模拟值明显小于实测值,模拟效果较差。根据观测结果,土壤入渗率在暴雨期会出现较大幅度的提高,模拟值却变化很小。究其原因,可能是因为土石山区山坡土壤中碎石的存在使得碎石与土壤的直接接触面形成水流快速通道,在暴雨期水分可以通过优先流迅速入渗,土壤入渗率迅速增大,而本文模型中并未考虑优先流所带来的影响,导致土壤入渗率模拟结果出现较大程度的失真。未来在进行土石山区山坡降雨产汇流过程模拟时,需要充分考虑土壤层和基岩层中优先流的存在。现有模型尚未考虑碎石含量对入渗过程影响,导致模型计算较高估计了土壤入渗强度,较小估计了地表产流量(径流强度)。同时,现有模型也未考虑优先流对入渗过程影响。两者共同作用下,导致现有模型模拟失真更加严重。 表3 土壤入渗率模拟误差分析 图2 土壤入渗率实测与模拟过程 基于对土石山区下垫面特性的分析,引入碎石体积比例系数Rv量化土壤中碎石的存在对山坡土壤水分运动的影响,并考虑了基岩凹凸面及封闭裂隙储留,进而构建了一种土石山区坡地降雨入渗产流模型。由于山坡单元下垫面条件复杂,空间差异较大,模型具体应用时无法直接测定反映研究区实际的模型参数值,需要选择典型区开展小区径流试验进行测定,并通过流域产汇流过程模拟最终确定。本文选择松林小区和灌草小区两种径流小区开展天然降雨产汇流试验,分别利用现有山坡降雨入渗产流模型和本文模型模拟计算地表径流强度和土壤入渗率,通过对比分析验证模型改进后的适用性和可靠性。 本文模型对地表径流强度和土壤入渗率的模拟效果较好,但在暴雨期内土壤入渗率模拟结果要远小于实测值,模拟效果较差。可能原因在于土石山区山坡土壤中碎石的存在造成碎石与土壤的直接接触面可能存在水流快速通道,暴雨期水分通过优先流通道迅速下渗,导致土壤入渗率迅速增大,而本文构建模型时未考虑优先流的存在,导致模拟出现较大程度的失真。因此,本文模型还有待进一步完善,未来需要充分考虑优先流的存在对土石山区山坡入渗产流过程的影响。本文研究丰富了土石山区山坡土壤水分运动的理论,为土石山区水循环过程模拟提供了参考,也为下一步开展两流区(基质区和优先流区)模型研究奠定了基础。 [1] 芮孝芳,梁霄.水文学的现状及未来[J].水利水电科技进展,2011,31(2):1-4.(RUI Xiaofang,LIANG Xiao.Present situation and future of hydrology[J].Advances in Science and Technology of Water Resources,2011,31(2):1-4. (in Chinese)) [2] 芮孝芳,刘方贵,邢贞相.水文学的发展及其面临的若干前沿科学问题[J].水利水电科技进展,2007,27(1):75-79. (RUI Xiaofang,LIU Fanggui,XING Zhenxiang.Advances in hydrology and some frontier problems[J].Advances in Science and Technology of Water Resources, 2007,27(1): 75-79. ( in Chinese)) [3] PHILIP J R. Hillslope infiltration: planar slopes[J]. Water Resources Research, 1991, 27(1): 109-117. [4] TROCH P A, PANICONI C, VAN LOON E. Hillslope-storage Boussinesq Model for subsurface flow and variable source areas along complex hillslopes: 1. Formulation and characteristic response[J]. Water Resources Research, 2003, 39(11):177. [5] HILBERTS A G J, TROCH P A, PANICONI C, et al. Low-dimensional modeling of hillslope subsurface flow: relationship between rainfall, recharge, and unsaturated storage dynamics[J]. Water Resources Research, 2007, 43(3):305-310. [6] CHEN L, YOUNG M H. Green-Ampt infiltration model for sloping surfaces[J]. Water Resources Research, 2006, 42(7): 887-896. [7] HOPP L, MCDONNELL J J. Connectivity at the hillslope scale: identifying interactions between storm size, bedrock permeability, slope angle and soil depth[J]. Journal of Hydrology, 2009, 376(3): 378-391. [8] LIAO K H, LÜ L G, YANG G S, et al. Sensitivity of simulated hillslope subsurface flow to rainfall patterns, soil texture and land use[J]. Soil Use and Management, 2016, 32(3): 422-432. [9] 胡堃,于静洁,夏军,等.华北石质山区坡地产流模型[J].地理研究,2006,25(4):673-680. (HU Kun, YU Jingjie, XIA Jun, et al. Plot-scale runoff generation model of lithoid mountainous areas in North China[J]. Geographical Research, 2006, 25(4): 673-680. (in Chinese)) [10] 穆天亮,王全九,王辉.黄土坡面定雨强入渗产流物理基础模型研究[J].西北农林科技大学学报(自然科学版),2009,37(10):199-203. (MU Tianliang, WANG Quanjiu, WANG Hui. Study on physical base model of infiltration and runoff formation on loess slope land for a fixed rainfall intensity during rainfall[J]. Journal of Northwest A & F University (Natural Science Edition), 2009, 37(10): 199-203. (in Chinese)) [11] 刘贤赵,康绍忠.黄土区坡地降雨入渗产流中的滞后机制及其模型研究[J].农业工程学报,1999,15(4):95-99. (LIU Xianzhao, KANG Shaozhong. Hystersis mechanism and model of rainfall-Infiltration-runoff on hillslope in loess area[J]. Transactions of the CSAE, 1999, 15(4): 95-99. (in Chinese)) [12] 陶汪海,吴军虎. 坡地产流产沙规律数值模拟研究[J]. 水土保持学报,2016,30(1):54-57. (TAO Wanghai, WU Junhu. Study on numerical simulation of slop runoff and sediment yield rule[J]. Journal of Soil and Water Conservation, 2016, 30(1): 54-57. (in Chinese)) [13] 刘昌明,李军,王中根.水循环综合模拟系统的降雨产流模型研究[J].河海大学学报(自然科学版),2015,43(5):377-383.(LIU Changming,LI Jun,WANG Zhonggen.Study on rainfall-runoff model of hydro-informatic modeling system[J].Journal of Hohai University (Natural Sciences),2015,43(5): 377-383.(in Chinese))
2 模型验证
2.1 径流小区天然降雨产汇流试验

2.2 模型参数
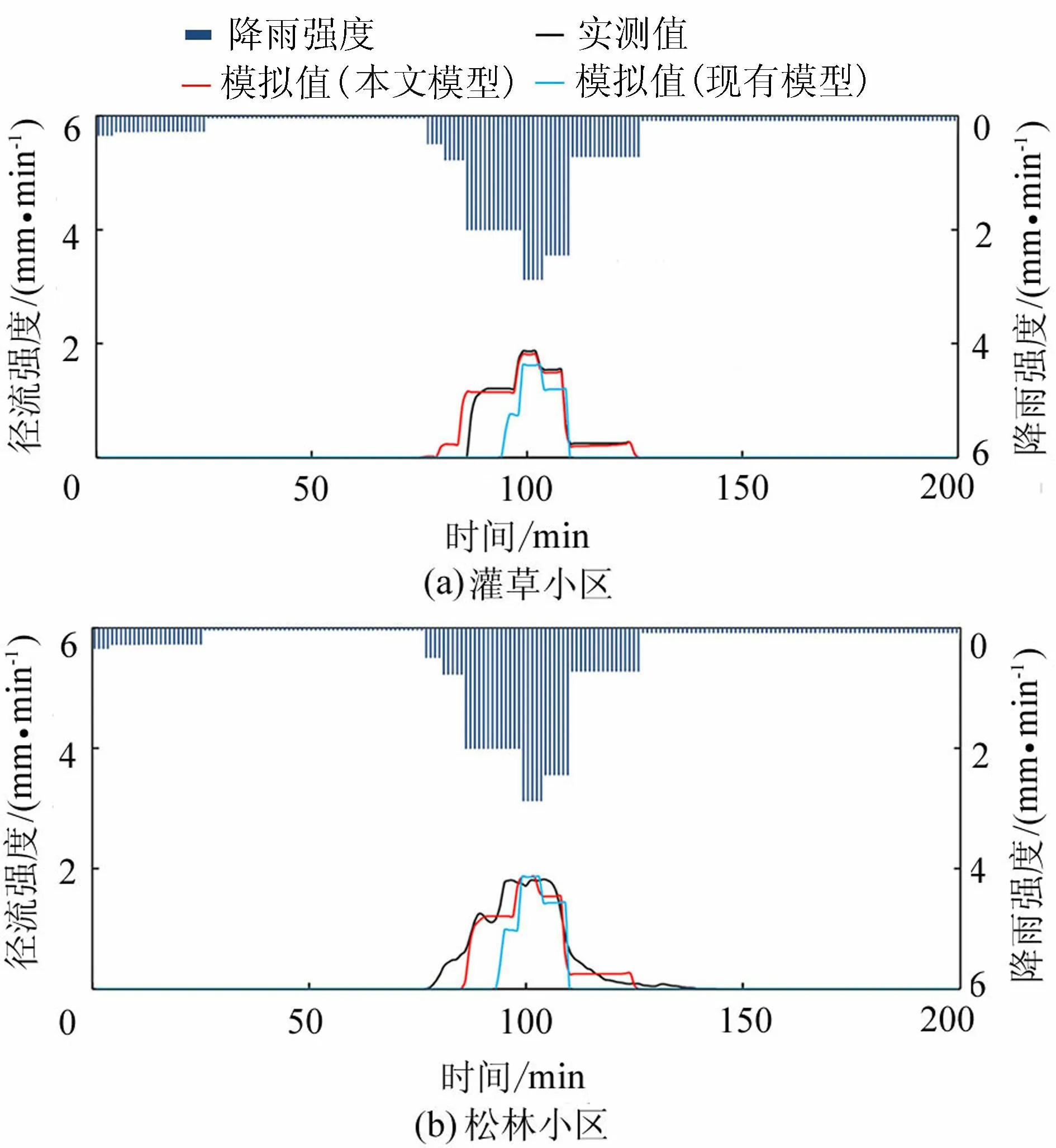
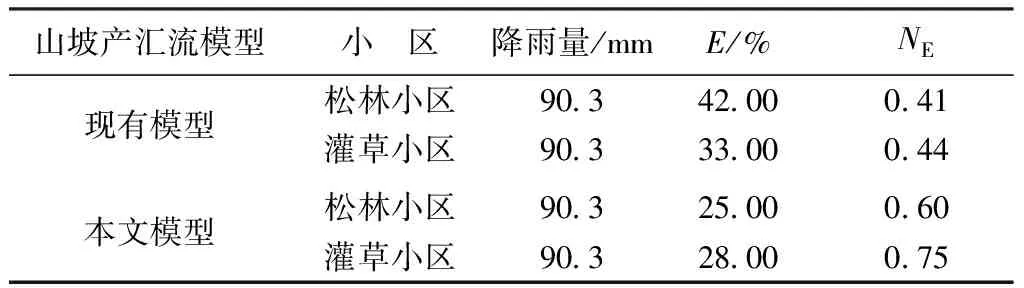
2.3 模型模拟结果分析


3 结 语

