一种时-频分析算法识别Scholte波算法研究

2018-03-06 02:55张自圃邵雨新

沈阳理工大学学报 2018年1期

李环，张自圃，邵雨新，吴强

(沈阳理工大学信息科学与工程学院，沈阳 110159)

在浅海海域，舰船在航行时产生的舰船噪声会以波的形式向各个方向传播，其中有一部分会以低频波的形式传到海底，产生海底地震波[1]。海底地震波沿着流-固界面向远处传播时形成Scholte波[2]，Scholte波的传播特性使得对其识别很重要。

Scholte波的特点是在沿着海底流-固界面传播时衰减很慢，质点的振幅在垂直分界面方向上随离开流-固界面距离的增大呈指数衰减，主要能量集中在半波长深度内。质点的极化运动轨迹是在水平方向和垂直方向组成的平面内做椭圆运动，没有低频截止频率。Scholte波还具有到达时间最晚、频率低、幅值居中、能量最大、能量主要集中在5～80Hz之间等特点。

本文根据Scholte波的特性，提出了一种新算法识别Scholte波。

1 匹配追踪与魏格纳分布联合算法识别Scholte波

1.1 匹配追踪的基本原理[3]

在信号处理时，匹配追踪虽然与正交分解很相似，但用来分解信号库内的基本函数不一定是正交的。

首先，建立一个基本函数库D，然后用库中的函数分解信号的波形。对于库函数，并不要求库中的所有基本函数gi(t)互相正交，但要求其范数 ‖gi(t)‖=1。因为基本函数不相互正交，所以，不相互独立，即有冗余。现在用函数库D里的一组函数gi(t)(i=1,2,3,…)的线性组合来表示待分解信号f(t)。

先从库里选出与给定函数最匹配的g0(t)，即内积〈f(t),g0(t)〉是所有D内成员与f(t)内集中最大的一个。

〈f(t),g0(t)〉>〈f(t),gi(t)〉,i≠0,g0(t)∈D

(1)

f(t)可分解成

f(t)=〈f(t),g0(t)〉g0(t)+Rf(t)

(2)

式中Rf(t)是第一次匹配后的残余。因为Rf(t)必定与g0(t)正交，所以有

‖f(t)‖2=|〈f(t),g0(t)〉|2+‖Rf(t)‖2

(3)

再对Rf(t)作类似匹配：从D中再选出对Rf(t)最匹配的另一个基本函数g1(t)，于是有

Rf(t)=〈Rf(t),g1(t)〉g1(t)+R2f(t)

(4)

‖Rf(t)‖2=|〈Rf(t),g1(t)〉|2+‖R2f(t)‖2

(5)

式中R2f(t)是第二次匹配后的残余。

对信号f(t)的分解过程是把信号垂直投影到基本库函数D的元素上进行重复迭代估算，如图1所示。

对残余部分重复以上步骤,第n次匹配后有

Rnf(t)=〈Rnf(t),gn(t)〉gn(t)+Rn+1f(t)

(6)

及

‖Rnf(t)‖2=|〈Rnf(t),gn(t)〉|2+‖Rn+1f(t)‖2

(7)

把N次匹配结果依次回代便可得分解公式：

(8)

及能量守恒：

‖RNf(t)‖2

(9)

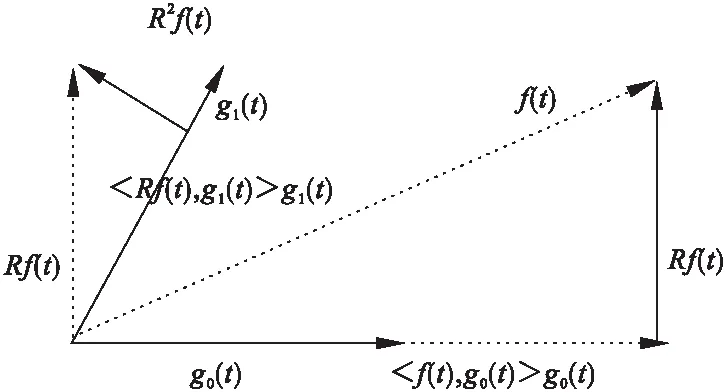
图1 信号分解示意图

1.2 魏格纳分布[4]

信号s(t)的魏格纳分布是

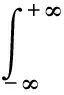
(10)

由其频谱可表示为

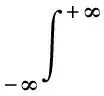
(11)

对于信号s(t)来说，在时间域的自相关可以表示为

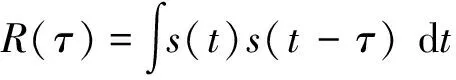
(12)

信号s(t)的傅里叶变换是S(ω)，则功率谱可表示为

(13)

因为S(ω)是s(t)的线性函数，而P(ω)又是S(ω)的二次函数，所以，对于魏格纳分布的定义可以理解为是从功率谱得到的分布即被称为双线性(二次)时-频分布。

另一方面，阿斯科尔尼科夫在杀人之后受到心灵的拷问，他十多次提及是有魔鬼在引诱他，并不是他杀人，而是魔鬼。这恰恰与圣经中引诱亚当偷吃禁果的蛇、圣经中的撒旦相一致。后来的许多文学作品中或多或少的涉及到这种引诱者形象。就是在“魔鬼”的引诱下，阿斯科尔尼科夫把杀害阿谬娜的事当做对现实社会的探讨。不管是从阿斯科尔尼科夫杀人来看，还是从魔鬼引诱他犯罪这都和《圣经》中的撒旦、托马斯曼的浮士德博士的恶魔引诱同源。

1.3 匹配追踪与魏格纳分布联合算法

由于魏格纳分布在时-频域有很好的分辨率，便于观察信号的时间、频率、能量等信息。当分析包含有多分量的信号时却又引入了影响分析的交叉项。之后研究者提出了许多抑制交叉项的方法，例如：平滑魏格纳分布、平滑伪魏格纳分布。但在这些方法中，有的以牺牲时-频域的分辨率为代价，有的破坏了魏格纳分布的一些特性。

基于以上考虑，希望保留魏格纳分布的优良特性，又不想引入交叉项。所以利用匹配追踪算法能够分解与重构信号的特点，把含有多分量的信号分解，即公式(8)。

对式(8)分解所得的每一项〈Rnf(t),gn(t)〉gn(t)做魏格纳分布，再把每一项魏格纳分布的结果加在一起，这样既保留魏格纳分布的优良特性，又避免了交叉项的引入。但由于匹配追踪算法需要较长时间来分解与重构信号，故这种方法也需要较长的时间。

对信号做匹配追踪分解信号和对重构信号做魏格纳分布，具体的实现过程如下。

(1)由于Gabor型时-频原子与时间域和频率域都是相关联的，且所选用的参数都是可控的，调整起来比较灵活。所以选用这种原子作为基本函数原子。

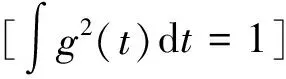
(14)

则定义Gabor型时-频原子如下

(15)

相应的频域表示为

(16)

式中：τn为位移变量；an为尺度变量；ejωnt为调制作用；通常把参数[an,τn,ωn]记作γn，则gan,τn,ωn(t)简记为gγn(t)。

(2)把构造的基本函数库D中的元素按照下述原则从t-ω平面的离散栅格上抽取，令Δτ、Δω分别是栅格在时间、频率两个坐标轴上的间距，且

(17)

再令a0>1为基本尺度因子，并按

(18)

的关系从离散栅格上取γ相对应的元素gγ(t)。

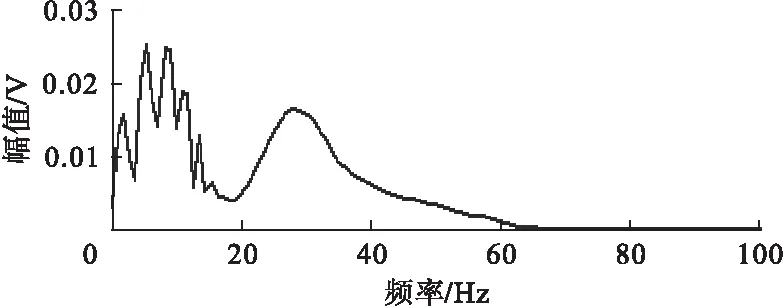
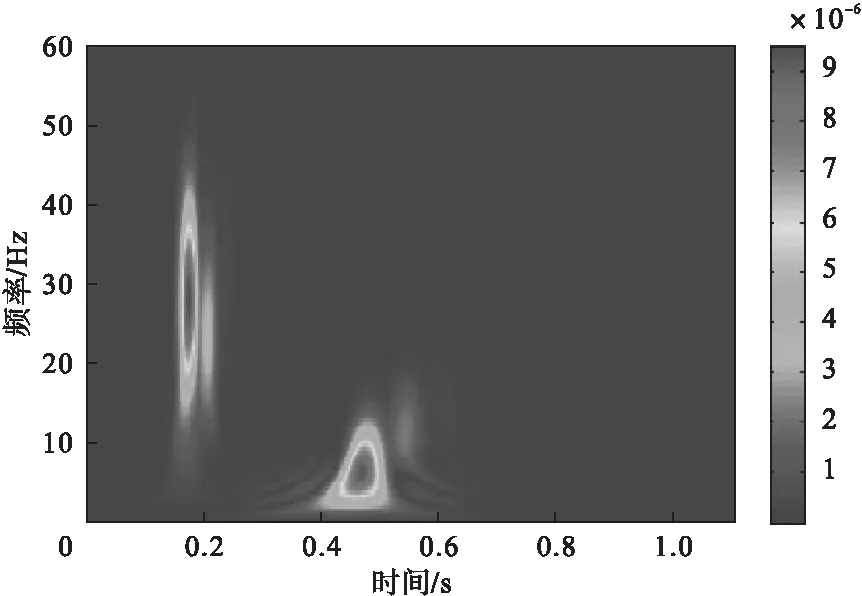
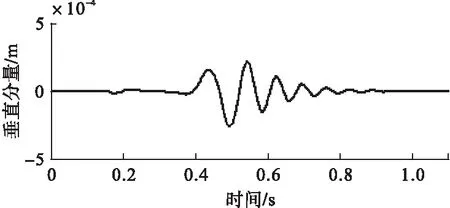
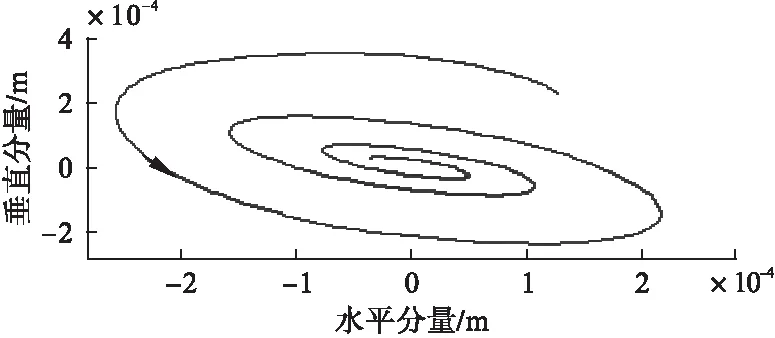
对于一个长度为N的目标信号，通常取a0=2,Δτ=1/2,Δω=π/6,0

匹配追踪与魏格纳分布联合算法对魏格纳分布算法有了很大的改进，有效的抑制了交叉项的干扰，不同于伪魏格纳分布和平滑伪魏格纳分布那样需要牺牲时间域或频率域的分辨率来抑制交叉项，对处理含有较少波存在的信号比较适用。

2 地震波的极化及Scholte波的质点运动轨迹

极化滤波是基于波的偏振特性的空间滤波方法，是波偏振研究和多波资料解释的基本工作之一[5]。

地震波极化的方法对以不同形式偏振(波通过空间记录点时介质质点的位移矢量末端绘出的轨迹)和不同方向传播的波比较适用，这种方法能够得到介质振动的详细信息[6]，在地震勘探和对地震数据处理的过程中有着重要的作用，能够帮助处理地震信号中的信息并了解地质成分构成，还能根据横波、纵波及面波的不同极化特性实现对其识别及分离。

地震时，质点沿一定的方向和形状来振动，继而产生一定的运动轨迹。不同的波产生的运动轨迹不同，可以利用不同的运动轨迹来区分不同的波。

横波、纵波、Scholte波质点的运动轨迹：

(1)横波是线性偏振波，即质点在围绕平衡位置的振动轨迹是直线段。在均匀介质中，质点的振动矢量在横波与纵波波前相切的平面内与射线方向垂直，极化的轨迹为一条直线段。

(2)纵波也是线性偏振波，即质点在围绕平衡位置的振动轨迹也是直线段，但是它的振动轨迹与横波不同，其质点位移方向与其传播的方向相同，所以极化后的轨迹是很多条直线段。

(3)Scholte波的质点振动轨迹和瑞雷面波相似，都是椭圆偏振波，在水平方向和垂直方向构成平面内的极化轨迹是椭圆形。

实际地震勘探时，介质往往是不均匀的，所以形成的波场不像在均匀介质中那样每种波都容易被区分开，而是由很多种类别的波相叠加构成。

本文应用极化滤波的方法主要是为了区分和识别Scholte波，而Scholte波在水平分量和垂直分量上的极化图形是椭圆形。故在此使用二分量地震记录来对不同性质的波和不同类别的波进行区分。

3 识别Scholte波

现用传感器接收距离震源300m处的水平分量地震波形(如图2)，对水平分量做傅里叶变换，水平分量的频谱图如图3所示。对水平分量魏格纳分布得到的时频图如图4所示，从图4中能够看到魏格纳分布的时频分辨率很高，图形清晰，但却引入了图中0.3～0.4s位置的交叉项，影响了时频分布的准确性。

图2 地震信号的水平分量

图3 地震信号水平分量的频谱图

图4 地震信号水平分量的魏格纳分布

对地震信号的水平分量用匹配追踪的方法进行分解和重构，当对信号进行100次重构后，信号的残差幅值在1×10-6以下，认为信号已基本完成重构。重构信号如图5所示，残差信号如图6所示。

图5 地震信号水平分量第100次重构图形

图6 地震信号水平分量第100次重构的残差图形

对分解后的信号做魏格纳分布，得到重构信号的魏格纳分布如图7所示。新算法要对目标信号进行多次分解与重构，需要花费时间，图7是进行了100次重构得到的完整时-频分布。把图7与图4比较，图7和图4一样清晰，且抑制了图4中交叉项部分。所以，新算法相比于魏格纳分布有很大提高。本次运算中魏格纳分布用了1min，新的算法费时较长用了30min，这是这种算法的缺点。