物理考试命题数据自洽分析——以导体棒切割磁感线运动为例

吴广国 黄琭琰 邹 斌

(1. 北京景山学校,北京 100006; 2. 中央民族大学理学院,北京 100081)

导体棒(导体框的一部分)在磁场中切割磁感线而形成感应电流时,由于导体棒(导体框)受到安培力而减速运动,由于导体棒(导体框)所受安培力的大小正比于它的速度,所以它做的是加速度逐渐减小的减速运动.[1]导体棒(导体框)速度的严格求解是随时间减小的指数函数,一旦其受力条件和边界条件是确定的,则其运动是唯一确定的.[2]因此,在高考题以及各类模拟题中,虽然命题对象是中学生,不要求严格求解速度和位置的表达式,但题目所给出的都应该是经过严格求解后的数据,不能为了计算方便而随意设置数据.[3, 4]下面以一道某地2018年模拟题为例,进行详细讨论分析.

图1 金属导轨示意图

如图1所示,间距为L=1m的两条足够长的平行金属导轨与水平面的夹角为θ=37°,底端用电阻为R=0.8Ω的导体MN相连接,导轨电阻忽略不计.磁感应强度为B=1T的匀强磁场与导轨平面垂直,磁场区域上下边界距离为d=0.85m,下边界aa′和导轨底端相距为3d.一根质量为m=1kg、电阻为r=0.2Ω的导体棒放在导轨底端,与导轨垂直且接触良好,并以初速度v0=10m/s沿斜面向上运动,到达磁场上边界bb′时,恰好速度为0.已知导轨与棒之间的动摩擦因数为μ=0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.求:

(1) 导体棒通过磁场过程中产生的焦耳热.

(2) 导体棒从进入磁场到达上边界所用的时间和回路中产生的感应电流的有效值.

(3) 微观上导体中的电子克服因碰撞产生的阻力做功,宏观上表现为产生焦耳热.试从微观角度推导:当棒运动到磁场中某一位置时(感应电流为I),其电阻的发热功率为P热=I2r(推导过程用字母表示).

在此我们不对题目进行解答,而只关注导体棒进入磁场后的运动情况.

设导体棒从最低点运动到aa′,进入磁场时速度为v1,由动能定理得

(1)

解得v1=7m/s.

要求导体棒进入磁场后的运动情况,假设磁场足够大,从进入磁场时开始计时(t=0),以磁场边界aa′为坐标原点,建立沿导轨向上的坐标轴Ox,如图2所示,设任意时刻t导体棒速度为v.

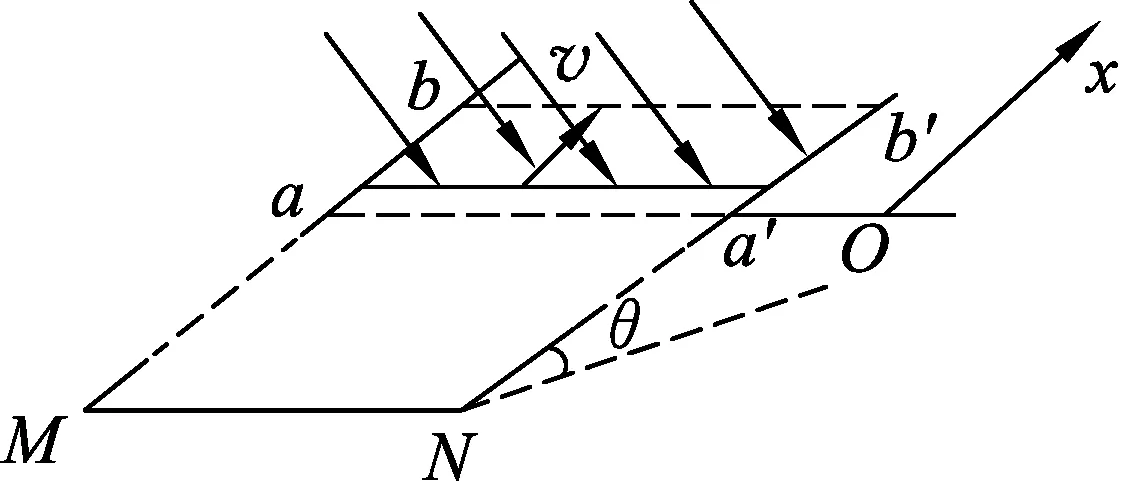
图2 导体棒进入磁场后的运动情况

(2)

代入数据后

(3)

利用初始条件t=0,v=7m/s得到该微分方程的解为

v(t)=17e-t-10. (SI)

(4)

继续利用导体棒位置与其速度的表达式

(5)

并考虑到初始条件t=0,x=0,可以进一步得到在磁场区域内导体棒位置函数

x(t)=-17e-t-10t+17. (SI)

(6)

假设磁场在aa′以上足够大空间存在.由(4)式和(6)式很容易计算出当导体棒速度减小到0时,所需要的时间为t1=ln1.7,此时的位置为x(t1)=1.7m.

即通过解导体棒运动的微分方程可以严格计算出导体棒进入磁场后减速到0时,磁场宽度至少应为1.7m,而非题干所给出的d=0.85m.

利用(5)式和(6)式,我们也可以计算在现有各参数不变的情况下,当导体棒到达磁场上边界bb′时(即d=0.85m),从下边界aa′导体棒运动到上边界的时间约为0.146s,此时导体棒的速度为4.69m/s,导体棒的速度并不为0.通过以上的数据分析和严格的数值求解,命题者认为导体棒在磁场中沿导轨向上运动d=0.85m以后速度为0是不恰当的,题目数据可以修改磁感应强度B的大小也可以通过增加磁场宽度,来达到导体棒恰好通过磁场区域时,速度为0.这种运动速度或者位置函数为指数函数相对较为复杂的运动形式,命题时需要预判位移、速度和时间的数值关系式,避免出现题目数据的不自洽.