基于面板Logistic增长模型中国城镇化演进特征与趋势分析

刘洪涛，尚 进，蒲学吉

（西北工业大学管理学院，西安 710072）

一、引言

城镇化伴随工业化与现代化进程发展，是社会发展的长远方向和必然趋势。而当今世界上主要的工业大国已经基本上完成了城镇化进程，少数国家甚或已出现逆城镇化的情形。自改革开放以来，中国城镇化发展迅猛。1978年以来，中国城镇化快速发展，但改革开放初期发展较为粗放，这一阶段国家开始逐渐减少对农村劳动力转移至城镇的限制；1996年起，中国城镇化逐渐进入加速发展阶段，至2004年以后，城镇中基础设施等投资增大，城镇化发展水平亦显著提升。可见，伴随城镇化发展，城镇建设不断扩张，投资力度亦持续增强。城镇化作为支撑国家经济增长和社会发展的重要引擎受到广泛重视，党的十八大报告亦指出要加快推进中国城镇化进程，深入开展以人为本的新型城镇化。明确中国当前城镇化状况并据此预测城镇化未来发展方向，将有利于认清当前发展形势并深刻理解党中央相关政策，进而促进中国城镇化健康持续发展。

二、文献综述

Northam（1979）研究表明城镇化的增长过程一般呈现一条“S”型曲线的增长规律，且包含三个阶段：起始期（Initial stage），城镇化率低且增长速度较为缓慢；加速期（Acceleration stage），城镇化率增长速度较快；末尾期（Terminal stage），城镇化率高但增长速度逐渐降低且城镇化率增长趋于平缓，该研究为Logistic增长模型的发展和城镇化率演进规律的预测奠定了基础[1]。王远飞和张超（1997）探讨了用Logistic模型来描述城市化过程的合理性，预测了中国城市化率的发展趋势[2]。乔松珊和孙成金（2016）依据城乡人口增长率的变化特点建立优化的Logistic模型并进行实证分析[3]。此外，亦有相关学者将改进的Logistic增长模型运用于省域或县域数据以分析城镇化发展状况[4][5]。上述文献对Logistic增长模型进行优化，均站在整体角度对研究对象城镇化演进状况进行分析。

陈彦光和周一星（2005），冯年华（2005）修正了诺瑟姆曲线，得到一个四阶段的划分结果并进行地理空间解释，进而对中国城镇化进程进行预测[6][7]。王建军（2009）运用高等数学方法，推出城镇化Logistic模型关于时间变量t的方程表达式，并推导出曲线的三个特征点及其数学表达式[8]。陈素平（2015）等采用回归分析方法对城镇化发展各阶段特征点进行探索[9]。张乐勤和张勇（2015）通过Logistic模型分析了中国城镇化快速演进期的时长及增长速度[10]。上述文献将Logistic增长模型划分为若干阶段，描述了各阶段的城镇化研究特征，有利于了解中国城镇化发展进程各阶段的发展动向以及当前发展态势，为中国城镇化下一阶段发展方向、发展速度提供参考。

前人在研究过程中大都通过直接测算整体城镇化水平来考量研究对象的城镇化进程，或者简单依照自然地理状况，将中国各省市分成东部、中部、西部三个地区。直接采用整体城镇化水平笼统地分析中国城镇化的发展进程会将高杠杆值（省份）包含于其中，产生以偏概全的状况；简单分类后再分析所得到的结论亦显粗放，这些均不利于对全国总体形势的认识。本文试图将全国30个省、直辖市、自治区分组，通过面板数据聚类分析，根据城镇化率特征重新构造距离函数并以此衡量各省市的相似性，进而建立面板数据Logistic增长模型，分别对各组的城镇化发展状况进行分析，排除高杠杆值（省份），减小了其对全国城镇化率可能产生的影响，兼顾了各地区城镇化进程的特殊性与一般性，使对城镇化率的测度方法更系统化、客观化。并据此探索中国城镇化发展的特征点，预测城镇化发展方向，以达到全面了解中国城镇化发展态势的目的，为把握当前城镇化发展形势，明确中国城镇化所处阶段，制定未来城镇化战略性指导政策提供科学理论依据。

三、研究方法与数据来源

（一）面板数据的聚类分析

Bonzo（2002）定义聚类标准时以概率连接函数代替传统的距离函数，将聚类过程作为优化问题处理[11]。Ren（2009）基于Fisher次序集群理论，通过Frobenius准则重建了Ward函数提出多变量面板数据序聚类方法[12]。李因果和何晓群（2010）基于上述研究，提出在对面板数据进行聚类分析时需要考虑：（1）各样本指标间的静态距离；（2）时间序列的动态发展特征距离[13]。其综合考量了面板数据“绝对指标”，“增量指标”及“时序波动”等特征，重新构建面板数据相似性测度的距离函数，并通过Ward聚类算法计算类与类之间的距离，以此为基础提出面板数据聚类分析方法。本文沿用其思想，仍采用欧式距离计算面板数据相似性指标的距离测度。鉴于本文采用了单指标面板数据，无法考虑“时序波动”因素，又考虑到城镇化率的演变过程中应受到政策等推动因素的影响，故本文加入了加速度欧氏距离指标，以更好的描绘城镇化发展过程中推动力的作用效果。在聚类分析中综合考虑了城镇化发展的历史与现状、经济和政治等因素，使可以更完善地描绘城镇化率的演变过程，以更好地实现聚类，则根据指标特征重新定义距离测度公式如下。

对面板数据中各数值用双下标变量表示，即xi,t,i=1,2,…,N,t=1,2,…,T，表示第i个个体中t时间的数据，其中N表示面板数据包含的个体数；T表示各横截面时间序列最大值。

定义1 个体间“直接欧氏距离”（Direct Eu⁃clidean Distance），可记为di,j(DED)

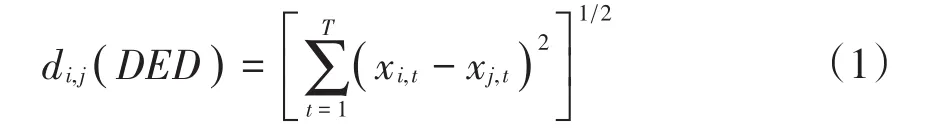
di,j(DED)描绘了整个时间测量范围内个体间数值上距离的远近，在本文中表示对i省份与j省份城镇化率的差异（历史和发展现状因素差异）测度。

定义2 个体间“速度欧氏距离”（Speed Eu⁃clidean Distance），可记为di,j(SED)

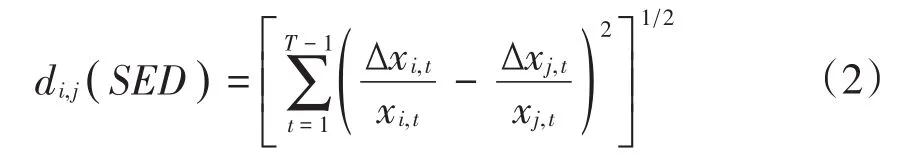
其中 ∆xi,t=xi,t+1-xi,t，∆xj,t=xj,t+1-xj,t。∆xi,t，∆xj,t表示相邻时期个体的绝对值差异。di,j( )SED描绘了整个时间测量范围内随时间变化个体间速度的差异，在本文中表示对i省份与j省份城镇化率增长速度的差异（经济因素差异）测度。

定义3 个体间“加速度欧氏距离”（Accelerat⁃ed Speed Euclidean Distance），可记为di,j(ASED)

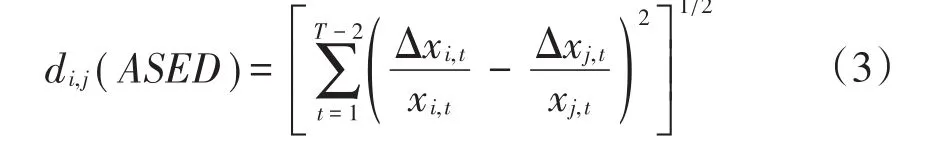
定义4 个体间“综合加权欧式距离”（Com⁃prehensive Weighted Euclidean Distance），可记为di,j(CWED)

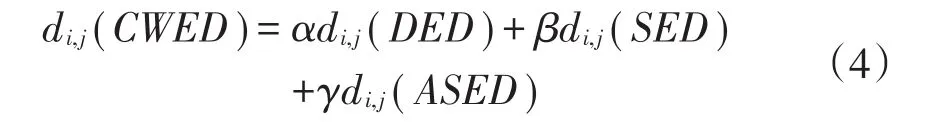
其中，α+β+γ=1，α、β、γ代表相应距离的权重系数。综合加权欧式距离中权重系数可以通过实际问题进行主观判定或者客观判定，常用方法如专家评分法、层次分析法、模糊判别法等。通过观察上式可知，若β=γ=0，则综合加权欧式距离等同于直接欧式距离，即传统欧式距离测度。

本文采用系统聚类法中的Ward法，其基本思想为方差分析，若分类得当则同类样本间的离差平方和最小，不同类样本间离差平方和相对较大。

（二）面板数据的Logistic增长模型

韩本毅（2011）在研究中表明中国城镇化进程从1978年之后逐步体现Logistic曲线的特征，此后众多学者亦采取类似方法对不同范围的城镇化演进过程进行探索[14]。对此，本文亦采用Logistic模型考察中国城镇化进程的发展规律，但又依据聚类分析结果将全国30个省、直辖市、自治区分成M类，选取每一类数据的重心值形成一个横截面，建立M个横截面T时期的面板Logistic模型。

传统的Logistic模型表达式为：

其中：U代表城镇化水平，UMax代表城镇化水平的上限，a代表积分常数，b代表增长系数，t代表时间，t=1,2,…,T。为使便捷地确定回归模型的参数，令a=lnUMax·c，b=-lnd，即：

其中：c代表模型回归常数，d代表回归系数。

本文基于上式，将其扩展为面板模型如下：

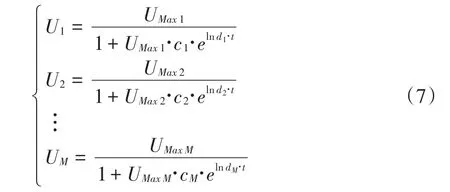
其中：Ui代表第i个横截面的城镇化水平，ci代表第i个横截面的模型回归常数，di代表第i个横截面的回归系数，UMaxi代表第i个横截面的城镇化水平上限。为方便进行拟合，可将上述模型线性化后再进行回归。

（三）Logistic增长模型的阶段划分以及分界点测量

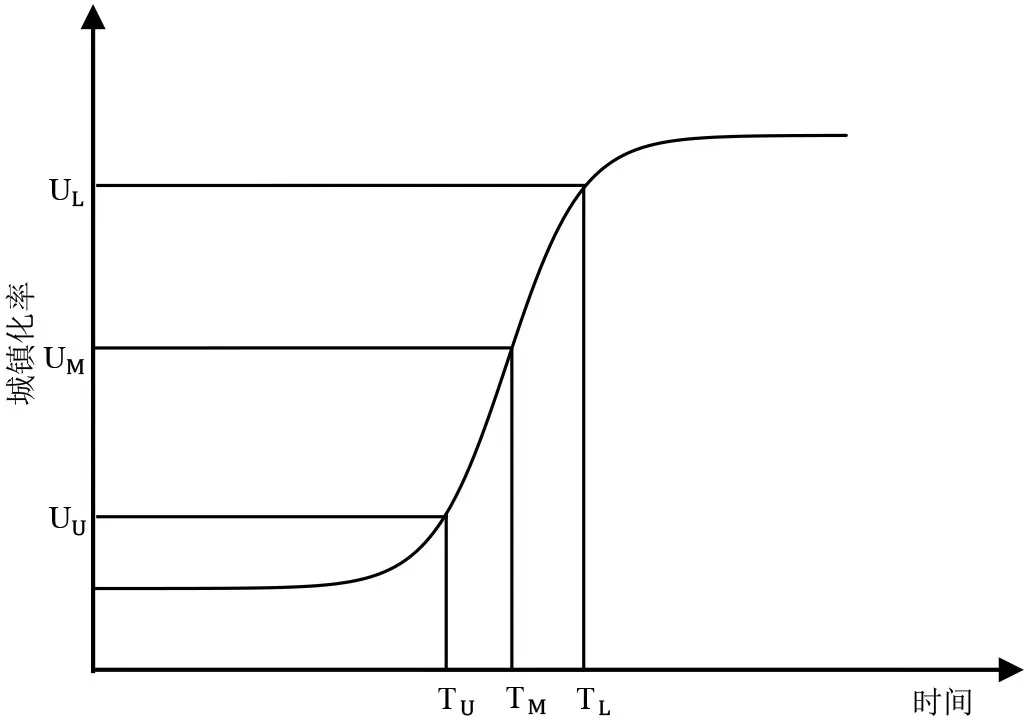
图1 Logistic增长模型示意图

Logistic增长模型的总体趋势可直观地表示如图1。

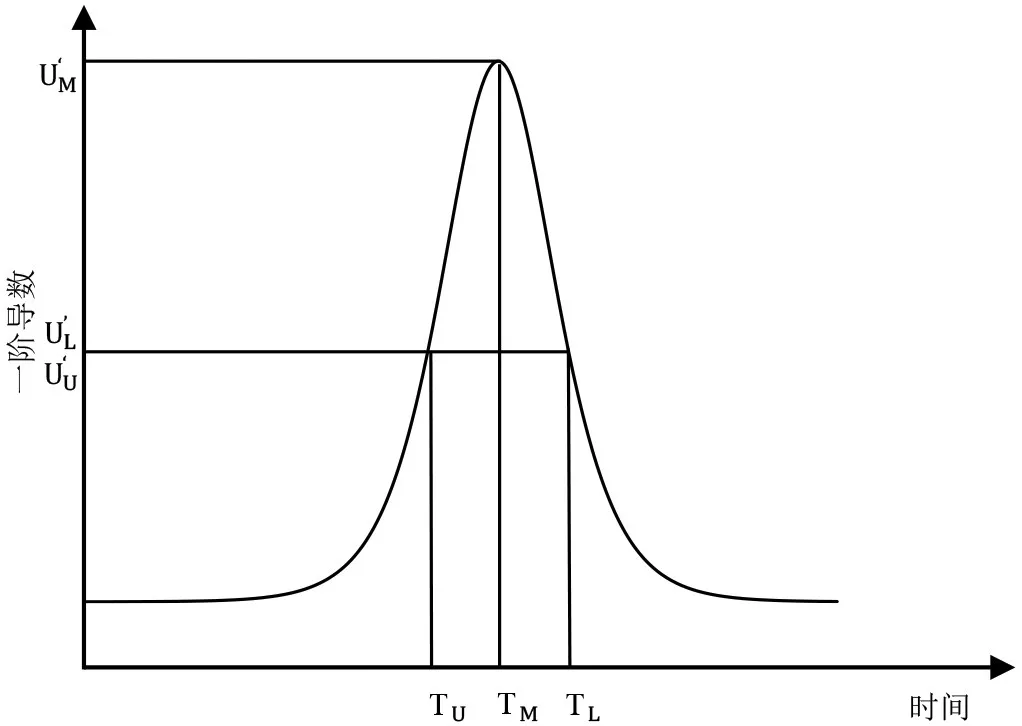
图2 Logistic增长模型一阶导数示意图

同样地，亦可依据图1作出Logistic增长模型导数及二阶导数图像如图2、图3。

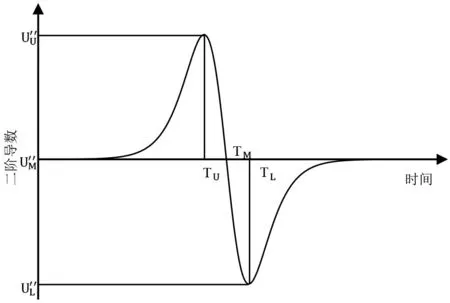
图3 Logistic增长模型二阶导数示意图

本文依据图2、图3可在图1中找到三点(TM,UM)，(TU,UU)，(TL,UL)。并可依据三点将城镇化发展的整体进程划分为三个阶段，找到城镇化发展速度最快的时期。其中，(TM,UM)是使一阶导数达到最大值的点，也即城镇化增长速度最快的时间点以及其对应的城镇化水平；(TU,UU)是使二阶导数达到最大值的点，也即城镇化增长加速度达到最大值的时间点以及其对应的城镇化水平；(TL,UL)是使二阶导数达到最小值的点，也即城镇化增长加速度达到最小值的时间点以及其对应的城镇化水平。

第一阶段（(TU,UU)之前）：该阶段城镇化水平相对较低，增长速度较缓慢，加速度不断增加直至最大值；第二阶段（(TU,UU)，(TL,UL)之间）：该阶段城镇化水平快速提高，增长速度不断增大至(TM,UM)达到最大值之后开始逐渐减小，同时该阶段加速度不断减小，(TM,UM)之前加速度为正值，(TM,UM)之后加速度为负值并在(TL,UL)达到最小值；第三阶段（(TL,UL)之后）：该阶段城镇化率处于较高水平且仍继续缓慢增长，增长速度逐渐减小并趋近于零，加速度由最小值逐渐提高且向零逼近。

可以求出(TM,UM)，(TU,UU)，(TL,UL)三点的具体值如下。

首先对Logistic回归方程求二阶导数，(TM,UM)点对应横坐标值应为使二阶导数等于零的自变量值。

Logistic回归方程为：

一阶导数表达式为：

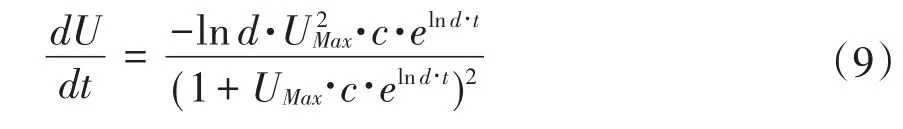
二阶导数表达式为：

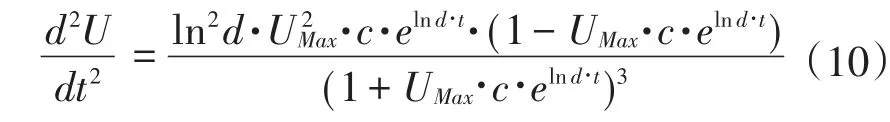
则 当 1-UMax·c·elnd·t=0 时 ，也 即 当 TM=-时，此时城镇化率增长速度达到最大值，此时的城镇化率为：

又，(TU,UU)，(TL,UL)的横坐标值应是使三阶导数等于零的自变量值，对（10）式求导，

三阶导数表达式为：

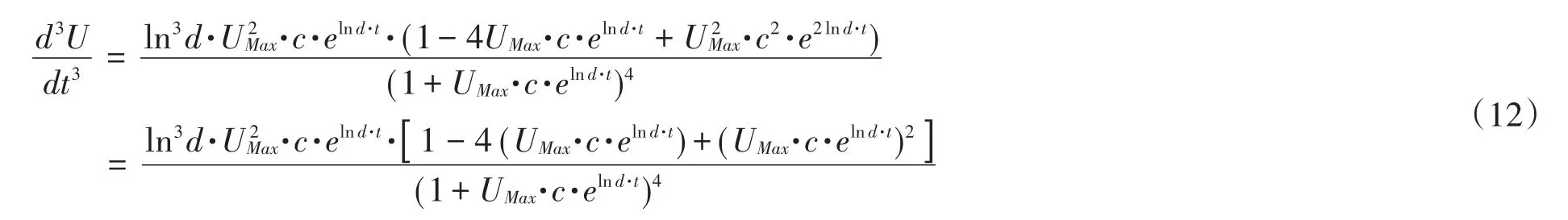
令T=UMax·c·elnd·t，则当 T2-4T+1=0时可求得，也即，

将TU，TL代入（12）式得到此时对应的城镇化率为：

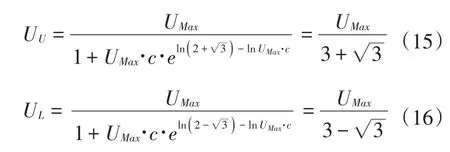
则：

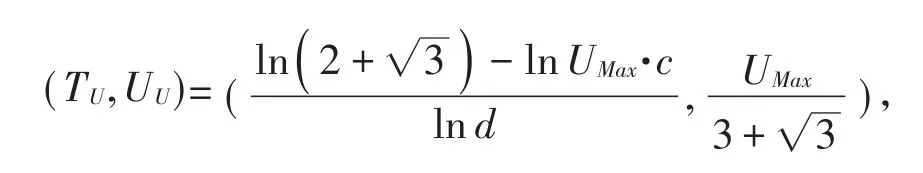
（四）数据来源

鉴于韩本毅在研究中表明，中国城镇化进程从1978年之后逐步体现Logistic曲线的特征[14]，本文采用1979～2014年全国各省、直辖市、自治区（将重庆市相关数据并入四川省以方便计算）年末城镇人口与总人口比值计算各省市城镇化率，所有数据均来自国家统计局发布的《新中国60年统计资料汇编》，缺失的数据由各省统计年鉴数据予以补足。

四、实证分析

（一）中国各省、直辖市、自治区城镇化率的面板数据聚类分析

本文对中国30个省、直辖市、自治区的36年间城镇化率相关数据采取前述方法进行聚类分析。通过专家评分法，本文将综合加权欧式距离的测算中所需权重系数分别赋予α=0.71，β=0.24，γ=0.05，利用Java编写程序进行聚类，并生成谱系聚类树状图如图4。

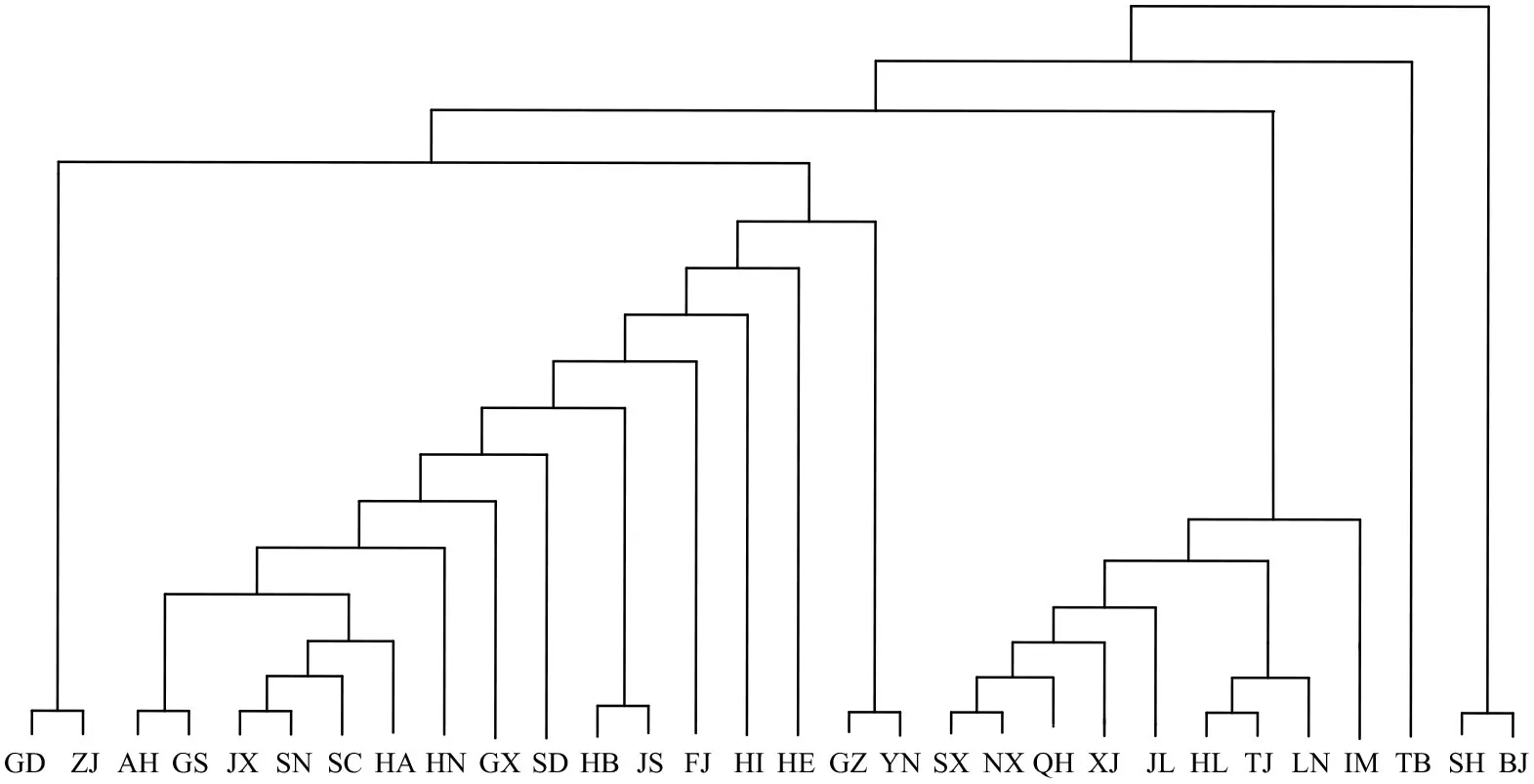
图4 基于综合加权欧式距离与Ward法的中国各省城镇化率聚类分析谱系树状图

本文最终将30个省、直辖市、自治区分为6类。表1给出了基于综合加权欧式距离聚类的分类结果：第一类：北京、上海；第二类：西藏；第三类：内蒙古、辽宁、天津、黑龙江、吉林、新疆、青海、宁夏、山西；第四类：云南、贵州；第五类：河北、海南、福建、江苏、湖北、山东、广西、湖南、河南、四川、陕西、江西、甘肃、安徽；第六类：浙江、广东。

表1 基于综合加权欧式距离与Ward法的中国各省城镇化率聚类结果

（二）中国城镇化率的Logistic增长模型回归分析、阶段划分及预测

1.中国城镇化率的Logistic增长模型回归分析及阶段划分

关于UMax的确定方法较多，国内外相关学者均对该值进行了相关推导与预测，国务院发展研究中心在《中国城镇化——前景战略与政策（2010）》中预测了中国城镇化水平的峰值，约为80%。本文立足于中国国情，亦参考这一权威数据。在本文中，假定各类省份的城镇化率上限均相等且等于全国城镇化率上限，又考虑到第一类省份（北京、上海）的平均城镇化率在2014年就已经达到87%以上，故本文将城镇化率上限设定在90%。

利用第三章第一节中聚类分析分类结果（表1），本文采用每类城镇化率重心代表该类的城镇化整体水平，以时间为自变量，以各类城镇化率水平重心为因变量，以类别划分横截面建立面板Logistic增长模型，拟合图像如图5所示。

可得到回归方程为：

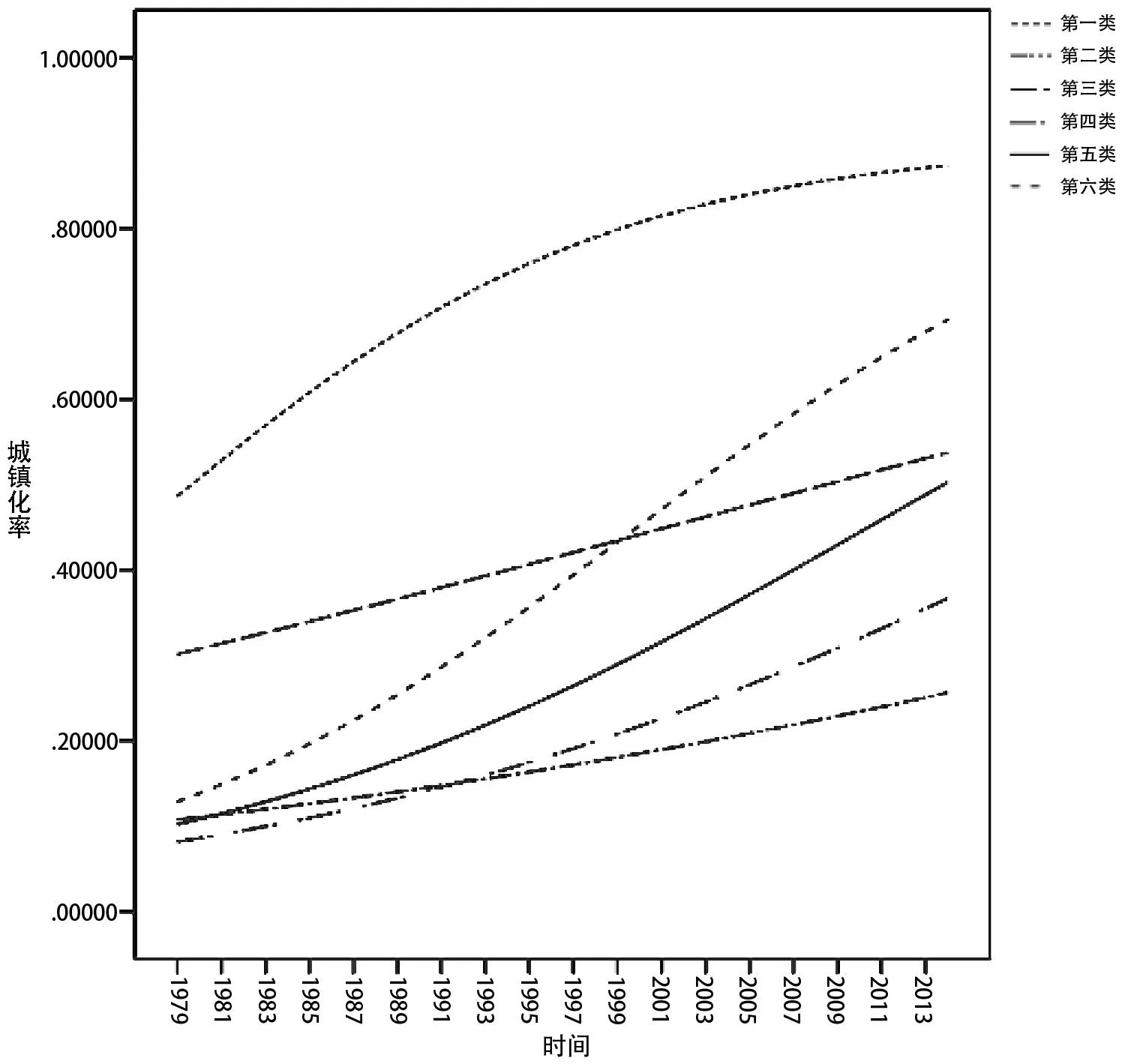
图5 1979～2014年各类省份面板数据Logistic增长模型回归曲线拟合

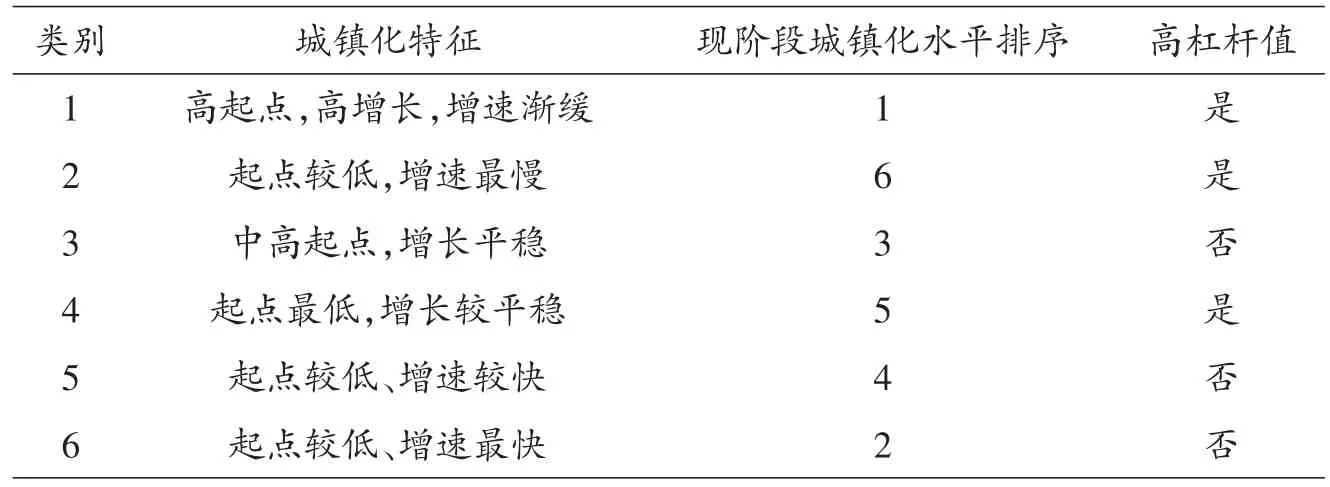
表2 各类省份城镇化特征及现阶段城镇化水平排序

回归方程调整R2为0.978，除第一个面板的回归常数外其余各参数均在0.01显著水平下显著，证明回归模型拟合较好。分析图5可得出如下信息：第一类（北京、上海）的城镇化水平在全国各类省份中处于最高水平；第二类（西藏）、第四类（云南、贵州）的城镇化水平在全国各类省份中处于最低水平；其余各类均处在中间水平。

进一步分析图5可知，第一类（北京、上海）城镇化水平从本文测度范围的起始点处就远高于其余各类省份，且该类省份在上世纪90年代之前一直保持较高的增长速度，从本世纪初开始，该类省份已逐渐达到发达国家的城镇化水平，城镇化率继续增长，增长速度逐渐放缓；第三类（内蒙古、辽宁等）城镇化水平在本文测量范围的起始点处处于中高水平，且在整个测度范围内城镇化率增长速度保持相对稳定；第五类（河北、海南等）、第六类（浙江、广东）城镇化水平从本文测量始点起处于较低水平，在整个测度范围内两类省份城镇化率增长速度均不断增加，而第五类省份城镇化率增速相对第六类省份变化较缓，截至2014年，第五类省份逐渐逼近第三类省份的城镇化水平，接近世界平均城镇化水平，而第六类省份在测度时期内城镇化率始终保持较高速度增长，至2014年已接近一般发达国家的城镇化水平；第二类（西藏）、第四类（云南、贵州）城镇化水平自测量始点起就处于全国最低水平，两类省份在整个测量时期内均保持较缓慢的增长，且增长速度均有所增加。各类省份城镇化特征描述及现阶段城镇化水平排序列于表2。

第一类、第二类以及第四类省份的城镇化率值与其余各省份偏离较远，在拟合回归中如同高杠杆值，可能导致回归曲线拉向高杠杆值方向从而造成回归不准确。考虑到第一类省份受国家政策导向，城镇化建设均早于全国其他省份；第二类、第四类省份地处全国最西南，其地势多为山区，城镇化建设较难且起步较晚，故以上三类省份均不适宜代表中国城镇化发展状况。为了较准确地测度中国整体城镇化水平，本文利用上述聚类分析结果，本文剔除城镇化率远高于大多数省份的第一类（北京、上海）省份和较低于其他省份的第二类（西藏）和第四类（云南、贵州）省份，选取其余各省份的城镇化率重心作为中国整体城镇化率水平，以此方法计算，兼顾了各省市城镇化水平的独特性和全国整体水平的一般性。根据以上分析，回归后可得到中国城镇化水平的Logistic回归曲线如图6。

得到回归方程为：

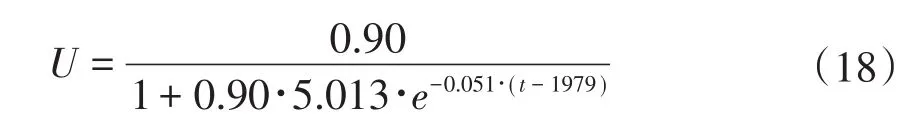
回归方程调整R2为0.969，模型拟合较好。

计算由本文所述方法测定的中国城镇化水平与国家统计局依照传统方法测定数据的偏差如表3所示。

可见，通过本文所述测量方法得到的城镇化率整体趋势和国家统计局数据较为接近，具有一定科学性，同时又排除了高杠杆值影响，对国家统计局数据进行了适度修正。

根据前面的结论又可计算城镇化率增长曲线的三个分界点的坐标：

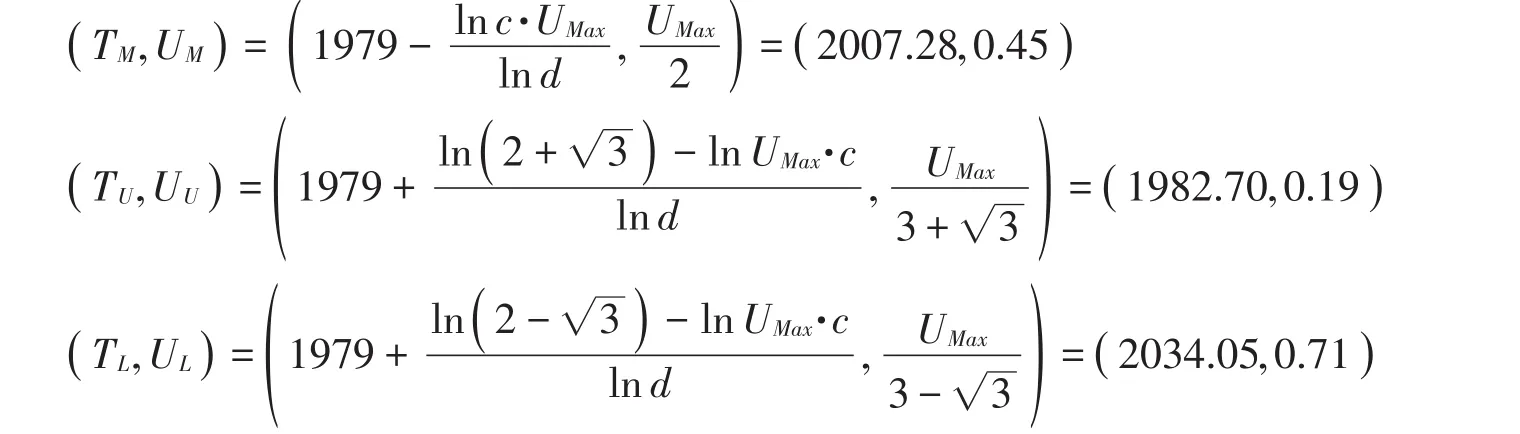
由计算结果可知，约在2007年前后，中国城镇化率增长加速度为零，此时增长速度达到顶峰，全国城镇化率为45%。中国城镇化快速发展阶段为1982年至2034年共约53年，这一阶段始终保持较高的城镇化率增长速度，城镇化率加速度不断减小，至2034年，城镇化率加速度达到最小。1982年之前，中国城镇化处于起始期，城镇化率加速度不断提高。2034年之后，中国城镇化开始逐渐进入末尾期，这一阶段中国城镇化率处于较高水平，城镇化率增速仍不断减小。综上所述，当前中国正处于城镇化快速发展阶段后期，这一阶段城镇化率仍保持相对较高的增长速度，但增长速度逐渐下降，城镇化率的加速度已为负值且不断减小。

图6 1979～2014年中国城镇化水平的Logistic回归曲线拟合

2.中国城镇化率趋势预测

根据前文中得出的结论，对中国城镇化未来近40年的发展态势进行预测如图7。

根据图7，结合第三章第二节第一部分中相关分析可以看出，中国城镇化水平在未来40年内仍会持续增长，增长速度不断放缓，预计2034年达到中国城镇化进程中的(TL,UL)点，即城镇化率加速度最低点。2015年至2034年的时间段内，中国城镇化率加速度始终为负值且不断降低。2034年之后，中国城镇化率加速度仍为负值但逐渐增大。按本文所建立的模型预测，直至2050年中国总体城镇化率可达到80.48%，逐渐接近中等发达国家的城镇化水平。

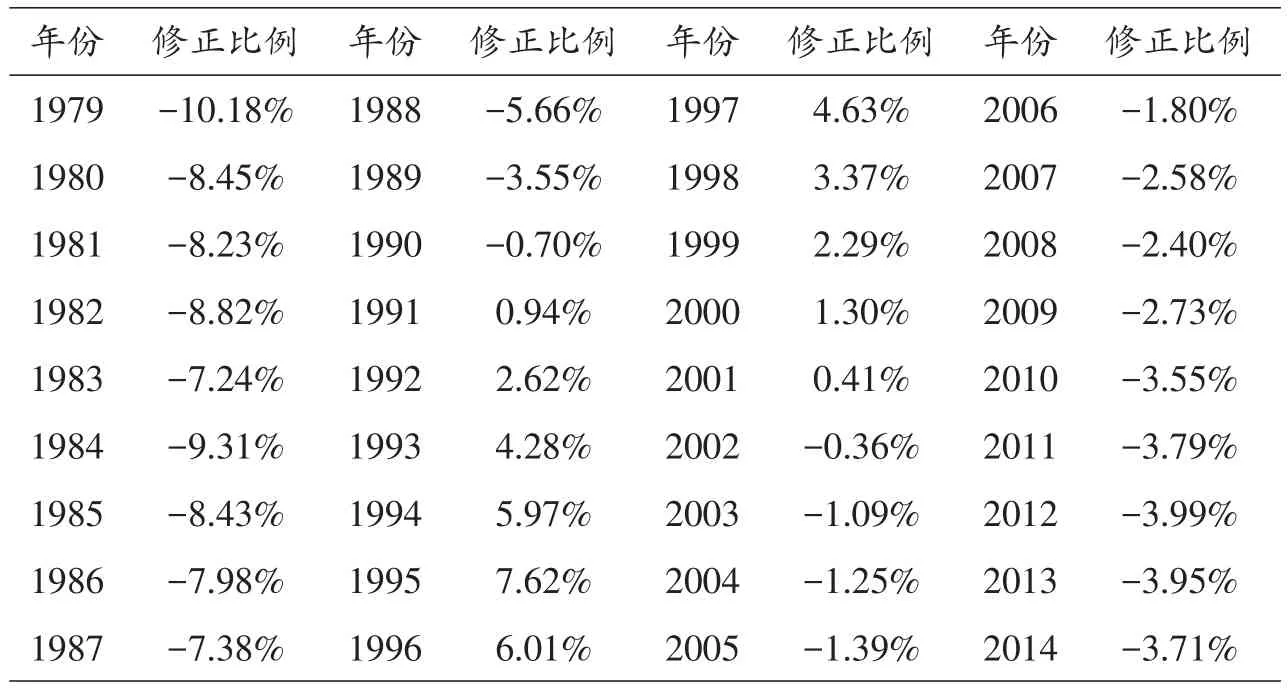
表3 本文方法测量数据对国家统计局数据的修正比例

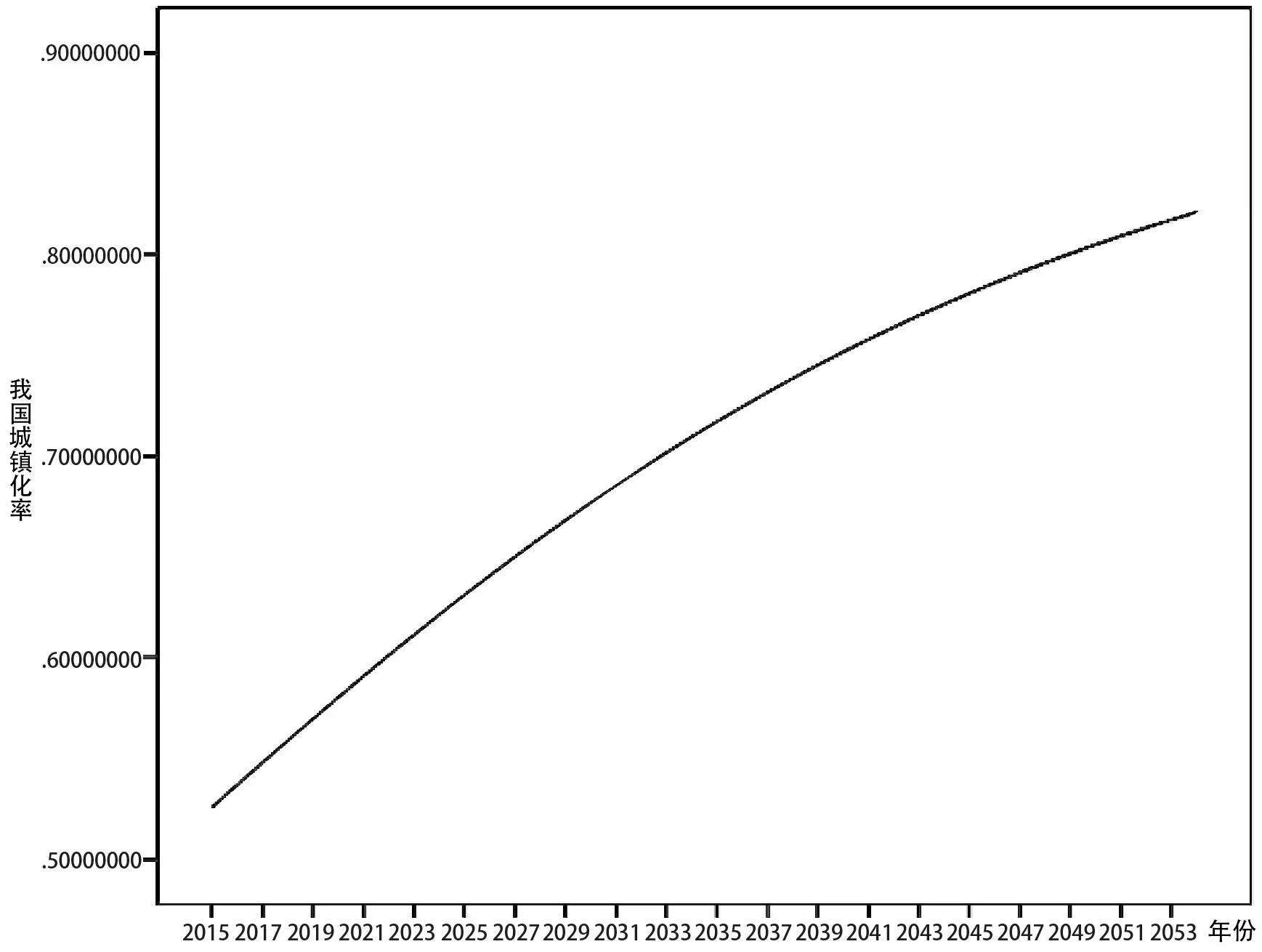
图7 中国城镇化率预测的Logistic回归曲线拟合

五、结论与启示

（一）结论

借鉴了前人的研究方法与思路，考虑到按地理因素对省份进行分类的不足之处，本文对中国30个省份36年的城镇化率数据进行聚类分析。依据综合加权欧氏距离将各省份分为六类，即：第一类（京、沪），第二类（藏），第三类（蒙、辽、津、黑、吉、新、青、宁、晋），第四类（云、贵），第五类（冀、琼、闽、苏、鄂、鲁、桂、湘、豫、川、山、赣、甘、皖）和第六类（浙、粤）。对各类省份的城镇化率进行面板数据Logistic增长模型回归后，分析了各省份的城镇化发展特点，其中第一类省份由于“起点高且增速快”位于各类省份中第一梯队；第三、五、六类省份由于“起点高或增速快”位于各类省份中第二梯队；而第二、四类省份则由于“起点低且增速慢”位于各类省份中第三梯队。由于第一、二、四类与其余各类省份城镇化水平差距较大，可视为高杠杆值，可能对最终回归结果产生影响。在排除高杠杆值问题的基础上，依据模型求出中国城镇化发展过程中的阶段分界点，说明了中国正处于城镇化发展的快速发展阶段后期。最后，本文对未来40年中国城镇化的发展进程进行预测。数据表明，在未来40年内，中国城镇化水平仍会不断提升，但提升速度逐渐放缓，至2050年中国城镇化率将逐渐接近中等发达国家的城镇化水平。

本文对面板聚类分析中距离测度方式进行改进，加入了加速度欧氏距离指标，在聚类分析中综合考虑了城镇化发展的历史与现状、经济和政治等因素，使可以更完善地描绘城镇化率的演变过程，以更好地实现聚类。在此基础上又对中国城镇化率的测度方法进行了优化，减小了高杠杆值对全国城镇化率的影响，兼顾了各地区城镇化进程的特殊性与一般性，使对城镇化率的测度方法更系统化、客观化。本文所述方法将有助于把握当前城镇化发展形势，明确中国城镇化所处阶段，为制定未来城镇化战略性指导政策提供科学理论依据。本文在对中国30个省份的城镇化率数据进行面板聚类分析时仅考虑到各省份城镇化率的关联而没有考虑到地域联系，下一步研究可以在本文的分类方法基础上进一步分析区域城镇化发展，为各区域可持续发展和城镇化提供更为详细的政策制定参考。

（二）启示

改革开放以来，中国城镇化发展取得了可喜的成果，经济发展态势不断向好，总结改革开放前以及当今的经验教训，符合中国经济发展需求的新型城镇化发展道路是推动城镇化健康发展的关键。根据本文相关结论，对中国城镇化发展提出以下建议：

第一，着力开展集约型城镇化建设。当前中国处于城镇化快速发展阶段后期，城镇化发展速度较快，但增速逐年减缓。面对城镇化增速下降的必然趋势，粗放扩张式城镇化路线将越来越不可取。改革开放以来，我国采用此方式开展城镇化建设，并取得优异的建设成果。然而，此方式带给我们的不仅仅是城镇化水平和国内生产总值的快速增长，亦透支了环境福利和土地福利等。随着城镇化建设进一步深入，在已经到来的城镇化发展新时期和城镇化增速减缓新趋势下，粗放式发展只能带来城镇化建设效益递减以及远高于产出的生态环境破坏和治理成本。为此，应着力开展集约型城镇化建设，依据城市地理区位、资源禀赋、市场条件和交通运输等因素，合理进行城镇化建设规划与定位，以提高城市城镇化建设投入产出比和城镇化建设效率。同时，应正确处理好人口、资源与环境等诸多方面的制约关系，做到早发现早治理，开展可持续城镇化建设。

第二，加快并扩大城市群建设。从依据中国各省市城镇化发展状况的分类结果中可以看出，除第二类（西藏）外，其余各类均包含不少于两个省份。每类省份的城镇化发展模式相似，其社会、经济、地理、人文等方面必然存在相似之处，同类型的省份共同开展城镇化建设，相互依托相互扶持，可以使城镇化建设由以省为单位扩展为以区域为单位，加大城市中心辐射范围，增强城市规模效应，更有利促进城镇化建设与区域经济发展。结合因地制宜的城镇化发展政策，在每类省份中求同存异，兼顾了每个省份的特殊性与每一类省份的一般性，从而使全国城镇化水平整体性提升。

第三，城镇化建设重心应逐渐向内陆转移。第一类（京、沪）和第二类（浙、粤）省份城镇化水平在全国范围内领跑。分析中国各省份城镇化指标也可发现，沿海省份城镇化水平较内陆地区普遍偏高。这在一定程度上是由于改革开放、区位交通因素等诸多政策及地理条件而引起的。随着交通、物流、运输业等的发展，区位因素的重要性逐渐下降；而伴随着“振兴东北老工业基地”、“西部大开发”等政策的颁布与实施，也逐渐平衡了内陆与沿海地区的政策支持。整体提升全国城镇化水平仅依靠沿海地区是不够的，更需要依靠广阔的内陆地区。在城镇化建设的新时期，应逐渐缩小沿海省份与内陆省份城镇化差距，沿海省份带动内陆省份，实现沿海、内陆城镇化协调增长。

第四，加大对西南部省份的城镇化发展建设力度。第二类（藏）、第四类（云、贵）省份整体城镇化水平在全国各省份中处于最低的水平，此类省份大都处于西南边境地区，经济发展多依靠旅游业带动。自改革开放以来，该类省份城镇化增长速度均较为缓慢，应制定相应政策加大对该地区的城镇化建设力度，可通过产业结构调整，利用其资源优势，着力发展第三产业，充分发挥“结构红利效应”，开发及合理利用当地自然禀赋以调节生产要素的供需结构，推动旅游业建设与发展。在发展第三产业同时，积极把握产业间的关联效应和扩散效应以带动第一、二产业同步发展，诱导新技术、新原料等需求的出现以推动经济发展，以使其城镇化率增长速度得到提升。从而缩小这一地区与其他区域城镇化水平差异，带动全国整体城镇化水平提升。

[1]Northam，R.，M.Urban Geography（2nd ed）[M].New York：John Wiley&Sons，1979.

[2]王远飞，张超.Logistic模型参数估计与我国城市化水平预测[J].经济地理，1997，17（4）：8-13.

[3]乔松珊，孙成金.优化的Logistic模型及其在城镇化水平预测中的应用[J].许昌学院院报，2016，35（5）：10-15.

[4]王帅，滕玉成.基于Logistic模型的县域城镇化率及其推进预测——以济南市平阴县为例[J].西安建筑科技大学学报（社会科学版），2014，33（6）：32-37.

[5]赵文英，葛礼霞.基于改进Logistic模型的黑龙江省城镇化水平预测[J].数学的实践与认识，2013，43（13）：44-49.

[6]陈彦光，周一星.城镇化Logistic过程的阶段划分及空间解释——对Northam曲线的修正与发展[J].经济地理，2005，25（6）：817-822.

[7]冯年华，宣卫红，戴军，王书明.基于Logistic模型的我国城镇化演进轨迹分析[J].生态经济，2015，31（7）：76-79.

[8]王建军.城镇化发展阶段划分[J].地理学报，2009，64（2）：177-188.

[9]陈素平，张乐勤，许信旺.基于Logistic模型的中国城镇化演进阶段特征及趋势探析[J].干旱区地理，2015，38（2）：384-390.

[10]张乐勤，张勇.基于Logistic模型的中国城镇化快速演进期时长、速度及启示[J].河南大学学报（自然版），2015，45（5）：550-555.

[11]Bonzo D.C.，Hermosilla A.Y.Clustering Panel Data via Perturbed Adaptive Simulated Annealing and Genetic Algo⁃rithms[J].Advances in Complex Systems，2002（4）：339-360.

[12]Ren J.，Shi Sh L.Multivariable Panel Data Ordinal Clus⁃tering and Its Application in Competitive Strategy Identifica⁃tion of Appliance-wiring Listed Companies[C].International Conference on Management Science&Engineering（16 th），Moscow，Russia，2009：253-258.

[13]李因果，何晓群.面板数据聚类方法及应用[J].统计研究，2010，27（9）：73-79.

[14]韩本毅.国城市化发展进程及展望[J].西安交通大学学报（社会科学版），2011，31（3）：18-22.