液浮陀螺加速度计温度场计算与分析

张福礼，刘 钦，王 昕

(北京航天控制仪器研究所，北京 100039)

陀螺加速度计是组成惯性平台测量系统的关键仪表，可精确地测量载体相对惯性空间的线运动，给出载体的加速度、速度和位置信息，主要用于火箭或导弹的控制系统。其性能对惯性平台的精度及可靠性具有关键作用[1]。

陀螺加速度计由浮子、摆和外环组件组成。摆内部充高比重浮油，实现浮子的无接触全液浮支承。摆内部温度梯度的大小对仪表影响很大，可引起浮油流动、热应力不对称，从而产生附加力矩或剪切应力，影响仪表精度；因此，进行温度场计算和分析是仪表热设计的关键环节[2]。

1 ANSYS Fluent软件在传热模拟中的应用

Fluent软件是用于计算流体流动和传热问题的软件[3-4]，涉及流体、热传递及化学反应的工程问题都可以应用Fluent软件进行解算。Fluent软件是基于有限体积法(FVM)对控制微分方程进行离散化的，有限体积法可视作有限元法和有限差分法的中间产物。有限体积法适于流体计算，可以应用于不规则网格，适于并行，其优势正逐渐的被显现出来。

利用Fluent软件进行解算时，首先利用其前端软件Gambit进行几何形状的构建、定义边界类型和生成网格；然后在Fluent软件中读取Gambit软件所输出的网格文件，设置边界条件，完成对几何区域的求解计算；最后对计算的结果进行后处理。

传热是物质在温度差作用下所发生的热量传递过程，传热有3种基本方式：传导、对流和辐射。只涉及热传导或对流的传热过程是最简单的情况，而涉及到浮力驱动流动或者自然对流、辐射传热的过程却比较复杂。依据问题的不同，Fluent软件求解不同的能量方程。

在流体区域，Fluent使用的能量方程形式如下[5-6]：

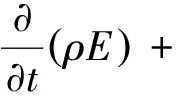
(1)

(2)

(3)

式中，T为温度；Tref为298.15 K；cp为比定压热容。

式1右边的前3项分别表示由于热传导、组分扩散、粘性耗散而引起的能量转移。而在固体区域，Fluent软件使用的能量方程形式如下：

(4)

2 陀螺加速度计热分析及模型的建立

2.1 陀螺加速度计的热分析

陀螺加速度计主要由浮子组件、大小护线板组件、摆组件和外环组件组成，热生成元件有陀螺马达、内环传感器、磁悬浮、加热片、力矩电动机和外环传感器。将加热片定义为外热源，其他元件均定义为内热源，具体分析如下。

1)内热源。陀螺马达是仪表的主要内热源，其输入功率大部分转化为热量，一部分是定子绕组的铜损和铁损热量，这些热量经定子铁心、马达轴，沿浮子支架至支架的两端板传导到浮筒的内壁；另一部分是风阻发热，其通过浮筒内的氦气由马达转子高速旋转将热量以强迫对流的方式传到浮筒内壁，这2种热量经浮筒传给浮油和壳体；内环传感器和磁悬浮元件为绕组发热，电流、功率均较小，可以忽略。力矩电动机和外环传感器为绕组发热，热量通过外壳体传导散出。

2)外热源。外热源加热片贴在摆上，主要是通过热传导将热量经过壳体传至浮油薄膜上，使其保持在工作温度70 ℃[7]。

2.2 仿真模型的建立

陀螺加速度计结构复杂，仿真模型的建立是前期的一项重要工作，既要保证计算模型与真实模型在结构、尺寸上的一致性，又要保证模型的计算效率。几何模型的建立是在Fluent软件的专用前处理器Gambit的软件平台上完成[8]。建立了零组件数值模型、浮子内部的氦气模型、摆组件内部与浮子之间的浮油模型以及仪表壳体内部与摆之间的空气模型，气体和液体模型在Fluent软件中均以流体处理。建立零组件模型的时候，对于一些细小的特征如小圆角、小孔、微间隙等对温度场影响不大的部位进行了简化处理。最终仪表整体温度场仿真模型如图1所示，仿真模型网格如图2所示，浮油的数值模型如图3所示。

图1 陀螺加速度计温度 图2 陀螺加速度计仿真场仿真模型 模型网格

图3 陀螺加速度计浮油的数值模型

2.3 材料及边界条件的确定

2.3.1 材料属性

仪表油黏性大，在分析过程中作为固体材料来处理。即假设仪表油的温度在工作状态下相对均匀分布，不发生流动。浮筒内部的氦气以及摆和仪表外壳之间的空气均作为理想气体。

2.3.2 边界条件

1)内热源的设定。马达功率约为2.5 W、传感器功率约为120 mW、力矩电动机功率约为75 mW。

2)外热源的设定。加热片功率，稳态电流为150 mA，则三部分加热片功率分别为0.35 W、2.52 mW和0.28 W。

3)外界对流条件的设定。环境温度设定：整表+外温控的温控点为55 ℃；表面传热系数设定：5 W/(m2·℃)。

4)氦气当量表面传热系数的设定。马达高速旋转，带动氦气流动，形成强迫对流换热，可简化为气体掠过平板的换热模型。其计算公式如下：

λe=Nμλ

(5)

5)空气当量表面传热系数的设定。仪表进动角速率为1.05 rad /s，使摆与仪表外壳之间的空气也存在强迫对流换热，依据上述公式和空气参数计算得λe=0.151 W/(m·℃)，相对静态空气的表面传热系数0.025 6 W/(m·℃)，增大了约6倍。

3 仿真结果及分析

采用Fluent软件对仪表进行了仿真计算，得到了仪表的温度分布、温度梯度等信息。

陀螺加速度计X-Y剖面的温度分布如图4所示，仪表X-Z剖面的温度分布如图5所示。

图4 X-Y剖面温度分布

图5 X-Z剖面温度分布

由图4、图5可得如下结果：

1)仪表最高温度在马达绕组上，为71.9 ℃，紧邻外温控的仪表外部温度最低，为64.6 ℃，温差为7.3 ℃。这种温度梯度主要是因为仪表热耗通过摆与壳体间的空气对流换热的热阻大，以及仪表与外温控间表面传热系数较小引起。

2)摆组件沿Y向的最大温度为69.4～71.9 ℃，温度梯度为2.5 ℃，摆沿Z向的最大温度为69.8～71.9 ℃，温度梯度为2.1 ℃，由此可得，整个摆外壁的温度差<0.4 ℃，温度差较小。

浮油整体以及浮子径向油膜的温度分布如图6所示。

图6 浮油整体以及浮子径向油膜的温度分布

通过浮油温度场分布可得如下结果。

1)靠近轴向磁悬浮磁片位置浮油的温度最高为71.2 ℃，这是因为氦气热阻较大，马达的热量主要通过马达支架散出，磁悬浮磁片直接粘接在支架上距离马达最近的位置，导致此处浮油的温度比油膜的最高温度71 ℃还高0.2 ℃。

2)大护线板端浮油温度为69.9 ℃，小护线板端浮油温度为70.2 ℃，温差为0.3 ℃。这主要与两端加热片功率比和两端散热面积比有关，计算可得：W大/W小=1.24，而S大/S小=1.36。相对散热面积而言，大端加热片的功率稍小，引起0.3 ℃的浮油温差。

3)油膜温度为70.7～71.0 ℃，温差为0.3 ℃。浮子两端温度略高，中间略低，与马达热传导路径的分析一致。而对于这种温差是否能够造成高黏度浮油的微流动，并形成干扰力矩，需进行进一步研究和分析。

氦气温度分布和等速流线分布如图7所示。由图7可以看出，陀螺电动机转子的高速旋转带动氦气流动，靠近飞轮的地方速度高些。由于氦气黏度的存在，进而带动其他部位的氦气以较低的速度流动，形成强迫对流换热。

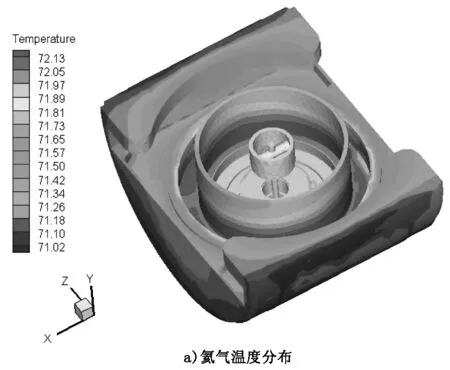
图7 氦气温度分布和等速流线分布

4 特殊位置的温度测试

本文采用仪表不同位置元件绕组阻值随温度变化的特性进行了摆特殊位置的平均温度测试，其方法是先通过温箱来对各个绕组的温度系数进行标定，然后通过此温度系数来推算各点的温度值，作为绕组整个区域的平均温度。推算绕组所在位置温度的算式为t=(Rx-Rl-K0)/K1，结果见表1。

表1 陀螺加速度计不同位置的温度

从表1可以得出：1)马达绕组比浮子两端温度稍高，为70.28 ℃，比左端磁悬浮绕组位置高0.18 ℃，比右端高0.43 ℃；2)浮子右端比左端温度稍低，这在温度场设计中给予了考虑，右端小加温片1的功率比左端小加温片2大，但从试验数据来看，右端功率仍须增大；3)感温电阻与测温电阻显示的温度差为0.06 ℃，表明感温电阻与测温电阻的位置选取十分合适。

从仿真计算结果中提取与温度实测位置对应的温度信息，结果见表2。由表2可以得出：1)仿真结果显示的温度梯度趋势与实测一致，表明对仪表模型施加的热功率条件正确；2)仿真计算结果比实测均偏高，分析主要是与表面传热系数误差、绕组实测的平均温度与仿真提取的单点温度差异有关。这种误差对温度场趋势判断无影响。

表2 实测与仿真结果数据对比

5 结语

本文在考虑外环元件热生成和摆外部空气保温作用的情况下，建立了完整的陀螺加速度计分析模型。利用Fluent软件得到了整个仪表的温度场分布，并通过测量绕组阻值变化的情况对仪表温度场进行了特殊位置的测试，验证了陀螺加速度计温度场分析的正确性，以及在结构受限情况下采用绕组阻值进行温度测试的可行性，为改进陀螺加速度计的热设计和提高陀螺加速度计精度提供了依据。

通过分析和测试得到如下结论：1)仪表摆右端的加热片功率仍略小，左右两端存在0.3 ℃的温度梯度，梯度较小，分析与空气的保温作用有较大关系；2)浮油的综合温差为0.3 ℃，但理论上此温度差对浮油运动驱动作用尚不清楚，因此这个量级温度差的影响尚需研究；3)仪表内壳体上2个感温电阻位置几乎无温度差，表明上、下枢轴直径以及轴承尺寸不同对热传导的影响，可通过传感器和力矩电动机的热生成部分抵消。

[1] 杨立溪. 国外惯性技术的发展现状与展望[J].导航与控制, 2004, 3(2):58-62.

[2] Appel N, Holland J, Levine A, et al. Three dimensional finite element analysis of inertial gyros[C]//Guidance and Control Conference, Hollywood, Fla., August 8-10, 1977, Technical Papers. New York:American Institute of Aeronautics and Astronautics, Inc., 1977.

[3] 杨世铭, 陶文铨.传热学[M]. 4版.北京:高等教育出版社, 2006.

[4] 杨盛林,刘昱,刘玉峰.惯性平台热场分析及热设计的改进[J].中国惯性技术学报,2005,13(1):5-9.

[5] 卜石, 刘娜.某型号液浮陀螺温度场分析与优化改进[J].导航与控制,2006,5(3):52-58,63.

[6] 任玉新, 陈海昕.计算流体力学基础[M].北京:清华大学出版社, 2006.

[7] 杨盛林,刘昱,刘玉峰.某型液浮陀螺仪定位壳体温度场有限元分析[J].中国惯性技术学报, 2004,12(5):43-48.

[8] 王福军. 计算流体动力学分析[M].北京:清华大学出版社, 2004.