供水管网爆管动态风险评估

曾 翰，柯 庆，周 超，陶 涛

（同济大学环境与工程学院，上海 200092）

1 研究背景

爆管是指管道发生的结构性损伤，管道漏水上升到地面，必须立即修复的情况［1］。近年来，城市供水管网爆管事故所造成的经济损失和社会影响不断扩大，严重影响了市民生活和城市安全，反映了城市基础设施的薄弱环节，对城市供水管网安全保障提出了更高的要求。加快现代高新技术在供水管网运行安全保障的应用已成为供水行业和科技部门的迫切任务。

目前，如何对爆管事故进行科学有效地预防和预测仍然是实现供水管网可持续管理所面临的一项主要挑战。针对压力管道爆管的研究已经进行了近50 年，在爆管预测方面，1979 年，Shamir等［2］认为爆管的次数与管龄呈指数关系，提出了管道爆管率的回归分析方法，这种基于管龄的模型能够较好地对管网爆管进行宏观预测，但是无法分析出爆管发生的确切时间和位置。2005年，Moglia等［3］同时考虑了爆管的统计概率以及管材的物理特性，提出了物理概率失效模型。类似的统计模型在Kleiner等［4］、Scheidegger等［5］、Gat［6］的研究中也有报道。

爆管风险评估的研究主要集中在利用统计模型对爆管记录、管道特征以及地域特征进行分析，预测出管道在未来一段时间内的爆管风险率，评估的结果大多是一个固定的爆管率值，换句话说，这些结果是“静态”的。然而，供水管网的水力因素是随时间变化的，故爆管风险率也是时变的，即管道在一天之内，在水力条件良好的时段内处于安全等级，而在其他的时段（如压力剧烈波动的时段）则可能处于不安全等级。由于传统的评估方法没能深入发掘出爆管风险与动态水力因素的关系，这些方法在管道维护、更新等方面的应用受到了限制。因此，有必要开发出一种能够得到爆管风险与时间关系的评估方法，即“动态”方法。

本文首先对影响管段爆管的动态水力因素进行筛选，并确定其分级评价标准，然后，应用BP神经网络原理，分析待评价管段的水力状态与哪一分级标准更为接近，即把水力因素定量化为评价等级，构建一个供水管网动态爆管风险评估体系，进而配合管段爆管静态风险评价，实现对管网安全的综合评价。

2 动态水力安全评价指标的选择和量化

2.1 评价指标的选择

影响管段爆管的动态因素包括流速、压力、温度、路面载荷等，然而管段水流的实时温度和路面载荷数据一般较难获得，因此本研究主要考虑管道的动态水力因素，包括以下三点。

（1）管段流速

管段内水流的压力振荡幅度与管段的流速有关，流速越大，压力波动也越大，管段的爆管几率也会相应增大。因此对某一管道进行水力安全评价时，必须考虑管道中的流速。

（2）管段压力

尽管管段的运行压力不是引发爆管的主要原因，但是爆管发生的主要原因水锤的最大和最小压力变化与管网运行的压力有关。有的文章［7］中指出，管网运行压力对管道破坏造成的漏水与爆管几率随压力的增大而增加，因此本文考虑管段的平均压力（即管段两端节点压力的均值）作为评价指标。

（3）管段压力的变化幅度

当管段压力变化较为剧烈时，会使管壁和管段接口处产生延展形变，对管段的安全使用产生很大的影响，管段的爆管几率也即相应的变大。因此对某一管道进行动态爆管率风险评估时，必须考虑管道中的不同时刻之间的压力变化幅度。本文定义管段某个时间点的压力与其下一个时间点压力的差值作为该时间点的压力变化值，时间间隔为15 min。

2.2 评价指标的量化

本文根据所选案例管网的实际爆管统计情况以及爆管管段的流速、压力、压力差情况，将动态水力安全评价指标分为安全、低危险、危险和高危险4个等级，每个等级所对应的水力评价指标的取值范围如表1所示。

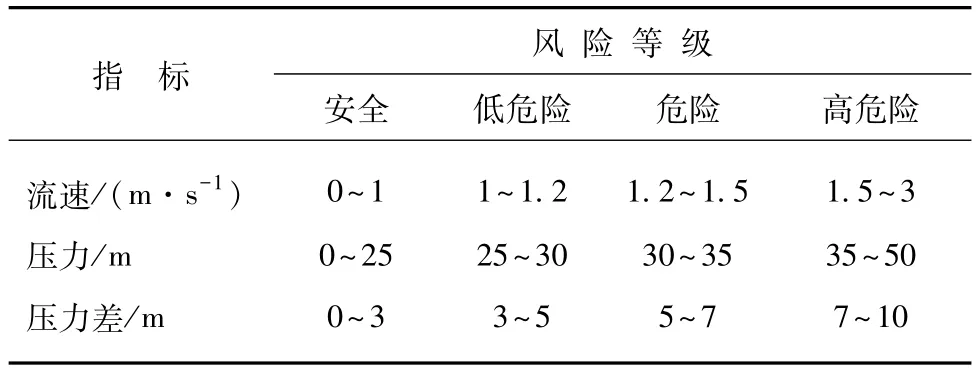
表1 爆管动态水力安全评价指标Tab.1 Evaluation Index of Dynamic__Hydraulic Safety for Pipe Burst

以管段的上述三个指标组成的评价指标向量的时间序列作为BP神经网络的输入，可以得到管段每个时间点的安全等级。

3 BP神经网络爆管动态风险评估

3.1 训练样本设计

BP神经网络又被称作误差反向传播（back propagation）神经网络。反向传播，顾名思义，一般是指对于误差的调整过程是从最后的输出层依次向前，逐层进行的。标准的BP神经网络一般是采用梯度下降算法，而对于网络权值则会沿着性能函数梯度进行反向的调整。

本文构建的BP神经网络模型以EPANET中管网水力模型的运行数据为输入，根据对上述三个水力参数的评价标准，对管段的整个动态运行状态进行分析。考虑到计算效率的问题，本文采取最基本的BP神经网络，它包括输入层、隐层、输出层这三层节点。

训练样本集的设计按如下方法进行：每个训练样本对应一个风险等级，假定水力评价指标按风险等级从低到高划分为N个等级，则训练样本集包含N组样本，其中第i组样本对应于风险等级的第i级（i＝1，2，...，N）。

第i组训练样本的期望输出向量的确定方法如下：第i组训练样本的期望输出向量是一个N维向量 （Y1i，Y2i，．．．，Yji，．．．，YNi），向量中的 N 个元素分别对应于N个风险等级，其中第j个元素的取值如式（1）。

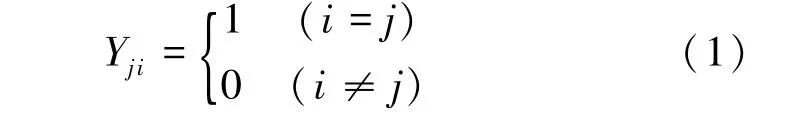
第i组训练样本的输入向量的确定方法如下：假设共有m种风险因子参与管网爆管的风险评估，首先将这m种风险因子的第i级风险等级的标准值组成一个 m 维向量（X1i，X2i，．．．，Xji，．．．，Xmi），其中，Xji表示第j种风险因子的第i级风险等级的取值。之后，对上述的m维向量进行标准化。第j种风险因子的第i级风险等级的标准值按照式（2）标准化。

其中，XjN表示第j种危险因子的第N级风险等级（即爆管风险最高的等级）训练样本中的最大值，X′ji表示标准化后的结果。对所有m种风险因子的标准值进行标准化后，得到新的 m维向量 （X′1i，X′2i，...，X′ji，...，X′mi），即为第 i组训练样本的一个输入向量。

如本文第2节所述，动态水力安全评价指标（风险因子）包括流速、压力和压力变化值3种，划分为4个等级，部分训练样本如表2所示。例如，假设某管段某时刻的流速、平均压力和压力变化值分别为1.26 m／s、30.82 m、5.76 m，根据表 1，三者的范围均在危险等级的范围内，则该样本处于危险等级，其期望输出向量为（0，0，1，0），假设高危险等级的训练样本中三者的最大值分别为 1.75 m／s、47.42 m、10.06 m，对样本的三个指标标准化后得到3维向量（0.72，0.65，0.57），该 3 维向量即为危险等级的一个输入向量。如果某个训练样本的三个指标值并不全在某一风险等级的范围内，则应根据经验和管网实际爆管情况判断该样本处于哪一风险等级。

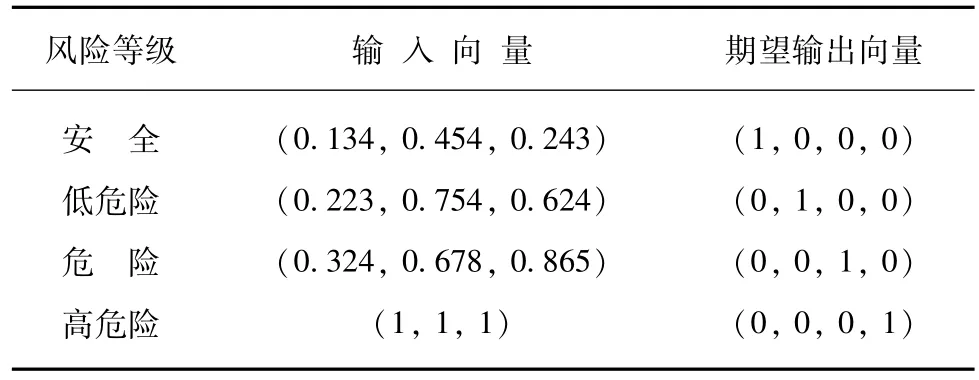
表2 训练样本表Tab.2 Training Samples

3.2 爆管动态风险评估

利用BP神经网络对管段的爆管风险进行评估，需要分成以下两个步骤来实现。

（1）训练数据。即利用上述的训练样本对神经网络进行训练，得到神经网络的隐层和输出层各节点的连接权值和阈值。

（2）利用已经训练完毕的神经网络对管段爆管动态风险进行评价。

利用BP神经网络对管网中的某根管段某个时刻的爆管风险等级进行评价的过程主要分为以下两步。

（1）从EPANET建立的水力模型中得到该管段该时刻的三个评价指标的数据，进行标准化后得到神经网络的输入向量。

（2）将上述的输入向量输入到神经网络中，得到一个输出向量。然后，根据最大隶属度原则可以得到该管段该时刻的风险等级，即在输出向量的N个元素中，哪个元素的数值最大，管段的爆管动态风险等级就处于哪一级。

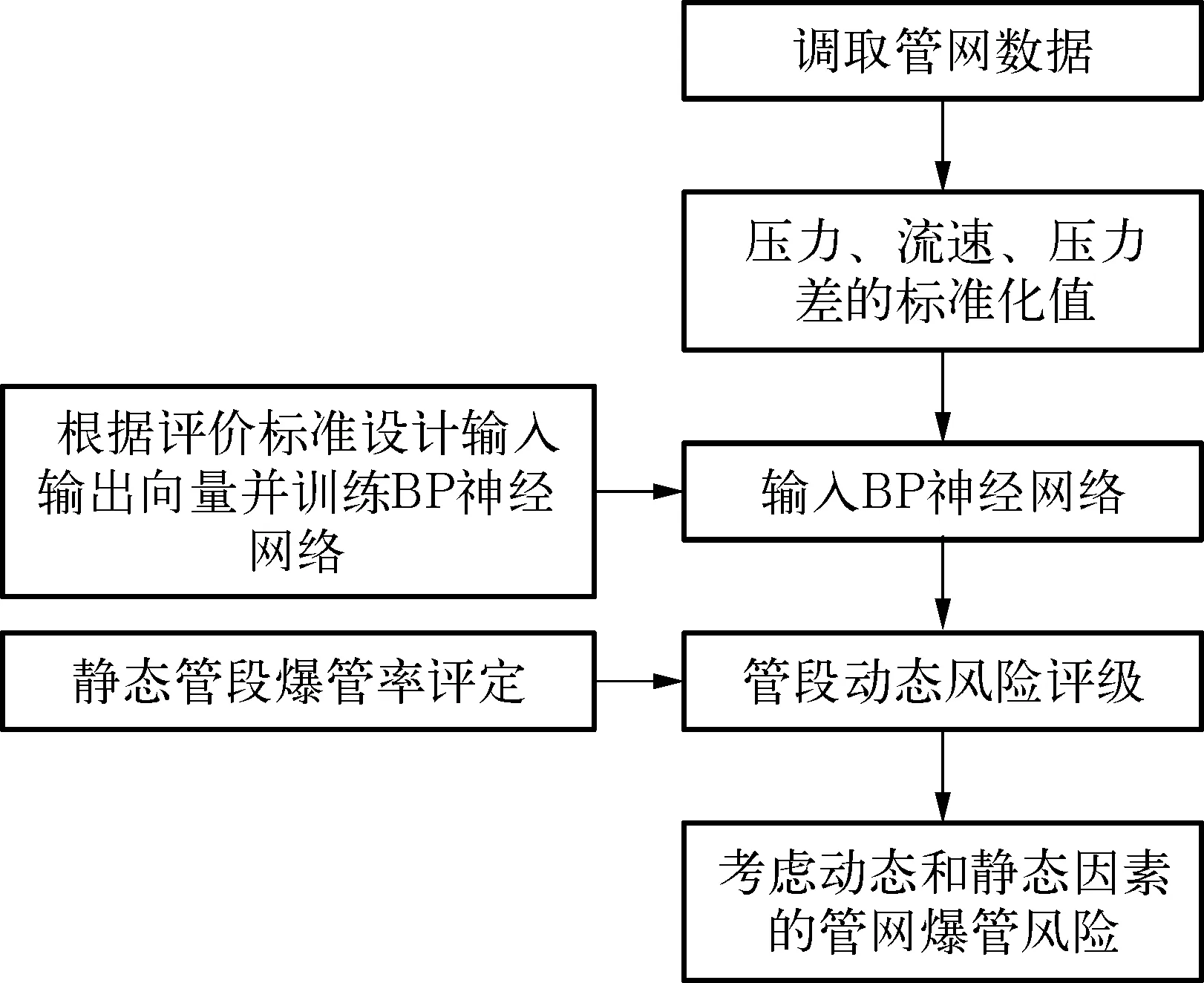
图1 BP神经网络动态风险评估流程图Fig.1 Flow Chart of Risk Assessment of Pipe Burst Dynamic for BP Neural Network

对管网的爆管风险进行综合评价的过程如图1所示，首先利用BP神经网络得到管段的动态风险等级，然后，根据动态风险等级可以对管段的静态爆管率进行修正，得到综合考虑动态和静态因素的爆管风险率。

本文的静态爆管率评定参考柯庆等［8］的爆管风险评估模型，该模型考虑的主变量是管龄t，协变量是管径X1和管材X2，如式（3）。

其中：h（t，X）—单位长度管段发生爆管的概率，次／（年·km）；

A，B，C，β1，β2—爆管风险模型参数。

根据得到的动态风险等级，对管段的静态爆管率进行修正，假设对管段的动态风险评估的输出变量为（Y1，Y2，Y3，Y4），每个时段的静态爆管率的修正系数可以由神经网络的输出向量的每个元素，乘以其对应的评价等级的权值，再把这些元素与权值的乘积进行加和得到，修正后的爆管率如式（4）。

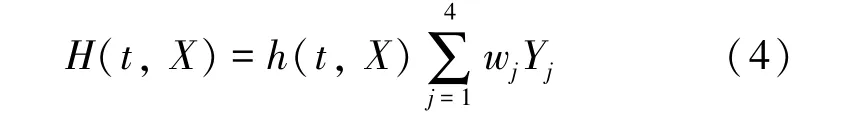
其中：H（t，X）—修正后的爆管率，次／（年·km）；

wj—第j级风险等级的权值。

本文中，权值主要根据经验确定，安全、低危险、危险、高危险四个等级的权值分别为1、1.2、1.5、2。

3.3 BP神经网络参数设置

本文的BP神经网络模型采用matlab的神经网络工具箱来构建，其主要参数设置如下。

（1）选择两层（只有一个隐层）BP神经网络结构；

（2）输入节点数为3（对应3个动态水力安全评价指标），输出节点数为4（对应4个评价等级）；

（3）隐层节点数为15；

（4）考虑样本的多样性以及代表性，样本空间容量设为1 000；

（5）输入层到隐层的传递函数选择tansig型函数，隐层到输出层传递函数选择purelin型函数；

（6）训练函数选择traindgm函数；

（7）网络的训练精度设定为0.01。

以预设的参数对BP神经网络进行训练，学习效率初始值为0.05，容量误差为0.001，学习样本数为96，网络经过555次训练后达到了预设的目标误差0.01。

4 实例分析

4.1 实例供水管网模型概况

本文用于爆管动态风险率评估研究分析的ZZ市供水管网模型如图2所示。对ZZ市管网模型进行简化，将管径300以下的管段去除，并根据管网的拓扑性质，在不影响管网水力特性的前提下，删减部分管段，将模型原来50 000多根管段，化简为25 000多根管径在300以上的管段，管网管段信息概况如表3所示。

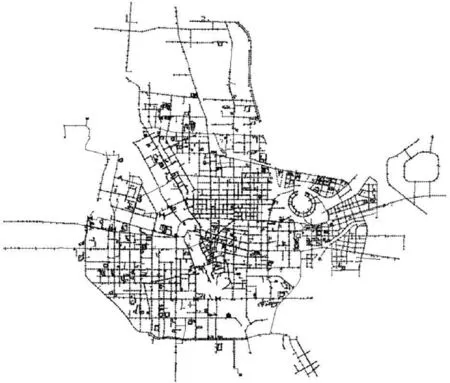
图2 ZZ市供水管网水力模型Fig.2 Hydraulic Model of Water Supply Distribution Network in ZZ City

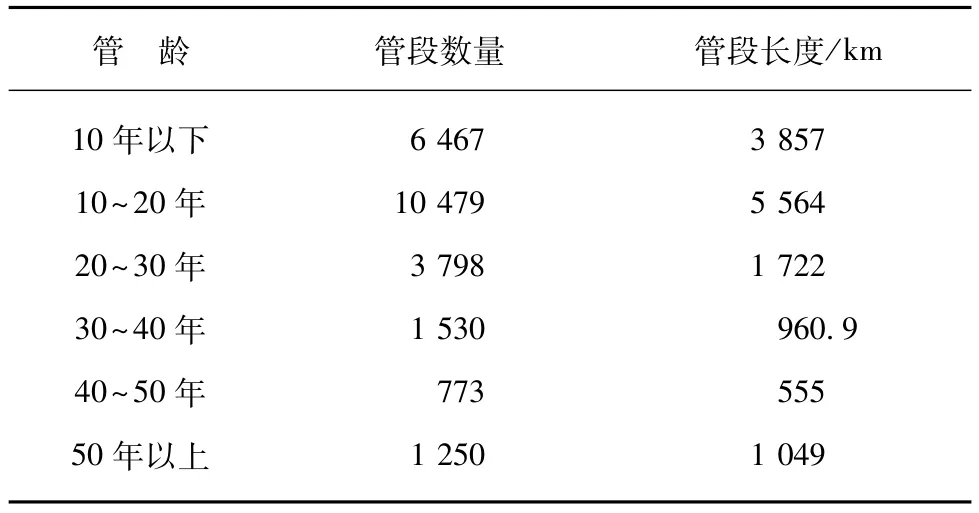
表3 ZZ市供水管网管段信息Tab.3 Pipes Information of Water Supply Distribution Network in ZZ City

该模型现状概况统计如下：

（1）管段数量总数为25 516根；

（2）其中主要管段的管龄集中在10～20年，这个管龄阶段的管段占整个城市中管段长度的比例最高，爆管风险也为最高；

（3）城市中的管材以球墨铸铁、灰口铸铁为主，其他管材还包括PE、镀锌钢管、混凝土管；

（4）模型中模拟了供水管网一天24 h的供水运行状况，其中每15 min为一个时段，总共有96个时段。

4.2 管网数据调用

本文采用matlab对EPANET管网水力模型的数据进行调用，运行一天模型共有96组数据，每组数据包括流速、压力以及压力的变化值。对于某一管段，可根据管段的ID号调出管段的96个时段的流速值。类似地，调取出管段上下游节点的96组压力值，管段每个时段的平均压力为该时段上下游节点压力值的平均值。管段每个时段压力的变化值则为管段该时段的平均压力与其下一时段的平均压力的差值的绝对值。最后，对每组数据进行标准化，即得到了BP神经网络的输入变量。

4.3 BP神经网络评价结果

以管网中编号为567 283的管段为例进行爆管动态风险评估，调取该管段的流速、压力、压力变化值数据。动态风险评价结果如表4所示，评价等级主要集中在良好，或者低危险这两个等级。参考柯庆等［8］的爆管风险评估方法评估该管段的静态爆管风险，并规定静态爆管率低于0.05次／（km·年）则管段属于安全等级，管段的静态爆管率为0.014 9次／（km·年），也是属于安全等级，可以认为，该管段在动态因素影响下也是比较安全的。

表4 爆管动态风险等级评价结果Tab.4 Assessment Results of Dynamic Risk Levels for Pipe Burst

由评价结果可知：

（1）在 0∶00～7∶30 以及 23∶15～24∶00，动态风险评价都为良好等级，这是因为该时段为凌晨，用水量比较小，且用水曲线的变化较为平缓，因此管段流速较低，并且压力变化值也较小，故管段较为安全；

（2）在 7∶30～23∶15，评价等级主要集中在低危险，当中有两段短暂的时段为良好等级，这可能是因为这两个时段在中午和夜晚的用水高峰附近，管段压力较低。

对静态爆管率进行修正后，得到的爆管率-时间曲线如图3所示，该管道的爆管率在某些时刻最高能达到 0.025次／（km·年），低于 0.05次／（km·年），仍在安全范围内，可见该管段经过动态爆管率风险评估之后，安全评级仍然为安全。

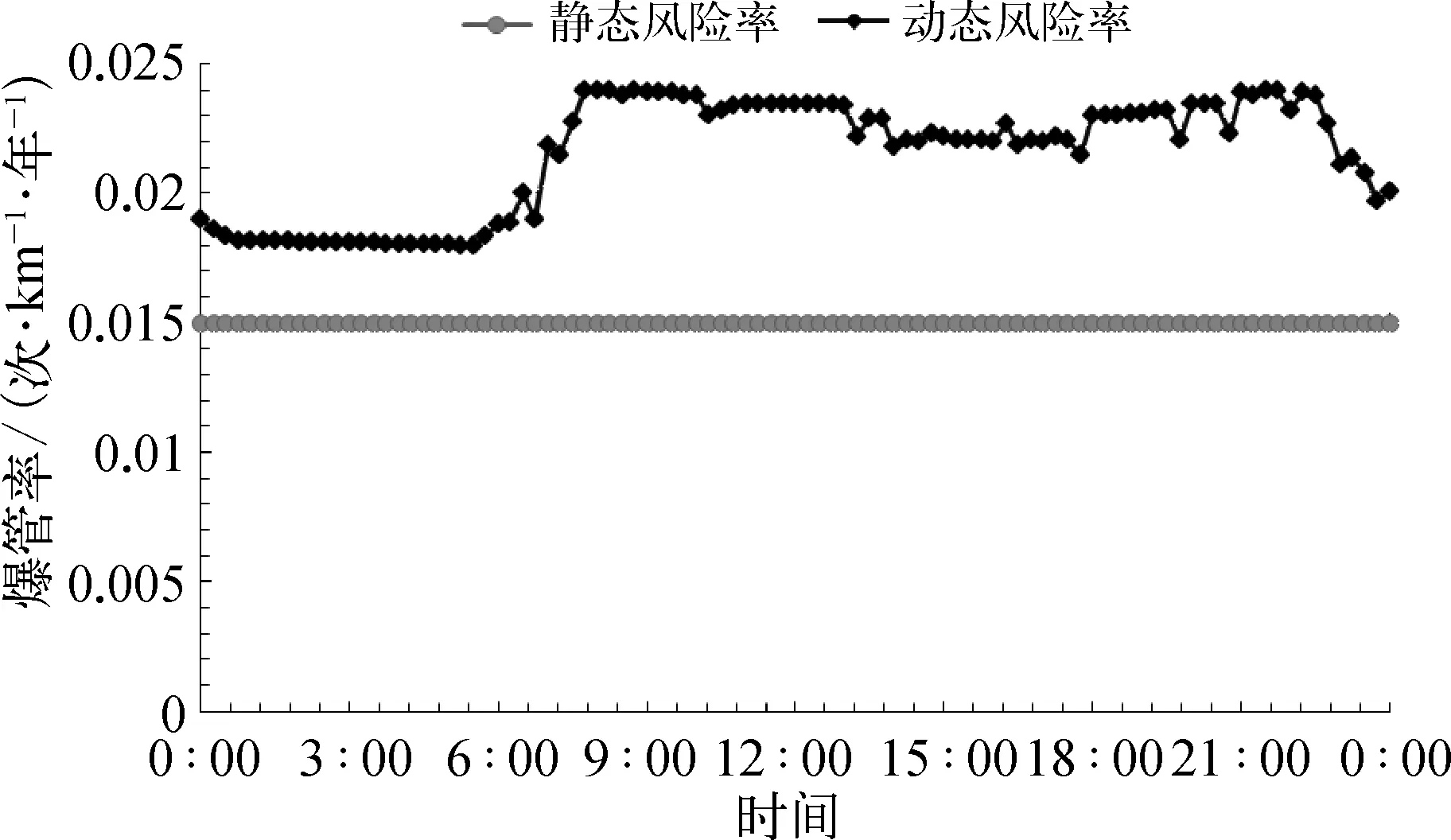
图3 低危险管段动态爆管率曲线Fig.3 Burst Rate-Time Curve for Low Risk Pipes

对管网中另一条静态爆管率为0.033 5次／（km·年）的管段进行动态爆管率评估，由图4可知，在某些时段管段的动态爆管率超过了0.05次／（km·年），甚至达到了0.07次／（km·年），在这些时段，本管段就成为了高危险的管段。可见有关部门需要对此管段进行关注，避免因为此管段的静态爆管率低于0.05次／（km·年）就把它作为安全管段来对待，应更加科学地预防爆管事故的发生。

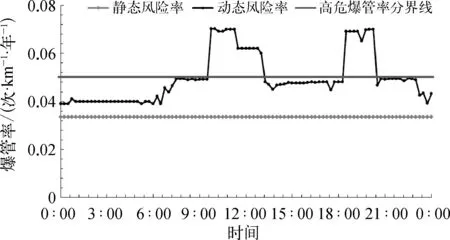
图4 中危险管段动态爆管率曲线Fig.4 Burst Rate-Time Curve for Medium Risk Pipes

5 结果与讨论

本文所提出的供水管网爆管风险评估模型，能够动态地对某一时段内管段的爆管风险进行评估。由于影响管段爆管的水力因素是动态的，因此爆管风险在1 d内也是随时间变化的。然而，以往的研究多着重于预测在一段较长的时间内管段的爆管次数，即在预测的时段内爆管率是一个固定值。而本文的爆管动态风险评估模型则考虑了流速、压力以及压力变化值这三个动态水力因素，能够揭示出管段在一段时间内的实时爆管风险，配合爆管静态风险评估能够更为综合地进行管道安全评价，这是该模型相比于传统模型的主要优势。由ZZ市的实例分析可知，该动态风险评估模型能够暴露出一些看似安全或者危险等级比较低的管段的隐藏危险性，对整个管网的所有管段进行动态风险评估，则能够进一步将潜在的危险管段识别出来，从而针对这些管段，在水力动态和管材维护两个方面加强管道的维护与管理，保障管网供水安全性。

然而，该动态风险评估模型也存在一定的缺陷，其在综合程度以及精度上仍存在不足。该模型过多地依赖于BP神经网络，评估结果存在一定的波动性。其次，模型仅考虑了流速、压力、压力变化值三个动态因素，而忽略了诸如压力瞬变、温度、路面载荷等的影响，尚不能涵盖所有对爆管有重要影响的物理因素。如能对上述的问题做更深入的研究，供水管网爆管动态风险评估模型能够得到进一步的完善。此外，该模型的三个评价指标的数据来自管网水力模型，因此评价结果的准确度与模型精度有关，如将评价结果应用于指导管网改造、管道维护，则需要根据在线仪器的流量、压力数据把水力模型校核到足够高的精度。

［1］何芳，刘遂庆.供水管网爆管事故分析与对策探讨［J］.管道技术与设备，2004（5）：20-23.

［2］Shamir U，Howard C D D.An analytic approach to scheduling pipe replacement［J］.Journal American Water Works Association，1979，71（5）：248-258.

［3］Moglia M，Davis P，Burn S.Strong exploration of a cast iron pipe failure model［J］.Reliability Engineering ＆ System Safety，2008，93（6）：885-896.

［4］Kleiner Y，Rajani B.Comparison of four models to rank failure likelihood of individual pipes ［J］.Journal of Hydroinformatics，2012，14（3）：659.

［5］Scheidegger A，Scholten L，Maurer M，et al.Extension of pipe failure models to consider the absence of data from replaced pipes［J］.Water Research，2013，47（11）：3696-3705.

［6］Gat Y L.Extending the Yule process to model recurrent pipe failures in water supply networks ［J］.Urban Water Journal，2014，11（8）：617-630.

［7］张宏伟，牛志广，陈超，等.供水管道漏损预测模型研究［J］.中国给水排水，2001，17（6）：7-9.

［8］柯庆，周超，王林森，等.供水管网爆管风险评估模型研究［J］.给水排水，2016，42（7）：114-118.