空心稳定杆的优化设计

王伟，王海艳，熊朝恩

（1.一汽技术中心轻型车部底盘设计室，吉林 长春 130011；2.一汽技术中心JC越野车研究所，吉林 长春 130011）

前言

为提高汽车的操作稳定性，同时也可以改善汽车的乘坐舒适性，稳定杆被广泛应用于汽车悬架系统。根据稳定杆在实际工作中的受力特点，可将其设计为空心稳定杆，获得30%～45%的降重效果，因此空心稳定杆成为目前稳定杆领域的研究热点[1]。本文综合考虑各种因素，利用能量法给出空心稳定杆侧倾角刚度、各截面应力计算公式和最大第三强度理论相当应力（以下简称相当应力）的横截面位置，详细介绍了空心稳定杆各设计参数对其性能的影响。最后在保证空心稳定杆设计指标、强度等要求下，以质量最小为目标，以空心稳定杆结构及安装参数为设计变量，建立其优化设计模型，并利用MATLAB软件完成了对空心稳定杆的优化设计。

1 空心稳定杆设计计算

在多数汽车上，空心稳定杆中部的两端自由地支承在两个橡胶套筒内，而套筒则固定在车架上。空心稳定杆两侧纵向部分的末端通过支杆与悬架下摆臂上的弹簧支座相连[3]。在非独立悬架系统中，也有将空心稳定杆中部通过吊臂总成与车架相连，纵向部分的末端通过固定支架与车桥相连。某实际轻型商用车前悬架的空心稳定杆系统就采用了这种连接方式，如图1所示。

图1 某轻型商用车前空心稳定杆系统

对于轻型商用车来说，车轮侧倾角刚度要远大于弹性元件和稳定杆的角刚度，故桥的转角较小；另一方面，桥中部竖直方向变形很小。由于对称性，稳定杆中部相对于桥中部无变形、无转角，于是稳定杆中部可简化为固定端。截取空心稳定杆一半加以讨论，建立其数学模型如图2所示（在此未考虑稳定杆为避免和其他零件干涉而形成的弯曲部分）。

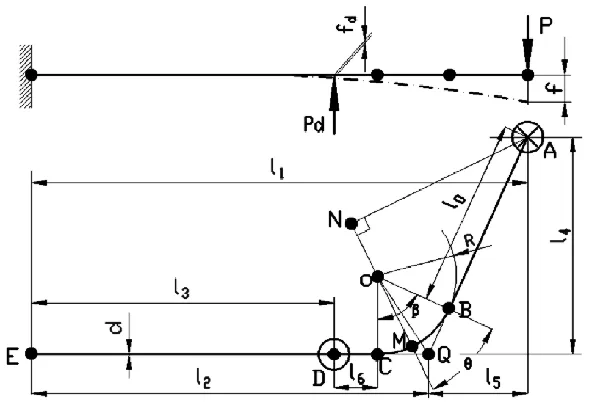
图2 空心稳定杆数学模型

在图2中，A为端点，在该点通过稳定杆吊臂与车身相连，AB段为直线段，BC段为圆弧，D点为稳定杆与吊臂的连接点，中点E为固定端。d、l1、l2、l3、l4、R为稳定杆设计参数，其中l3为稳定杆的安装参数，其他为稳定杆结构参数。

图中部分参数可表示为：l5= l1-l2,

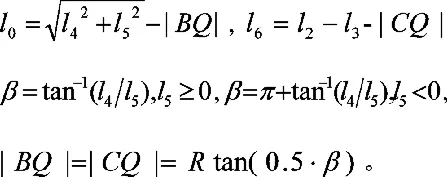
1.1 空心稳定杆侧倾角刚度

AB 段：PAB(x)=P，MAB(x)=P·x，MxAB(x)=0，（0≦x≦l0）；

BC 段：PBC(θ)=P，（0﹤θ≦β）有

CD段：PCD(x)=P，MCD(x)=Px，MxCD(x)=Pl4

DE 段：PDE(x)=P- Pd，当MDE(x)=P(l1- l3)+ (P-Pd)x，MxDE(x)=Pl4；

上式中，PAB、PBC、PCD、PDE依次为各段的剪力；MAB、MBC、MCD、MDE依次为各段的弯矩，MxAB、MxBC、MxCD、MxDE依次为各段的扭矩，根据克拉贝依隆原理[2-3]，有：

取P=1时，对上式整理得：

式中，f为稳定杆端点A处在单位载荷P作用下的垂直位移；E为抗弯刚度；I为截面惯性矩；μ为泊松比。

由公式（1）可得到稳定杆的线刚度为 1/f，则稳定杆的侧倾角刚度可以表示为：

1.2 空心稳定杆应力及危险截面位置

按照图2所示的受力情况，对稳定杆进行应力分析，其各截面所受的最大应力可以表示为：

式中，M、Mx、P分别为各截面的弯矩、扭矩和剪力，W、WP、A分别为各截面处的抗弯截面系数、抗扭截面系数及面积，σ、τ1、τ2为各截面M、Mx、P所产生的最大应力。通过式（3）可以计算出稳定杆各段各截面所受的最大正、切应力。

稳定杆工作时的危险截面有可能在BC段或者D点，对于危险截面有，故可以忽略τ2的影响。下面按照第三强度理论（最大切应力理论）求解稳定杆危险截面位置：

BC段任意点的相当应力为：

由式（4）和式（6）可以确定得到稳定杆危险点位置及其最大相当应力为：

稳定杆的强度条件可以表示为：

式中，σs为材料的屈服极限，ns为许用安全系数。

空心稳定杆质量是稳定杆重要的经济性指标，在此给出稳定杆的质量计算公式为：

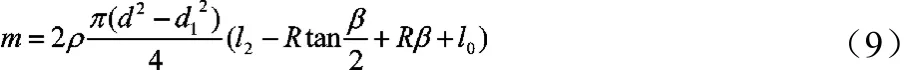
式中，d1为空心稳定杆内径，ρ为密度。

通过上述计算分析，完成了空心稳定杆侧倾角刚度、任意截面最大应力的计算，同时按照第三强度理论给出了空心稳定杆的危险截面位置。

1 设计参数对侧倾角刚度、最大相当应力和质量的影响

已知某一空心稳定杆设计尺寸为：d=36mm，d1=20mm，l1=l2=435mm，l3=340mm，l4=220mm，R=40mm，车身转角φr=5°。依次将d、l1、l2、l3、l4、R作为变量，求解出各变量对侧倾角刚度、最大相当应力和质量的百分比灵敏度为：

图3 各设计参数对稳定杆侧倾角刚度的影响

式中，xi0(i=1,2…,6)为各参数的初始值，△xi为各参数的变化值；ki0、σi0、mi0分别为各参数初始值对应的角刚度、最大相当应力及质量；△xi0、△σi0、△mi0分别为各参数对应的角刚度、最大相当应力和质量的变化值。以各灵敏度的分母、分子分别作为横、纵坐标，绘制图形，结果如图3、图4和图5所示。

图4 各设计参数对稳定杆最大相当应力的影响

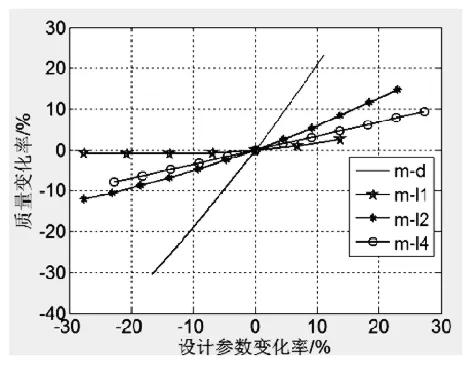
图5 各设计参数对稳定杆质量的影响

从图3可以看出，各设计参数对侧倾角刚度影响从大到小依次为：d、l4、l1、l3、R；从图4可以看出，各设计参数对最大相当应力影响从大到小依次为：l4、l1、d、l2、l3、R；从图5可以看出，l3不影响稳定杆质量，R对稳定杆质量的影响非常小，其余设计参数对质量影响从大到小依次为：d、l2、l4、l1。综合分析上述结果，会发现增大稳定杆直径d可以明显提高侧倾角刚度，但会导致质量增加较多；减小l4也会明显增加侧倾角刚度，也会导致最大相当应力增大明显；l1的取值大小对侧倾角刚度、最大相当应力影响明显；增加l3会使侧倾角刚度增加，最大相当应力减小，同时不会导致质量增加。总之，认知稳定杆各设计参数对其性能的影响，

对合理设计稳定杆具有重要的指导意义。

2 优化设计

关于空心稳定杆的优化设计，首先，要保证与操纵稳定性直接相关的设计指标，即侧倾角刚度；其次，空心稳定杆的设计必须满足强度要求；第三，应尽量减轻空心稳定杆的质量，提高其经济性[4-5]。为此提出稳定杆的优化设计目标：在满足布置空间要求、强度条件、侧倾角刚度期望值的前提下，设计出质量最小的空心稳定杆。

定义空心稳定杆优化设计变量为：

式中，d、l1、l2、l3、l4、R与图2中的稳定杆设计参数相一致。

定义优化设计的目标函数为：

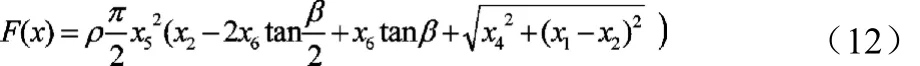
优化设计的约束条件要充分考虑到空心稳定杆的布置空间、刚度、强度、制造工艺及相关零件强度等方面的要求，因此建立下列约束方程为：

（a）为避免空心稳定杆下支架内衬套与稳定杆圆角部分发生干涉，有约束方程：

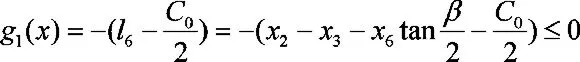
式中，C0为稳定杆下支架孔内衬套长度。

（b）稳定杆端部与吊臂相连，吊臂上端与上支架相连，为了减小上支架所受的弯曲应力，同时避免吊臂与弹性元件干涉，当稳定杆端部在车架外侧时要求稳定杆端部距车架外侧面不能大于C1，有约束方程：

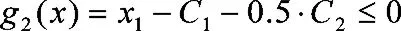
式中，C2为车架外宽，C1为支架悬臂长度，C1越大，则支架应设计得越庞大。

（c）稳定杆支架位于车架内侧时，稳定杆上支架距车架外侧的悬臂不能大于C1′，有约束方程：

式中， C1′为支架在车架内侧时支架悬臂长度。

（d）稳定杆端部打孔，通过连接件与吊臂相连，所以要求端部部分不能为圆弧，必须为直线。有约束方程：

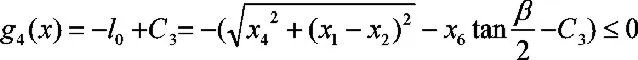
式中，C3为一常数，要求该常数能保证装配时夹具不与稳定杆干涉。

（e）稳定杆原材料为棒料或者管料，在弯曲成型时圆弧外部受拉，内侧受压，为了避免成型时形成较大的内应力，对半径与直径比值提出下限值，有约束方程：

式中，C4为半径与直径之比，一般要求大于1.5。

（f）对于稳定杆侧倾角刚度期望值K及其允许误差Ke，有约束方程：

（g）按照稳定杆的强度要求，最大第三相当应力应小于材料的许用应力，有强度约束方程：

（h）要求图2中衬套安装位置D点受力不能太大，否则会削弱衬套的使用寿命，有约束方程：

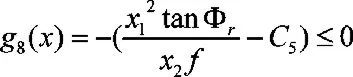
式中， C5为衬套受力限值。

（i）要求所有设计参数都大于0，有：

由以上分析可以看出，空心稳定杆优化设计可以看成是一个6维，9个不等式约束，以质量最小为目标函数的单目标非线性规划问题。

2 利用MATLAB进行优化计算

利用MATLAB软件优化工具箱的fmincon()函数，对优化设计模型进行求解。一共建立3个M文件，分别为目标函数文件、约束函数文件和原本文件。

为了验证算法的可行性，以某商用车前悬架为例，对其空心稳定杆进行优化设计，并与原设计结果进行对比，输入的原始数据如表1所列。

表1 原始数据

将表1中的原始数据输入到由MATLAB软件编写的优化设计程序当中，通过计算分析得出了稳定杆优化结果，原方案与优化结果对比如表2所列。

表2 原方案与优化方案结果对比

对比计算结果发现，在最大相当应力和侧倾角刚度相等时，优化后的方案质量为原方案的84%，稳定杆支撑点D处的受力为原方案的85%，圆角处的曲率半径与直径比由原来的 1.1增大为 2.0。另外，从优化设计结果对应的约束方程g(x)=[-5 0 -150 -28 -23 0 0 -4401]可以看出，约束条件1、2、6、7同时限制了空心稳定杆的质量，为了减轻空心稳定杆质量，还可以考虑：

（a）减小衬套轴向尺寸 C0，但这会增大衬套应力，降低其寿命；

（b）增加稳定杆上支架的悬臂长度 C1，但这会导致稳定杆上支架弯曲应力增大；

（c）减小稳定杆刚度期望值，或者增加刚度允许误差；

（d）增加稳定杆许用应力，比如采用屈服极限更高的材料，或者降低许用安全系数，但前者会增加材料成本，后者会降低稳定杆疲劳寿命。

根据以往的试验经验，除合理的选材和合理的设计空心稳定杆结构以外，其金相组织和表面质量对寿命的影响非常大，因此必须严格控制热处理工艺和表面质量。关于稳定杆重量，采用管材制作的中空稳定杆，较实心来说，在保证性能一致的同时能大幅度降重。

3 结束语

（a）空心稳定杆与整车平顺性和操纵稳定性密切相关，空心稳定杆必须起到合理协调整车垂直刚度和侧倾角刚度的目的。利用能量法实现了对空心稳定杆侧倾角刚度、各截面应力的计算和最大相当应力处危险横截面位置的确定。

（b）利用百分比灵敏度分析了空心稳定杆各设计参数对其侧倾角刚度、最大相当应力和质量的影响，得出在设计选取稳定杆各参数时，必须综合考虑每一个参数对空心稳定杆侧倾角刚度、强度、布置空间、重量的影响。

（c）在满足布置空间、侧倾角刚度期望值、强度、制造工艺等众多条件下，以质量最小为目标，建立了空心稳定杆优化设计模型，用 MATLAB工具箱便捷地完成了空心稳定杆的优化设计，优化后的空心稳定杆在保证性能的前提下，经济性得到提高，加工工艺得到改善，而且有效地提高了稳定杆总成其他零件衬套、支架的使用寿命。

[1] 顾伟清等.空心稳定杆设计及实效分析.技术导向,2017.04

[2] 王望予主编.汽车设计.第4版.北京:机械工业出版社,2004.8.

[3] 聂玉琴,孟广伟主编.材料力学.北京:机械工业出版社,2004.2.

[4] 陈家瑞.汽车构造.第三版.北京:机械工业出版社,2009.2.

[5] 丁能根,张宏兵等.横向稳定杆性能计算及其影响因素分析.汽车技术,2006(1):23～26.