蓄电池等效电路充放电模型参数辨识实验方法研究
彭善涛,盛小明
(1.苏州大学机电工程学院,江苏 苏州 215021;2. 苏州建设交通高等职业技术学校,江苏 苏州 215104)
前言
蓄电池的电压、电流和温度等状态可以通过传感器直接检测得到,但动力蓄电池的荷电状态(State of Charge, SOC)等无法由传感器直接测量,必须通过某种算法间接估计得到,而这些算法都离不开蓄电池的模型及其模型参数。蓄电池等效电路模型及其参数为蓄电池的硬件在环境仿真分析中提供基础,为SOC估计和SOH估计提供依据,为动力蓄电池的管理和控制提供参考。
目前对于动力蓄电池的模型研究主要采用一种新的具有持续相关性的M序列辨识方法,通过基于具有持续相关性的辨识M序列基础上对充放电模型参数辨识实验研究,能够较好的改进Thevenin模型及其模型参数,可以较准确的估计蓄电池SOC。
1 辨识实验设计
实验使用德国生产的digatron动力蓄电池充放电设备。试验对象选取额定安时量为80Ah,标称电压为12.8V,上下截止电压为 10.8—14.7V的铅酸动力蓄电池组。由于温度对铅酸动力蓄电池影响不是很敏感,因此本试验温度环境为室温 25±1ºC。
1.1 实验激励
根据先验知识,我们选择铅酸动力蓄电池的最大工作频率fmax=0.5,铅酸动力蓄电池的过渡过程时间Ts=12s. 根据式(3.2.25)可知,我们可以确定 M 序列激励的相关参数为:M序列周期Np=31;M序列移位寄存器级数p=5;M序列单个脉冲持续时间=NpΔt=15.5s,M 序列输入电流幅值Ia=0.3C=24A,整个激励持续一个周期。
在给M序列逻辑状态“1”和“0”赋值时,设计成:当充电过程中,出现逻辑状态“1”时,输出充电电流24A;在放电过程中,出现逻辑状态“1”时,输出放电电流24A。而当出现逻辑状态“0”时,则不论是铅酸动力蓄电池处于充电过程还是放电过程,都认为是处于静置状态。单个M序列电流激励脉冲如图1所示。

图1 试验用M序列电流激励
1.2 极化时间[62_68]
铅酸动力蓄电池的极化时间常数可以通过脉冲放电方法求得。此方法适合离线估计模型参数的初始值,基本方法是将电池静置较长一段时间后(通常根据试验对象的先验知识确定静置时间),让电池以恒定的电流放电一段时间,并记录下电池的电压响应,然后根据电压和电流计算模型的参数。图2是对试验用铅酸动力蓄电池采用幅值是24A、持续时间为20s横流脉冲放电,脉冲放电结束后在静置60s的电压响应曲线。
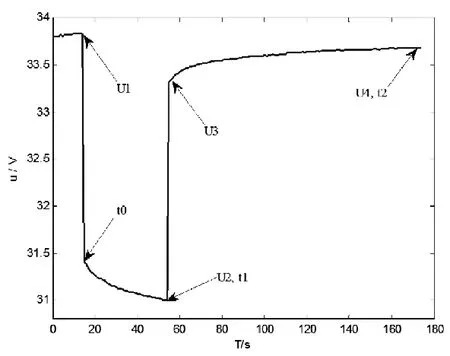
图2 脉冲放电电压响应曲线
电池在脉冲电流放电后,随着静置时间的延长,电容C上的电量会通过阻容回路对R放电而逐步消失,也即两个阻容并联环节上的电压会逐渐归于零。根据电池开路电压的定义,因此可以认为,此时电池两段的端电压即是电池的开路电压。
在观察电压缓慢变化那一段时间,即在t1到t2时间段内,流过电池的电流为零,端电压由于表面电容的作用而近似呈现指数上升。于是系统电路的时间常数可以数学描述为:

2 充电模型参数辨识实验方法
2.1 充电模型实验方法
(1)将试验用的铅酸动力蓄电池完全放电后,静置一个小时;
(2)选取等间隔的SOC点对电池进行试验,试验选取的 SOC 点为 0.9、0.8、······、0.1;
(3)在每一个SOC点使用图1所示单个电流激励脉冲充电。激励脉冲变化规律与M序列一样,单个脉冲持续时间为15.5s;
(4)电池放完电后,再充电到0.1SOC处,静置40min后进行第一个脉冲循环;
(5)结束完单个电流激励脉冲循环后,进行脉冲放电试验,以0.3C横流放电20s后,静置60s,记录如图2所示的电压响应曲线图;
(6)最后再以0.3C恒流充电将电池充电至0.2SOC处,静置40min后进行第二个脉冲循环,依次类推,完成整个试验循环。整个电流激励如图3所示。

图3 全过程充电电流激励原理
2.2 充电模型试验结果
图3所示电流激励下,试验用铅酸动力蓄电池系统的全过程电压输出响应如图4所示。
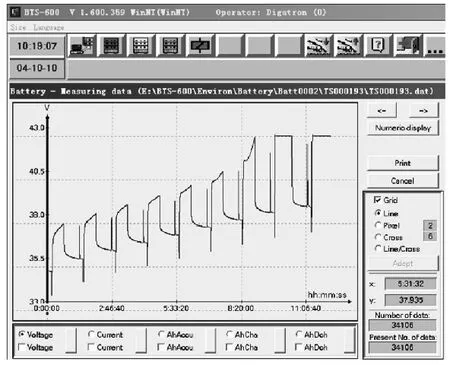
图4 充电过程电压输出响应
从图中,我们可以观察到在第7个循环脉冲周期处,电压上升的曲线较陡,这是由于铅酸蓄电池在充电后期将进入恒压限流阶段。从图中,我们还可以观察到在第8个和第9个循环脉冲周期处,电压变成恒定的,这是由于在给铅酸动力蓄电池充电过程中,当电池电压达到上限标称电压 42.1V时,就转变成恒压充电直至电流减少到1A。由于在SOC=0.8处,电池的电压已经达到 42.1V,所以后面充电过程都是采取恒压限流充电。
2.3 充电模型数据处理
通过试验采集的输入电流和输出电压数据,根据先知的辨识理论依据,用最小二乘一次完成算法辨识出Thevenin模型中的各个参数,辨识结果如下所述。
图5所示为Thevenin模型中串联电阻R1阻值的辨识结果。从图中可以看出,电路中串联电阻R1的阻值,总体趋势随着荷电状态SOC的增加而变大,尤其在充电后期电阻值较大。在充电后期,荷电状态SOC等于0.9时,电阻值产生个突降,主要是因为充电后期RC并联环节电压产生突变,这也解释了为什么充电后期电容C值较小的原因。

图5 电阻R1阻值
图6所示为Thevenin模型中RC模块电阻R阻值的辨识结果。从图中可以看出,RC并联环节中的电阻R的阻值,随着荷电状态SOC的增加而增大,也就是说,VRLA蓄电池充电效率随着 SOC的增加而降低。随着充电时间的增加,RC并联环节上电压在不断升高,从而导致电阻R的阻值呈现增大的趋势。

图6 电阻R阻值
图7所示为Thevenin模型中RC模块电容C值的辨识结果。从图中可以看出,RC并联环节中的电容C值,随着荷电状态SOC的增加而减小。随着充电时间的增加,RC并联环节上电压在不断升高,双电层电容上的电压降不断增加,而流经电容上的电量Q虽然也在增加,但是总体变化量低于电压,根据电容计算公式C=Q/U可以得到电容C值随着荷电状态SOC呈现减小的趋势。

图7 电容C值
图8所示为Thevenin模型中开路电压的辨识结果与试验记录开路电压对比图。从图中可以看出,最小二乘一次算法辨识得到的电池各个 SOC点的开路电压与电池实验所测得到的开路电压基本吻合。在处的出现的电压奇异点(辨识计算所得的开路电压与电池实验测得到的开路电压差距较之其它SOC处的大),这是由于在SOC=0.8时,电池充电正好处在恒流限压充电和恒压限流充电交换的阶段,在电流迅速降低的阶段,电池达到SOC=0.8的安时数,但实际上此刻电池处于浮充阶段,因此静置后所得的数据都略微偏小。

图8 开路电压对比图
3 放电模型参数辨识实验方法
3.1 放电模型实验方法
(1)将试验用的铅酸动力蓄电池充满电后,静置一个小时;
(2)选取等间隔的SOC点对电池进行试验,试验选取的 SOC 点为 0.9、0.8、······、0.1;
(3)在每一个SOC点使用如图4.9所示的单个电流激励脉冲充电。激励脉冲变化规律与M序列一样,单个脉冲持续时间为15.5s;
(4)电池满电状态下放电至0.9SOC处,静置40min后进行第一个脉冲循环;
(5)结束完单个电流激励脉冲循环后,再进行脉冲放电试验,以0.3C恒流放电20s后,静置60s,记录如图4.2所示的电压响应曲线图;
(6)最后再以0.3C恒流放电将电池放电至0.8SOC处,静置40min后进行第二个脉冲循环,依次类推,完成整个试验循环。整个电流激励如图9所示。

图9 单个放电电流激励脉冲原理
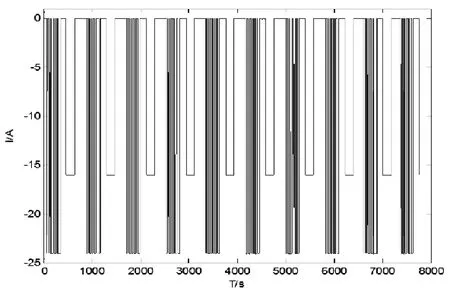
图10 全过程放电电流激励原理
3.2 放电模型试验结果
图10所示电流激励下,试验用铅酸动力蓄电池系统的全过程电压输出响应如图11所示。
从图中,我们可以观察到,放电过程中给定图8所示的电流激励下,电池的电压输出基本较稳定。在第9个循环脉冲周期处,电压下降曲线出现很陡的一段,分析其原因是由于电池放电后期,电池电阻急剧变小,导致电压下降迅速。

图11 放电过程电压输出响应
3.3 放电模型数据处理
通过试验采集的输入电流和输出电压数据,根据先知的辨识理论依据,使用最小二乘一次完成算法辨识出Thevenin模型中的各个参数,辨识结果如下所述。
图12所示为Thevenin模型中串联电阻R1阻值的辨识结果。从图中可以看出,电路中串联电阻R1的阻值,随着荷电状态SOC的增加而减小,也就是说随着放电深度DOD的增加而增大,在DOD接近零时,辨识出来的电阻R1偏大。这是由于RC并联环节的电压在电池放电初期由于电容具有容性性质,所以电压降低存在一个滞后期,从而导致串联电阻R1上的电压偏大造成的。从化学角度来考虑,VRLA蓄电池随着放电深度 DOD的加深、电解液泄漏的恶化、单向节流阀开启次数增多等而失水量增多等因素影响下,隔膜内阻会明显增大。同时,在放电过程正极板上多孔隙二氧化铅、负极板上海绵状铅分别在与硫酸溶液接触的表面上形成硫酸铅,其导电性比活性物质导电性差,加上电解液浓度不断降低,所以电池的欧姆内阻增加。

图12 电阻R1阻值
图13所示为Thevenin模型中RC模块中电阻R阻值的辨识结果。从图中可以看出,电路中并联电阻R的阻值,随着荷电状态SOC的增加而增大,也就是说随着放电深度DOD的增加而减小。在电池放电初期,电阻R较大的原因是由于当电池通过电流放电时,欧姆电阻压降在瞬间产生,而双层电容上的电压降,需要经历放电而较迟产生,因此实时采集的电压数据偏大,导致内阻R偏大。

图13 电阻R阻值
图14所示为Thevenin模型中RC模块中电容C值的辨识结果。从图中可以看出,RC并联环节中的电容C随着荷电状态SOC的增加而减小,随着放电深度DOD的增加而增加。根据电容计算公式C=Q/U,随着放电深度的不断增加,电压U不断减小,流过电容上的电量Q也在减小,但是相对电压减小量要小,因此电容C总体趋势在不断增加。

图14 电阻C阻值
图15所示为Thevenin模型中开路电压的辨识结果与试验记录开路电压对比图。从图中可以看出,采用最小二乘法辨识出来的电池开路电压与实际实验中所测得的电池开路电压曲线较吻合。
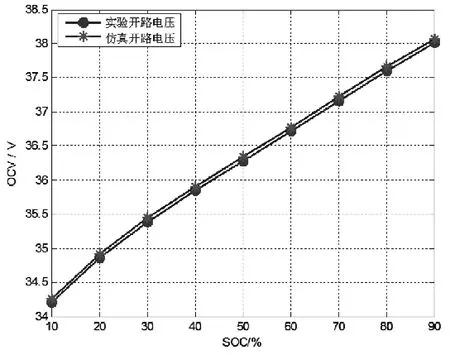
图15 开路电压对比图
4 结论
由于铅酸动力蓄电池在充放电过程内部参数变化情况并不一致,如果单纯的以放电过程数据辨识建立的蓄电池等效电路模型,建立的模型在描述蓄电池性能上存在的误差较大。通过基于具有持续相关性的辨识 M 序列基础上对充放电模型参数辨识实验研究,对选用的Thevenin模型采取改进并进行建模仿真,发现可以较准确的表现出蓄电池的工作特性。
综上所述,通过对充放电模型参数辨识实验方法的研究可以有效帮助改进Thevenin模型,使其能够更加准确的描述出蓄电池系统的工作特性,更加适合用于电动汽车动力蓄电池等效电路模型的相关仿真研究。
[1] 陈金干.基于模型的动力电池参数估计研究[J].电动汽车, 2009:1-4.
[2] 杨浩.模型与算法[M].北京:北方交通大学出版社,2002.
[3] 冯培悌.系统辨识[M]. 杭州: 浙江大学出版社,2004.
[4] 侯媛彬,汪梅.系统辨识及其 MATLAB 仿真[M].北京:科学出版社,2004.
[5] 王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社,2004.
[6] 林成涛,陈全世等.电动汽车电池功率输入等效电路模型的比较研究[J].清华大学学报(自然科学版),2006 28(3):229-235.

