转角不对中转子系统的电机电流特性
郭伟杰 ,杨兆建 ,石江波 ,李 峰
(1.太原理工大学 机械工程学院,山西 太原 030024;2.煤矿综采装备山西省重点实验室,山西 太原 030024)
1 引言
转子系统是旋转机械的核心部件,而不对中是最为常见的故障之一,约占总故障的60%[1],具有转子不对中的系统在运行过程中易出现轴挠曲变形、机械振动、轴承早期磨损及油膜失稳等现象[2],因此国内外学者关于转子系统不平行故障的研究有很多。
转子系统不对中故障可以分为平行不对中、转角不对中和平行转角不对中三种,而在实际工况中,一般二者兼而有之,或者以某种不对中故障为主出现。文献[3]基于谐波平衡法分析了转角不对中故障转子系统的动力学模型,结果表明,系统不仅会产生与不平衡类似的工频振动,而且也会产生工频与转子不对中角方向振动频率倍数的组合频率;文献[4]建立了考虑电机联轴器影响的双盘不对中-碰摩耦合故障转子系统力学模型和有限元模型,研究了碰摩刚度和不对中角度两个重要参数对系统动力学特性的影响。文献[5]通过对不对中转子系统动力学响应的研究发现,平行不对中故障会激发出较强的一倍谐波分量,而高倍频谐波较弱,而偏角不对中会激发出很强的三次谐波分量;文献[6]建立了一个多跨转子—轴承系统试验台,重点分析了平行不对中和交角不对中转子的动力学特性和振动机理;文献[7]使用等效不对中力矩和接触理论研究了不同转速下转角不对中故障的转子系统的动力学特性,并认为二倍频比例值可作为含有不对中故障转子系统故障严重程度的一个判断依据。从以往的研究文献中可以看出,大部分的文献都是通过振动分析方法来研究转子系统的不对中故障,而将电流分析方法(MSCA)应用到转子系统的平行不对中故障的研究相对较少,而电流分析方法相对于振动分析方法具有信息集成度高、传递路径短、信噪比高等优点[8]。
针对转子系统转角不对中故障,建立转子系统动力学模型,推导出转子系统的不对中力矩,并以电机的电磁扭矩为纽带,在MATLAB/Simulink中建立转子系统机电耦合仿真模型,对电机电流信号进行频域分析,研究转子系统在转角不对中故障激励下电机电流信号的耦合特性。
2 机电耦合模型
2.1 转角不对中转子系统动力学模型
单跨转角不对中转子系统示意图,如图1所示。假设将转子系统简化为质量分别为m1的单圆盘与弯扭柔性的无质量轴,并且转轴各向同性,轴承为刚性支撑。转子系统存在微小角不对中量α。转角不对中力矩模型,如图2所示。设电机的输出扭矩为T,则由于转角不对中故障的存在,则扭矩T可以分解为TS和Tz两部分,TS和Tz分别为:


图1 转角不对中转子系统示意图Fig.1 Sketch of Rotor Systems with Angular Misalignment

图2 转角不对中力矩模型Fig.2 Moment Model of Angular Misalignment
由于负载转矩的波动直接影响着气隙扭矩,气隙扭矩的变化通过定子磁通引起定子电流的变化[9],因此我们只考虑绕Z轴的转动,则:

式中:J—转子系统的极转动惯量,J=0.05kg·m2;φr—转子的旋转
角度,φr=ωrt+θr;θr—转子的扭振角位移。
对于转角不对中的转子系统,利用欧拉公式可得其电机的转动角速度与转子系统的角速度将满足下式的关系[10]:

式中:ωr—转子的角速度,ωr=φ˙r;ωm—电机的角速度,ωm=φ˙m;φm
—电机的转角,φm=ωmt+θm;θm—电机轴的扭振角。
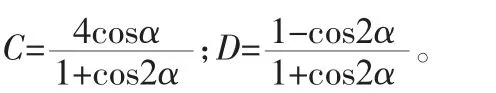
将式(4)对时间进行求导可得:
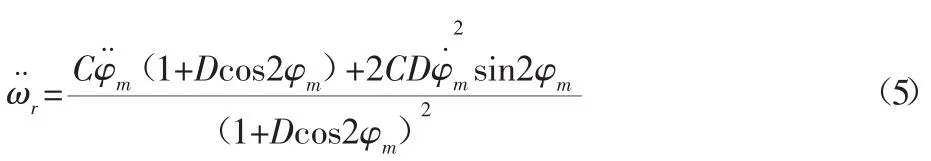
将式(5)代入式(3),得到转子系统的不对中力矩为:

2.2 电机动力学模型
建立三相异步电机在αβo系统下的仿真模型,在αβo系统下电机的电压方程为:
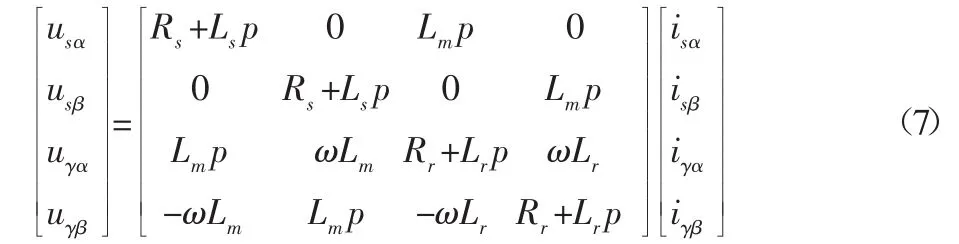
磁链方程:

式中:ωm—电机转动角速度;RS—定子绕组电阻;Rr—转子绕组电阻;LS—定子绕组自感;Lr—转子绕组自感;Lm—定转子绕组互感;np—电极对数;Te—电磁转矩;Mz—惯性扭矩与外扭矩之和;J0—电机的转动惯量。
电机仿真参数如下:f=50Hz;RS=4.26Ω;Rr=3.24Ω;LS=0.666H;Lr=0.670H;Lm=0.651H;U=380V;J0=0.05kg·m2。根据式(6)~式(10)建立三项异步电动机—偏角不对中转子系统的机电耦合仿真模型。
电磁转矩方程:

运动方程:

3 机电耦合模型仿真分析
分别取转子系统的转速为750r/min、1500r/min、3000r/min,每个转速下分别取转角不对中量α为0°、1°、3°和6°,其电磁扭矩和电机电流的频谱图,如图3所示。由图可知,在α为0°时,电磁扭矩会激发出工频偶数倍频的谐波分量,而电流信号会激发出工频奇数倍频的谐波分量,当转子系统存在转角不对中后,电磁扭矩的2倍频分量(100Hz)出现明显的突变,而电流信号的3倍频分量(150Hz)的峰值也出现增大的现象,并且随着α的增大,其幅值也都明显的增大。随着转子系统转速的提高,电磁扭矩和电机电流的高倍频谐波分量逐渐会被淹没,而电磁扭矩的2倍频分量和电流信号的3倍频分量则更为明显,因此可以将其作为转子系统转角不对中故障的一个判断依据。
电磁扭矩的2倍频峰值,如图4所示。由图可知,当转角为0°时,电磁扭矩的二倍频峰值随着转速的增大而变大,但是当转子系统存在转角不对中后,同一转角不对中量下,转速低的二倍频峰值反而比较大;同一转速下,峰值会随着转角不对中量的增大而增大。
电机电流信号的3倍频峰值随转角不对中量的变化规律,如图5所示。由图可知,转速为750r/min和1500r/min时,峰值变化基本相似,但是当转速为更高为3000r/min时,在转角0°<α<2°时,其峰值明显比低转速的高,但是当偏角不对中量继续增大后,其峰值基本与低转速的重合,即电机电流的3倍频分量对转子系统的转角不对中量比较敏感,而对转速并不太敏感。

图3 不同转速下电磁扭矩和电机电流频谱图Fig.3 Frequency Spectrograms of Electromagnetic Torque and Current Signal at Different Speed
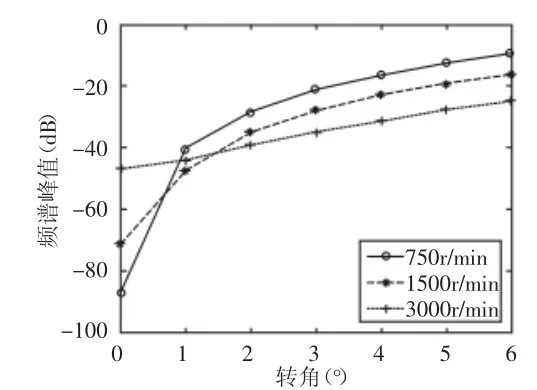
图4 电磁扭矩的二倍频峰值随转角不对中量的变化曲线图Fig.4 Double Frequency Peak Graphs of Electromagnetic Torque with Change of Misaligned Angle
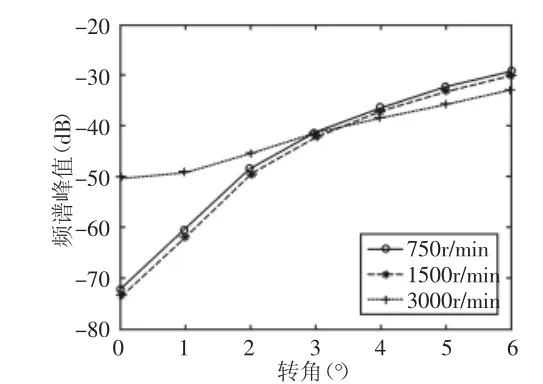
图5 电机电流的三倍频峰值随转角不对中量的变化曲线图Fig.5 Three Frequency Peak Graphs of Motor Current with Change of Misaligned Angle
4 结论
通过建立转角不对中转子系统动力学模型,推导出转角不对中力矩,然后以转角不对中力矩和电机的电磁扭矩为纽带,建立机电耦合仿真模型,并对得到的电磁扭矩信号和电机电流信号进行频谱分析,得到以下结论:
(1)当转子系统不存在转角不对中故障的情况下,电磁扭矩会出现工频的偶数倍频的谐波分量,而电机电流信号会出现奇数倍频的谐波分量。
(2)若转子系统存在转角不对中故障,则电磁扭矩的2倍频谐波分量和电机电流的3倍频谐波分量会出现突变,而且其峰值会随着转角不对中量的增大而增大。
(3)通过不同转速下的对比分析可得,电磁扭矩的2倍频分量和电机电流信号的3倍频分量对转子系统的转角不对中故障更为敏感,而对转速并不敏感,因此其可以作为转角不对中故障的一个判断依据。
[1]赵营豪,陈宏,朱朝鹏.转子不对中定量研究[J].机械设计与制造,2013(12):109-110.(Zhao Ying-hao,Chen Hong,Zhu Chao-peng.Research on the quantitative of misalignment[J].Machinery Design&Manufacture,2013(12):109-110.)
[2]夏松波,张新江,刘占生.旋转机械不对中故障研究综述[J].振动、测试与诊断,1998(3):157-161.(Xia Song-bo,Zhang Xin-jiang,Liu Zhan-sheng.Survey of the research on coupling with misalignment of rotary machinery[J].Journal of Vibration,Measurement&Diagnosis,1998(3):157-161.)
[3]李明.转角不对中故障的转子系统非线性动力学特征[J].振动、测试与诊断,2011,31(5):552-556.(Li Ming.Nonlinear dynamics characteristics of rotor system with angular misalignment[J].Journal of Vibration,Measurement&Diagnosis,2011,31(5):552-556.)
[4]刘杨,太兴宇,姚红良.双盘转子轴承系统不对中-碰摩耦合故障分析[J].振动、测试与诊断,2013,33(5):819-823.(Liu Yang,Tai Xing-yu,Yao Hong-liang.Study on misalignment-rubbing coupling fault of dual-disk rotor-bearing system including the impact of motor coupling[J].Journal of Vibration,Measurement&Diagnosis,2013,33(5):819-823.)
[5]Patel T H,Darpe A K.Vibration response of misaligned rotors[J].Journal of Sound and Vibration,2009,325(3):609-628.
[6]李明,李自刚.联轴器不对中故障转子系统的动力学试验[J].振动、测试与诊断,2015,35(2):345-351.(Li Ming,Li Zi-gang.Theoretical and experimental study on dynamics of rotor-bearing system with the faults of coupling misalignment[J].Journal of Vibration,Measurement&Diagnosis,2015,35(2):345-351.)
[7]刘杨,太兴宇,赵倩.转子系统不对中-碰摩耦合故障的动力学特性[J].东北大学学报:自然科学版,2013,34(4):564-568.(Liu Yang,Tai Xing-yu,Zhao Qing.Dynamics characteristics of misalignment-rubbing coupling fault for rotor system[J].Journal of Northeastern University:Natural Science,2013,34(4):564-568.)
[8]张克南,陆扬,谢里阳.基于SVD方法的弱故障特征提取方法[J].机床与液压,2006(10):214-216.(Zhang Ke-nan,Lu Yang,Xie Li-yang.A New method for extracting the weak fault symptoms of current signal via SVD[J].Machine Tool&Hydraulics,2006(10):214-216.)
[9]张克南,陈一军,谢里阳.电机电流分析法在机床类设备诊断中的应用研究[J].机床与液压,2007,35(3):196-198.(Zhang Ke-nan,Chen Yi-jun,Xie Li-yang.Application of motor current signal analysis in fault diagnosis of machine tools[J].Machine Tool&Hydraulics,2007,35(3):196-198.)
[10]黄锡恺,郑文维.机械原理[M].北京:高等教育出版社,1989:157-216.(Huang Xi-kai,Zheng Wen-wei.Mechanical Principle[M].Beijing:Higher Education Press,1989:157-216.)

